| Autor |
Nachricht |
Pfirsichmensch
Anmeldungsdatum: 09.08.2014
Beiträge: 284
|
 Pfirsichmensch Verfasst am: 27. Nov 2014 10:35 Titel: Kondensator an Stromquelle Pfirsichmensch Verfasst am: 27. Nov 2014 10:35 Titel: Kondensator an Stromquelle |
 |
|
Folgende Aufgabe zur Konstantstromaufladung:
1)
Ein Kondensator dessen Restleitfähigkeit vernachlässigt sei, wird an eine ideale Stromquelle angeschlossen und 20 Sekunden lang mit dem Quellenstrom aufgeladen.
Stellen Sie die folgenden zeitlichen Verläufe dar:
q=f(t) , W=f(t), uc=f(t)
C = 2 Mikrofarad
Iq = 8 Mikroampere
2)
Nun befindet sich parallel zum Kondensator (ungeladen) ein Widerstand Rp=1 kOhm. Ermitteln Sie den zeitlichen Verlauf uc=f(t).
Danach kommt noch eine Aufgabe, aber die lass ich erstmal weg 
Also mein Ansatz für 1)
Da ein konstanter Strom eingespeist wird, geht die Gleichung über in:


=4\frac{V}{s} \cdot t )
Wenn die Aufladung 20 Sekunden erfolgt dann lädt der Kondensator sich auf eine Spannung von 80 V auf.
 = I \cdot t \rightarrow q = 8 \mu A \cdot t )
Nach 20 Sekunden, speichert der Kondensator eine Ladung von 160 mikroCoulomb.
Für die Energie ergeben sich maximal 6,4 mJ. Die Zeitachse kann ich darunter abtragen.
Mein eigentliches Problem kommt jetzt erst:
Anscheinend scheint die Spannung linear anzuwachsen, wenn kein Parallelwiderstand vorhanden ist. Was passiert denn, wenn parallel zum Kondensator noch ein Widerstand vorhanden ist?

Es müsste sich doch eigentlich genau die gleiche Kennlinie ergeben, wie bei einer Aufladung mit Vorwiderstand durch eine Spannungsquelle.
Ich hab doch eine konstante Einströmung. Bei einer idealen Stromquelle, kann die Last alle Spannungswerte annehmen, theoretisch bis ins Unendliche, da kein Widerstand vorhanden ist, der den Stromfluss hemmen kann. Dann MUSS doch der Parallelwiderstand hier verantwortlich für die Spannung sein, auf die sich der Kondensator aufladen wird, ist das richtig?
|
|
 |
Physikaufgabe
Gast
|
 Physikaufgabe Verfasst am: 27. Nov 2014 11:34 Titel: Re: Kondensator an Stromquelle Physikaufgabe Verfasst am: 27. Nov 2014 11:34 Titel: Re: Kondensator an Stromquelle |
 |
|
Hallo,
| Pfirsichmensch hat Folgendes geschrieben: | Folgende Aufgabe zur Konstantstromaufladung:
Es müsste sich doch eigentlich genau die gleiche Kennlinie ergeben, wie bei einer Aufladung mit Vorwiderstand durch eine Spannungsquelle.
|
ja, das ist genau richtig!
Du kannst den parallelen Widerstand des Kondensators als Innenwiderstand der Stromquelle auffassen. Wenn Du jetzt die Stromquelle (mit ihrem Innenwiderstand) in eine zugehörige Spannungsquelle umwandelst, siehst Du, dass Du richtig liegst.
Viele Grüße
Michael
|
|
 |
isi1
Anmeldungsdatum: 03.09.2006
Beiträge: 2902
Wohnort: München
|
 isi1 Verfasst am: 27. Nov 2014 11:44 Titel: Re: Kondensator an Stromquelle isi1 Verfasst am: 27. Nov 2014 11:44 Titel: Re: Kondensator an Stromquelle |
 |
|
| Pfirsichmensch hat Folgendes geschrieben: | | Es müsste sich doch eigentlich genau die gleiche Kennlinie ergeben, wie bei einer Aufladung mit Vorwiderstand durch eine Spannungsquelle. |
Ja, Pfirsich, stimmt,
denn die Stromquelle mit ||-Widerstand R ist äquivalent zur Spannungsqelle mit Uo = i * R dem gleichen (Serien-)Widerstand R.
Ahh, Michael war schneller. 
_________________
Grüße aus München, isi •≡≈ ¹₁₂½√∠∞±∫αβγδεηκλπρσφω ΔΣΦΩ |
|
 |
Pfirsichmensch
Anmeldungsdatum: 09.08.2014
Beiträge: 284
|
|
 |
isi1
Anmeldungsdatum: 03.09.2006
Beiträge: 2902
Wohnort: München
|
 isi1 Verfasst am: 27. Nov 2014 12:21 Titel: isi1 Verfasst am: 27. Nov 2014 12:21 Titel: |
 |
|
Dann kannst umwandeln in eine Stromquelle mit Ri=0 und I = unendlich, Pfirsich,
es ist also keine Stromquelle wie oben diskutiert.
_________________
Grüße aus München, isi •≡≈ ¹₁₂½√∠∞±∫αβγδεηκλπρσφω ΔΣΦΩ |
|
 |
Pfirsichmensch
Anmeldungsdatum: 09.08.2014
Beiträge: 284
|
 Pfirsichmensch Verfasst am: 27. Nov 2014 12:42 Titel: Pfirsichmensch Verfasst am: 27. Nov 2014 12:42 Titel: |
 |
|
|
Ich versteh aber nicht, wie die Stromkennlinie dann in diesem Fall aussieht.
|
|
 |
isi1
Anmeldungsdatum: 03.09.2006
Beiträge: 2902
Wohnort: München
|
 isi1 Verfasst am: 27. Nov 2014 12:45 Titel: isi1 Verfasst am: 27. Nov 2014 12:45 Titel: |
 |
|
| Pfirsichmensch hat Folgendes geschrieben: | | Ich versteh aber nicht, wie die Stromkennlinie dann in diesem Fall aussieht. |
Na einfach einen Diracstoß.
_________________
Grüße aus München, isi •≡≈ ¹₁₂½√∠∞±∫αβγδεηκλπρσφω ΔΣΦΩ |
|
 |
Pfirsichmensch
Anmeldungsdatum: 09.08.2014
Beiträge: 284
|
|
 |
isi1
Anmeldungsdatum: 03.09.2006
Beiträge: 2902
Wohnort: München
|
 isi1 Verfasst am: 27. Nov 2014 15:48 Titel: isi1 Verfasst am: 27. Nov 2014 15:48 Titel: |
 |
|
| Pfirsichmensch hat Folgendes geschrieben: | | Hab ich nun alles verstanden? |
Sehr gur, Pfirsich, erster Preis!
_________________
Grüße aus München, isi •≡≈ ¹₁₂½√∠∞±∫αβγδεηκλπρσφω ΔΣΦΩ |
|
 |
|


















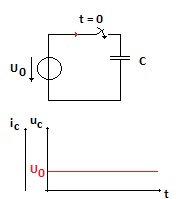
 . Die Spannung am Kondensator beträgt direkt nach Schließen des Schalters Uc = U0. (In der unteren Zeichnung steht Iq, das soll natürlich Ic sein)
. Die Spannung am Kondensator beträgt direkt nach Schließen des Schalters Uc = U0. (In der unteren Zeichnung steht Iq, das soll natürlich Ic sein)