| Autor |
Nachricht |
escapado
Anmeldungsdatum: 08.05.2013
Beiträge: 49
|
 escapado Verfasst am: 22. Jun 2014 11:53 Titel: Zwei-Niveau-System escapado Verfasst am: 22. Jun 2014 11:53 Titel: Zwei-Niveau-System |
 |
|
Hallo ich hänge an folgender Aufgabe fest:
Gegeben sei ein physikalisches System, dessen zweidimensionaler Zustandsraum von den Basisvektoren 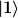 und und 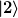 aufgespannt wird, die Energieeigenzustände des Hamiltonoperators aufgespannt wird, die Energieeigenzustände des Hamiltonoperators sind, d.h. sind, d.h.

Das System wird nun in ein Feld gebracht, welches einen Zusatzterm  im Hamiltonoperator zur Folge hat: im Hamiltonoperator zur Folge hat:

a) Lösen Sie das Eigenwertproblem von H. Berechnen Sie die beiden möglichen Eigenwerte  und und  als Funktion der Feldstärke als Funktion der Feldstärke  und drücken Sie die Eigenzustände und drücken Sie die Eigenzustände  und und  von H als Linearkombination der als normiert vorausgestzen Zustände von H als Linearkombination der als normiert vorausgestzen Zustände 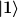 und und  aus. aus.
Meine bisherigen Ideen:
Ein allgemeiner Zustand kann als Linearkombination der Zustände 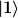 und und  geschrieben werden. Also geschrieben werden. Also
 in Basis in Basis
Ich schreibe jetzt den Hamiltonoperator als Matrix hin:

Die Eigenwertgleichung lautet jetzt doch:

Ist das soweit richtig?
Die Eigenwerte davon sind nämlich relativ hässlich:
 -\sqrt{(-E_1-E_2-(V_{11}-V_{22})\lambda)^2-4(E_1E_2+E_2V_{11}\lambda+E_1V_{22}\lambda -V_{12}V_{21}\lambda^2+V_{11}V_{22}\lambda^2)}\\
<br />
E_{II}= \frac{1}{2}E_1+E_2+\lambda (V_{11}+V_{22}) +\sqrt{(-E_1-E_2-(V_{11}-V_{22})\lambda)^2-4(E_1E_2+E_2V_{11}\lambda+E_1V_{22}\lambda-V_{12}V_{21}\lambda^2+V_{11}V_{22}\lambda^2)})
Ab jetzt hänge ich. Mir ist leider nicht ganz klar, wie ich das vereinfachen könnte und leider weiß ich auch nicht so genau wie ich die neuen Eigenzustände richtig bestimmen kann.
Wäre für etwas Hilfe sehr dankbar  |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8583
|
|
 |
escapado
Anmeldungsdatum: 08.05.2013
Beiträge: 49
|
 escapado Verfasst am: 22. Jun 2014 12:34 Titel: escapado Verfasst am: 22. Jun 2014 12:34 Titel: |
 |
|
Danke für den Tipp.
Dann erhalte ich erst einmal:
-\sqrt{(-tr(H))^2-4\det(H)}\right)\\
<br />
E_{II} = \frac{1}{2}\left( tr(H)+\sqrt{(-tr(H))^2-4\det(H)}\right))
Ich könnte die 1/2 noch hineinmultiplizieren, aber das ändert ja nichts großartig.
Wenn ich der Seite jetzt folge, dann erhalte ich als Eigenvektoren ja
für die drei Fälle:


und für b=c=0 dann (1,0),(0,1).
Aber irgendwie ist mir das noch nicht ganz klar, wie ich nun die Eigenvektoren als Linearkombinationen von 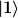 und und  ausdrücken kann. Also für den dritten Fall wären die Eigenfunktionen dieselben wie zuvor. ausdrücken kann. Also für den dritten Fall wären die Eigenfunktionen dieselben wie zuvor.
Aber in den anderen Fällen sehe ich das so nicht. |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8583
|
 jh8979 Verfasst am: 22. Jun 2014 12:46 Titel: jh8979 Verfasst am: 22. Jun 2014 12:46 Titel: |
 |
|
Zuersteinmal kannst Du ja nachprüfen dass es wirklich Eigenvektoren zu den entsprechenden Eigenwerten sind (hab ich nicht, ist vermutlich nicht schwer, aber bisschen Fummelarbeit).
Und als Linearkombinaton von |1>, |2> überleg die mal was es heisst wenn Du einen Vektor  hast. hast. |
|
 |
escapado
Anmeldungsdatum: 08.05.2013
Beiträge: 49
|
 escapado Verfasst am: 24. Jun 2014 15:08 Titel: escapado Verfasst am: 24. Jun 2014 15:08 Titel: |
 |
|
Also so wie ich es aufgeschrieben habe sind die eigenvektoren jeweils so schon linearkombinationen weil ich als basis ja |1> und |2> gewählt habe. Damit ist jeweils der erste Eintrag in dem Vektor der Koeffizient des Basisvektors |1> und der zweite Eintrag entsprechend der Koeffizient des Basisvektors |2>. Damit habe ich das also fertig.
Die sind aber jetzt noch nicht zwingend normiert oder?
Anschließend soll ich annehmen, dass ist und für kleine lambda dann die Energieeigenwerte entwickeln. ist und für kleine lambda dann die Energieeigenwerte entwickeln.
Wenn ich erst einmal die beiden Terme null setze, dann erhalte ich:
^2 \lambda^2 -4(E_1 E_2 -V_{12}V_{21}\lambda^2)}}{2})
Ich bin mir jetzt leider nicht ganz sicher wie ich das entwickeln soll? Soll ich einer Taylorreihe um lambda = 0 darstellen?
Wolframalpha gibt mir dann (siehe unten bei Series expansion at lambda = 0 )
http://www.wolframalpha.com/input/?i=%28E_1+%2B+E_2%29%2F2+%2B+Sqrt%5B%28%28-E_1+-+E_2%29lambda%29%5E2+-4%28E_1+E_2+-V_1+V_2+lambda%5E2%29%5D%2F2 aus.
Also die nullte Ordnung überlebt, die erste fällt weg, die zweite überlebt wieder usw. Für kleine lambda könnte man ja mit der ersten erst einmal zufrieden sein denke ich. Ist das so okay?
Weiterhin soll ich dann die zeitliche entwicklung eines Zustandes |t> für diesen Spezialfall diskutieren, wenn für t=0 gilt: |t=0> = |1> .. da bin ich aber völlig aufgeschmissen. Wie setzt man da an? |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8583
|
 jh8979 Verfasst am: 24. Jun 2014 15:18 Titel: jh8979 Verfasst am: 24. Jun 2014 15:18 Titel: |
 |
|
| escapado hat Folgendes geschrieben: | Also so wie ich es aufgeschrieben habe sind die eigenvektoren jeweils so schon linearkombinationen weil ich als basis ja |1> und |2> gewählt habe. Damit ist jeweils der erste Eintrag in dem Vektor der Koeffizient des Basisvektors |1> und der zweite Eintrag entsprechend der Koeffizient des Basisvektors |2>. Damit habe ich das also fertig.
Die sind aber jetzt noch nicht zwingend normiert oder?
|
Richtung und richtig.
| Zitat: |
Ich bin mir jetzt leider nicht ganz sicher wie ich das entwickeln soll? Soll ich einer Taylorreihe um lambda = 0 darstellen?
|
Auch richtig, da geht sogar per Hand mit ^x \approx 1 + x \epsilon + \dots)
| Zitat: |
Weiterhin soll ich dann die zeitliche entwicklung eines Zustandes |t> für diesen Spezialfall diskutieren, wenn für t=0 gilt: |t=0> = |1> .. da bin ich aber völlig aufgeschmissen. Wie setzt man da an? |
Wodurch ist denn die Zeitentwicklung bestimmt in der QM?
PS: Deine Formel für E stimmt im letzten Post nicht ganz ... |
|
 |
escapado
Anmeldungsdatum: 08.05.2013
Beiträge: 49
|
 escapado Verfasst am: 24. Jun 2014 16:22 Titel: escapado Verfasst am: 24. Jun 2014 16:22 Titel: |
 |
|
Okay danke.
Ja, da ist was schief gelaufen mit dem lambda. Es sollte dann wohl eher heißen:
^2-4(E_1E_2+V_{12}V_{21}\lambda^2)}}{2} = \frac{E_1+E_2}{2} \pm \sqrt{\left(\frac{E_1-E_2}{2}\right)^2+V_{12}V_{21}\lambda^2})
So müsste es jetzt richtig sein.
Wenn ich das nun Taylorentwickle um lambda=0 erhalte ich:
 \right) \pm \frac{\lambda^2 V_{12} V_{21}}{(E_1-E_2)} +O(\lambda^4))
Oder eben wieder nur den ersten Term. Damit sind die Energieeigenwerte für diesen Spezialfall identisch mit denen die man vorher auch hatte, also  in erster Ordnung. Das ist doch schonmal ein gutes Ergebnis finde ich. in erster Ordnung. Das ist doch schonmal ein gutes Ergebnis finde ich.
Also wir haben bisher immer nur mit der zeitunabhängigen SG gerechnet. Leider hat unser Dozent nichts weiter verraten aber etwas recherche hat mich auf den Zeitentwicklungsoperator gebracht. Bin ich damit auf dem richtigen Weg?
Zuletzt bearbeitet von escapado am 24. Jun 2014 17:15, insgesamt einmal bearbeitet |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8583
|
 jh8979 Verfasst am: 24. Jun 2014 17:05 Titel: jh8979 Verfasst am: 24. Jun 2014 17:05 Titel: |
 |
|
| escapado hat Folgendes geschrieben: |
So müsste es jetzt richtig sein.
Wenn ich das nun Taylorentwickle um lambda=0 erhalte ich:
 \right) - \frac{\lambda^2 V_{12} V_{21}}{(E_1-E_2)} +O(\lambda^5))
Oder eben wieder nur den ersten Term. Damit sind die Energieeigenwerte für diesen Spezialfall identisch mit denen die man vorher auch hatte, also  in erster Ordnung. Das ist doch schonmal ein gutes Ergebnis finde ich. in erster Ordnung. Das ist doch schonmal ein gutes Ergebnis finde ich.
|
Ja, aber normalerweise soll man da schon bis zum ersten nicht-verschwindenden Term in lambda rechnen  dass für lambda=0 wieder E_1,2 rauskommen sollte ist ja klar dass für lambda=0 wieder E_1,2 rauskommen sollte ist ja klar 
| Zitat: |
Also wir haben bisher immer nur mit der zeitunabhängigen SG gerechnet. Leider hat unser Dozent nichts weiter verraten aber etwas recherche hat mich auf den Zeitentwicklungsoperator gebracht. Bin ich damit auf dem richtigen Weg?
|
Kann ich mir irgendwie nur schwer vorstellen. Zeitentwicklungsoperator ist schonmal gut (auch wenn dass bisschen mit Kanonen auf Spatzen schiessen ist  ). ). |
|
 |
escapado
Anmeldungsdatum: 08.05.2013
Beiträge: 49
|
 escapado Verfasst am: 24. Jun 2014 17:35 Titel: escapado Verfasst am: 24. Jun 2014 17:35 Titel: |
 |
|
Okay dann bin ich damit gut zufrieden.
Bei dem Zeitentwicklungsoperator.. also ich bin einmal die ganze Vorlesung durchgegangen und wir haben wirklich nie mit Zeitabhängigen Dingen gerechnet.
Wir haben die SG immer Zeitunabhängig gemacht indem wir einen Phasenfaktor ausgeklammert haben. Da war unser Potential z.B. immer Zeitunabhängig. Also ich würde sonst vermutlich einfach nur diese E-Funktion wieder dranmultiplizieren. Das wäre dann:

Aber das hilft ja noch nicht groß order?
Edit: Latex (und ein minus) <,<
Zuletzt bearbeitet von escapado am 25. Jun 2014 16:14, insgesamt 2-mal bearbeitet |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8583
|
 jh8979 Verfasst am: 24. Jun 2014 18:17 Titel: jh8979 Verfasst am: 24. Jun 2014 18:17 Titel: |
 |
|
| escapado hat Folgendes geschrieben: |
|t\rangle = e^{iHt/h} | 1\rangle
Aber das hilft ja noch nicht groß order? |
Nicht?  |
|
 |
escapado
Anmeldungsdatum: 08.05.2013
Beiträge: 49
|
 escapado Verfasst am: 25. Jun 2014 16:13 Titel: escapado Verfasst am: 25. Jun 2014 16:13 Titel: |
 |
|
Hmm also wenn Du so fragst, dann sicher doch. Ich habe halt überlegt ob man statt dem Hamilton in der E-Funktion die Eigenwerte einsetzen muss. Aber jetzt wird es etwas haarig. Also entweder ich setze da den Eigenwert E1 für den Hamilton ein (aber ich glaube das darf ich nicht) oder ich muss erst einmal den Zustand |1> durch eine Basistransformation durch meine neuen Eigenvektoren (nennen wir sie mal |+> und |-> ausdrücken, und dann hätte ich irgendetwas, was in seiner Form so aussehen sollte:

Wobei die beiden k-Faktoren aus der Basistransformation rauszubekommen wären. Ist das der richtige Ansatz oder kann ich mir das sparen? |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8583
|
 jh8979 Verfasst am: 25. Jun 2014 18:18 Titel: jh8979 Verfasst am: 25. Jun 2014 18:18 Titel: |
 |
|
|
Sieht gut aus. |
|
 |
|

















 ).
).