| Autor |
Nachricht |
Ikke
Gast
|
 Ikke Verfasst am: 20. Nov 2013 09:28 Titel: Relativistische Energie nach Impuls umstellen Ikke Verfasst am: 20. Nov 2013 09:28 Titel: Relativistische Energie nach Impuls umstellen |
 |
|
Meine Frage:
Die Gleichung für die relativistische Energie ist E²=(pc)²+(mc²)².
Wie lautet die Formel, wenn man sie nach dem relativistischen Impuls p umstellt?
Meine Ideen:
Ich komme einfach nicht drauf. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 20. Nov 2013 09:42 Titel: TomS Verfasst am: 20. Nov 2013 09:42 Titel: |
 |
|
Zunächst stellst du so um, das der Term mit p alleine auf einer Seite steht.
Dann ziehst du die Wurzel.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Ikke
Gast
|
 Ikke Verfasst am: 20. Nov 2013 09:44 Titel: Ikke Verfasst am: 20. Nov 2013 09:44 Titel: |
 |
|
OK, ich komme auf p²=(m²c^4+E²)/c²
Ist das richtig? |
|
 |
Ikke
Gast
|
 Ikke Verfasst am: 20. Nov 2013 09:57 Titel: Ikke Verfasst am: 20. Nov 2013 09:57 Titel: |
 |
|
|
Ich habe nochmal versucht, komme auf: p²=(E²-m^2c^4)/c^2 |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 20. Nov 2013 12:50 Titel: TomS Verfasst am: 20. Nov 2013 12:50 Titel: |
 |
|
ist ja nicht so schwer, oder?
E²=(pc)²+(mc²)²
(pc)² = E² - (mc²)²
p² = (E² - (mc²)²)/c²
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Ikke
Gast
|
 Ikke Verfasst am: 20. Nov 2013 14:40 Titel: Ikke Verfasst am: 20. Nov 2013 14:40 Titel: |
 |
|
Wie du siehst, habe ich noch einen anderen Beitrag eröffnet mit dem Thema Elektronenmikroskop.
Laut Wikipedia beträgt die De-Broglie-Wellenlänge für ein Elektron der Energie (Welche Energie? In Wiki steht weiter nichts) 100 keV 0,0037 nm.
Kannst du Tipps und Hilfe zur Berechnung geben? Wie komme ich von 100 keV Elektronenenergie auf 0,0037 nm?
Ich würde so vorgehen:
Als erstes muss man von der Gesamtenergie 100 keV (1,602*10^-14 Joule (falls das stimmt)) den relativistischen Impuls berechnen.
Das mache ich mit der Formel p² = (E² - (mc²)²)/c²
Jetzt wird bei mir der Wert des Impulses negativ, warum???
Weiter gehe ich mit der Formel lambda=h/p vor.
Aber ich komme nicht auf 0,0037 nm. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 20. Nov 2013 17:02 Titel: TomS Verfasst am: 20. Nov 2013 17:02 Titel: |
 |
|
| Ikke hat Folgendes geschrieben: | | Laut Wikipedia beträgt die De-Broglie-Wellenlänge für ein Elektron der Energie (Welche Energie? In Wiki steht weiter nichts) 100 keV 0,0037 nm. |
100 keV ist die kinetische Energie.
| Ikke hat Folgendes geschrieben: | | Das mache ich mit der Formel p² = (E² - (mc²)²)/c² |
Ja
| Ikke hat Folgendes geschrieben: | | Jetzt wird bei mir der Wert des Impulses negativ, warum??? |
Da musst du wohl einen Fehler drin haben. Wahrscheinlich weil du direkt die 100 keV einsetzt. Die 100keV sind jedoch die kinetische Energie; die obige Formel funktioniert jedoch mit der Gesamtenergie.
| Ikke hat Folgendes geschrieben: | | Weiter gehe ich mit der Formel lambda=h/p vor. |
Ja
Zusammenfassung der benötigten Formeln
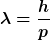
^2 + (mc^2)^2 )
 )
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Ikke
Gast
|
 Ikke Verfasst am: 20. Nov 2013 17:50 Titel: Ikke Verfasst am: 20. Nov 2013 17:50 Titel: |
 |
|
Wenn die 100 keV die relativistische kinetische Energie sind, wozu benötige ich dann die Formel für die Gesamtenergie?
Ich nehme an, dass ich von der kinetischen Energie irgendwie auf die Gesamtenergie rechnen kann, aber wie mache ich das?
Dann geht es weiter mit p² = (E² - (mc²)²)/c².
Der Rest ergibt sich dann. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 20. Nov 2013 21:51 Titel: TomS Verfasst am: 20. Nov 2013 21:51 Titel: |
 |
|
Nun, du musst auf den Impuls zurückrechnen, also
^2 = E^2 - (mc^2)^2)

Wenn du die zweite Gleichung in die erste einsetzt, dann kannst du den Impuls p durch die kinetische sowie die Ruhemasse ausdrücken. Beides ist bekannt.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Ikke
Gast
|
 Ikke Verfasst am: 21. Nov 2013 07:19 Titel: Ikke Verfasst am: 21. Nov 2013 07:19 Titel: |
 |
|
So, ich habe jetzt die richtige Berechnung hinbekommen. Komme genau auf 0,0037 nm.
Thank you. |
|
 |
Ikke
Gast
|
 Ikke Verfasst am: 21. Nov 2013 07:37 Titel: Ikke Verfasst am: 21. Nov 2013 07:37 Titel: |
 |
|
Also ich bin jetzt so vorgegangen:
Ich habe die Formel E=E_kin+mc² genommen. Damit habe ich die Gesamtenergie berechnet.
Dann bin ich vorgegangen mit der Formel p²=(E²-(mc²)²)/c²
Dann habe ich den Impuls in die Formel lambda=h/p eingesetzt.
Und heraus kam genau 0,0037 nm.
War die Vorgehensweise so richtig? |
|
 |
Ikke
Gast
|
 Ikke Verfasst am: 21. Nov 2013 13:04 Titel: Ikke Verfasst am: 21. Nov 2013 13:04 Titel: |
 |
|
Hi TomS.
Ich kopiere meine Frage nochmal, vielleicht hast du sie nicht gesehen.
Also ich bin jetzt so vorgegangen:
Ich habe die Formel E=E_kin+mc² genommen. Damit habe ich die Gesamtenergie berechnet.
Dann bin ich vorgegangen mit der Formel p²=(E²-(mc²)²)/c²
Dann habe ich den Impuls in die Formel lambda=h/p eingesetzt.
Und heraus kam genau 0,0037 nm.
War die Vorgehensweise so richtig? |
|
 |
Ikke
Gast
|
 Ikke Verfasst am: 21. Nov 2013 14:42 Titel: Ikke Verfasst am: 21. Nov 2013 14:42 Titel: |
 |
|
|
TomS, magst du mir nicht mehr antworten??? |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 21. Nov 2013 14:45 Titel: TomS Verfasst am: 21. Nov 2013 14:45 Titel: |
 |
|
Deine Vorgehensweise sieht vernünftig ist.
Magst du die gesamte Rechnung (in Formeln, nicht mit Werten) in LaTeX reinstellen?
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Ikke
Gast
|
 Ikke Verfasst am: 21. Nov 2013 14:50 Titel: Ikke Verfasst am: 21. Nov 2013 14:50 Titel: |
 |
|
Mit dem LaTeX komme ich nicht ganz klar, aber vielleicht wäre es gut, wenn du das machen würdest. Immerhin lesen ja einige Leute diese Beiträge, die die selbe Frage haben.
Formeln, die ich genommen habe:
1. E=E_kin+mc²
2. p²=(E²-(mc²)²)/c² (natürlich noch die Wurzel ziehen)
3. lambda=h/p |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 21. Nov 2013 15:02 Titel: TomS Verfasst am: 21. Nov 2013 15:02 Titel: |
 |
|
Das sollte ausreichen; vlt. bei Gelegenheit
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Ikke
Gast
|
 Ikke Verfasst am: 21. Nov 2013 15:03 Titel: Ikke Verfasst am: 21. Nov 2013 15:03 Titel: |
 |
|
|
Aber meine Vorgehensweise ist vernünftig? |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 21. Nov 2013 15:05 Titel: TomS Verfasst am: 21. Nov 2013 15:05 Titel: |
 |
|
Ja
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Ikke
Gast
|
 Ikke Verfasst am: 21. Nov 2013 15:17 Titel: Ikke Verfasst am: 21. Nov 2013 15:17 Titel: |
 |
|
Gerade noch ne Frage zu den 100 keV.
Wie kommst du darauf, dass das die kinetische Energie ist? |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 21. Nov 2013 15:18 Titel: TomS Verfasst am: 21. Nov 2013 15:18 Titel: |
 |
|
Weil's nur so Sinn macht; die Ruheenergie ist ja bereits 511 keV
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Ikke
Gast
|
 Ikke Verfasst am: 22. Nov 2013 08:48 Titel: Ikke Verfasst am: 22. Nov 2013 08:48 Titel: |
 |
|
|
Kann ich jetzt sicher sein, dass ich richtig gerechnet habe? Immerhin bin ich auf 0,0037 nm gekommen. |
|
 |
Ikke
Gast
|
 Ikke Verfasst am: 22. Nov 2013 16:35 Titel: Ikke Verfasst am: 22. Nov 2013 16:35 Titel: |
 |
|
|
Kann ich jetzt sicher sein, dass ich richtig gerechnet habe? Immerhin bin ich auf 0,0037 nm gekommen. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 22. Nov 2013 16:40 Titel: TomS Verfasst am: 22. Nov 2013 16:40 Titel: |
 |
|
Dein Rechenweg sieht vernünftig aus; du kommst auf das richtige Ergebnis; passt
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Ikke
Gast
|
 Ikke Verfasst am: 24. Nov 2013 09:26 Titel: Ikke Verfasst am: 24. Nov 2013 09:26 Titel: |
 |
|
Gute Elektronenmikroskope haben heute eine Auflösung von 0,05 nm.
Ein Elektron mit einer relativistischen kinetischen Energie hat aber bereits eine De-Broglie-Wellenlänge von nur 0,0037 nm.
Wie kann das sein? Haben die heutigen Elektronen in den Elektronenmiktroskopen einfach nicht genug kinetische Energie? |
|
 |
Ikke
Gast
|
 Ikke Verfasst am: 24. Nov 2013 09:44 Titel: Ikke Verfasst am: 24. Nov 2013 09:44 Titel: |
 |
|
Nachtrag von siehe oben.
Laut meinen Berechnungen wäre die De-Broglie-Wellenlänge für ein Elektron der relativistischen kinetischen Energie 0,00196 nm.
Stimmst du damit überein? |
|
 |
Ikke
Gast
|
 Ikke Verfasst am: 24. Nov 2013 09:45 Titel: Ikke Verfasst am: 24. Nov 2013 09:45 Titel: |
 |
|
Nochmal Nachtrag:
Laut meinen Berechnungen wäre die De-Broglie-Wellenlänge für ein Elektron der relativistischen kinetischen Energie von 300 keV gleich 0,00196 nm.
Stimmst du damit überein? |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 24. Nov 2013 09:53 Titel: TomS Verfasst am: 24. Nov 2013 09:53 Titel: |
 |
|
Ich denke, dass es sich bei der Materiewellenlänge nur um eine theoretisch mögliche Auflösung handelt, und dass Linsenfehler der eigtl. begrenzende Faktor sind. Ich bin da aber kein Experte.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Ikke
Gast
|
 Ikke Verfasst am: 24. Nov 2013 09:56 Titel: Ikke Verfasst am: 24. Nov 2013 09:56 Titel: |
 |
|
Das denke ich auch.
Noch ne andere Frage. Laut meinen Berechnungen wäre die De-Broglie-Wellenlänge für ein Elektron der relativistischen kinetischen Energie von 300 keV gleich 0,00196 nm.
Stimmst du damit überein? |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 24. Nov 2013 10:13 Titel: TomS Verfasst am: 24. Nov 2013 10:13 Titel: |
 |
|
Physik
Lass' uns nochmal die Formeln zusammenfassen
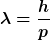
^2 + (mc^2)^2 )
 )
Üblicherweise wird die kinetische statt der Gesamtenergie angegeben. Außerdem verwenden wir die Ruheenergie statt der Ruhemasse
^2 = E^2 - E_0^2)

Einsetzen liefert
^2 = E^2 - E_0^2 = ( E_\text{kin} + E_0 )^2 - E_0^2 = E_\text{kin}^2 + 2 \, E_0 \, E_\text{kin} )
Für die Wellenlänge folgt dann

Stimmt das mit deinen Formeln überein?
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago.
Zuletzt bearbeitet von TomS am 26. Nov 2013 07:45, insgesamt einmal bearbeitet |
|
 |
Ikke
Gast
|
 Ikke Verfasst am: 24. Nov 2013 10:23 Titel: Ikke Verfasst am: 24. Nov 2013 10:23 Titel: |
 |
|
Ich habe nochmal deine Formel nachgerechnet und ich stimme absolut überein.
Damit sollte ich jetzt sicher sein, dass die de-Broglie-Wellenlänge für ein Elektron der kinetischen Energie von 300 keV genau 0,00196 nm beträgt.
Thank you very much! |
|
 |
Ikke
Gast
|
 Ikke Verfasst am: 24. Nov 2013 12:18 Titel: Ikke Verfasst am: 24. Nov 2013 12:18 Titel: |
 |
|
Du scheinst dich ja wirklich gut auszukennen! Es ist sehr nett, dass du mir und anderen hilfst.
Ich denke, da unsere Formeln übereinstimmen, wir aufs selbe Ergebnis kommen. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 24. Nov 2013 12:23 Titel: TomS Verfasst am: 24. Nov 2013 12:23 Titel: |
 |
|
Danke ;-)
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Ikke
Gast
|
 Ikke Verfasst am: 25. Nov 2013 07:18 Titel: Ikke Verfasst am: 25. Nov 2013 07:18 Titel: |
 |
|
Immer wenn die relativistische kinetische Energie gegeben ist für ein Teilchen und ich möchte die de-Broglie Wellenlänge berechnen, dann nehme ich die Formel: lambda=hc/Wurzel(E_kin²+2*E_0*E_kin).
Ansonsten nehme ich, sollte der relativistische Impuls gegeben sein, die Formel lambda=h/p. |
|
 |
Ikke
Gast
|
 Ikke Verfasst am: 25. Nov 2013 11:02 Titel: Ikke Verfasst am: 25. Nov 2013 11:02 Titel: |
 |
|
|
Eigentlich kann ich doch immer die Formel lambda=hc/Wurzel(E_kin²+2*E_0*E_kin) nehmen, wenn ich die De-Broglie-Wellenlänge berechnen möchte, oder? |
|
 |
Ikke
Gast
|
 Ikke Verfasst am: 25. Nov 2013 12:02 Titel: Ikke Verfasst am: 25. Nov 2013 12:02 Titel: |
 |
|
Warum antwortest du mir nicht mehr???
Habe noch folgende Fragen:
Immer wenn die relativistische kinetische Energie gegeben ist für ein Teilchen und ich möchte die de-Broglie Wellenlänge berechnen, dann nehme ich die Formel: lambda=hc/Wurzel(E_kin²+2*E_0*E_kin).
Ansonsten nehme ich, sollte der relativistische Impuls gegeben sein, die Formel lambda=h/p.
Eigentlich kann ich doch immer die Formel lambda=hc/Wurzel(E_kin²+2*E_0*E_kin) nehmen, wenn ich die De-Broglie-Wellenlänge berechnen möchte, oder? |
|
 |
IchAuch
Gast
|
 IchAuch Verfasst am: 25. Nov 2013 13:57 Titel: IchAuch Verfasst am: 25. Nov 2013 13:57 Titel: |
 |
|
@TomS
Wie wäre es denn, wenn man ein Elektron nimmt, welches durch eine Spannung von U = 2000 Volt beschleunigt wird.
Ein Elektron, das diese Spannung durchläuft hat doch genau eine (relativistische) kinetische Energie von 2000 Elektronenvolt.
Also kann man doch die Formel von dir nehmen, um auf die Wellenlänge zu kommen.
Man verfährt wie beschrieben bzw. wie gehabt. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 25. Nov 2013 15:05 Titel: TomS Verfasst am: 25. Nov 2013 15:05 Titel: |
 |
|
| TomS hat Folgendes geschrieben: | 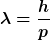
^2 = E^2 - E_0^2 = ( E_\text{kin} + E_0 )^2 - E_0^2 = E_\text{kin}^2 + 2 \, E_0 \, E_\text{kin} )
 |
Ich weiß nicht, was zu diesen Formeln noch fehlt.
Die Herleitung ist allgemeingültig, man muss nur noch anwenden.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago.
Zuletzt bearbeitet von TomS am 26. Nov 2013 07:46, insgesamt einmal bearbeitet |
|
 |
Ikke
Gast
|
 Ikke Verfasst am: 26. Nov 2013 07:24 Titel: Ikke Verfasst am: 26. Nov 2013 07:24 Titel: |
 |
|
Bei der Herleitung der Formel lambda=hc/Wurzel(E_kin²+2*E_0*E_kin) habe ich ein Problem.
Also (pc)²=E²*E_0² soweit ist klar
aber dann schreibst du (pc)²=E²*E_0²=(E_kin+E_0²)²
warum ist (E_kin+E_0²)² ?
Warum ist zweimal E_0 hoch zwei? |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 26. Nov 2013 07:47 Titel: TomS Verfasst am: 26. Nov 2013 07:47 Titel: |
 |
|
| Ikke hat Folgendes geschrieben: | | warum ist (E_kin+E_0²)² ? |
Das war natürlich ein Schreibfehler, kann ja schon bzgl. der Dimensionen nicht stimmen. Hab's korrigiert.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Ikke
Gast
|
 Ikke Verfasst am: 26. Nov 2013 07:56 Titel: Ikke Verfasst am: 26. Nov 2013 07:56 Titel: |
 |
|
OK. Ich habe mir echt schon die Zähne an der zweiten "hoch zwei" ausgebissen. ;-)
Man könnte aber doch auch schreiben:
Für p (Impuls): p=[Wurzel(E²-E_0²)]/c
Dann einsetzen in lambda=h/p |
|
 |
|















