| Autor |
Nachricht |
Mathomat
Gast
|
 Mathomat Verfasst am: 29. Sep 2013 18:32 Titel: Wie löst man diese Gleichungsart?? Mathomat Verfasst am: 29. Sep 2013 18:32 Titel: Wie löst man diese Gleichungsart?? |
 |
|
Hallo allerseits,
ich sitze hier hobbymäßig vor einer Gleichung, bei der ich nicht richtig weiter komme. Aber das kann doch nicht so schwer sein..
Also gegeben sei eine "Sin-Cos-Summe", z.B.
+a2*cos(p) )
oder noch besser
*cos(q)+a2*cos(p)*cos(q)+a3*sin(q) )
...und so weiter...
Gibt's hier einen generellen Lösungsweg für p oder q ???
Kann mir da jemand weiter helfen?
Bis dann |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 29. Sep 2013 18:42 Titel: TomS Verfasst am: 29. Sep 2013 18:42 Titel: |
 |
|
Die Gleichung ist i.A. nicht geschlossen lösbar
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
-
Gast
|
 - Verfasst am: 29. Sep 2013 18:46 Titel: - Verfasst am: 29. Sep 2013 18:46 Titel: |
 |
|
Eine Gleichung mit zwei Unbekannten? Da wird es wohl ohnehin keine eindeutige Lösung geben.
Da du kein konkretes Problem zu haben sondern eher allgemein zu fragen scheinst, ist vielleicht der Hinweis auf de.wikipedia.org/wiki/Formelsammlung_Trigonometrie nützlich. |
|
 |
Mathomat
Gast
|
 Mathomat Verfasst am: 29. Sep 2013 22:19 Titel: Mathomat Verfasst am: 29. Sep 2013 22:19 Titel: |
 |
|
Hmm, danke.
Sicher, dass das nicht geht?
Z.B. bei der ersten Gleichung muss ich doch die Summe nur als ein "r*sin(p+phi)" darstellen, und kann dann nach p auflösen.
..Die Formel dafür gibts übrigens auch in der Formelsammlung..
Ich frage mich, ob es da einen allgemeinen 'komplexen' Umweg gibt, mit dem dann auch die untere Gleichung lösbar wird...?!
Und noch was zur Formelsammlung: Welche mathematische Umgebung ist denn die geeigneteste um die ganzen (bzw einen Großteil) der Formeln herleiten zu können?? |
|
 |
Jayk
Anmeldungsdatum: 22.08.2008
Beiträge: 1450
|
 Jayk Verfasst am: 29. Sep 2013 22:32 Titel: Jayk Verfasst am: 29. Sep 2013 22:32 Titel: |
 |
|
Die erste Gleichung kann man auch ohne komplexe Zahlen losen (eine so genannte goniometrische Gleichung, Stoff Klasse 10).
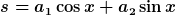
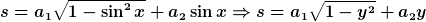
Umstellen:
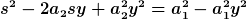
 (a_1^2 + a_2^2)}}{a_1^2 + a_2^2})
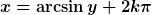 |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 29. Sep 2013 23:02 Titel: TomS Verfasst am: 29. Sep 2013 23:02 Titel: |
 |
|
Für mehr Terme wird das i.A. nicht funktionieren
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Mathomat
Gast
|
 Mathomat Verfasst am: 29. Sep 2013 23:43 Titel: Mathomat Verfasst am: 29. Sep 2013 23:43 Titel: |
 |
|
Auch nicht schlecht, auch wenn ich "goniometrisch" selbst in der 10. Klasse nicht gehört habe.. (an wem genau das liegt bleibt offen..).
Aber die Frage ist ja eigentlich, ob z.B. die 2. Gleichung überhaupt (komplex)
lösbar ist..?!
Kann es sein, dass trig. Gleichungen recht viele Gestalten haben können?!
TomS, beziehst du dich jetzt auf Jayk oder auf mich? Also "garnicht lösbar", oder "nicht goniometrisch lösbar"?? |
|
 |
Feucht von Lipwig
Anmeldungsdatum: 19.09.2013
Beiträge: 122
|
 Feucht von Lipwig Verfasst am: 30. Sep 2013 09:02 Titel: Feucht von Lipwig Verfasst am: 30. Sep 2013 09:02 Titel: |
 |
|
| Mathomat hat Folgendes geschrieben: |
Kann es sein, dass trig. Gleichungen recht viele Gestalten haben können?!
|
Natürlich, man kann schließlich aufschreiben was man möchte - der Kreativität sind keine Grenzen gesetzt.
| Zitat: | | TomS, beziehst du dich jetzt auf Jayk oder auf mich? Also "garnicht lösbar", oder "nicht goniometrisch lösbar"?? |
Nicht geschlossen lösbar!
Lösungen können existieren, entweder exakt oder als Grenzwert.
Man kann jedoch nicht jede Gleichung durch gewöhnliche Umformungen nach der gewünschten Variablen Umstellen.
Ein Beispiel für eine recht einfache aber nicht mehr geschlossen lösbare Gleichung ist: x = tanx.
Neben der Nulll lassen sich analytisch keine weitere Lösungen finden, obwohl sie existieren. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 30. Sep 2013 09:04 Titel: TomS Verfasst am: 30. Sep 2013 09:04 Titel: |
 |
|
Nun, zunächst müssen wir uns darauf einigen, dass wir immer nur von einer Unbekannten q reden (für zwei Unbekannte p und q oder mehr brauchst du auch zwei Gleichungen oder mehr; dann hättest du aber ein nicht-lineares Gleichungssystem, und die sind nur in absoluten Spezialfällen exakt lösbar).
Die Methode des Umstellens
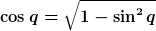
funktioniert zunächst natürlich immer. Allerdings hast du dann ein algebraisches Gleichungssystem mit Wurzelausdrücken. Dabei entstehen zwei Schwierigkeiten:
1) je nach Kombination von Winkelfunktionen (in deiner zweiten Gleichung) ist es nicht immer möglich, alle Wurzeln durch Quadrieren (oder höhere Potenzen) tatsächlich zum Verschwinden zu bringen. Wenn das nicht gelingt, dann liegt kein Polynom vor, und du kannst die Gleichung nicht geschlossen lösen
2) selbst wenn es gelingt, die Gleichung in ein Polynom zu überführen, dann wird dieses i.A. von höherem Grad als zwei sein. Polynome sind aber nur bis einschließlich viertem Grad geschlossen lösbar; ab fünftem Grad sind sie dies i.A. nicht.
Du wirst also i.A. keine geschlossen lösbare Gleichung erhalten.
Besser geht man übrigens wie folgt vor:
Man eliminiert Winkelfunktionen mittels komplexer e-Funktionen, d.h. man verwendet
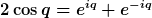
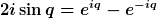
Damit erhält man sofort und ohne jeden Wurzelausdruck ein Polynom in
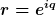
Negative Potenzen von r kann man durch Durchmultiplizieren eliminieren. Diese Vorgehensweise hat den Vorteil, dass sie das Scheinproblem (1) eliminiert und sofort auf das eigentliche Problem (2) führt, jedoch dahingehend vereinfacht, dass das Polynom nicht in sin und cos sondern in r vorliegt. D.h. man erhält eine Polynomgleichung
 = \sum_{n=0} p_n r^n = 0)
Für diese kann man sofort entsprechend (2) die Lösbarkeit ablesen:
- bis einschließlich viertem Grad: geschlossen lösbar
- ab fünftem Grad: i.A. nicht geschlossen lösbar (Untersuchung der Galois-Gruppe)
- Anzahl der Lösungen entspricht immer dem Grad des Polynoms (mit i.A. komplexem r und q)
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Mathomat
Gast
|
 Mathomat Verfasst am: 01. Okt 2013 20:03 Titel: Mathomat Verfasst am: 01. Okt 2013 20:03 Titel: |
 |
|
Ok, ich habe das mal für den ersten einfachen Fall durchgespielt.. Mit einigen Tricks gehts auch.
Aber mich würde mal interessieren, wie du praktisch die 1. Gleichung mittels komplexer e-Fkt. löst. Und zwar so, dass sozusagen nachher aus den beiden trig. Fkt. ohne Phase, eine trig. Fkt. mit Phase wird (nach der man dann auflösen kann).
Vielleicht lerne ich daraus etwas für komplexere Probleme...
Und was meinst du mit "Durchmultiplizieren"? Das würde ich jetzt eher mit rationalen Gleichungen in Verbindung bringen...
Und noch eine andere Frage: Das verrückte ist ja, -ich habe hier natürlich ein Gleichungssystem für mehrere Unbekannte-, dass ich eine graphische Lösung für die Winkel gefunden habe, ich sie aber nicht algebraische herleiten kann...
Ums kurz zu machen: Das Gleichungssystem wäre z.B. eine LK einer in Kugelkoordinaten gedrehten Basis..
Also sowas wie
)_i )
Entsprechendes für r_y und r_z. trig() steht für sin() und cos()..
Es kann doch nicht sein, dass man eine graphische Lösung findet, aber keine algebraische... oder doch?!? |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 01. Okt 2013 20:44 Titel: TomS Verfasst am: 01. Okt 2013 20:44 Titel: |
 |
|
| Mathomat hat Folgendes geschrieben: | | Aber mich würde mal interessieren, wie du praktisch die 1. Gleichung mittels komplexer e-Fkt. löst. |
Also wir starten mit
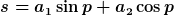
Wir benutzen
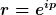
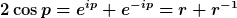
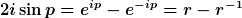
Wir setzen ein
 + a_2 \left(r + r^{-1} \right) )
und multiplizieren mit einer geeigneten Potenz von r durch, um die negativen Potenzen loszuwerden, hier einfach mit r
 + a_2 \left(r^2 + 1 \right) )
Zusammenfassen der Potenzen liefert
 = (a_2 - ia_1) r^2 - 2sr + (a_2 + ia_1) = 0)
Die beiden Lösungen für r erhält man mittels der bekannten Formel für quadratische Gleichungen, wobei i.A. sowohl die Koeffizienten als auch r komplex sind. Es ist klar, dass für ein Polynom zweiten Grades immer genau zwei Lösungen existieren (Fundamentalsatz der Algebra).
Für die Bestimmung von p aus r benötigt man natürlich den komplexen Logarithmus, und die Lösung dazu ist aufgrund der Periodizität nicht eindeutig, aber die Gleichung ist immer lösbar.
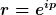
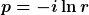
http://en.wikipedia.org/wiki/Logarithm#Complex_logarithm
| Mathomat hat Folgendes geschrieben: | | Es kann doch nicht sein, dass man eine graphische Lösung findet, aber keine algebraische... oder doch?!? |
Ich habe das oben evtl. nicht exakt genug erklärt. Gegeben sei eine Gleichung in n (komplexen Variablen). Die Lösungsmenge ist i.A. n-1 dimensional, d.h.
n=1, n-1=0: für eine Gleichung in einer Variablen ist die Lösung i.A. ein Punkt (oder wegen der Mehrdeutigkeit des Logarithmus eine Schar von Punkten)
n=2, n-1=1: für eine Gleichung in zwei Variablen ist die Lösung i.A. eine eindimensionale komplexe Mannigfaltigkeit = eine komplexe Kurve (oder wegen der Mehrdeutigkeit des Logarithmus eine Schar von Kurven)
...
D.h. dass tatsächlich Lösungen existieren, aber eben weder eindeutige noch explizit konstruierbare.
Im Allgemeinen definiert eine Polynomgleichung
 = 0)
in n Variablen eine n-1 dimensionale algebraische Fläche in einem n-dimensionalen (komplexen!) Raum.
http://en.wikipedia.org/wiki/Algebraic_surface
Diese Strukturen sind insgs. sehr gut verstanden.
Dein Problem ist jetzt aber, dass du nicht an den Lösungen in r sondern in p interessiert bist, und dazu benötigst wie gesagt den komplexen Logarithmus. In einer Variablen ist das explizit mittels Riemannschen Flächen beschreibbar
http://en.wikipedia.org/wiki/Riemann_surface
aber in mehreren Variablen musst du sozusagen Riemannsche Mannigfaltigkeiten über höherdimensionalen algebraischen Flächen untersuchen. Das ist sicherlich extrem spannend - aber ich habe ehrlich gesagt keine Ahnung, wie man da vorgeht. Lass' es mich wissen, wenn du was rausgefunden hast.
EDIT:
http://www.physicsforums.com/showthread.php?p=4522729#post4522729
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Mathomat
Gast
|
 Mathomat Verfasst am: 15. Okt 2013 19:08 Titel: Mathomat Verfasst am: 15. Okt 2013 19:08 Titel: |
 |
|
Bevor ich es wieder vergesse schreibe ich jetzt...
Ist nun natürlich klar, was du mit Duchmultiplizieren meintest...
Wenn ich also ein Polynom in "r = e^(i*p)" habe, kann ich dann bei der Lösung annehmen, dass der Betrag |r| = 1 ?!
Das würde doch neue Beziehungen zw. den Variablen von denen r abhängt schaffen (oder zumindest bestätigen)?! ..Das würde mich aber irgendwie wundern.. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 15. Okt 2013 22:06 Titel: TomS Verfasst am: 15. Okt 2013 22:06 Titel: |
 |
|
| Mathomat hat Folgendes geschrieben: | | Wenn ich also ein Polynom in "r = e^(i*p)" habe, kann ich dann bei der Lösung annehmen, dass der Betrag |r| = 1 ?! |
Nein, das kannst du nicht annehmen. r als Lösung eines Polynoms ist i.A. komplex, und p muss ebenfalls nicht reell sein.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Mathomat
Gast
|
 Mathomat Verfasst am: 16. Okt 2013 00:33 Titel: Mathomat Verfasst am: 16. Okt 2013 00:33 Titel: |
 |
|
Naja soo allgemein ist es hier ja nicht.. Also nur um nochmal sicher zu gehen:
Die Lösung des Polynoms sei von der Form
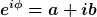 . .
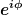 sitzt doch auf dem Einheitskreis... Damit sollte doch sitzt doch auf dem Einheitskreis... Damit sollte doch 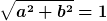 sein... sein...
Aber was soll uns das sagen?! |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 16. Okt 2013 06:47 Titel: TomS Verfasst am: 16. Okt 2013 06:47 Titel: |
 |
|
Warum sollte das auf dem Einheitskreis sitzen? Warum willst du das voraussetzen?
Für die allgemeine Lösung der Polynomgleichung P(r) = 0 gilt das offensichtlich nicht. Der Vorteil des Ansatzes ist ja gerade, dass du die Gleichung in r formulierst; damit entfällt die Bedingung |r| = 1 zunächst. Evtl. kannst du sie später wieder als Zusatzbedingung einführen.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Mathomat
Gast
|
 Mathomat Verfasst am: 16. Okt 2013 17:46 Titel: Mathomat Verfasst am: 16. Okt 2013 17:46 Titel: |
 |
|
Also wenn z.B. cos(x) = (e^(ix)+e^(-ix))/2, dann ist x doch real, und e^i.." sollte die Länge 1 haben, da der cos() eben diese Amplitude besitzt..
..Oder etwa nicht?!
..Ich habe nun 2 Gleichungen nach "e^(ip)" umgeformt und gleichgesetzt.. Bringt mich leider auch nicht viel weiter. Mit dem Polynomansatz habe ich also aus einer LK eine andere LK gemacht, die aber irgendwie auch nicht mehr preisgibt.. ..oder wie löst man Summen von Wurzeln?!
Also wenn es nicht noch irgendeine Möglichkeit gibt, siehts düster aus.
Wenn man das hätte herleiten können, wäre ich mir wenigstens sicher, dass es stimmt. Bei der graphischen Lösung bin ich nicht sicher.
Und dazu kommt noch, dass ich mir nicht vorstellen kann, dass es eine graphische, aber keine algebraische Lösung gibt.. (mit graphisch meine ich nicht nummerisch, sondern über Vektorlagen im Raum usw).
Algebraisch ist es oft umständlicher, aber mir ist noch nicht aufbefallen, dass es garnicht geht. Kennt zufällig jemand ein prominenteres Beispiel dazu?? |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 16. Okt 2013 19:31 Titel: TomS Verfasst am: 16. Okt 2013 19:31 Titel: |
 |
|
Nochmal zurück zum Anfang.
Du wirst i.A. dem Gleichungssystem formuliert mit Sinus und Cosinus nicht viel abgewinnen können. Also formulierst du es in ein Polynom P(r) um, wobei eben gerade nichts mehr über r und p vorausgesetzt wird. Beide sind zunächst beliebige komplexe Zahlen und ergeben sich auschließlich aus der Lösung P(r) = 0. Die Anzahl der Lösungen ist exakt bekannt (Grad des Polynoms), wenn auch i.A. nicht explizit konstruierbar (für Grad > 4). Diese Polynomgleichungen sind Standard in der Algebra (Galoisgruppe).
D.h. statt zuerst |r| = 1 zu fordern (was äquivalent zur Darstellung mit reellem Sinus und Cosinus ist) und anschließend die Gleichung zu lösen, löst du zuerst die Gleichung und sonderst anschließend diejenigen Lösungen aus, die |r| = 1 erfüllen (was die Zahl der für dich wichtigen Lösungen ggf. reduziert).
Das wäre zumindest die in der Algebra verwendete Vorgehensweise.
Was ist eigtl. deine Aufgabenstellung? Wie kommst du drauf?
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Mathomat
Gast
|
 Mathomat Verfasst am: 19. Okt 2013 17:49 Titel: Mathomat Verfasst am: 19. Okt 2013 17:49 Titel: |
 |
|
Ich glaube da hast du mich falsch verstanden. Ich wollte nicht zuerst |r|=1 setzen..
Ich sehe das so: Wenn cos(x) = (e^(i*x) - e^(-i*x))/2, dann ist x wohl real, und bleibt es auch. Das gilt dann auch für sin(x).
So nun wird jeder sin() und cos() durch die e^..-Summe ersetzt und die Gleichung wird nach e^(i*x) aufgelöst.
Da x real ist, der Exponent also rein imaginär, wäre e^(i*x) ein komplexer Zeiger auf dem Einheitskreis, für den eben |e^(i*x)| = 1 gilt.
Warum soll x plötzlich auch komplex sein?
Wenn man damit, dass |e^(i*x)| = 1 gelten muss, falsche Lösungen eliminieren kann, frage ich mich allerdings, warum sie überhaupt entstehen konnten.
Aber dann würde die Zusatzbedingung wenigstens Sinn machen.
Okay, hier mal ein konkretes Beispiel:
Wir nehmen ein gedrehtes KS im R^3. Ein Vektor (r) und die Komponenten des Vektors im gedrehten KS (k1, k2, k3) seien bekannt..
 \\ sin(\phi) \\ 0 \end{pmatrix} + k2 \begin{pmatrix} - sin(\phi) cos(\theta) \\ cos(\phi) cos(\theta) \\ sin(\theta) \end{pmatrix} + k3 \begin{pmatrix} sin(\phi) sin(\theta) \\ - cos(\phi) sin(\theta) \\ cos(\theta) \end{pmatrix} )
..Wenn das zu einfach sein sollte, könnte man auch z.B. k3 als unbekannt ansehen..
Bei Kugelkoordinaten ist es ja eigentlich nicht schwer die Orientierung des gedrehten KS graphisch zu bestimmen. Und ich wudere mich immernoch, dass das algebraisch ungleich schwerer, oder evtl. sogar unmöglich ist.
Und noch ein Nachtrag zum Beginn dieses Themas. Da hatte ich ja klein angefangen mit "f(x) = a1*sin(x) + a2*cos(x)".
Daraus lässt sich (auch laut Wiki-Formelsammlung) ein (reeller) Sinus mit veränderter Amplitude und Phase machen.
TomS, du hattest mir das zwar schon vorgerechnet, aber nur bis zum komplexen ln.. Wie mache ich denn daraus letztendlich wieder einen reellen Sinus der Form "r*sin(x+p)", bzw. die Formel die auch in der Sammlung zu finden ist?!
Unabhängig davon: Danke erstmal bis hierher! |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 20. Okt 2013 09:33 Titel: TomS Verfasst am: 20. Okt 2013 09:33 Titel: |
 |
|
| Mathomat hat Folgendes geschrieben: | Ich glaube da hast du mich falsch verstanden. Ich wollte nicht zuerst |r|=1 setzen..
Ich sehe das so: Wenn cos(x) = (e^(i*x) - e^(-i*x))/2, dann ist x wohl real, und bleibt es auch. Das gilt dann auch für sin(x). |
Aber genau das tust du! Wenn du x auf reelle Werte einschränkst, dann ist auch unmittelbar |r|=1.
Wenn du aber zuerst eine formale Umformung von einer Gleichung mit reellem sin und cos zu P(r) durchführst und etwas über die Lösungen der Polynomgleichungen lernen willst, dann solltest du diese Einschränkung zunächst fallen lassen, d.h. erst für r allgemein lösen (unabhängig von |r|) und anschließend diese Bedingung wieder einführen.
| Mathomat hat Folgendes geschrieben: | | Warum soll x plötzlich auch komplex sein? |
Weil wir es zulassen ;-)
| Mathomat hat Folgendes geschrieben: | | Okay, hier mal ein konkretes Beispiel ... |
Und welche Gleichung willst du jetzt lösen? Du bist ja mit einer Gleichung gestartet, die sehe ich nicht.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 21. Okt 2013 05:49 Titel: TomS Verfasst am: 21. Okt 2013 05:49 Titel: |
 |
|
| Mathomat hat Folgendes geschrieben: | Und noch ein Nachtrag zum Beginn dieses Themas. Da hatte ich ja klein angefangen mit "f(x) = a1*sin(x) + a2*cos(x)".
Daraus lässt sich (auch laut Wiki-Formelsammlung) ein (reeller) Sinus mit veränderter Amplitude und Phase machen ... Wie mache ich denn daraus letztendlich wieder einen reellen Sinus der Form "r*sin(x+p)" ...! |
Nun, das wäre wiederum einen Ansatz der obigen Form mit e-Funktion wert.
 + a_2 \cos(x) = b \sin(x+x_0))
Umschreiben mittels
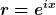

liefert
 + a_2 \,\left(r + r^{-1}\right) = -i\,b\,\left(r\,r_0 - r^{-1}\,r_0^{-1}\right))
Durchmultiplizieren mit r, sortieren nach Potenzen von r sowie separates Nullsetzen je Potenz vor r liefert zwei Gleichungen für zwei Unbekannte
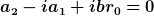
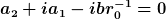
Die beiden Gleichungen kannst du nun nach den Unbekannten auflösen.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago.
Zuletzt bearbeitet von TomS am 23. Okt 2013 23:14, insgesamt einmal bearbeitet |
|
 |
Mathomat
Gast
|
 Mathomat Verfasst am: 23. Okt 2013 18:59 Titel: Mathomat Verfasst am: 23. Okt 2013 18:59 Titel: |
 |
|
Okay, so geht's auch...
Ich wollte nur mal sehen, was du so mit dem Winkel machst. Die eigentliche Annahme sollte auch gewesen sein, dass man die rechte Seite garnicht kennt;
aber wie gesagt, so geht's auch.
Ich glaube du hast ein ^(-1) bei einem r_0 vergessen...
Außerdem habe ich mal etwas 'rum gerechnet.
Ich habe so das gefühl, das |r|=1 immer gilt. Und das finde ich auch logisch.
Aber daraus ergibt sich eine kleines neues Problem:
Da man i.a. min. 2 Lsg. erhält, kann man |r|=1 nicht dazu nutzen die richtige auszuwählen (da dies ja eh für beide gilt).
Die Frage ist also, wie man dann direkt die richtige Lösung identifiziert..?!
Und noch eine andere Frage: In wieweit würden mich Quaternionen hier weiter bringen? (Oder ab wann...?!)
...hat ja irgendetwas mit Drehungen zu tun..
PS.: Du scheinst deine Beiträge hier protionsweise zu erstellen, ist natürlich praktisch, um sich Zeit lassen zu können (wenn ich das richtig sehe), aber mich hat es doch etwas verwirrt. Wenn man dann nicht davon ausgeht, dass noch mehr kommt, kann man sich schon wundern, ob das schon alles sein soll, sofern man mal die Chance hat dir beim Schreiben zuzusehen...
...Man muss eben wissen, dass da noch mehr kommen kann... |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 23. Okt 2013 21:15 Titel: TomS Verfasst am: 23. Okt 2013 21:15 Titel: |
 |
|
Ich denke nicht, dass ein ^{-1} fehlt; wo soll das sein?
In diesem Fall gilt (für reelle a1 und a2 tatsächlich |r| = 1; aber im allgemeinen Fall muss diese nicht der Fall sein. Bsp. Schnittpunkt Kreis mit Gerade: wenn kein Schnittpunkte im Reellen vorliegen, müssen diese zwingend im Komplexen liegen; did Anzahl der Lösungen einer Polynomgleichung P(r) = 0 sind ausschließlich vom Grad des Polynoms abhängig.
Quaternionen liefern lediglich eine andere (einfachere) Darstellung einer Drehung. Ich denke nicht, dass sich die Frage grundsätzlich ändert, die Struktur der Polynome ändert sich, der Grad und die Anzahl nicht.
Sorry, ich habe einen Beitrag tatsächlich nochmal erweitert.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Mathomat
Gast
|
 Mathomat Verfasst am: 23. Okt 2013 22:09 Titel: Mathomat Verfasst am: 23. Okt 2013 22:09 Titel: |
 |
|
| Zitat: | | Ich denke nicht, dass ein ^{-1} fehlt; wo soll das sein? |
..in der letzten Gleichung fehlts. ..Zumindest war's vorher mal da..
| Zitat: | | für reelle a1 und a2 tatsächlich |r| = 1; aber im allgemeinen Fall muss diese nicht der Fall sein. |
Stimmt schon, aber, dass a1 und a2 reell sind, ist hier ja der Fall.
Bleibt die Frage, was man von der anderen Lösung halten soll.!?
Und wie man heraus findet welche die richtige ist?! Dazu würde ich darauf hoffen, dass man z.B. für die Phase auf unterschiedlichen Wegen etwas anderes heraus bekommt, bei Kontrolle der falschen Lösung. Aber ein Beweis ist das auch nicht..
| Zitat: | | Quaternionen liefern lediglich eine andere (einfachere) Darstellung einer Drehung. |
Ach ja, da klingelt doch was: Quaternionen <-> Drehungen in 3D.
| Zitat: | | Sorry, ich habe einen Beitrag tatsächlich nochmal erweitert. |
Also wenn, dann sollte das Kritik im positivsten Sinne gewesen sein. Ist ja nicht so, als hätte ich was gegen mehr Informationen... |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 23. Okt 2013 23:21 Titel: TomS Verfasst am: 23. Okt 2013 23:21 Titel: |
 |
|
Bzgl. ^{-1} hast du recht, und ich hab's ergänzt.
Bzgl. des allgemeines Falles meine ich wirklich den allgemeinen Fall ;-) Wenn du eine Gleichung zu einem Polynom P(r) = 0 vom Grad N umformst, dann hat diese Gleichung immer genau N Lösungen, die i.A. komplex sind.
Betrachte z.B.
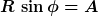
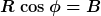
Die Lösung dieses Gleichungssystems ist im Reellen entweder genau ein Punkt oder kein Punkt. Durch Umformulieren in zwei Polynomgleichungen
 = 0)
mit i=1,2 jeweils vom Grad N=2 erhältst du für jede Gleichung exakt zwei Lösungen, die jedoch komplex sein können. Die weitere Einschränkung erfolgt zum einen über die Schnittmenge der beiden Lösungen, zum anderen über die Bedingung |r| = 1.
Die Darstellung mittels Quaternionen hat einen wesentlichen Vorteil, nämlich die einfache Darstellbarkeit einer Drehung um eine beliebige Achse. Aber sie kann die Geometrie einer Lösungsmenge eines Gleichungssystems nicht ändern.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Mathomat
Gast
|
 Mathomat Verfasst am: 24. Okt 2013 00:17 Titel: Mathomat Verfasst am: 24. Okt 2013 00:17 Titel: |
 |
|
| Zitat: | | Bzgl. des allgemeines Falles meine ich wirklich den allgemeinen Fall |
Hab ich ja alles nicht bezweifelt.. Auch die Anzahl der Lösungen in Abh. vom Polynom ist mir bekannt.
Das wird hier doch zum kleinen Problem... Eine Lösung reicht eigentlich..
Was meinst du mit der "Geometrie einer Lösungsmenge" ?? ..Einfach eine Lösungsmenge?!  |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 24. Okt 2013 00:30 Titel: TomS Verfasst am: 24. Okt 2013 00:30 Titel: |
 |
|
| Mathomat hat Folgendes geschrieben: | | Das wird hier doch zum kleinen Problem... Eine Lösung reicht eigentlich.. |
Ich bin mir nicht sicher, ob du die Idee verstanden hast. Wir starten mit zwei Polynomen und finden jeweils zwei i.A. komplexe Lösungen für phi. Das ergibt insgs. vier reelle Zahlen. Dann setzen wir beide Lösungen gleich, da es sich um das selbe phi handelt. Damit verbleibt noch (maximal) eine komplexe Lösung, also zwei reelle Zahlen. Die Bedingung |r|=1 reduziert dies auf (maximal) eine reelle Lösung.
Allein die Tatsache, dass du an der Polynomgleichung P(r) = 0 die Anzahl der Lösungen ablesen kannst ist ein Fortschritt.
| Mathomat hat Folgendes geschrieben: | | Was meinst du mit der "Geometrie einer Lösungsmenge" ?? ..Einfach eine Lösungsmenge?! ;) |
Nun, im obigen Fall kann ich die Lösungsmenge entweder mittels eines (reellen) Winkels phi beschreiben, oder mittels einer komplexen Zahl r plus Nebenbedingungen. Aber die Geometrie der Lösung wird durch diese Koordinatenwahl nicht geändert. Ein Kreis ist ein Kreis, ob ich ihn nun durch die eine Variable oder eine andere beschreibe.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Mathomat
Gast
|
 Mathomat Verfasst am: 24. Okt 2013 18:59 Titel: Mathomat Verfasst am: 24. Okt 2013 18:59 Titel: |
 |
|
Ich bin mir nicht sicher, ob du mich richtig verstanden hast..
..Wir starten eben nicht mit 2 Polynomen.
Wir starten als Physiker mit reellen Funktionen und Argumenten. Dann macht der Mathematiker in uns daraus eine komplexe Gleichung, und daraus ein (1) Polynom.
Jetzt bleiben wir im komplexen, bzw. lassen r stehen.
Für r gibt es 2 Lösungen.
Beide erfüllen |r|=1.
Nur eine liefert letztlich die richtigen Argumente. Und zwar Physiker-Argumente.
| Zitat: | | Allein die Tatsache, dass du an der Polynomgleichung P(r) = 0 die Anzahl der Lösungen ablesen kannst ist ein Fortschritt. |
Was soll das jetzt werden?! Das kann ich auch:
Bla-bla, für dich vielleicht.
Ich glaube wirklich, dass du mich nicht verstanden hast. Das würde auch erklären, warum du immer irgendetwas rechnest, evtl auch doppelt, nachdem ich garnicht gefragt hatte. Oder aufhörst, wenn's interessant wird.
Kann man nachen, muss man aber nicht, zumindest wenn's nach mir geht.
| Zitat: | | Aber die Geometrie der Lösung wird durch diese Koordinatenwahl nicht geändert. |
Geometrie?! "Landmessung" ?! Wenn da wenigstens noch das Wort "abstrakt" auftauchte...
Eine Lösung ist letztendlich eine Zahl. Und wenn du eine Zahl auf unterschiedliche Weise berechnest, bleibt es doch die gleiche Zahl.
Daher ist es schwachsinn von Geometrie zu sprechen. Eine identische Lösungsmenge. Fertig.
Und immer dran denken: R ist in C enthalten... |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 24. Okt 2013 19:32 Titel: TomS Verfasst am: 24. Okt 2013 19:32 Titel: |
 |
|
Evtl. hilft es, wenn du deine Problemstellungen, also explizite Gleichungen und Gleichungssysteme mal in einem Beitrag zusammenfasst. Bisher habe ich versucht, dein eigtl. Problem herauszufinden, was mir offensichtlich nicht gelingt.
Du bist nicht wirklich ernsthaft daran interessiert, den allgemeinen Fall zu verstehen. Für einen einfachen Fall mit einer Gleichung brauchst du aber kein Forum, da reicht eine Formelsammmlung. Der allgemeine Fall mehrerer Gleichungen in mehreren Koordinaten (den du zu Beginn eingeführt hast, nicht ich) kannst du nur über den Umweg über allgemeine (komplexe) Polynome verstehen.
Ist nicht böse gemeint, ich möchte nur vermeiden, dass ich weiterhin Fragen beantworte, die du nicht hast, und andere Fragen nicht beantworte, die dich eigtl. interessieren.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
j1
Gast
|
 j1 Verfasst am: 25. Okt 2013 20:19 Titel: j1 Verfasst am: 25. Okt 2013 20:19 Titel: |
 |
|
|
könnte hier der Satz impliziten Funktion weiter helfen? |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 25. Okt 2013 21:59 Titel: TomS Verfasst am: 25. Okt 2013 21:59 Titel: |
 |
|
noch ein Rätsel
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
|
|
















