| Autor |
Nachricht |
Stolperstein
Anmeldungsdatum: 15.04.2013
Beiträge: 70
Wohnort: Erfurt
|
 Stolperstein Verfasst am: 18. Aug 2013 15:17 Titel: Geschwindigkeit Stolperstein Verfasst am: 18. Aug 2013 15:17 Titel: Geschwindigkeit |
 |
|
Ich habe nur eine Frage:
Wie messt Ihr die Geschwindigkeit |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8581
|
 jh8979 Verfasst am: 18. Aug 2013 16:31 Titel: Re: Geschwindigkeit jh8979 Verfasst am: 18. Aug 2013 16:31 Titel: Re: Geschwindigkeit |
 |
|
| Stolperstein hat Folgendes geschrieben: | | Wie messt Ihr die Geschwindigkeit |
Wir sind anscheinend vom Physik-Niveau her irgendwo in der Grundschule angekommen... obwohl.. vermutlich verstehen dies selbst Kinder im Kindergarten schon...
http://de.wikipedia.org/wiki/Geschwindigkeit |
|
 |
Stolperstein
Anmeldungsdatum: 15.04.2013
Beiträge: 70
Wohnort: Erfurt
|
 Stolperstein Verfasst am: 18. Aug 2013 17:39 Titel: Geschwindigkeit Stolperstein Verfasst am: 18. Aug 2013 17:39 Titel: Geschwindigkeit |
 |
|
Wenn Du meinst, dies sei Kinderkram, so muss ich feststellen, dass mit der Beantwortung dieser Frage die Relativitaetstheorie steht oder faellt.
Nach Wiki ist die Geschwindigkeit die Aenderung des Ortes nach der Zeit.
Wenn ich also einen bestimmten Ort aufsuche, so lege ich eine Wegstrecke in einer Zeit zuruck.
Komme ich von einem anderem Ort, so aendert sich die Geschwindigkeit nach Betrag und Richtung. Wie bitte, soll es eine Hoechstgeschwindigkeit geben, wo doch jeder beliebige Bezugspunkt Ausganspunkt sein kann.
Damit laesst sich jeder Masse im Raum jede beliebige Geschwindigkeit zuordnen. (Auch Ueberlichtgeschwindigkeit)
 |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8581
|
 jh8979 Verfasst am: 18. Aug 2013 18:55 Titel: jh8979 Verfasst am: 18. Aug 2013 18:55 Titel: |
 |
|
Bezüglich eines beliebigen Punktes können auch Überlichtgeschwindigkeiten auftreten. Bezüglich eines physikalischen Beobachters allerdings nicht.
Oder anders ausgedrückt: Ein beliebiger Punkt kann sich mit Überlichtgeschwindigkeiten bewegen, ein physikalisches Objekt hingegen nicht, z.B. der Schnittpunkt beim Papierschneiden, obwohl sich jedes Molekül der Schere und des Papier mit weniger als Lichtgeschwindigkeit bewegt.
Dies ist im übrigen keine Vorraussetzung für die SRT sondern folgt aus ihr, da beim Beschleunigen der Energiebedarf divergiert, wenn man sich der Lichtgeschwindigkeit nähert.... aber wieso versuch ich Dir das eigentlich zu erklären?  |
|
 |
DrStupid
Anmeldungsdatum: 07.10.2009
Beiträge: 5043
|
 DrStupid Verfasst am: 18. Aug 2013 21:36 Titel: Re: Geschwindigkeit DrStupid Verfasst am: 18. Aug 2013 21:36 Titel: Re: Geschwindigkeit |
 |
|
| Stolperstein hat Folgendes geschrieben: | | Damit laesst sich jeder Masse im Raum jede beliebige Geschwindigkeit zuordnen. (Auch Ueberlichtgeschwindigkeit) |
Rechne das doch mal an einem konkreten Beispiel vor, damit wir wissen was Du meinst. |
|
 |
Stolperstein
Anmeldungsdatum: 15.04.2013
Beiträge: 70
Wohnort: Erfurt
|
 Stolperstein Verfasst am: 20. Aug 2013 13:35 Titel: Die Relativitaet der Gescgwindigkeit Stolperstein Verfasst am: 20. Aug 2013 13:35 Titel: Die Relativitaet der Gescgwindigkeit |
 |
|
Dr.Stubid
| Zitat: | | Rechne das doch mal an einem konkreten Beispiel vor, damit wir wissen was Du meinst. |
Ich sitze im Zug. Der Zug faehrt mit 80 km/h. Dies ist die Geschwindigkeit gegenueber dem Gleis.
Gegenueber einem anderen Zug, der mir entgegenkommt und der auch 80 km/h faehrt, habe ich 160 km/h.
Gegenueber dem Fligzeug, welches meinen Weg kreuzt, ergeben sich ca. 700 km/h.
Gegenueber der IIS weist mein Sitzplatz ca 8 km/s auf.
Du siehst, einem Gegenstand laesst sich jede beliebige Geschwindigkeit zuordnen.[/quote] |
|
 |
Jayk
Anmeldungsdatum: 22.08.2008
Beiträge: 1450
|
 Jayk Verfasst am: 20. Aug 2013 15:05 Titel: Jayk Verfasst am: 20. Aug 2013 15:05 Titel: |
 |
|
Die Geschwindigkeit ist  , fertig. Was du sagst, gilt bei Annahme eines absoluten Raums und einer absoluten Zeit. Wobei das auch nicht gerade sauber formuliert ist. Tatsache ist, dass nach der newtonschen Mechanik immer ein Bezugssystem gefunden werden kann, in dem irgendein Körper irgendeine Geschwindigkeit hat. , fertig. Was du sagst, gilt bei Annahme eines absoluten Raums und einer absoluten Zeit. Wobei das auch nicht gerade sauber formuliert ist. Tatsache ist, dass nach der newtonschen Mechanik immer ein Bezugssystem gefunden werden kann, in dem irgendein Körper irgendeine Geschwindigkeit hat.
In der SRT sind Raum und Zeit nicht absolut, sondern etwas, was in einem Inertialsystem eine bestimmte Länge hat, erscheint in einem anderen Inertialsystem länger oder kürzer, selbiges gilt für die Zeit. Aus der Lorentztransformation ergibt sich dann das einsteinsche Additionstheorem der Geschwindigkeiten, was nicht mehr beliebige Geschwindigkeiten zulässt.
Was mich sehr wundert: Du argumentierst in deiner Abhandlung Teil 1 (wann kommt denn nun Teil 3?) mit den Maxwellgleichungen. Ist dir eigentlich bewusst, dass diese ihre Form unter Lorentztransformationen beibehalten? Diese mathematische Tatsache hat Lorentz herausgefunden, bevor Einstein die Relativitätstheorie postulierte. |
|
 |
DrStupid
Anmeldungsdatum: 07.10.2009
Beiträge: 5043
|
 DrStupid Verfasst am: 20. Aug 2013 19:40 Titel: Re: Die Relativitaet der Gescgwindigkeit DrStupid Verfasst am: 20. Aug 2013 19:40 Titel: Re: Die Relativitaet der Gescgwindigkeit |
 |
|
| Stolperstein hat Folgendes geschrieben: | Ich sitze im Zug. Der Zug faehrt mit 80 km/h. Dies ist die Geschwindigkeit gegenueber dem Gleis.
Gegenueber einem anderen Zug, der mir entgegenkommt und der auch 80 km/h faehrt, habe ich 160 km/h. [...]
Du siehst, einem Gegenstand laesst sich jede beliebige Geschwindigkeit zuordnen. |
Ich sehe erst einmal nur, dass die Geschwindigkeit bezugssystemabhängig ist. Das ist trivial. Warum sich einem Gegenstand jede beliebige Geschwindigkeit zuordnen lässt, kann ich nicht erkennen. |
|
 |
Jayk
Anmeldungsdatum: 22.08.2008
Beiträge: 1450
|
 Jayk Verfasst am: 21. Aug 2013 21:14 Titel: Jayk Verfasst am: 21. Aug 2013 21:14 Titel: |
 |
|
In der klassischen, newtonschen Mechanik sind alle Inertialsysteme gleichberechtigt (sind sie ja auch in der SRT). Die Transformationen zwischen Inertialsystemen sind Galileitransformationen, welche eine Gruppenstruktur (die Galileigruppe) bilden. Die Elementartypen sind: Verschiebung des Nullpunkts im Galileiraum (d.h. Zeitnullpunkt und Koordinatenursprung) um eine Konstante (wegen Homogenität)  = (\vec x + \vec s, t + s)) , gleichförmige Bewegung , gleichförmige Bewegung  = (\vec x + \vec u t, t)) und Drehung des Raums (wegen Isotropie) und Drehung des Raums (wegen Isotropie)  = (G \vec x, t); G^T G = I) . Die Transformation erfolgt eindeutig durch Hintereinanderschaltung dieser Elementartransformationen. Die allgemeine Transformation mit eindeutig bestimmten Parametern ist also . Die Transformation erfolgt eindeutig durch Hintereinanderschaltung dieser Elementartransformationen. Die allgemeine Transformation mit eindeutig bestimmten Parametern ist also
 = (G \vec x + \vec s + \vec u t + \vec u s, t + s))

Und da es in der newtonschen Mechanik keine weiteren Beschränkungen für Geschwindigkeiten sind (außer, dass sie Elemente des R³ sind), die Addition von Vektoren aber selbst eine Gruppe bilden und als solche die Vollständigkeit erfüllen, kann ich also aus jedem Geschwindigkeitsvektor durch Addition eines bestimmten anderen Vektors jeden beliebigen anderen Vektor erhalten. In der SRT geht das im Prinzip genauso, nur eben nicht mit Galileitransformationen und unter der Maßgabe  für alle Geschwindigkeiten. Wenn ich einen Massenpunkt habe, der sich in einem Inertialsystem mit so einer Geschwindigkeit bewegt, dann kann ich durch Transformation in ein anderes Inertialsystem, das sich gegenüber diesem mit einer anderen Geschwindigkeit in diesem Bereich bewegt, jede beliebige andere Geschwindigkeit in diesem Bereich erhalten. Lediglich Lichtgeschwindigkeit selbst nimmt da eine Ausnahmerolle ein. für alle Geschwindigkeiten. Wenn ich einen Massenpunkt habe, der sich in einem Inertialsystem mit so einer Geschwindigkeit bewegt, dann kann ich durch Transformation in ein anderes Inertialsystem, das sich gegenüber diesem mit einer anderen Geschwindigkeit in diesem Bereich bewegt, jede beliebige andere Geschwindigkeit in diesem Bereich erhalten. Lediglich Lichtgeschwindigkeit selbst nimmt da eine Ausnahmerolle ein. |
|
 |
Stolperstein
Anmeldungsdatum: 15.04.2013
Beiträge: 70
Wohnort: Erfurt
|
 Stolperstein Verfasst am: 23. Aug 2013 11:15 Titel: Ausnahme Lichtgeschwindigkeit Stolperstein Verfasst am: 23. Aug 2013 11:15 Titel: Ausnahme Lichtgeschwindigkeit |
 |
|
Jayk
| Zitat: | | Wenn ich einen Massenpunkt habe, der sich in einem Inertialsystem mit so einer Geschwindigkeit bewegt, dann kann ich durch Transformation in ein anderes Inertialsystem, das sich gegenüber diesem mit einer anderen Geschwindigkeit in diesem Bereich bewegt, jede beliebige andere Geschwindigkeit in diesem Bereich erhalten. |
Voellig richtig
| Zitat: | | Lediglich Lichtgeschwindigkeit selbst nimmt da eine Ausnahmerolle ein. |
Wieso |
|
 |
DrStupid
Anmeldungsdatum: 07.10.2009
Beiträge: 5043
|
 DrStupid Verfasst am: 23. Aug 2013 18:06 Titel: Re: Ausnahme Lichtgeschwindigkeit DrStupid Verfasst am: 23. Aug 2013 18:06 Titel: Re: Ausnahme Lichtgeschwindigkeit |
 |
|
| Stolperstein hat Folgendes geschrieben: | | Zitat: | | Lediglich Lichtgeschwindigkeit selbst nimmt da eine Ausnahmerolle ein. |
Wieso |
Mit der Invarianz der Lichtgeschwindigkeit lassen sich diverse experimentelle Beobachtungen am einfachsten beschreiben. Deshalb hat Einstein diese Eigenschaft des Lichtes zum Postulat erhoben und diejenige Transformation ermittelt, die dazu passt. Dabei handelt es sich um die Lorentz-Transformation. |
|
 |
Jayk
Anmeldungsdatum: 22.08.2008
Beiträge: 1450
|
 Jayk Verfasst am: 23. Aug 2013 19:26 Titel: Re: Ausnahme Lichtgeschwindigkeit Jayk Verfasst am: 23. Aug 2013 19:26 Titel: Re: Ausnahme Lichtgeschwindigkeit |
 |
|
| Stolperstein hat Folgendes geschrieben: | Jayk
| Zitat: | | Wenn ich einen Massenpunkt habe, der sich in einem Inertialsystem mit so einer Geschwindigkeit bewegt, dann kann ich durch Transformation in ein anderes Inertialsystem, das sich gegenüber diesem mit einer anderen Geschwindigkeit in diesem Bereich bewegt, jede beliebige andere Geschwindigkeit in diesem Bereich erhalten. |
Voellig richtig
| Zitat: | | Lediglich Lichtgeschwindigkeit selbst nimmt da eine Ausnahmerolle ein. |
Wieso |
Aus algebraischen Gründen: Kann man eine Division durch null umkehren? Was wir hier gerade machen, sind ohnehin bloß mathematische Spielereien. 
Nimm dir eine Lorentztransformation vor:
 \\ ct' = \gamma (ct + \beta x') \end{array} \right.)
mit  , wobei u die Geschwindigkeit des neuen Bezugssystems relativ zum jetzigen (ungestrichenen) ist. Jetzt kann man , wobei u die Geschwindigkeit des neuen Bezugssystems relativ zum jetzigen (ungestrichenen) ist. Jetzt kann man 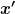 nach nach 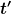 ableiten und die Geschwindigkeit im neuen System erhalten: ableiten und die Geschwindigkeit im neuen System erhalten:

Was im Grenzfall (Nenner -> 1) eine Galileitransformation ist. Wenn  ist, ist der Nenner undefiniert, wie du siehst. Das ist die Ausnahme, die ich meinte. Ansonsten gibt es keine weiteren Ausnahmen. Wenn du irgendeine Geschwindigkeit ist, ist der Nenner undefiniert, wie du siehst. Das ist die Ausnahme, die ich meinte. Ansonsten gibt es keine weiteren Ausnahmen. Wenn du irgendeine Geschwindigkeit  hast und stattdessen lieber hast und stattdessen lieber  mit mit  hättest, brauchst du nur ein Inertialsystem zu nehmen, das sich relativ dazu mit hättest, brauchst du nur ein Inertialsystem zu nehmen, das sich relativ dazu mit

bewegt, zu nehmen. Wenn du von Lichtgeschwindigkeit auf Lichtgeschwindigkeit kommen möchtest (mit demselben Vorzeichen), ist der Ausdruck undefiniert. Durch null kann alles sein, und tatsächlich bleibt Lichtgeschwindigkeit immer Lichtgeschwindigkeit, wie du an der Gleichung oben sehen kannst. Sie heißt übrigens Einsteinsches/relativistisches Additionstheorem für Geschwindigkeiten: http://de.wikipedia.org/wiki/Relativistisches_Additionstheorem_f%C3%BCr_Geschwindigkeiten |
|
 |
|


















