| Autor |
Nachricht |
DerVonNebenan
Anmeldungsdatum: 15.07.2012
Beiträge: 12
|
 DerVonNebenan Verfasst am: 15. Jul 2012 20:05 Titel: Übergang vom Orts- in den Impulsraum |
 |
|
Hallo,
ich befasse mich grad mit der Arbeit "http://wenku.baidu.com/view/6e34ac1ffc4ffe473368ab5a.html###" (Seite 132/133), in dem es um die Beschreibung von der quadratischen Dispersion von "flexual" Moden in einer Membran geht.
Die genaue Frage wäre dabei erstmal, wie man von der Gleichung (126) auf die Gleichung (129) kommt?
Wie wird der Nabla-Operator vom Orts- in den Impuls-Raum transformiert?
In den theo. Festköperbüchern steht geschrieben, dass eine Funktion der Form  ) in den Impuls-Raum durch
^a} \int d^a \vec{k} f(\vec{k}) ) transformiert werden kann, wobei hier  für die Dimension steht.
Kann mir hier jemand helfen????
LG
|
|
 |
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18026
|
| TomS Verfasst am: 15. Jul 2012 20:24 Titel: |
|
|
Die Transformation vom Orts- in den Impulsraum ist gegeben durch die Fouriertransformation
 \to F(k) = \int_{-\infty}^{+\infty}dx\,e^{-ikx}\,f(x))
Für die Differentation gilt dann
 \to \int_{-\infty}^{+\infty}dx\,e^{-ikx}\,\partial_x\,f(x) = -\int_{-\infty}^{+\infty}dx\,\left(\partial_x\,e^{-ikx}\right)\,f(x) = -\int_{-\infty}^{+\infty}dx\,\left(-ik\,e^{-ikx}\right)\,f(x) = ik\int_{-\infty}^{+\infty}dx\,e^{-ikx}\,f(x) = ik\,F(k))
In kartesischen Koordinaten kann man das sofort auf n Dimensionen und damit auch komponentenweise auf den Nablaoperator verallgemeinern.
Aber in der Festkörperphysik kommt oft noch die zusätzliche Eigenschaft der Periodizität im Ortsraum d.h. die Darstellung dieser Symmetrie im Impulsraum mittels der Blochwellen hinzu.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
Chillosaurus
Anmeldungsdatum: 07.08.2010
Beiträge: 2440
|
| Chillosaurus Verfasst am: 15. Jul 2012 20:29 Titel: Re: Übergang vom Orts- in den Impulsraum |
|
|
| DerVonNebenan hat Folgendes geschrieben: | Hallo,
ich befasse mich grad mit der Arbeit "http://wenku.baidu.com/view/6e34ac1ffc4ffe473368ab5a.html###" (Seite 132/133),
|
Das ist ja asiatisch.
| Zitat: | [...]
In den theo. Festköperbüchern steht geschrieben, dass eine Funktion der Form in den Impuls-Raum durch
transformiert werden kann, wobei hier für die Dimension steht.
[...] |
Das steht da gewiss nicht, da die Funktion f in beiden Fällen Funktion des Impulses k ist.
Von der Orts- in die Impulsdarstellung kommt man mit einer Fourier-Transformation.
|
|
|
DerVonNebenan
Anmeldungsdatum: 15.07.2012
Beiträge: 12
|
| DerVonNebenan Verfasst am: 15. Jul 2012 21:09 Titel: |
|
|
Hallo,
habe ich eben bei meiner Rechnung auch gesehen, dass die genannte Transformation von mir so nicht stimmt. Diese habe ich aus meiner Vorlesung. In den Büchern steht natürlich das richtig (habe wohl was falsch abgeschrieben).
Wenn nun sich
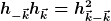
das so schreiben lässt, dann dürfte ich es richtig berechnet haben.
Nun wird ja diese kanonische Quantisierung mit dem Kommutatur betrachtet. Wie wird daraus nun der angebene Hamiltonian konstruiert?
LG
edit: Sorry, dass ich die asiatische Seite hier angeben habe. Von zu Hause kann ich keine Veröffnetlichungen runtenladen und habe diese genannte Seite oben bei google gefunden.
|
|
|
DerVonNebenan
Anmeldungsdatum: 15.07.2012
Beiträge: 12
|
| DerVonNebenan Verfasst am: 20. Jul 2012 18:19 Titel: |
|
|
Hallo,
ich bin nun dabei, aus der Heisenberg-Gleichung die angebene Dispersions zu bestimmen:
 , da der Ortsoperator mit sich selber kommutiert.
Zusammengefasst ergibt sich also:
Meine Frage wäre nun, wie ich diese Gleichung lösen kann, damit ich auf die angebene Dispersion komme?
LG
|
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18026
|
| TomS Verfasst am: 20. Jul 2012 19:21 Titel: |
|
|
Ohne dass du uns verrätst, wie die Operatoren definiert sind und was sie bedeuten, kann dir dabei niemand helfen
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
DerVonNebenan
Anmeldungsdatum: 15.07.2012
Beiträge: 12
|
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18026
|
| TomS Verfasst am: 20. Jul 2012 19:54 Titel: |
|
|
OK, so langsam sehe ich klarer.
Ich denke, zunächst hast du keine explizite Zeritabhängigkeit, d.h.
Dann sieht deine erste Bewegungsgleichung vernünftig aus; Hamiltonian quadratisch in P, d.h. Bewegungsgleichung linear in h. Du benötigst aber nochmals eine heisenbergsche Bewegungsleichung für P, die du analog ableitest.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
DerVonNebenan
Anmeldungsdatum: 15.07.2012
Beiträge: 12
|
| DerVonNebenan Verfasst am: 20. Jul 2012 20:00 Titel: |
|
|
Angeben ist  ) , was heißt, dass hier keine Zeitabhängigkeit drin steckt.
Die Frage wäre jetzt aber, warum benötigt man noch eine zweite Heisenberg-Gleichung?
Meinst du eine Gleichung für  und dann nochmal für  .
LG
|
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18026
|
| TomS Verfasst am: 20. Jul 2012 20:04 Titel: |
|
|
Man benötigt immer beide Gleichungen
für jeden Operator O eine; bei dir sind es unendlich viele P's und h's.
Rechne doch mal ein einfaches Beispiel zu warm werden, den harmonischen Oszillator:
)
d.h.
- die Bewegungsgleichung für x
- die Bewegungsgleichung für p
- die Lösung x(t), p(t)
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
DerVonNebenan
Anmeldungsdatum: 15.07.2012
Beiträge: 12
|
| DerVonNebenan Verfasst am: 20. Jul 2012 20:27 Titel: |
|
|
Okay. Habe das eine Rechnung für den QM-Oszillator gefunden.
Zusammen hätte ich dann:
Desweiteren wäre dann wohl hier  .
|
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18026
|
| TomS Verfasst am: 20. Jul 2012 20:29 Titel: |
|
|
Hast du die Bewegungsgleichung für den harmonischen Oszillator auch gelöst?
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
DerVonNebenan
Anmeldungsdatum: 15.07.2012
Beiträge: 12
|
| DerVonNebenan Verfasst am: 20. Jul 2012 20:32 Titel: |
|
|
Ich habe jetzt in einem Vorlesungsskript von mir die komplette Rechnung am harm. QM Oszillator gefunden. Denke, dass das somit dann klar ist. Muss nur nochmal verstehe, warum die beiden Heisenberg-Gleichungen quadriert werden =).
edit: Bräuchte doch nochmal kurz Hilfe
Wie wäre dann der weitere Weg, so dass ich zwei getrennte Gleichungen für den Ort und den Impuls bekomme, ohne Mischterme?
|
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18026
|
| TomS Verfasst am: 20. Jul 2012 21:35 Titel: |
|
|
Zwei Linearkombinationen wie beim harmonischen Oszillator sowie bestimmung der Koeffizienten der Linearkombinationen als Funktion von k?
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
DerVonNebenan
Anmeldungsdatum: 15.07.2012
Beiträge: 12
|
| DerVonNebenan Verfasst am: 20. Jul 2012 21:59 Titel: |
|
|
Mein Ansatz wäre nun einfach:
Ich möchte ja die Lösung für  haben. Daher schreibe ich das Ganze um in eine DGL 2. Ordnung:
Dann einfach dort oben einsezten und alles in ein Matheprogramm getippt, was die Lösung ausgibt.
Also müsste ich am Ende (indem ich den Impuls in der zweiten Gleichung umschreibe zu  ) folgende Gleichung lösen:
*edit: So ist nun gelöst und kommt auf die richtige Abhängigkeit.
|
|
|
|
Registrieren
Login
FAQ
Suchen
