| Autor |
Nachricht |
TruEnemy
Anmeldungsdatum: 01.11.2010
Beiträge: 516
|
 TruEnemy Verfasst am: 14. Mai 2012 16:55 Titel: Erwartungswerte |
 |
|
Hallo!
Meine Frage:
Es sei uns eine reellwertige Wellefunktion  ) gegeben. Es ist
zu zeigen, dass der Erwartungswert des Impulses  Null ist.
Mein Ansatz:
Für den Erwartungswert in Ortsdarstellung gilt wie folgt:
 \frac{\hbar}{i} \vec{\nabla} \psi (\vec{x},t) = \int d^3 x\;\psi (\vec{x},t) \frac{\hbar}{i} \vec{\nabla} \psi (\vec{x},t) \newline = \int d^3 x\; \frac{\hbar}{i} \vec{\nabla} \psi (\vec{x},t) \psi (\vec{x},t) = \int d^3 x\; \frac{\hbar}{i} \left( \vec{\nabla}\psi (\vec{x},t) \psi (\vec{x},t) + \psi (\vec{x},t) \vec{\nabla}\psi (\vec{x},t) \right))
Naja, weiter bin ich leider nicht gekommen, mir ist schleierhaft, wie das Null werden soll.
Wahrscheinlich ist aber schon der Ansatz falsch und man muss vielleicht die Darstellungs-
form der Wellefunktion ändern, d. h. z. B. die folgenden Darstellungswechsel verwenden?
 = \int d^3 p\;\frac{1}{\sqrt{(2 \pi \hbar)^3}}\;\widetilde{\psi}(\vec{p},t)\;e^{\frac{i \vec{p} \vec{x}}{\hbar}}\;,\;\widetilde{\psi}(\vec{p},t) = \int d^3 x\;\psi (\vec{x},t)\;e^{-\frac{i \vec{p} \vec{x}}{\hbar}})
Gruß. |
|
 |
Rmn
Anmeldungsdatum: 26.01.2010
Beiträge: 473
|
| Rmn Verfasst am: 14. Mai 2012 17:33 Titel: Re: Erwartungswerte |
|
|
 \frac{\hbar}{i} \vec{\nabla} \psi (\vec{x},t)=\frac{\hbar}{i} \int d^3 x\;\psi^* (\vec{x},t) \vec{\nabla} \psi (\vec{x},t))
Naja, alles was unter dem Integral steht ist reel, da die Wellenfunktion selbst reel ist. Multipliziert mit i ist der ganze Ausdruck rechts dann eine imaginäre Zahl. Erwartungswert von Impuls ist aber zwangsläufig reel. Was heißt das? |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18051
|
| TomS Verfasst am: 14. Mai 2012 19:46 Titel: |
|
|
Ja, die Antwort ist sehr einfach: der Erwartungswert einer Observablen muss reell sein. Im Falle einer rein reellwertigen Wellenfunktion kann aber das Integral nur rein imaginär oder Null sein. D.h. es bleibt nur die Null übrig.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
TruEnemy
Anmeldungsdatum: 01.11.2010
Beiträge: 516
|
| TruEnemy Verfasst am: 14. Mai 2012 20:54 Titel: |
|
|
 Stimmt, das hätte ich sehen müssen. Ich hätte in meiner Formel-Wut
einfach auch mal das  rausziehen sollen, dann wäre es wohl klar gewesen.
Nun soll gezeigt werden, dass, sofern die Fourier-Transformierte  ) der
Wellenfunktion reell ist, der Erwartungswert des Ortes  Null ist.
Für den Erwartungswert des Ortes gilt formell die folgende Relation:
 \;\vec{x}\; \psi (\vec{x},t) )
Nun muss ich aber wohl die Fourier-Darstellung von verwenden, oder?
 = \frac{1}{(2 \pi \hbar)^3} \int d^3 p\; \widetilde{\psi} (\vec{p},t) \; e^{i \vec{p} \vec{x} / \hbar} ) |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18051
|
| TomS Verfasst am: 14. Mai 2012 21:16 Titel: |
|
|
Nein, du sollst direkt die Wellenfunktion sowie den Ortsoperator in Impulsdarstellung benutzen. Den Zusammenhang mittels Fouriertransformation benötigst du nur, wenn du noch nicht weißt, wie der Ortsoperator in Impulsdarstellung aussieht.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
TruEnemy
Anmeldungsdatum: 01.11.2010
Beiträge: 516
|
| TruEnemy Verfasst am: 14. Mai 2012 21:23 Titel: |
|
|
Ja, die Impulsdarstellung des Ortsoperators hatten wir in der Vorlesung noch nicht.
Macht doch Sinn, hier die bereits oben erwähnte Darstellung zu nutzen, es wird ja in
der Aufgabe explizit darauf hingewiesen, dass die Fourier-Transformierte der Wellen-
funktion reellwertig ist. Also, so denke ich, sollte man dies auch anwenden!?? 
Vielleicht irre ich auch wieder, gut möglich  |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18051
|
| TomS Verfasst am: 14. Mai 2012 21:37 Titel: |
|
|
Du musst eigtl. nur verstehen, wie der Ortsoperator in Impulsdarstellung lautet. Zunächst gilt
 = p\,\psi(p))
d.h. der Impulsoperator wirkt als Multiplikation mit der Zahl p (vgl. Ortsoperator in Orstdarstellung)
Damit gilt sofort
\,p\,\psi(p))
und du benötigst die Definition der Wellenfuinktion im Impulsraum mittels der Fouriertransformation nicht.
Nun zum Ortsoperator: du kannst auf zwei Wegen verstehen, wie er in der Impulsdarstellung definiert ist. Zum einen kannst du dazu die Fouriertransformierte von
)
betrachten.
Zum zweiten kannst du einfach die kanonische Vertauschungsrelation
benutzen. In der Impulsdarstellung gilt
)
Den Kommutator kennst du, denn er ist unabhängig von der Darstellung. Hier wirkt er auf eine Wellenfunktion im Impulsraum. Den Orstoperator in der Impulsdarstellung (gekennzeichnet mit dem Index p) kannst du evtl. direkt erraten.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
TruEnemy
Anmeldungsdatum: 01.11.2010
Beiträge: 516
|
| TruEnemy Verfasst am: 14. Mai 2012 22:53 Titel: |
|
|
| TomS hat Folgendes geschrieben: | Du musst eigtl. nur verstehen, wie der Ortsoperator in Impulsdarstellung lautet. Zunächst gilt
d.h. der Impulsoperator wirkt als Multiplikation mit der Zahl p (vgl. Ortsoperator in Orstdarstellung)
Damit gilt sofort
|
Bis hier hin habe ich's verstanden. Sorry, das ist sicher alles richtig, aber wäre mein Weg denn so falsch?
 \;\vec{x}\; \psi (\vec{x},t)
<br />
& = \int d^3 x\; \left( \int d^3 p\;\frac{1}{\sqrt{(2 \pi \hbar)^3}}\;\widetilde{\psi}^* (\vec{p},t)\;e^{-i \vec{p} \vec{x}/\hbar} \right) \vec{x} \left( \int d^3 p\;\frac{1}{\sqrt{(2 \pi \hbar)^3}}\;\widetilde{\psi} (\vec{p},t)\;e^{i \vec{p} \vec{x}/\hbar} \right)
<br />
& = \left( \frac{1}{\sqrt{(2 \pi \hbar)^3}} \right)^2 \int d^3 x\;\underbrace{e^{-i \vec{p} \vec{x}/\hbar}\;e^{i \vec{p} \vec{x}/\hbar}}_{=\;1} \int d^3 p \int d^3 p\;\widetilde{\psi}^* (\vec{p},t) \;\vec{x}\; \widetilde{\psi} (\vec{p},t)
<br />
\end{split}
<br />
) |
|
|
Rmn
Anmeldungsdatum: 26.01.2010
Beiträge: 473
|
| Rmn Verfasst am: 14. Mai 2012 23:11 Titel: |
|
|
|
Die Integrationsvariable p ist in beiden Integralen verschieden. |
|
|
TruEnemy
Anmeldungsdatum: 01.11.2010
Beiträge: 516
|
| TruEnemy Verfasst am: 14. Mai 2012 23:29 Titel: |
|
|
Wie kann ich dann die vorletzte Zeile vereinfachen, also:
^3}} \right)^2}_{=:\;A} \int d^3 x\; \left( \int d^3 p\;\underbrace{\widetilde{\psi}^* (\vec{p},t)}_{=\;\widetilde{\psi}(\vec{p},t)}\;e^{-i \vec{p} \vec{x}/\hbar} \right) \vec{x} \Biggl( \int d^3 p\;\widetilde{\psi} (\vec{p},t)\;e^{i \vec{p} \vec{x}/\hbar} \Biggr) )
Ich denke mal, dass der folgende Schritt nicht richtig war?
_________________
'Dass ich erkenne, was die Welt im Innersten zusammenhält' Faust, Goethe |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18051
|
| TomS Verfasst am: 14. Mai 2012 23:46 Titel: |
|
|
Es ist unnötig kompliziert!
Du benötigst ausschließlich die Impulsdarstellung des Ortsoperators. Du benötigst zum Beweis selbst explizit nicht die Fouriertransformation!
Es genügt, die Definition des Ortsoperators in Impulsdarstellung zu verwenden und folgendes Integral zu betrachten:
\,\hat{x}_p\,\psi(p))
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
TruEnemy
Anmeldungsdatum: 01.11.2010
Beiträge: 516
|
| TruEnemy Verfasst am: 15. Mai 2012 06:40 Titel: |
|
|
Ich frag mal meinen Tutor, ob ich die Impulsdarstellung
des Ortsoperators verwenden darf. Aber mir stellt sich
dann sofort die Frage, welche Aussage sich über die
Wellenfunktion in Impulsdarstellung treffen lässt, wo
doch nur gegeben ist, dass die FT der Wellenfunktion
in Ortsdarstellung reellwertig ist.
_________________
'Dass ich erkenne, was die Welt im Innersten zusammenhält' Faust, Goethe |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18051
|
| TomS Verfasst am: 15. Mai 2012 06:49 Titel: |
|
|
| TruEnemy hat Folgendes geschrieben: | Nun soll gezeigt werden, dass, sofern die Fourier-Transformierte der
Wellenfunktion reell ist, der Erwartungswert des Ortes Null ist. |
In der Aufgabenstellung steht doch, dass die Fourier-Transformierte ... reell ist! Das ist die Impulsdarstellung!
Wie genau lautet denn die exakte Aufgabenstellung? Welche Funktion ist nun reell? Und welchen Zusammenhang zwischen Orts- und Impulsdarstellung für Wellenfunktioinen und Operatoren kennst du?
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
TruEnemy
Anmeldungsdatum: 01.11.2010
Beiträge: 516
|
| TruEnemy Verfasst am: 15. Mai 2012 09:16 Titel: |
|
|
Dein Zitat stellt inhaltlich schon die exakte Aufgabenstellung dar.
Mir war nicht wirklich bewusst, dass mit  ) bereits die
Impulsdarstellung der Wellenfunktion  ) gegeben ist. Es wurde in
der Vorlesung halt nicht explizit gesagt, dass man im Allgemeinen durch FT zwischen
den Darstellungen in verschiedenen Räumen wechseln kann. Ich habe mich bei der
Formel für den Erwartungswert immer an gehangen, von welcher
ich über das Skript die F-Dartsellung zur Hand hatte, in der dann
vorkommt, über die ich dann eine Aussage - nämlich dass sie reellwertig ist - treffen kann.
Zudem hatten wir auch weder den Ortsoperator in Impulsdarstellung noch die Formel für den
Orts-Erwartungswert im Impulsraum behandelt bzw. gegeben.
Im Internet meine ich gefunden zu haben, dass sich der Ortsoperator in Impulsdarstellung nur um das
Vorzeichen von dem Impulsoperator in Ortsdarstellung unterscheidet, somit müsste folgendes gelten:
_________________
'Dass ich erkenne, was die Welt im Innersten zusammenhält' Faust, Goethe |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18051
|
| TomS Verfasst am: 15. Mai 2012 10:18 Titel: |
|
|
Wichtig ist, dass du dir anhand des Kommutators bzw. der Eigenschaften der Fouriertransformation klar machst, warum das so ist.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
TruEnemy
Anmeldungsdatum: 01.11.2010
Beiträge: 516
|
| TruEnemy Verfasst am: 15. Mai 2012 14:04 Titel: |
|
|
Exakt, sorry, ich vergaß den Nabla-Operator (im dreidimensionalen Fall):
Zwischendurch mal ein dickes DANKE an alle, die mir hier helfen 
_{p} & = \int d^3 p\;\widetilde{\psi}^* (\vec{p},t) \left( \hat{\vec{x}} \right)_{p} \psi (\vec{p},t)
<br />
& = \int d^3 p\;\widetilde{\psi}^* (\vec{p},t)\; -\frac{\hbar}{i} \vec{\nabla}_{p}\; \psi (\vec{p},t)
<br />
& \stackrel{\mathrm{\widetilde{\psi}\;reell}}= -\frac{\hbar}{i} \int d^3 p\;\widetilde{\psi} (\vec{p},t)\; \vec{\nabla}_{p}\; \psi (\vec{p},t)
<br />
\end{split}
<br />
)
Damit ergibt sich zwangsläufig die selbe Argumentation wie vorher auch.
Nun fehlt mir noch das Hintergrundwissen, wie man auf den Ortsoperator
in der Impulsdarstellung kommt. Auffallend ist, dass sich diese Darstellung
von der Orts-Darstellung der Impulsoperators nur in dem Vorzeichen unter-
scheiden. Das kenne ich von der Kommutatorbeziehung  .
_________________
'Dass ich erkenne, was die Welt im Innersten zusammenhält' Faust, Goethe |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18051
|
| TomS Verfasst am: 15. Mai 2012 14:16 Titel: |
|
|
Also zum einen kannst du mit dem Kommutatror argumentieren. Wenn du die Ortsdarstellung (unter Anwendung der Produkteregel bei der Ableitung) kennst
= i\,\psi(x))
dann kannst du die Impulsdarstellung (ebenfalls unter Anwendung der Produktregel) eigtl. sofort ablesen:
= i\,\psi(p))
Andererseits kannst du die Eigenschaften der Fouriertransformation ausnutzen: http://de.wikipedia.org/wiki/Fourier-Transformation#Wichtige_Fourier-Transformations-Paare - darin die Nummer 6 in der ersten Tabelle. Man findet die Identität einfach durch partielle Integration
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
TruEnemy
Anmeldungsdatum: 01.11.2010
Beiträge: 516
|
| TruEnemy Verfasst am: 15. Mai 2012 22:07 Titel: |
|
|
Ich danke Dir, aber keine der beiden Herleitungen ist im Moment für mich nachvollziehbar.
Klar ist  ) , aber das Ergebnis sowie dessen Relevanz ist mir in
diesem Zusammenhang schleierhaft. Im zweiten Schritt machst Du im Prinzip dann das selbe.
Hier nimmst Du den Ortsoperator in der Impulsdarstellung aber schon als gegeben an?! Sorry.
_________________
'Dass ich erkenne, was die Welt im Innersten zusammenhält' Faust, Goethe |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18051
|
| TomS Verfasst am: 16. Mai 2012 08:03 Titel: |
|
|
Ich setze zunächst an, dass der Impulsoperator in Impulsdarstellung einfach als Zahl p wirkt, d.h.
 = p\,\psi(p))
Das ist ganz analog zum Ortsoperator in Ortsdarstellung,
 = x\,\psi(x))
der auch einfach einer Multiplikation der Wellenfunktion mit x enstpricht.
Dann setze ich
 = x\int_{-\infty}^{+\infty}dp\,e^{ipx}\,\psi(p) = \int_{-\infty}^{+\infty}dp\,x\,e^{ipx}\,\psi(p) = \int_{-\infty}^{+\infty}dp\,(-i\partial_p)\,e^{ipx}\,\psi(p) = \int_{-\infty}^{+\infty}dp\,e^{ipx}\,(i\partial_p)\,\psi(p))
Im letzten Schritt verwende ich partielle Integration.
Damit weiß ich, dass der Anwendung des Ortsoperators x auf die Wellenfunktion im Ortsraum (per Multiplikation mit x) eine einfache Entsprechung im Impulsraum hat, nämlich die Anwendung des Differentationsoperators. Das ist eine allgemeine Eigenschaft der Fouriertransformation und kann mathematisch exakt für die Fouriertransformation im Raum L² bewiesen werden.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
TruEnemy
Anmeldungsdatum: 01.11.2010
Beiträge: 516
|
| TruEnemy Verfasst am: 17. Mai 2012 19:22 Titel: |
|
|
Vielen Dank! Nun habe ich es verstanden  Bevor ich die Aufgabe angehe, die zeitabhängige Schrödinger-Gleichung
für herzuleiten, würde ich gern wissen, wie die grobe Vorgehensweise bei der folgenden Aufgabe aussieht:
http://s14.directupload.net/images/120517/abgtbjrp.png
Der Text verwirrt mich. Die Wellefunktion ist offensichtlich nur für  relevant, bei  ist sie nämlich Null.
Erster Schritt: Normierung durchführen, um die Normierungskonstante A zu haben, richtig? Anschließend berechnen:
 \; \frac{\hbar}{i} \frac{\partial}{\partial x} \; \psi (x) )
_________________
'Dass ich erkenne, was die Welt im Innersten zusammenhält' Faust, Goethe |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18051
|
| TomS Verfasst am: 17. Mai 2012 21:19 Titel: |
|
|
Korrekt.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
TruEnemy
Anmeldungsdatum: 01.11.2010
Beiträge: 516
|
| TruEnemy Verfasst am: 17. Mai 2012 21:27 Titel: |
|
|
Danke! Die Normierungsbedingung lautet dann also wie folgt?
|^2 \stackrel{\mathrm{!}}= 1 )
_________________
'Dass ich erkenne, was die Welt im Innersten zusammenhält' Faust, Goethe |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18051
|
| TomS Verfasst am: 17. Mai 2012 22:55 Titel: |
|
|
Genau
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
TruEnemy
Anmeldungsdatum: 01.11.2010
Beiträge: 516
|
| TruEnemy Verfasst am: 18. Mai 2012 14:25 Titel: |
|
|
 = A\;x\;e^{-\alpha x} )
|^2 = A^2\;x^2\;e^{-2\alpha x} )
|^2 = A^2 \int_{0}^{\infty}\;x^2\;e^{-2\alpha x} )
\;\text{normiert} = \sqrt{\frac{\alpha^3}{2}}\;x\;e^{-\alpha x} )
Ist das soweit richtig?
_________________
'Dass ich erkenne, was die Welt im Innersten zusammenhält' Faust, Goethe |
|
|
Gas140
Gast
|
| Gas140 Verfasst am: 18. Mai 2012 22:50 Titel: |
|
|
Hallo,
da ich zur Zeit am selben Blatt hocke und mir eure Diskussion über die Erwartungswerte sehr weitergeholfen haben, dachte ich kann auch mal ein wenig bei der a) helfen 
Für die Normierungskonstante komme ich auf 2 * a^(3/2).
Als nächstes musst du die Fouriertransformierte ausrechnen (wieder von 0 bis Infinity).
Grüße |
|
|
Gas140
Gast
|
| Gas140 Verfasst am: 19. Mai 2012 07:30 Titel: |
|
|
Guten Morgen,
Wobei ich mir nicht ganz sicher bin, sollte man nicht erst nach der FT im impulsraum normieren? |
|
|
TruEnemy
Anmeldungsdatum: 01.11.2010
Beiträge: 516
|
| TruEnemy Verfasst am: 19. Mai 2012 07:33 Titel: |
|
|
Sorry, aber wie kommst Du denn auf  ? Das ist für mich
nicht nachvollziehbar, meinen Rechenweg kannst Du ja oben sehen.
Wieso benötigt man die FT von  ) ? Du willst also den Erwartungs-
wert vom Impuls in der Impulsdarstellung ausrechnen? Klingt irgend-
wie logisch, da wir hier eine reellwertige Funktion haben und wir zuvor
ja gezeigt haben, dass dann der Erwartungswert des Impulses in der
Ortsdarstellung Null ist?!
_________________
'Dass ich erkenne, was die Welt im Innersten zusammenhält' Faust, Goethe |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18051
|
| TomS Verfasst am: 19. Mai 2012 07:37 Titel: |
|
|
Ich würde den Erwartungswert des Impulsoperators direkt in der Ortsdarstellung (= ohne Umweg über den Impulsraum und die Fouriertransformation) berechnen, das ist der direktere Weg. Dabei ist evtl. zu beachten, dass der Impulsoperator aufgrund der Randbedingung bei x=0 evtl. nicht selbstadjungiert ist!
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
TruEnemy
Anmeldungsdatum: 01.11.2010
Beiträge: 516
|
| TruEnemy Verfasst am: 19. Mai 2012 07:51 Titel: |
|
|
Ja, ich hätte ihn nun auch ohne Umwege in der Ortsdarstellung berechnet:
_{x} \; = \int d x\;\psi^* (x) \; \left(\frac{\hbar}{i} \frac{\partial}{\partial x} \; \psi (x)\right) = \frac{\hbar}{i} \int d x\;\psi^* (x) \; \left(\frac{\partial}{\partial x} \; \psi (x) \right) )
Aber mich verwirrt trotzdem der vorhin erwähnte, folgende Sachverhalt:
| Zitat: |
... da wir hier eine reellwertige Funktion haben und wir zuvor ja gezeigt haben,
dass dann der Erwartungswert des Impulses in der Ortsdarstellung Null ist?! |
_________________
'Dass ich erkenne, was die Welt im Innersten zusammenhält' Faust, Goethe |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18051
|
| TomS Verfasst am: 19. Mai 2012 08:17 Titel: |
|
|
Der Ausgangspunkt war folgende Aussage:
Der Erwartungswert einer Observablen muss reell sein.
Eine Observable entspricht aber einem selbstadjungierten Operator.
Der Impulsoperator ist aber auf dem Intervall [0,∞[ nicht selbstadjungiert!
Beweis
Setze
 = e^{ipx})
Dann ist
\,u_p(x) = p\,u_p(x))
und somit liegt eine Eigenfunktion zum Impulsoperator mit Eigenwert p vor.
Nun setzen wir p = i|k|.
Damit ist
 = e^{-|k|x} )
offensichtliche eine Eigenfunktion zum imaginären Eigenwert i|k|. Außerdem ist diese Funktion sicherlich quadratintegrierbar und damit Element des Hilbertraums L²[0,∞[.
Wir haben also einen Widerspruch zum reellwertigen Spektrum eines selbstadjungierten Operators konstruiert; somit kann der Impulsoperator auf dem o.g. Intervall nicht selbstadjungiert sein. ■
Und damit ist die o.g. Aussage Der Erwartungswert einer Observablen muss reell sein auf den hier vorliegenden Fall evtl. gar nicht anwendbar - d.h. man muss die Rechnung explizit durchführen!
Übrigens kann man sich im Falle reellwertiger Funktionen folgenden Sachverhalt zu Nutze machen
Damit sieht man sofort, warum im o.g. der Impulsoperator nicht selbstadjungiert ist (besser, da es sich um ein Matrixelement handelt: warum er nicht einmal symmetrisch ist): die Randterme bei x=a und x=b können die Symmetrie bzw. Selbstadjungiertheit zerstören.
Falls b gegen Unendlich geht muss die Wellenfunktion bei x=b verschwinden (auch das ist eigtl. eine 'Physiker-Argumentation' und man kann Gegenbeispiele finden ...). Aber wenn wie im vorliegenden Fall a einen endlichen Wert hat, dann muss dafür nicht zwingend die Randbedingung vorliegen, dass die Wellenfunktion bei x=a verschwindet.
Einen Knoten bei x=a erhält man für die eingespannte Saite d.h. das Teilchen im unendlich hohen Potentialtopf.
Im hier vorliegenden Fall liegt zufälligerweise ebenfalls eine Wellenfunktion vor, die dieser Randbedingung genügt, aber es ist nicht ersichtlich, dass nicht auch das von mir konstruierte Gegenbeispiel exp(-|k|x) zulässig wäre.
Generell gilt, dass die Eigenschaft, ob ein Operator selbstadjungiert ist, nicht nur vom Operator selbst bestimmt wird, sondern dass der Hilbertraum, hier L²[a,b] inkl. der Randbedingungen, also des Definitionsbereiches des Operators, eine entscheidende Rolle spielt.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago.
Zuletzt bearbeitet von TomS am 19. Mai 2012 09:23, insgesamt einmal bearbeitet |
|
|
TruEnemy
Anmeldungsdatum: 01.11.2010
Beiträge: 516
|
| TruEnemy Verfasst am: 19. Mai 2012 17:35 Titel: |
|
|
Viel zu verdauen. Bitte nicht böse sein, wenn nun einige Fragen kommen.
| Zitat: | Der Erwartungswert einer Observablen muss reell sein.
Eine Observable entspricht aber einem selbstadjungierten Operator.
Der Impulsoperator ist aber auf dem Intervall [0,∞[ nicht selbstadjungiert! |
Hieraus folgere ich: wenn der Impulsoperator auf dem zu betrachtenden
Intervall nicht mehr selbstadjungiert ist, so ist er auch keine Observable,
und der Erwartungswert des Impulsoperators auf diesem Intervall kann
komplex sein, wobei von diesem aber nur der Realteil physikalisch rele-vant ist?
_{x} \; = \int_{0}^{\infty} d x\;\psi^* (x) \; \frac{\hbar}{i} \frac{\partial}{\partial x} \; \psi (x) = \frac{\hbar}{i} \int_{0}^{\infty} d x\;\psi (x) \; \frac{\partial}{\partial x} \; \psi (x) )
 \; \frac{\partial}{\partial x} \; \psi (x) = \int_{0}^{\infty} dx\;\frac{1}{2} \frac{\partial}{\partial x} \psi^2 (x) = \frac{1}{2} \psi^2 (x)|_{0}^{\infty} )
_{x} \; = \frac{\hbar}{2i} \psi^2 (x)|_{0}^{\infty} = \frac{\hbar}{2i} \psi^2 (x \rightarrow \infty) - \frac{\hbar}{2i} \psi^2 (x = 0) )
Wobei ich mir überhaupt nicht sicher bin, ob der letzte Schritt machbar ist.
Wahrsch. habe ich mir die folgenden Aussagen nicht richtig zu Nutze gemacht:
| Zitat: |
Falls b gegen Unendlich geht muss die Wellenfunktion bei x=b verschwinden ...
|
Tut sie, sie wird Null!(?)
| Zitat: |
Einen Knoten bei x=a erhält man für die eingespannte Saite d.h. das Teilchen
im unendlich hohen Potentialtopf. Im hier vorliegenden Fall liegt zufälligerweise
ebenfalls eine Wellenfunktion vor, die dieser Randbedingung genügt
|
...
_________________
'Dass ich erkenne, was die Welt im Innersten zusammenhält' Faust, Goethe |
|
|
Gas140
Gast
|
| Gas140 Verfasst am: 19. Mai 2012 21:25 Titel: |
|
|
| TruEnemy hat Folgendes geschrieben: | Sorry, aber wie kommst Du denn auf ? Das ist für mich
nicht nachvollziehbar, meinen Rechenweg kannst Du ja oben sehen.
Wieso benötigt man die FT von ? Du willst also den Erwartungs-
wert vom Impuls in der Impulsdarstellung ausrechnen? Klingt irgend-
wie logisch, da wir hier eine reellwertige Funktion haben und wir zuvor
ja gezeigt haben, dass dann der Erwartungswert des Impulses in der
Ortsdarstellung Null ist?! |
Hallo,
Mit der FT komme ich anachließend genau auf das Integral was als Hinweis angegeben ist.
Viele Grüße |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18051
|
| TomS Verfasst am: 19. Mai 2012 21:37 Titel: |
|
|
@TrueEnemy: du hast mit deiner Rechnung völlig recht.
Üblicherweise nimmt man an, dass Wellenfunktionen "aus physikalischen Gründen" im Unendlichen verschwinden. Mathematisch ist das für den L²-Hilbertraum bzw. die Quadratintegrabilität aber nicht notwendig. Man kann z.B. eine Folge immer enger werdender Peaks konstruieren, so dass die Wellenfunktion im Unendlichen nicht verschwindet (bzw. keine Grenzwert hat) jedoch die Folge der durch die Peaks definierten Flächen endlich bleibt. Physikalisch ist das aber nicht sinnvoll.
Für x=a muss es einen physikalischen Grund geben, warum da ein Knoten sein soll. Ohne diesen Knoten ist der Operator wie diskutiert nicht selbstadjungiert.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago.
Zuletzt bearbeitet von TomS am 20. Mai 2012 07:14, insgesamt einmal bearbeitet |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18051
|
|
|
TruEnemy
Anmeldungsdatum: 01.11.2010
Beiträge: 516
|
| TruEnemy Verfasst am: 20. Mai 2012 10:49 Titel: |
|
|
Deine vorletzte Antwort habe ich mehr oder minder verstanden, aber
bei Deiner zweiten Antwort weiß ich nicht, worauf Du dich beziehst.
 = A\;x\;e^{-\alpha x}\;,\;A = \sqrt{\frac{\alpha^3}{2}}\;,\; \Rightarrow \psi(x)\;\text{normiert} = \sqrt{\frac{\alpha^3}{2}}\;x\;e^{-\alpha x} )
Ich hoffe einfach mal, dass meine vorangegangene Normierungsrechnung
richtig ist, leider hat sie niemand kommentiert ^^ Ich erhälte dann also:
_{x} \; & = \frac{\hbar}{2i} \left(\sqrt{\frac{\alpha^3}{2}}\;x\;e^{-\alpha x}\right)_{x \rightarrow \infty}^2 - \frac{\hbar}{2i} \left(\sqrt{\frac{\alpha^3}{2}}\;x\;e^{-\alpha x}\right)_{x = 0}^2
<br />
& = \frac{\hbar}{2i} \frac{\alpha^3}{2}\;\underbrace{x^2\;e^{-2\alpha x}}_{\rightarrow 0\;\text{für}\;x \rightarrow \infty\;???} - \frac{\hbar}{2i} \frac{\alpha^3}{2}\;\underbrace{x^2\;e^{-2\alpha x}}_{???\;\text{für}\;x = 0}
<br />
\end{split}
<br />
)
Wie Ihr unschwer erkönnen könnt, habe ich da ein paar Probleme:
Dass  für  Eins ist, ist klar, aber  wäre Null und somit
alles Null? Das kann nicht sein ...
_________________
'Dass ich erkenne, was die Welt im Innersten zusammenhält' Faust, Goethe |
|
|
Gas140
Gast
|
| Gas140 Verfasst am: 20. Mai 2012 13:29 Titel: |
|
|
| TruEnemy hat Folgendes geschrieben: |
Ich hoffe einfach mal, dass meine vorangegangene Normierungsrechnung
richtig ist, leider hat sie niemand kommentiert ^^ Ich erhälte dann also:
|
Hallo,
bei meiner Normierung erhalte ich immernoch 2*(a^3)^(1/2). Aber unterscheidet sich ja nur durch einen Vorfaktor, deswegen sollte es da keine Probleme geben.
Habe allerdings grad deine Rechnung angeschaut und da stimmt irgendwas nicht.
Wenn du -ax substituierst kommst du auf das richtige!
Grüße |
|
|
Friedi
Anmeldungsdatum: 06.05.2012
Beiträge: 30
|
| Friedi Verfasst am: 20. Mai 2012 14:28 Titel: |
|
|
normierung:
ist richtig.
dann muss man die fouriertransformierte berechnen richtig? kann mir jemand sagen, was dafür rauskommt? ich komm da irgendwie nur auf komisches zeugs
 = \frac{\sqrt{2\alpha^3}}{\sqrt{\pi}(\alpha+ik)^2}
<br />
)
das stimmt irgendwie nicht oder?
und dann muss doch
|^2
<br />
)
berechnen werden oder?
danke für die hilfe
Zuletzt bearbeitet von Friedi am 20. Mai 2012 15:19, insgesamt einmal bearbeitet |
|
|
Gas140
Gast
|
| Gas140 Verfasst am: 20. Mai 2012 14:31 Titel: |
|
|
| Friedi hat Folgendes geschrieben: | normierung:
<br />
)
ist richtig.
dann muss man die fouriertransformierte berechnen richtig? kann mir jemand sagen, was dafür rauskommt? ich komm da irgendwie nur auf komisches zeugs
 = \frac{\sqrt{2\alpha^3}}{\sqrt{\pi}(\alpha-ik)^2}
<br />
)
das stimmt irgendwie nicht oder?
und dann muss doch
berechnen oder?
danke für die hilfe |
Hallo,
die Fouriertransformierte stimmt (zumindest hab ich es auch so). Wenn du Psi*Psi berechnest bekommst du im Nenner (a^2+k^2)^2 und kannst den Hinweis vom Blatt benutzen.
Viele Grüße
Michael |
|
|
Friedi
Anmeldungsdatum: 06.05.2012
Beiträge: 30
|
| Friedi Verfasst am: 20. Mai 2012 14:38 Titel: |
|
|
cool danke!
eine andere frage noch: wie verschwindet dann das  ?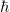
muss man das
durch was anderes ersetzen?
grüße
Friedi |
|
|
Gas140
Gast
|
| Gas140 Verfasst am: 20. Mai 2012 14:44 Titel: |
|
|
Hallo,
Da bin ich mir auch nicht 100% sicher, aber ich habe genau das Integral gerechnet was du gepostet hast.
Die a's haben sich bei mir rausgekürzt. Am Ende hatte ich nur etwas in Abhängigkeit von hquer.
An dem Punkt bin ich mir auch noch nicht ganz sicher ob ich einfach hquer einsetzen sollte, da ich damit auch einen ziemlich kleinen Zahlenwert herausbekomme (~10^-34).
Grüße
Michael |
|
|
|
Registrieren
Login
FAQ
Suchen
