| Autor |
Nachricht |
max_doering
Anmeldungsdatum: 13.03.2011
Beiträge: 50
|
 max_doering Verfasst am: 07. Jul 2011 19:12 Titel: Herleitung des relativistischen Impuls |
 |
|
Hallo,
habe ein kleines Problem bei der Herleitung des relativistischen Impuls.. Ich hatte mir das wie folgt überlegt:
Die Kraft wird beschrieben durch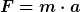 
Für hohe Geschwindigkeiten muss beachtet werden :  \cdot a)
Des weiteren gilt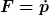 
Also gilt :
 \cdot \frac{dv}{dt} dt=\int m(v) dv = \int \frac{m_{0}}{\sqrt{1-\frac{v^2}{c^2}}}dv=m_{0}*c*arcsin(\frac{v}{c})+p_{0})
.. Wie man sieht komme ich nicht auf das gewünschte Ergebnis!
Es wäre sehr nett, wenn mir jemand sagen könnte, wo in meinen Überlegungen der Fehler steckt bzw. was ich falsch gemacht habe!
MfG. M.Döring |
|
 |
DrStupid
Anmeldungsdatum: 07.10.2009
Beiträge: 5041
|
| DrStupid Verfasst am: 07. Jul 2011 20:21 Titel: Re: Herleitung des relativistischen Impuls |
|
|
| max_doering hat Folgendes geschrieben: | | Die Kraft wird beschrieben durch |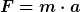
Das gilt nur wenn m konstant ist.
| max_doering hat Folgendes geschrieben: | | Für hohe Geschwindigkeiten muss beachtet werden : |
Ganz im Gegenteil. Das darf man nicht machen, weil F=m·a nicht mehr gilt, wenn die Masse nicht konstant ist.
Da Du die Geschwindigkeitsabhängigkeit der trägen Masse bereits kennst, ist die Sache viel einfacher. Du musst sie nur in die Impulsdefinition p = m·v einsetzen und fertig. Die eigentliche Herausforderung besteht darin, m(v) zu finden. |
|
|
max_doering
Anmeldungsdatum: 13.03.2011
Beiträge: 50
|
| max_doering Verfasst am: 07. Jul 2011 22:38 Titel: |
|
|
ah ok, ich verstehe!
Habe jetzt mal ein wenig rumprobiert, und bin auf folgenden "korrigierten" Kraftansatz gekommen:
mit
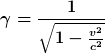
... scheint mir ein wenig komisch.. stimmt das? |
|
|
DrStupid
Anmeldungsdatum: 07.10.2009
Beiträge: 5041
|
| DrStupid Verfasst am: 07. Jul 2011 22:59 Titel: |
|
|
| max_doering hat Folgendes geschrieben: | Habe jetzt mal ein wenig rumprobiert, und bin auf folgenden "korrigierten" Kraftansatz gekommen:
mit
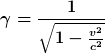
... scheint mir ein wenig komisch.. stimmt das? |
Das stimmt nur, wenn die Beschleunigung in Richtung der Geschwindigkeit erfolgt. Deshalb wird  gelegentlich auch als longitudinale Masse bezeichnet. Die allgemeine Gleichung sieht so aus:
}}{{c^2 - v^2 }}} \right] \cdot \gamma)
oder in Matrizenschreibweise
wobei I die Einheitsmatrix ist. |
|
|
max_doering
Anmeldungsdatum: 13.03.2011
Beiträge: 50
|
| max_doering Verfasst am: 12. Jul 2011 12:55 Titel: |
|
|
Oh ok. Danke für die Antworten!
Mich würde interessieren wie man auf die allgemeine Formel kommt!? Kennt jemand eine Herleitung bzw. weiß jemand, welchen Ansatz ich verwenden muss? |
|
|
VeryApe
Anmeldungsdatum: 10.02.2008
Beiträge: 3247
|
| VeryApe Verfasst am: 12. Jul 2011 14:10 Titel: |
|
|
Die Kraft ist definiert als die Impulsänderung pro zeit
F=\frac {dp}{dt}
p1=m*v
p2=(m+dm)* (v+dv) =m*v+dm*v+dv*m+dm*dv
der letzte Term ist unendlichklein zum Quadrat
Der zweite Term ist bekannt.
der heißt m*a der erste Term könntest du ebenfalls damit deuten in dem pro dt eineStückchen masse dm das Impulslos ist auf das Bezugssystem hinzu kommt und daher in der zeit dt auf v beschleunigt werden muß.
Die Masse wächst an mit impulslosen masse stückhen.
Das heißt dieses Stückchen wird anders beschleunigt und zwar mit einer unendlich großen beschleunigung, allerdings hört man das nicht gern in der Physik aufgrund der nicht wohl definierten Beschleunigung, die sich daraus ergibt das man die verflossene zeiteinheit nicht wohldefiniert sondern gegen null gehen lässt.
F=m*a1+ dm*a2
Die physikalische einwandfreie Formel ist aber diese hier
|
|
|
max_doering
Anmeldungsdatum: 13.03.2011
Beiträge: 50
|
| max_doering Verfasst am: 12. Jul 2011 17:27 Titel: |
|
|
ok, folgendes Beispiel:
Wenn ich das dann einsetze :
^{-\frac{3}{2}}+(1-\frac{v^2}{c^2})^{-\frac{1}{2}}] \\
<br />
=50 kg * \begin{bmatrix}
<br />
29\\3\\2
<br />
\end{bmatrix}\frac{m}{s^2} * [\frac{98}{100}*(1-\frac{98}{100})^{-\frac{3}{2}}+(1-\frac{98}{100})^{-\frac{1}{2}}] \\
<br />
=\begin{bmatrix}
<br />
512,6\\53
<br />
\\35,4\end{bmatrix}kN)
Kommt mir ein wenig komisch vor.. stimmt das so? |
|
|
VeryApe
Anmeldungsdatum: 10.02.2008
Beiträge: 3247
|
| VeryApe Verfasst am: 12. Jul 2011 19:45 Titel: |
|
|
Nein überleg nochmal was ist mit den Beschleunigungsrichtungen in denen die Geschwindigkeit null war.
wie siehts hier mit dm/dt * v aus. |
|
|
Systemdynamiker
Anmeldungsdatum: 22.10.2008
Beiträge: 594
Wohnort: Flurlingen
|
| Systemdynamiker Verfasst am: 18. Aug 2011 21:30 Titel: Impuls als Basis |
|
|
Die Herleitung der relativistischen Masse(Energie)-Impuls-Beziehung ist recht einfach, wenn man nicht von den Newtonmechanik ausgeht
http://www.youtube.com/watch?v=XK1xX2FwFMg
_________________
Herzliche Grüsse Werner Maurer |
|
|
DrStupid
Anmeldungsdatum: 07.10.2009
Beiträge: 5041
|
| DrStupid Verfasst am: 19. Aug 2011 15:40 Titel: Re: Impuls als Basis |
|
|
| Systemdynamiker hat Folgendes geschrieben: | Die Herleitung der relativistischen Masse(Energie)-Impuls-Beziehung ist recht einfach, wenn man nicht von den Newtonmechanik ausgeht
http://www.youtube.com/watch?v=XK1xX2FwFMg |
Die Verwendung der Einsteinschen Masse-Energieäquivalenz ist hier streng genommen nicht zulässig, weil Einstein sie nur für die Ruhemasse und die Ruheenergie hergeleitet hat. Hier geht es aber um die träge Masse. Dass die äquivalent zur Gesamtenergie ist, kann man zwar leicht nachweisen, wenn man ihre Geschwindigkeitsabhängigkeit kennt, aber genau die soll ja hergeleitet werden. So funktioniert das also nicht.
Da sich die SRT von der klassischen Mechanik nur durch die Transformation zwischen bewegten Bezugssystemen unterscheidet, gehe ich bei der Herleitung von der Newtonschen Dynamik aus (die ja unabhängig von der Transformation ist) und berechne dann, was daraus bei Galilei-Transformation und Lorentz-Transformation folgt.
Zunächst einmal schränke ich die möglichen Geschwindigkeitsabhängigkeiten sinnvoll ein. Um das Relativitätsprinzip und die Additivität von Impulsen zu gewährleisten, lege ich beispielsweise fest, dass alle trägen Massen in allen Bezugssystemen die gleiche Geschwindigkeitsabhängigkeit haben sollen. Das wird gewährleistet durch
 \quad m\left( v \right): = m_0 \cdot f\left( v \right))
wobei f(v) eine für alle Körper und alle Inertialsysteme gleiche Funktion der Geschwindigkeit und m0 eine für jeden Körper charakteristische, aber vom Bezugssystem unabhängige Ruhemasse ist. Daraus folgt schon mal
 \quad f\left( 0 \right) = 1)
Um Anisotropie zu gewährleisten muss sie zusätzlich richtungsunabhängig sein. Im eindimensionalen Fall (auf den ich mich hier beschränke) bedeutet das
 \quad f\left( { - v} \right) = f\left( v \right))
Zur Bestimmung der Geschwindigkeitsabhängigkeit konstruiere ich ein kleines Gedankenexperiment, bei dem im Bezugssystem K ein mit der Geschwindigkeit v bewegter Körper A vollständig unelastisch mit einem zunächst ruhenden Körper B kollidiert und das Kollisionsprodukt sich anschließend mit der Geschwindigkeit u weiterbewegt. Die Körper A und B haben beide die gleiche Ruhemasse m0. Das Kollisionsprodukt hat die Ruhemasse M0, von der ich nicht verlange, dass sie 2·m0 entsprechen muss. Für den Gesamtimpuls vor und nach dem Stoß gilt dann
 \quad p = m_0 \cdot f\left( v \right) \cdot v = M_0 \cdot f\left( u \right) \cdot u)
Jetzt wage ich einfach mal einen Schuss ins Blaue und vermute, dass träge Massen additiv sind. Natürlich weiß ich, dass das so ist, weil ich das Ergebnis bereits kenne, aber wenn ich es an dieser Stelle noch nicht wüsste, müsste ich es hier postulieren und anschließend prüfen, ob das Ergebnis diese Bedingung wirklich erfüllt. Damit gilt für die träge Masse des Kollisionsproduktes
 \quad M_0 \cdot f\left( u \right) = m_0 \cdot f\left( v \right) + m_0 \cdot f\left( 0 \right))
Zusammen mit (2) und (4) folgt daraus
 \quad f\left( v \right) = \frac{u}{{v - u}})
Ich brauche jetzt also nur noch die Geschwindigkeit u des Kollisionsproduktes und schon habe ich die gesuchte Geschwindigkeitsabhängigkeit. Dazu betrachte ich das Ganze in einem gegenüber K mit der Geschwindigkeit v bewegten Bezugssytem K’. Die Situation ist hier völlig symmetrisch. Es ändern sich nur die Vorzeichen. Der Körper B prallt also mit der Geschwindigkeit -v auf den zunächst ruhenden Körper A und das Kollisionsprodukt bewegt sich anschließend mit der Geschwindigkeit
 \quad u' = - u)
Wie es jetzt weitergeht, hängt von der Transformation ab:
Nach der in der klassischen mechanik gültigen Galilei-Transformation gilt
 \quad u' = - u = u - v)
Das ergibt mit (6)
 \quad f\left( v \right) = 1)
Im Rahmen der klassischen Mechanik ist die träge Masse also bezugssysteminvariant, was wohl niemanden sonderlich überraschen wird.
Beim Wechsel zur SRT wird die Galilei-Transformation durch die Lorentz-Transformation ersetzt. Daraus folgt für die Geschwindigkeit
 \quad u' = - u = \frac{{u - v}}{{1 - \frac{{u \cdot v}}{{c^2 }}}})
Zusammen mit (1) und (6) ergibt das die bekannte relativistische Geschwindigkeitsabhängigkeit der trägen Masse:
 \quad p = m \cdot v = \frac{{m_0 \cdot v}}{{\sqrt {1 - \frac{{v^2 }}{{c^2 }}} }})
Und weil die Geschwindigkeit da im Quadrat steht, gilt die nicht nur für den eindimensionalen Fall, für den ich sie hier hergeleitet habe, sondern auch im dreidimensionalen Raum.
Um meine obige Vermutung bezüglich der Additivität von trägen Massen zu prüfen, stelle ich nun eine Beziehung zu einer Größe her, von der ich weiß, dass sie additiv ist - nämlich der Energie. Wenn an einem geschlossenen System nur mechanische Arbeit verrichtet wird, ist die Änderung seiner Energie gleich der verrichteten Arbeit:
 \quad dE = dW = F \cdot ds = v \cdot dp)
Aus der Newtonschen Impulsdefinition und (11) folgt
 \quad p = m \cdot v = \frac{{m_0 \cdot v}}{{\sqrt {1 - \frac{{v^2 }}{{c^2 }}} }})
und daraus ergibt sich das Differential
 \quad dp = m \cdot dv + v \cdot dm = \frac{{m_0 \cdot \left[ {dv + \frac{{v \cdot \left( {v \cdot dv} \right)}}{{c^2 - v^2 }}} \right]}}{{\sqrt {1 - \frac{{v^2 }}{{c^2 }}} }} = m \cdot \left[ {dv + \frac{{v \cdot \left( {v \cdot dv} \right)}}{{c^2 - v^2 }}} \right])
zusammen mit (12) führt das zu überraschend einfachen Gleichung
 \quad dE = c^2 \cdot dm)
Die Integration ergibt zunächst
 \quad E = E_0 + \left( {m - m_0 } \right) \cdot c^2)
und mit der Äquivalenz von Ruhemasse und Ruheenergie (die Einstein schon freundlicherweise für mich hergeleitet hat) folgt schließlich die Äquivalenz von Energie und träger Masse:
 \quad E = m \cdot c^2)
Aus der bekannten Additivität der Energie
 \quad E_{ges} = \sum {E_i = } \sum {\left( {m_i \cdot c^2 } \right)} = \left( {\sum {m_i } } \right) \cdot c^2 = m_{ges} \cdot c^2)
ergibt sich daraus zwingend die Additivität der trägen Masse:
 \quad m_{ges} = \sum {m_i }) |
|
|
franz
Anmeldungsdatum: 04.04.2009
Beiträge: 11583
|
| franz Verfasst am: 19. Aug 2011 21:52 Titel: |
|
|
Man könnte auch, gaube ich, Bewegungsgleichungen aufstellen, die aus Vierervektoren und Konstanten bestehen und in der Form dem NEWTONschen Gesetz entsprechen. Bleibt "nur" die Frage nach der Struktur der Viererkraft.  |
|
|
|
Registrieren
Login
FAQ
Suchen
