| Autor |
Nachricht |
skywalker
Anmeldungsdatum: 01.04.2006
Beiträge: 198
|
 skywalker Verfasst am: 10. Nov 2007 13:39 Titel: Zustandsgleichungen finden |
 |
|
Hallo 
Also, ich komme mit der folgenden Aufgabe nicht so richtig klar:
Der Makrozustand eines System wird durch die Größen ) (Entropie und Volumen) definiert.
(a) Zeige, dass im Allgemeinen die innere Energie ) folgende funktionale Abhängigkeit erfüllt )
(b) Sei  , wobei ein Parameter ist. Finden sie die Zustandsgleicung in Formen ) und ) . Durch das Eliminieren von S in beiden Gleichungen finden sie ) im Gleichgewicht.
Zu der a) habe ich leider keine Idee, wie ich da anfangen soll.
zu der d), muss ich da "einfach" folgende Rechnung machen??:
 \Rightarrow dP = \left( \frac {\partial P}{\partial V}\right)_S dV + \left( \frac {\partial P}{\partial S}\right)_V dS )
bzw.
 \Rightarrow dT = \left( \frac {\partial T}{\partial V}\right)_S dV + \left( \frac {\partial T}{\partial S}\right)_V dS )
oder verstehe ich da was falsch?
Schonmal vielen dank, für eure Hilfe  |
|
 |
as_string
Moderator
Anmeldungsdatum: 09.12.2005
Beiträge: 5789
Wohnort: Heidelberg
|
| as_string Verfasst am: 10. Nov 2007 14:24 Titel: |
|
|
Hallo!
Ich bin da zwar auch immer ziemlich schlecht auf dem Gebiet, aber ich würde es so anfangen:
a) Die innere Energie ist ja:
 = TS - PV)
und das kannst Du da einfach in:
 = \left(T\frac{S}{V} - P\right)\cdot V = V\cdot f\left(\frac{S}{V}\right) \text{ mit } f\left(\frac{S}{V}\right) = T\cdot \left(\frac{S}{V}\right) - P)
umformen. Ich weißt nicht, ob das schon genügt für die a). Wichtig ist vielleicht noch, dass bei U die abhängigen Variablen ja S und V sind, so dass die Funktion f wirklich dann auch nur von S und V abhängt und p und T als konstant betrachtet werden kann, zumindest bei kleinen Änderungen von S und V. Aber das ist ziemlich schwammig, das wirst Du Dir noch genauer überlegen müssen, wie man da argumentieren muss...
Bei der b)
Da gilt doch, wenn ich mich recht erinnere:
_S = -S^\alpha (1-\alpha) V^{-\alpha} = (\alpha-1)\cdot \left(\frac{S}{V}\right)^\alpha)
und ähnlich dann für T. Das ist ja die Ableitung nach S bei konstantem V von U. Wenn man das hat, kann man ja die T(S, V) nach S auflösen und in die P(S, V) einsetzen.
Gruß
Marco
//Edit: Ich habe dann für T(S, V) das hier raus:
 = \alpha\cdot\left(\frac{S}{V}\right)^{\alpha-1})
Das kann man etwas umformen:
^{\alpha-1})
^{\alpha/(\alpha-1)} = \left(\frac{S}{V}\right)^{\alpha})
^{1-\frac{1}{\alpha}} = \left(\frac{S}{V}\right)^{\alpha})
Das kannst Du ja direkt in die P(S, V) einsetzen und hast dann (falls ich mich nicht verrechnet haben sollte...):
 = (\alpha-1)\cdot \left(\frac{\alpha}{T}\right)^{1-\frac{1}{\alpha}})
Zuletzt bearbeitet von as_string am 12. Nov 2007 16:44, insgesamt einmal bearbeitet |
|
|
schnudl
Moderator
Anmeldungsdatum: 15.11.2005
Beiträge: 6979
Wohnort: Wien
|
| schnudl Verfasst am: 10. Nov 2007 19:54 Titel: |
|
|
| as_string hat Folgendes geschrieben: |
|
Soll das nicht gezeigt werden? Du nimmst ja schon das Resultat vorweg - oder ? 
Da U eine extensive Variable ist und von den extensiven Variablen S und V abhängt, muss gelten
 = \lambda U(S,V))
Wenn ich hier nun nach 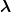 differenziere und anschliessend  setze, bekommt man:
)
Nun ist aber wegen des vollständigen Differenzials für reveresible Zustandsänderungen,
eben
und
und eingesetzt schliesslich
Danach kann ich mich der Argumentation von @as_string nur anschliessen.
_________________
Wenn du eine weise Antwort verlangst, musst du vernünftig fragen (Goethe) |
|
|
skywalker
Anmeldungsdatum: 01.04.2006
Beiträge: 198
|
| skywalker Verfasst am: 10. Nov 2007 22:24 Titel: |
|
|
schon mal vielen dank an euch beiden.
Ich versuche da gerade durchzusteigen. Ihr habt es ja auch sehr schön erklärt ... aber ich glaube ich scheitere anscheinend an den grundlagen.
ich verstehe nämlich nicht, woher man weiß, dass gilt:
 = \left(\frac{\partial U}{\partial V}\right)_S )
ich dachte nämlich, dass P(S,V) bedeuten würde, dass einmal nach S und V differenziert werden müsste ... aber dem scheint ja irgendwie nicht zu sein, oder?
Woher weiß ich also, was ich machen muss, wenn man sowas stehen hat wie halt zb P(S,V) oder T(S,V) ? |
|
|
schnudl
Moderator
Anmeldungsdatum: 15.11.2005
Beiträge: 6979
Wohnort: Wien
|
| schnudl Verfasst am: 10. Nov 2007 22:59 Titel: |
|
|
| skywalker hat Folgendes geschrieben: | ich glaube ich scheitere anscheinend an den grundlagen.
|
keine panik, wir blöffen auch nur...
Aber das ist immer noch besser als "Wetten das" anzuschauen...
| skywalker hat Folgendes geschrieben: |
 = - \left(\frac{\partial U}{\partial V}\right)_S )
|
Vorsicht, Minus !
Ich kann nur dazu Stellung nehmen, die anderen Aufgaben hab ich nicht angeschaut, das sie bei @as_string sicher in besten Händen sind.
Es gilt doch ein fundamentaler Zusammenhang, der meistens ganz am Anfang der Vorlesungen steht, nachdem die Entropie eingeführt worden ist. Es ist nichts anderes als die Energieerhaltung bei reversiblen Prozessen:
U ist eine Funktion von S und V, daher kann man auch das vollständige Differenzial bilden (reine Mathematik):
_V \, dS + \left( \frac{\partial U}{\partial V} \right)_S \, dV)
Wenn du nun die Koeffizienten (insbesondere von dV) vergleichst, kommst du auf die Behauptung. Ich hoffe es ist nun klar.
_________________
Wenn du eine weise Antwort verlangst, musst du vernünftig fragen (Goethe) |
|
|
skywalker
Anmeldungsdatum: 01.04.2006
Beiträge: 198
|
| skywalker Verfasst am: 11. Nov 2007 00:24 Titel: |
|
|
Achso, ok dann habe ich das jetzt verstanden
Danke. Dann kann ich schonmal vom verständnis her die b) abhacken.
Dann bräuchte ich aber noch klärungsbedarf zu der Teilaufgabe a).
Du sagtest
[quote="schnudl"] | as_string hat Folgendes geschrieben: |
Da U eine extensive Variable ist und von den extensiven Variablen S und V abhängt, muss gelten
|
ok, sowas hatten wir auch in der Vorlesung erwähnt.
Das bedeutet doch nichts anderes als zum beispiel die verdopplung (also  ) der inneren Energie woraus folgt, dass sich die Entropie und das Volumen auch verdoppeln muss. Ist das so richtig? Wenn ja, wieso benutzt man dann hier jetzt die extensive Variable? Es wäre doch einfach nur eine reelle Zahl, die jetzt mir doch bei diesem Problem nicht wirklich weiter helfen würde.
Kann man denn im prinzip als Antwort für diese Aufgabe auch nicht so vorgehen:
Es gilt bzw
mit dem vollständigen Differential würde dann folgen:
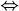
_V \, dS + \int \left( \frac{\partial U}{\partial V} \right)_S \, dV)
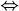
 = S \left( \frac{\partial U}{\partial S} \right)_V \, + V \left( \frac{\partial U}{\partial V} \right)_S \, )
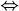
 = ST - pV = V f( S/V)) mit  = \frac{TV}{S}-p )
Im Prinzip wurde da doch nirgends die extensive Variable verwendet, oder? |
|
|
schnudl
Moderator
Anmeldungsdatum: 15.11.2005
Beiträge: 6979
Wohnort: Wien
|
| schnudl Verfasst am: 11. Nov 2007 13:41 Titel: |
|
|
| skywalker hat Folgendes geschrieben: |
Kann man denn im prinzip als Antwort für diese Aufgabe auch nicht so vorgehen:
_V }_{T}\, dS + \int \underbrace{ \left( \frac{\partial U}{\partial V} \right)_S }_{-p} \, dV)
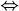
 = S \left( \frac{\partial U}{\partial S} \right)_V \, + V \left( \frac{\partial U}{\partial V} \right)_S \, )
|
Du gehst ja bei dieser Art von "Integration" davon aus, das sich p und T nicht ändern. Nur so kannst du es vor das Integralzeichen ziehen.
Nimm ein ideales Gas:
Wenn nun p=const:
oder
Wenn du also das Volumen änderst (dV - was du ja tust) , so ändert sich auch die Temperatur T . Und deshalb ist T während der Integration nicht konstant, was du aber angenommen hast. So kann man nicht integrieren, das Ergebnis stimmt nur zufällig, oder eben deshalb, weil U extensiv in V und S ist.
_________________
Wenn du eine weise Antwort verlangst, musst du vernünftig fragen (Goethe) |
|
|
skywalker
Anmeldungsdatum: 01.04.2006
Beiträge: 198
|
| skywalker Verfasst am: 11. Nov 2007 15:08 Titel: |
|
|
hmm,
heißt das also, dass diese Integration wie ich sie da jetzt aufgeschrieben hatte nur deswegen so durchgeführt werden kann, weil die größen T und p intensive Variablen sind. Was sie als Integrationskonstanten auszeichnet.
Die innere Energie ist hier nur von S und V abhängig.
prinzipiell ist mir das ganze jetzt klarer geworden. Aber muss trotzdem nochmal drüber nachdenken...
Nur mal angenommen, was ja wahrscheinlich nie eintretten kann, die Temperatur und der Druck wären auch extensive Variablen, dann müsste man nach p und T ebenfalls integrieren, oder? |
|
|
as_string
Moderator
Anmeldungsdatum: 09.12.2005
Beiträge: 5789
Wohnort: Heidelberg
|
| as_string Verfasst am: 12. Nov 2007 16:40 Titel: |
|
|
Hallo!
Das hat mit extensiv und intensiv nicht so direkt zu tun. Die innere Energie ist nunmal von den extensiven Variablen S, V und dann eigentlich noch von der Teilchenzahl N abhängig. Man kann jetzt nach und nach durch Legendre-Transformation die extensiven Variablen durch die zugehörigen intensiven ersetzen und erhält dann andere Potentiale (z. B. freie Energie F, Enthalpie H, Gibb's freie Enthalpie G, großkanonisches Potential), die dann teilweise von den intensiven Variablen abhängen. Z. B. die Freie Energie:
dF(T, V, N) = -S·dT-P·dV + µ·dN
Das kann man eben aus der inneren Energie durch Legendre-Transformation erhalten:
dE(S, V, N) = T·dS - P·dV + µ·dN
dF = d(E-TS) = dE - S·dT - T·dS = -S·dT-P·dV + µ·dN
Daraus kann man dann sehen, dass:
_{V, N})
_{T, N})
und entsprechend für die innere Energie:
_{V, N})
_{S, N})
Und so weiter für die anderen Potentiale (ich habe hier jetzt noch immer das chemische Potential µ und die Teilchenzahl mitgenommen. Wenn Ihr das noch nicht hattet, einfach den entsprechenden Summanden ignorieren).
Man nennt dann P und T, etc. "thermodynamische Kräft" der entsprechenden "thermodynamischen Potentiale", weil man sie ähnlich wie Kräfte aus einem Potential eines Kraftfeldes mit den Ableitungen raus bekommt.
Aber nochmal zu Deiner Aufgabe: Da war eben die innere Energie gegeben (ich habe hier jetzt E geschrieben, das ist aber das selbe, wie das, was Du mit U bezeichnet hast). Durch die Ableitungen bekommst Du dann direkt die entsprechenden thermodynamischen Kräfte zu dem Potential (ich hatte übrigens wirklich das Minus-Zeichen beim Druck vergessen... ich werd's gleich mal korrigieren). Aber so direkt hat das mit intensiv und extensiv nichts zu tun. Wenn man andere thermodynamische Potentiale hätte, dann würde man entsprechend die extensiven rausbekommen, wenn man die intensiven variiert. Bei der inneren Energie ist eben das besondere, dass sie nur von extensiven Größen (direkt) abhängt.
Gruß
Marco |
|
|
|
|
Registrieren
Login
FAQ
Suchen
