| Autor |
Nachricht |
razer
Anmeldungsdatum: 25.03.2005
Beiträge: 58
Wohnort: austria
|
 razer Verfasst am: 28. Okt 2007 12:47 Titel: Satz von Gauß, Fluss durch Kugeloberfläche razer Verfasst am: 28. Okt 2007 12:47 Titel: Satz von Gauß, Fluss durch Kugeloberfläche |
 |
|
Hallo!
Ich soll den Satz v Gauß verifizieren,indem ich von nem geg. Vektorfeld den Fluss durch die Oberfläche einer Kugel berechne.
Jetzt ist bei jeder Berechnung zwischen den zwei Ergebnissen der Fakor 1/3 verschieden,weil ich beim Volumenintegral ja r^2 nach dr integriere und beim Flächenintegral ja nicht,weshalb dieses im Ergebnis kein 1/3 drin hat.Beim Zylinder ist es der Faktor 1/2...
Weiß jemand schon meinen Fehler,ohne dass ich die ganze Rechnung hier poste?
LG
_________________
"Nur der Dumme braucht Ordnung, das Genie überblickt das Chaos!"
- Albert Einstein - |
|
 |
magneto42
Anmeldungsdatum: 24.06.2007
Beiträge: 854
|
 magneto42 Verfasst am: 28. Okt 2007 14:00 Titel: magneto42 Verfasst am: 28. Okt 2007 14:00 Titel: |
 |
|
Hallo razer.
Ich kann mir Ansatzweise vorstellen was Du meinst. Es hängt aber vom Ausdruck im Integranden ab, welche Faktoren beim Integrieren entstehen. Der Gauß'sche Satz gilt! Es muß also in der Rechnung auch so aufgehen. Du solltest also zumindest das Feld angeben um bessere Hilfestellung zu erhalten. |
|
 |
razer
Anmeldungsdatum: 25.03.2005
Beiträge: 58
Wohnort: austria
|
 razer Verfasst am: 28. Okt 2007 15:14 Titel: razer Verfasst am: 28. Okt 2007 15:14 Titel: |
 |
|
Ja,da hast du recht:
v = a(r.a) ...alles Vektoren
div(v) = |a|^2
hängt natürlich immer vom Integranden ab...in diesem Fall kommt aus df bzw dV für die Kugel ein r^2 hinzu,was bei dV zu integrieren ist und deswegen ein 1/3 liefert.
für df muss ich sowas machen denke ich:
v = |v| * e_r = |a|^2 * (r/|r|) * |r|
weil das df auch ein e_r hinten dran hat bleibt dann nurmehr
|a|^2*|r|
zu integrieren.
(dV= (r^2 sin(theta) dr dtheta dphi)e_r; df= (r^2 sin(theta) dtheta dphi)*e_r)
sry,dass ich den editor nicht verwendet habe,is beim nächsten post anders....
Grüße!
_________________
"Nur der Dumme braucht Ordnung, das Genie überblickt das Chaos!"
- Albert Einstein - |
|
 |
magneto42
Anmeldungsdatum: 24.06.2007
Beiträge: 854
|
 magneto42 Verfasst am: 28. Okt 2007 18:25 Titel: magneto42 Verfasst am: 28. Okt 2007 18:25 Titel: |
 |
|
Du hast natürlich Recht, daß der Faktor 1/3 bei der Integration über die Kugeloberfläche nicht auftaucht, aber den holt man bei der Integration über den Polarwinkel locker wieder herein  . .
Das Vektorfeld ist also )
Wenden wir und zuerst dem Volumenelement und Flächenelement zu:
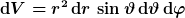
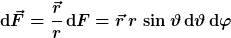
Soweit sind wir denke ich konform. Die Divergenz des Vektorfeldes ist auch korrekt und die Integration über das Kugelvolumen problemlos.
| razer hat Folgendes geschrieben: | | v = |v| * e_r = |a|^2 * (r/|r|) * |r| |
Dies stimmt nicht. Du sagst hier, daß das Vektorfeld immer in Richtung des Radiusvektors zeigt. Es ist aber so, daß das Feld immer in Richtung von 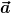 weist! weist!
Ich gebe Dir einen Hinweis was man machen kann. Man ist in der Wahl des Kugelkoordinatensystems frei. Also kann man die Polarachse in Richtung des Vektors 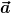 legen. Damit ergibt sich für das Skalarprodukt: legen. Damit ergibt sich für das Skalarprodukt:
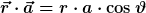
Versuche damit das Integral über die Kugeloberfläche aufzustellen und zu lösen. |
|
 |
razer
Anmeldungsdatum: 25.03.2005
Beiträge: 58
Wohnort: austria
|
 razer Verfasst am: 28. Okt 2007 18:55 Titel: razer Verfasst am: 28. Okt 2007 18:55 Titel: |
 |
|
Cool,danke 
Aber jetzt musst Du mir bitte nochmal erklären,was das bedeutet,das Feld zeigt immer in Richtung a,wie sehe ich das?
Und warum wurde aus dem S.-Produkt von r*a gleich |r|*|a|*cos(theta) ?
Hab hier noch zwei andere Probleme,wo das mit dem Faktor aus dem Integral gleich war,werd mich gleich mal versuchen 
_________________
"Nur der Dumme braucht Ordnung, das Genie überblickt das Chaos!"
- Albert Einstein - |
|
 |
magneto42
Anmeldungsdatum: 24.06.2007
Beiträge: 854
|
 magneto42 Verfasst am: 28. Okt 2007 19:14 Titel: magneto42 Verfasst am: 28. Okt 2007 19:14 Titel: |
 |
|
Hallo.
Der Term ) ist ein Skalarprodukt und hat als Ergebnis eine Zahl ohne Richtung. Also muß ist ein Skalarprodukt und hat als Ergebnis eine Zahl ohne Richtung. Also muß  sein. sein.
Das Skalarporukt ist definiert als
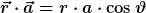
Wobei 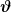 der Winkel zwischen den Vektoren ist. Wenn Du jetzt die Polarachse in Richtung von der Winkel zwischen den Vektoren ist. Wenn Du jetzt die Polarachse in Richtung von 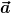 legst, ist dies auch gleichzeitig der Polarwinkel. legst, ist dies auch gleichzeitig der Polarwinkel.
Normalerweise nimmt man die Polarachse in Richtung der positiven z-Achse. Aber das muß aber nicht immer so sein. Da die Kugel symmetrisch in alle Raumrichtung ist, kann man das Koordinatensystem legen, wie es einem nützlich ist. Anders ist das bei Zylinderkoordinaten, wo die z-Achse eine ausgezeichnete Raumachse ist. |
|
 |
razer
Anmeldungsdatum: 25.03.2005
Beiträge: 58
Wohnort: austria
|
 razer Verfasst am: 28. Okt 2007 20:25 Titel: razer Verfasst am: 28. Okt 2007 20:25 Titel: |
 |
|
okay,also vielen Dank,hab ich gecheckt!
Neue Aufgabe:Feld bleibt das gleiche,nur diesmal keine Kugel,sondern ein Zyliner(Länge l,Radius r).a steht senkrecht auf die Zylinderachse =>a || r !?
Kann ich
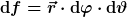
machen?Wenn ja,dann kann ich das Skalarprodukt als r*a*cosphi schreiben und integrier dann über cos^2 von 0 - 2*pi und bekomm da meinen faktor zwei wieder...
gruß,
r.
_________________
"Nur der Dumme braucht Ordnung, das Genie überblickt das Chaos!"
- Albert Einstein - |
|
 |
magneto42
Anmeldungsdatum: 24.06.2007
Beiträge: 854
|
 magneto42 Verfasst am: 28. Okt 2007 21:23 Titel: magneto42 Verfasst am: 28. Okt 2007 21:23 Titel: |
 |
|
Für das Flächenelement des Zylinders muß man Grundsätzlich eine Fallunterscheidung gemacht werden bezüglich des Mantels und der Deckflächen. Für die Deckflächen gilt:
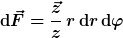
Da hier 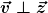 verschwindet das Intergral. verschwindet das Intergral.
Für den Mantel gilt:
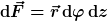
Man kann die polare Achse wieder in Richtung von 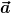 wählen und erhält das Skalarprodukt, wie Du es angegeben hast: wählen und erhält das Skalarprodukt, wie Du es angegeben hast:
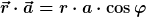
Der Rest der Vorgehensweise ist analog, wie vorher. |
|
 |
razer
Anmeldungsdatum: 25.03.2005
Beiträge: 58
Wohnort: austria
|
 razer Verfasst am: 28. Okt 2007 21:31 Titel: razer Verfasst am: 28. Okt 2007 21:31 Titel: |
 |
|
Okay,das war sehr einleuchtend,vielen Dank!
Ich habe noch bei nem ähnlichen Bsp ein Problem-werd dafür aber nen neuen Thread aufmachen.
Danke für deine Hilfe,
r.
_________________
"Nur der Dumme braucht Ordnung, das Genie überblickt das Chaos!"
- Albert Einstein - |
|
 |
|
















 .
.
