| Autor |
Nachricht |
Kelvin1995
Anmeldungsdatum: 09.01.2022
Beiträge: 64
|
 Kelvin1995 Verfasst am: 06. Jun 2022 14:53 Titel: Postulate der Mechanik Kelvin1995 Verfasst am: 06. Jun 2022 14:53 Titel: Postulate der Mechanik |
 |
|
Hallo kann man die Postulate der speziellen Relativitätstheorie so formulieren?
1. Die geometrische Bühne ist der vierdimensionale Minkowski-Raum. Es gibt eine Äquivalenzklasse an Bezugssystemen bzgl denen das Abstandsquadrat  invariant ist. Diese Bezugssysteme heißen Inertialsysteme invariant ist. Diese Bezugssysteme heißen Inertialsysteme
2. In jedem Inertialsystem gelten dieselben physikalischen Gesetze
3. Die Gesamtheit aller Orte und Geschwindigkeiten eines Systems zu einem bestimmten Zeitpunkt heißt Zustand. Kennt man den Zustand eines abgeschlossenen Systems zu einem bestimmten Zeitpunkt, kennt man den Zustand zu jedem beliebigen anderen Zeitpunkt.
Daraus ließe sich alles herleiten. Insbesondere käme man auf Lorentz-boosts als Umrechnung zwischen den Inertialsystemen.
Für die Newtonsche Mechanik müsste man jetzt nur das Invariante Abstandsquadrat zu  ändern ändern
Das ist dann der wesentliche Unterschied zwischen newtonscher Mechanik und SRT.
Wie müsste man die Postulate ändern/erweitern um zur allgemeinen Relativitätstheorie zu kommen?
Gibt es dann überhaupt noch Inertialsystemen oder müsste man den Begriff des lokalen Inertialsystems einführen?
Oder reicht es aus Minkowski Raum durch semi-riemannsche Mannigfaltigkeit zu ersetzen?
Vielen Dank |
|
 |
Aruna
Anmeldungsdatum: 28.07.2021
Beiträge: 795
|
 Aruna Verfasst am: 06. Jun 2022 15:10 Titel: Re: Postulate der Mechanik Aruna Verfasst am: 06. Jun 2022 15:10 Titel: Re: Postulate der Mechanik |
 |
|
| Kelvin1995 hat Folgendes geschrieben: |
Oder reicht es aus Minkowski Raum durch semi-riemannsche Mannigfaltigkeit zu ersetzen?
|
Kann man daraus das Äquivalenzprinzip ableiten? |
|
 |
Kelvin1995
Anmeldungsdatum: 09.01.2022
Beiträge: 64
|
 Kelvin1995 Verfasst am: 06. Jun 2022 15:26 Titel: Re: Postulate der Mechanik Kelvin1995 Verfasst am: 06. Jun 2022 15:26 Titel: Re: Postulate der Mechanik |
 |
|
| Aruna hat Folgendes geschrieben: | | Kelvin1995 hat Folgendes geschrieben: |
Oder reicht es aus Minkowski Raum durch semi-riemannsche Mannigfaltigkeit zu ersetzen?
|
Kann man daraus das Äquivalenzprinzip ableiten? |
Meinst du dass schwere Masse und träge Masse äquivalent sind oder dass in jedem lokalen Inertialsystem die Gesetze der SRT gelten? |
|
 |
Aruna
Anmeldungsdatum: 28.07.2021
Beiträge: 795
|
 Aruna Verfasst am: 06. Jun 2022 15:39 Titel: Re: Postulate der Mechanik Aruna Verfasst am: 06. Jun 2022 15:39 Titel: Re: Postulate der Mechanik |
 |
|
| Kelvin1995 hat Folgendes geschrieben: | | Aruna hat Folgendes geschrieben: | | Kelvin1995 hat Folgendes geschrieben: |
Oder reicht es aus Minkowski Raum durch semi-riemannsche Mannigfaltigkeit zu ersetzen?
|
Kann man daraus das Äquivalenzprinzip ableiten? |
Meinst du dass schwere Masse und träge Masse äquivalent sind oder dass in jedem lokalen Inertialsystem die Gesetze der SRT gelten? |
Mir scheint, Letzteres reicht, dann folgt Ersteres. |
|
 |
Kelvin1995
Anmeldungsdatum: 09.01.2022
Beiträge: 64
|
 Kelvin1995 Verfasst am: 06. Jun 2022 15:54 Titel: Kelvin1995 Verfasst am: 06. Jun 2022 15:54 Titel: |
 |
|
Ich glaube eher nicht.
Ich möchte als erstes mir darüber Gedanken machen wie man den Begriff des lokalen Inertialsystems mathematisch präzisiert.
Meine Vorstellungen dazu:
Gegeben sei eine vierdimensionale Semi-Riemannsche Mannigfaltigkeit ) mit mit 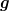 als den zweifach kovarianten Fundamentaltensor. als den zweifach kovarianten Fundamentaltensor.
Dann existiert zu einer Umgebung eines Punkt p eine Karte ) . Diese Karte induziert eine Basis des Tangentialraums . Diese Karte induziert eine Basis des Tangentialraums

Aus den Werten von g mit diesen Basisvektoren ist g vollständig gegeben
Ein lokales Inertialsystem ist jetzt eine Karte, so dass das in den R^4 übertragene Pseudo-Skalarprodukt dem Minkowski-Skalarprodukt entspricht. In diesem Raum nehmen die physikalischen Gesetze die Form der Gesetze der SRT an.
Kann man das so sagen? |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 06. Jun 2022 16:54 Titel: index_razor Verfasst am: 06. Jun 2022 16:54 Titel: |
 |
|
Ein lokales Inertialsystem ist z.B. durch folgende Eigenschaften charakterisiert. Die Basisvektoren müssen in einem Punkt P orthonormal sein, also  = \pm \delta_{ik}) (Vorzeichen entsprechend der Signatur von g) und die Zusammenhangskoeffizienten müssen in P verschwinden (Vorzeichen entsprechend der Signatur von g) und die Zusammenhangskoeffizienten müssen in P verschwinden \partial_j = 0) . Wegen der zweiten Forderung folgen unbeschleunigte Teilchen der Bahnkurve . Wegen der zweiten Forderung folgen unbeschleunigte Teilchen der Bahnkurve

was Ausdruck des Trägheitsprinzips im lokalen Inertialsystem ist. Wegen der Krümmung der Raumzeit können beide Bedingungen im allgemeinen nur in einem Ereignis erfüllt sein. (Aus deiner Formulierung geht das nicht klar hervor.)
_________________
It is just this lack of connection to a concern with truth -- this indifference to how things really are -- that I regard as of the essence of bullshit. -- Harry G. Frankfurt |
|
 |
Kelvin1995
Anmeldungsdatum: 09.01.2022
Beiträge: 64
|
 Kelvin1995 Verfasst am: 06. Jun 2022 18:01 Titel: Kelvin1995 Verfasst am: 06. Jun 2022 18:01 Titel: |
 |
|
Trägt die Bedingung, dass die Zusammenhangskoeffizienten null sein sollen, dem Rechnung, dass die SRT Gesetze auch noch in der unmittelbaren Umgebung des Punktes p gelten sollen?
Zusammenhänge sollen doch eine Verallgemeinerung von Richtungsableitungen für Mannigfaltigkeiten sein, d.h. man geht in Richtung  und schaut wie sich und schaut wie sich  verändert verändert
oder anders ausgedrückt, man stellt einen Zusammenhang zwischen dem Tangentialraum p und den unmittelbar umliegenden Tangentialräumen her und wenn man in diese Tangentialräume übergeht, soll sich an den Basisvektoren und deren Beziehungen untereinander nichts geändert haben.
oder wie habe ich mir das vorzustellen?
Würdest du denn als lokales Inertialsystem eine entsprechende Karte oder den Raum in den diese Karte abbildet, bezeichnen? |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 06. Jun 2022 20:03 Titel: index_razor Verfasst am: 06. Jun 2022 20:03 Titel: |
 |
|
| Kelvin1995 hat Folgendes geschrieben: | | Trägt die Bedingung, dass die Zusammenhangskoeffizienten null sein sollen, dem Rechnung, dass die SRT Gesetze auch noch in der unmittelbaren Umgebung des Punktes p gelten sollen? |
Nein, eigentlich nicht. Die Zusammenhangskoeffizienten haben nichts mit Abweichungen von den SRT-Gesetzen oder ähnlichem zu tun. Sie beschreiben eher die Eigenbeschleunigung des Koordinatensystems, d.h. die seines Ursprungs sowie die Drehung der Achsen. Diese verschwinden bei globalen Inertialsystemen einfach per Definition. Lokale Inertialsysteme stellen lediglich die bestmögliche Näherung an ein globales Inertialsystem mit Ursprung P dar, die die Krümmung noch erlaubt.
Die Abweichung vom globalen Inertialsystem kann man mittels der Abweichung der Metrikkoeffizienten von der Lorentzschen Form  parameterisieren, z.B. parameterisieren, z.B.
 = \eta_{ik} + g_{ik, n}(P)x^n + \frac{1}{2}g_{ik, nm}(P)x^n x^m + ...)
Der Term erster Ordnung ) ist eindeutig durch die Zusammenhangskoeffizienten im Punkt P bestimmt und läßt sich immer wegtransformieren. Bei der zweiten Ordnung geht das aber nicht mehr, da sie von der Krümmung abhängt. Alle diese Terme können nur verschwinden wenn die Raumzeit flach ist. Das beste, was man erreichen kann, ist also ist eindeutig durch die Zusammenhangskoeffizienten im Punkt P bestimmt und läßt sich immer wegtransformieren. Bei der zweiten Ordnung geht das aber nicht mehr, da sie von der Krümmung abhängt. Alle diese Terme können nur verschwinden wenn die Raumzeit flach ist. Das beste, was man erreichen kann, ist also
1)  = \eta_{ik}) und und
2)  = 0.)
Und das nennt man dann einfach "lokales Inertialsystem".
| Zitat: |
Zusammenhänge sollen doch eine Verallgemeinerung von Richtungsableitungen für Mannigfaltigkeiten sein, d.h. man geht in Richtung  und schaut wie sich und schaut wie sich  verändert verändert
oder anders ausgedrückt, man stellt einen Zusammenhang zwischen dem Tangentialraum p und den unmittelbar umliegenden Tangentialräumen her und wenn man in diese Tangentialräume übergeht, soll sich an den Basisvektoren und deren Beziehungen untereinander nichts geändert haben.
oder wie habe ich mir das vorzustellen?
|
Wenn du nach der physikalischen Anschauung hinter dieser Bedingung fragst, würde ich sagen, sie beschreibt, daß ein lokales Inertialsystem ein drehungsfreies, starres Ruhesystem eines frei fallenden Beobachters ist.
| Zitat: |
Würdest du denn als lokales Inertialsystem eine entsprechende Karte oder den Raum in den diese Karte abbildet, bezeichnen? |
Auf jeden Fall die Karte. Die Bildmenge ist einfach eine Teilmenge von 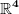 ohne bestimmte Eigenschaften. ohne bestimmte Eigenschaften.
_________________
It is just this lack of connection to a concern with truth -- this indifference to how things really are -- that I regard as of the essence of bullshit. -- Harry G. Frankfurt |
|
 |
Kelvin1995
Anmeldungsdatum: 09.01.2022
Beiträge: 64
|
 Kelvin1995 Verfasst am: 07. Jun 2022 20:55 Titel: Kelvin1995 Verfasst am: 07. Jun 2022 20:55 Titel: |
 |
|
Ok danke dafür.
Dann weiter im Text.
Formulieren wir mal die folgenden Postulate:
1. In einem lokalen Inertialsystem gelten die Gesetze der SRT
2. Die Gesetze der ART nehmen in jedem Bezugssystem dieselbe Form an
Sind dann Bezugssysteme einfach beliebige Karten?
"lokales Inertialsystem" ist so definiert wie du es gemacht hast (verschwinden der Zusammenhangskomponenten und orthonormale Basisvektoren).
Dann reicht das doch aus um die Geodätengleichung herzuleiten oder?
D.h. man nimmt ein lokales Inertialsystem, nimmt die Bewegungsgleichung der SRT und macht dann einen Kartenwechsel in ein anderes System und das Gesetz der SRT muss jetzt so erweitert werden, dass es unter so einer Transformation forminvariant ist. Kann man das so sagen? Ist das für die Geodätengleichung ausreichend? |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 08. Jun 2022 14:33 Titel: index_razor Verfasst am: 08. Jun 2022 14:33 Titel: |
 |
|
Vielleicht zunächst mal ein etwas allgemeiner Kommentar. Wenn du Postulate der ART formulieren willst, warum forderst du dann nicht einfach, daß i) die Raumzeit eine pseudo-riemannsche Mannigfaltigkeit ist und ii) die Einstein-Gleichungen gelten? Daraus kannst du die "Geodätenhypothese" unter den richtigen Anfangsbedingungen an den Energie-Impuls-Tensor T herleiten, falls das dein Ziel ist. Die Definition von lokalen Inertialsystemen (sowie der Beweis, daß sie immer existieren) erfordert ohnehin i).
Natürlich wäre es auch schön ein Prinzip zu haben, aus dem man die Gleichungen der Felder ableiten kann, die in T vorkommen. Das ist vermutlich deine Intention hinter diesen Postulaten:
| Kelvin1995 hat Folgendes geschrieben: |
1. In einem lokalen Inertialsystem gelten die Gesetze der SRT
2. Die Gesetze der ART nehmen in jedem Bezugssystem dieselbe Form an
|
Aber solche Forderungen sind im allgemeinen wohl weniger nützlich als man hoffen könnte. Zum Beispiel könnte man aus beiden die Regel  herauslesen, um von der "Form" der Feldgleichung in einem globalen Inertialsystem der SRT auf die "Form" der entsprechenden Gleichung im beliebigen Koordinatensystem der ART zu schließen. Aber die SRT-Gleichungen haben verschiedene äquivalente Formen. Und es macht einen Unterschied ob man z.B. die obige Regel auf die Maxwellgleichung in der Form herauslesen, um von der "Form" der Feldgleichung in einem globalen Inertialsystem der SRT auf die "Form" der entsprechenden Gleichung im beliebigen Koordinatensystem der ART zu schließen. Aber die SRT-Gleichungen haben verschiedene äquivalente Formen. Und es macht einen Unterschied ob man z.B. die obige Regel auf die Maxwellgleichung in der Form  = j^\nu) anwendet oder auf die äquivalente Gleichung anwendet oder auf die äquivalente Gleichung  = j^\nu) . Die Vertauschung der partiellen Ableitungen hat keine Konsequenz, aber Vertauschung der kovarianten Ableitungen führt einen Krümmungsterm ein. Die korrekte Gleichung (mit Ladungserhaltung) ergibt sich nur aus . Die Vertauschung der partiellen Ableitungen hat keine Konsequenz, aber Vertauschung der kovarianten Ableitungen führt einen Krümmungsterm ein. Die korrekte Gleichung (mit Ladungserhaltung) ergibt sich nur aus  . .
| Zitat: |
Sind dann Bezugssysteme einfach beliebige Karten?
|
Bezugssysteme sind Karten, die sich näherungsweise durch ideale Uhren und Maßstäbe realisieren lassen. Ich würde also erwarten, daß sie genau einen zeitartigen und drei raumartige Basisvektoren haben.
_________________
It is just this lack of connection to a concern with truth -- this indifference to how things really are -- that I regard as of the essence of bullshit. -- Harry G. Frankfurt |
|
 |
Kelvin1995
Anmeldungsdatum: 09.01.2022
Beiträge: 64
|
 Kelvin1995 Verfasst am: 04. Jul 2022 22:59 Titel: Kelvin1995 Verfasst am: 04. Jul 2022 22:59 Titel: |
 |
|
| index_razor hat Folgendes geschrieben: | Daraus kannst du die "Geodätenhypothese" unter den richtigen Anfangsbedingungen an den Energie-Impuls-Tensor T herleiten, falls das dein Ziel ist.
|
Magst du das vielleicht erläutern? Also der Ansatz reicht mir. Ich komme nicht drauf wie man die Geodätengleichung aus den Einsteinschen Feldgleichungen und der Annahme, dass die Raumzeit eine pseudo-riemannsche Mannigfaltigkeit ist, herleiten kann. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 06. Jul 2022 08:46 Titel: index_razor Verfasst am: 06. Jul 2022 08:46 Titel: |
 |
|
| Kelvin1995 hat Folgendes geschrieben: | | index_razor hat Folgendes geschrieben: | Daraus kannst du die "Geodätenhypothese" unter den richtigen Anfangsbedingungen an den Energie-Impuls-Tensor T herleiten, falls das dein Ziel ist.
|
Magst du das vielleicht erläutern? Also der Ansatz reicht mir. Ich komme nicht drauf wie man die Geodätengleichung aus den Einsteinschen Feldgleichungen und der Annahme, dass die Raumzeit eine pseudo-riemannsche Mannigfaltigkeit ist, herleiten kann. |
Das Argument ist etwa analog zur Herleitung der Lorentzkraft aus den Maxwellgleichungen und der Impulserhaltung.
Aus den Einsteingleichungen folgt die kovariante Energie-Impulserhaltung  . Der Energie-Impuls-Tensor . Der Energie-Impuls-Tensor 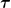 eines Testteilchens soll einen vernachlässigbaren Beitrag zur Gravitation leisten. Aus dieser Annahme folgt die Bewegungsgleichung eines Testteilchens soll einen vernachlässigbaren Beitrag zur Gravitation leisten. Aus dieser Annahme folgt die Bewegungsgleichung  , wobei die Metrik, die den Zusammenhang , wobei die Metrik, die den Zusammenhang  definiert durch definiert durch 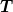 allein bestimmt ist. Die räumliche Ausdehnung von allein bestimmt ist. Die räumliche Ausdehnung von 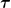 muß klein genug sein, damit man die Änderung der Zusammenhangskoeffizienten in der Umgebung des Testteilchens ab der zweiten Ordnung vernachlässigen kann. muß klein genug sein, damit man die Änderung der Zusammenhangskoeffizienten in der Umgebung des Testteilchens ab der zweiten Ordnung vernachlässigen kann.
Die Idee ist dann, zu zeigen, daß der Energieschwerpunkt von 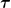
 = \frac{1}{M^{00}} \int_{t=\rm{const.}}\dd^3 x\,\sqrt{g}x^\mu\tau^{00}\qquad \left[\stackrel{!}{=}\frac{1}{M^{\nu\lambda}} \int_{t=\rm{const.}}\dd^3 x\,\sqrt{g}x^\mu\tau^{\nu\lambda}\right])
der Geodätengleichung genügt. Im Prinzip könnten für die Schwerpunkte verschiedener Komponenten von 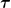 verschiedene Bewegungsgleichungen gelten. Aber man kann es als Teil der Definition eines "strukturlosen" Testteilchens ansehen, daß alle diese Schwerpunkte zusammenfallen. verschiedene Bewegungsgleichungen gelten. Aber man kann es als Teil der Definition eines "strukturlosen" Testteilchens ansehen, daß alle diese Schwerpunkte zusammenfallen.
_________________
It is just this lack of connection to a concern with truth -- this indifference to how things really are -- that I regard as of the essence of bullshit. -- Harry G. Frankfurt |
|
 |
|















