| Autor |
Nachricht |
Kelvin1995
Anmeldungsdatum: 09.01.2022
Beiträge: 64
|
 Kelvin1995 Verfasst am: 28. Mai 2022 15:03 Titel: Freiheitsgrade von Photonen Kelvin1995 Verfasst am: 28. Mai 2022 15:03 Titel: Freiheitsgrade von Photonen |
 |
|
Warum haben Photonen nur zwei Polarisationsfreiheitsgrade obwohl es sich um Spin-1-Teilchen handelt? Dann müsste es doch -1, 0, und 1 Photonen geben?
Was passiert mit den longitudinalen Photonen?
Ich bin mir ziemlich sicher, dass es was mit der Masselosigkeit der Photonen zu tun hat, verstehe aber nicht wieso die Masselosigkeit dazu führt, dass ein Freiheitsgrad verschwindet. |
|
 |
Aruna
Anmeldungsdatum: 28.07.2021
Beiträge: 795
|
 Aruna Verfasst am: 28. Mai 2022 15:18 Titel: Re: Freiheitsgrade von Photonen Aruna Verfasst am: 28. Mai 2022 15:18 Titel: Re: Freiheitsgrade von Photonen |
 |
|
| Kelvin1995 hat Folgendes geschrieben: | Warum haben Photonen nur zwei Polarisationsfreiheitsgrade obwohl es sich um Spin-1-Teilchen handelt? Dann müsste es doch -1, 0, und 1 Photonen geben?
Was passiert mit den longitudinalen Photonen?
|
was sind denn longitudinale Photonen?
Wikipedia meint [Hervorhebungen durch mich]:
| Zitat: | Zirkular polarisierte E-M-Wellen mit Energie 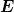 und Kreisfrequenz und Kreisfrequenz 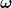 haben nach den Maxwell-Gleichungen einen Drehimpuls der Größe haben nach den Maxwell-Gleichungen einen Drehimpuls der Größe  , pro Photon mit , pro Photon mit  also genau den Drehimpulsbetrag von also genau den Drehimpulsbetrag von 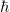 . Photonen sind also Spin-1-Teilchen und somit Bosonen. Es können also beliebig viele Photonen denselben quantenmechanischen Zustand besetzen, was zum Beispiel in einem Laser realisiert wird. . Photonen sind also Spin-1-Teilchen und somit Bosonen. Es können also beliebig viele Photonen denselben quantenmechanischen Zustand besetzen, was zum Beispiel in einem Laser realisiert wird.
Während etwa der Elektronenspin parallel oder antiparallel zu einer beliebig vorgegebenen Richtung ist,[14] kann der Photonenspin wegen fehlender Masse nur parallel oder antiparallel zur Flugrichtung, also zu seinem Impuls, orientiert sein. Die Helizität der Photonen einer zirkular polarisierten Welle ist daher eine charakteristische Größe. Wird durch einen Spiegel die Ausbreitungsrichtung umgekehrt, oder wird die Rotationsrichtung umgekehrt, zum Beispiel durch eine λ/2-Platte, so wechselt die Helizität das Vorzeichen.
Linear polarisierte elektromagnetische Wellen bestehen aus der Überlagerung von rechts und links polarisierten Photonen. Auch ein einzelnes Photon kann linear polarisiert werden, indem zwei entgegengesetzt zirkular polarisierte Zustände überlagert werden. Der Erwartungswert des Drehimpulses längs der Flugrichtung ist dann Null, jedoch ist in einem linear polarisierten Photon mit je 50 % Wahrscheinlichkeit ein links oder ein rechts zirkular polarisiertes Photon zu finden.
https://de.wikipedia.org/wiki/Photon#Spin
|
|
|
 |
Kelvin1995
Anmeldungsdatum: 09.01.2022
Beiträge: 64
|
 Kelvin1995 Verfasst am: 28. Mai 2022 15:48 Titel: Re: Freiheitsgrade von Photonen Kelvin1995 Verfasst am: 28. Mai 2022 15:48 Titel: Re: Freiheitsgrade von Photonen |
 |
|
| Aruna hat Folgendes geschrieben: |
was sind denn longitudinale Photonen?
|
"longitudinale Photonen" wären Photonen bei dem die z-Komponente (wenn man jetzt von der z-Darstellung ausgeht) des Photonenspins den Wert 0 hätte, die man aber nicht beobachtet, was aber ein möglicher Wert ist, wenn man von er reinen Drehimpulsalgebra ausgeht.
Ich weiß nicht ob der wikipedia-Auszug meine Frage beantwortet.
Zumindest über den Teil mit der Helizität habe ich mir schonmal Gedanken gemacht.
Bei einem massebehaftetem Teilchen hängt die Helizität vom Bezugssystem ab. Ich könnte mich ja in ein Inertialsystem transformieren von dem ausgesehen sich der Impuls des Teilchens in umgekehrter Richtung zeigt.
Bei einem messelosem Teilchen, welches sich dann mit Lichtgeschwindigkeit bewegt, gibt es so ein Inertialsystem nicht. Da ist die Helizität tatsächlich ein innerer Freiheitsgrad, der den Zustand des Teilchens charakterisiert. Ist der dritte Freiheitsgrad also gar nicht weg, sondern steckt in der Helizität? |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 28. Mai 2022 16:35 Titel: Re: Freiheitsgrade von Photonen index_razor Verfasst am: 28. Mai 2022 16:35 Titel: Re: Freiheitsgrade von Photonen |
 |
|
| Kelvin1995 hat Folgendes geschrieben: | | Ich bin mir ziemlich sicher, dass es was mit der Masselosigkeit der Photonen zu tun hat, verstehe aber nicht wieso die Masselosigkeit dazu führt, dass ein Freiheitsgrad verschwindet. |
Der Freiheitsgrad verschwindet nicht. Er ist von vornherein nie da. Die einzigen Freiheitsgrade, die freie masselose Teilchen charakterisieren sind Impuls und Helizität. Wie du selbst geschrieben hast, ist die Helizität sogar eine Invariante unter eigentlichen Lorentztransformationen. Raumspiegelungen P hingegen bilden Zustände mit Helizität 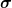 auf Zustände mit Helizität auf Zustände mit Helizität  ab. Damit gibt es zwei Möglichkeiten: 1) die Theorie ist nicht invariant unter P. Dann klassifiziert man Teilchensorten nach Invarianten unter der eigentlichen Lorentzgruppe und Teilchen mit Helizität +1 und -1 gehören zu verschiedenen Sorten. 2) Die Theorie ist invariant unter P. Das trifft auf die QED zu. Dann klassifiziert man Teilchen nach Invarianten unter der vollen Lorentzgruppe, z.B. ab. Damit gibt es zwei Möglichkeiten: 1) die Theorie ist nicht invariant unter P. Dann klassifiziert man Teilchensorten nach Invarianten unter der eigentlichen Lorentzgruppe und Teilchen mit Helizität +1 und -1 gehören zu verschiedenen Sorten. 2) Die Theorie ist invariant unter P. Das trifft auf die QED zu. Dann klassifiziert man Teilchen nach Invarianten unter der vollen Lorentzgruppe, z.B.  . Alle Zustände mit . Alle Zustände mit  (und identischen weiteren inneren Quantenzahlen, falls vorhanden), gehören dann zur selben Sorte. (und identischen weiteren inneren Quantenzahlen, falls vorhanden), gehören dann zur selben Sorte.
Die beiden Polaristationsrichtungen begegnen einem wieder, wenn man versucht aus den Erzeugern und Vernichtern dieser Teilchen freie Feldoperatoren zu konstruieren. Diese müssen dann die Coulombeichbedingung  erfüllen, d.h. erfüllen, d.h. =0) , was nochmal ausdrückt, daß es keine longitudinal polarisierten freien masselosen Felder gibt. Aber das ist natürlich per Konstruktion der Fall und es ist, wie gesagt, nichts verschwunden, was vorher da war. , was nochmal ausdrückt, daß es keine longitudinal polarisierten freien masselosen Felder gibt. Aber das ist natürlich per Konstruktion der Fall und es ist, wie gesagt, nichts verschwunden, was vorher da war.
_________________
It is just this lack of connection to a concern with truth -- this indifference to how things really are -- that I regard as of the essence of bullshit. -- Harry G. Frankfurt
Zuletzt bearbeitet von index_razor am 28. Mai 2022 16:41, insgesamt einmal bearbeitet |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18072
|
 TomS Verfasst am: 28. Mai 2022 16:39 Titel: Re: Freiheitsgrade von Photonen TomS Verfasst am: 28. Mai 2022 16:39 Titel: Re: Freiheitsgrade von Photonen |
 |
|
index_razor war schnell:-)
| Kelvin1995 hat Folgendes geschrieben: | Warum haben Photonen nur zwei Polarisationsfreiheitsgrade obwohl es sich um Spin-1-Teilchen handelt? Dann müsste es doch -1, 0, und 1 Photonen geben?
Was passiert mit den longitudinalen Photonen?
Ich bin mir ziemlich sicher, dass es was mit der Masselosigkeit der Photonen zu tun hat, verstehe aber nicht wieso die Masselosigkeit dazu führt, dass ein Freiheitsgrad verschwindet. |
Dazu kenne ich zwei Erklärung:
Nach der Wigner-Klassifizierung transformieren physikalische Zustände gemäß irreduzibler Darstellungen der PoincareGruppe. Im Falle masseloser Teilchen führt dies nicht auf Spin- sondern auf die Helizität, die irreduzible Darstellung ist daher zwei- und nicht dreidimensional.
Zunächst hat das Photon als Vierervektor vier Komponenten. Eine Komponente – am einfachsten in der temporalen Eichung  verschwindet mittels einer Eichtransformation. Darüber hinaus existiert noch eine Rest-Eichsymmetrie, die die temporale Eichung respektiert; mittels dieser kann eine weitere Komponente eliminiert werden. Alternativ erkennt man dass mittels der Lösung des gauß’schen Gesetzes im Vakuum: verschwindet mittels einer Eichtransformation. Darüber hinaus existiert noch eine Rest-Eichsymmetrie, die die temporale Eichung respektiert; mittels dieser kann eine weitere Komponente eliminiert werden. Alternativ erkennt man dass mittels der Lösung des gauß’schen Gesetzes im Vakuum:

Mittels Fouriertransformation folgt

D.h. der elektrische Feldstärkenvektor steht im Impulsraum senkrecht auf dem Wellenzahlvektor k, d.h. im Ortsraum senkrecht zur Ausbreitungsrichtung; das Gaußgesetz eliminiert demnach die longitudinale Polarisation.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8582
|
 jh8979 Verfasst am: 28. Mai 2022 17:23 Titel: Re: Freiheitsgrade von Photonen jh8979 Verfasst am: 28. Mai 2022 17:23 Titel: Re: Freiheitsgrade von Photonen |
 |
|
| TomS hat Folgendes geschrieben: |
Nach der Wigner-Klassifizierung transformieren physikalische Zustände gemäß irreduzibler Darstellungen der PoincareGruppe. Im Falle masseloser Teilchen führt dies nicht auf Spin- sondern auf die Helizität, die irreduzible Darstellung ist daher zwei- und nicht dreidimensional.
|
Tatsächlich ist die Wigner Little Group für masselose Teiclhen E(2): Zwei Translationen und eine Rotation in der zweidimensionalen Ebene, also insgesamt dreidimensional. Die beiden Translationsfreiheitsgrade hängen aber mit der Eichhfreiheit zuammen, so dass die Rotatiom als physikalische Dimesion übrig bleibt. Das nennen wir Helizität.
(Daher halte ich den Unterschied zwischen Helizität (E(2)) und Spin (SO(3)) bei masselosen und massiven Teilchen auch für wichtig  ) ) |
|
 |
|
|
















 )
)