| Autor |
Nachricht |
vtxt1103
Anmeldungsdatum: 14.11.2021
Beiträge: 302
|
 vtxt1103 Verfasst am: 16. Jan 2022 14:34 Titel: Schneepflug Theoretische Physik |
 |
|
Meine Frage:
Hallo liebe Leute,
ich habe hier eine Aufgabe, die mich an den Rand der verzweiflung bring, da ich überhaupt gar keinen Anhaltpunkt habe wie diese zu lösen bzw zu rechen ist, es geht um Folgendes:
Eine Bergstraße ist mit einer Schneeschicht der Höhe h = h0 = const. bedeckt.
Ein Schneepflug der Breite b fährt diese Straße hinunter, was durch die Trajektorie  beschrieben wird.
Wobei H die Höhe des Berges 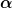und  und  Positive Konstanten sind. Für gilt außerdem 
Das Fahrzeug fährt zum Zeitpunkt t = 0 los. Zu welchem Zeitpunkt T kommt es am Fuße des Berges an
(dieser befindet sich bei z = 0)?
Wie viel Schnee hat die Maschine zu diesem
Zeitpunkt bereits geräumt? Wie verändert sich diese Menge wenn die Höhe der
Schneeschicht von z abhängt,? = \frac{h_0} {H}z )
Hinweis: Nimm an, dass die Maschine nicht breiter als die Straße ist und
der Schnee die Maschine nicht überragt. Es gilt:
\dd x = \frac {2}{15B^2}(A + Bx)^\frac{3}{2}*(5BC+2AD-3BDx)) + const., mit A, B, C, D konstant und
positiv.
Ich bedanke mich jetzt schonmal für eure Hilfe
Meine Ideen:
Wie gesagt mich verwirrt die Aufgabe Extrem und ich habe absolut gar keinen Anhaltspunkt wie ich was machen soll
Würde mich freuen wenn mich jemand bei der Bearbeitung unterstützen würde
|
|
 |
physikerboard:urgestein
Gast
|
| physikerboard:urgestein Verfasst am: 16. Jan 2022 14:56 Titel: |
|
|
Es geht wohl in erster Linie um die Gesamtstrecke, die zurückgelegt wurde:
|| \, \mathrm dt )
| Zitat: | Das Fahrzeug fährt zum Zeitpunkt t = 0 los. Zu welchem Zeitpunkt T kommt es am Fuße des Berges an
(dieser befindet sich bei z = 0)? |
Hier raus müsstest du die Integrationsgrenzen bestimmen können.
|
|
|
vtxt1103
Anmeldungsdatum: 14.11.2021
Beiträge: 302
|
| vtxt1103 Verfasst am: 16. Jan 2022 14:59 Titel: |
|
|
| physikerboard:urgestein hat Folgendes geschrieben: | Es geht wohl in erster Linie um die Gesamtstrecke, die zurückgelegt wurde:
| Zitat: | Das Fahrzeug fährt zum Zeitpunkt t = 0 los. Zu welchem Zeitpunkt T kommt es am Fuße des Berges an
(dieser befindet sich bei z = 0)? |
Hier raus müsstest du die Integrationsgrenzen bestimmen können. |
Ich kann ja aber schlecht die untere grenze als t = 0 und die obere als z = 0 setzen oder ?
|
|
|
physikerboard_urgestein
Gast
|
| physikerboard_urgestein Verfasst am: 16. Jan 2022 15:03 Titel: |
|
|
Mit z ist  _z ) gemeint. Daraus kannst du die obere Grenze ausrechnen
|
|
|
vtxt1103
Anmeldungsdatum: 14.11.2021
Beiträge: 302
|
| vtxt1103 Verfasst am: 16. Jan 2022 15:17 Titel: |
|
|
| physikerboard_urgestein hat Folgendes geschrieben: | | Mit z ist gemeint. Daraus kannst du die obere Grenze ausrechnen |
Alles klar also wenn ich den vektor nach der zeit ableite erhalte ich für die z komponente  Somit müsste das ja dei obere grenze und 0 die untere grenze sein richtig? Jetzt verstehe ich auch warum man integriert um von der geschwindigkeit zur strecke zu kommen, aber müsste ich nicht jede komponente einzelt integrieren bzw wie würden dann das Integral aussehen ?
|
|
|
physikerboar__urgestein
Gast
|
| physikerboar__urgestein Verfasst am: 16. Jan 2022 15:29 Titel: |
|
|
Nicht ableiten, einfach mit null gleichsetztn.
Die Komponenten sollen nicht einzeln integriert werden, weil es zu jedem Zeitpunkt auf den Betrag der Geschwindigkeit ankommt.
^T ) soll den Streckenbeitrag  liefern, nicht  . Sonst hättest du je nach willkürlicher Wahl des Koordinatensystems andere Strecken. Die Strecke soll aber insbesondere Rotationsinvariant sein.
|
|
|
vtxt1103
Anmeldungsdatum: 14.11.2021
Beiträge: 302
|
| vtxt1103 Verfasst am: 16. Jan 2022 16:00 Titel: |
|
|
Alles klar wenn ich die z komponente gleich null setze erhalte ich für t  Somit wäre die untere grenze null, die obere grenze  aber wie wie sieht nun das innere des integrals aus?
|
|
|
physikerboard_urgestein
Gast
|
| physikerboard_urgestein Verfasst am: 16. Jan 2022 16:04 Titel: |
|
|
der Integrand besteht wue beschrieben aus der Norm der Geshwindigkeit.
1. Ortskurve nach Zeit ableiten
2. von dem Ergebnis den Betrag bilden
3. Umformen, um eine Form zu erhalten die den von dir angegebenen Hinweis anwenden lässt
|
|
|
vtxt1103
Anmeldungsdatum: 14.11.2021
Beiträge: 302
|
| vtxt1103 Verfasst am: 16. Jan 2022 16:08 Titel: |
|
|
| physikerboard_urgestein hat Folgendes geschrieben: | der Integrand besteht wue beschrieben aus der Norm der Geshwindigkeit.
1. Ortskurve nach Zeit ableiten
2. von dem Ergebnis den Betrag bilden
3. Umformen, um eine Form zu erhalten die den von dir angegebenen Hinweis anwenden lässt |
Alles klar, ich glaube ich verstehe nun was gemeint ist
|
|
|
vtxt1103
Anmeldungsdatum: 14.11.2021
Beiträge: 302
|
| vtxt1103 Verfasst am: 16. Jan 2022 18:56 Titel: |
|
|
| physikerboard_urgestein hat Folgendes geschrieben: | der Integrand besteht wue beschrieben aus der Norm der Geshwindigkeit.
1. Ortskurve nach Zeit ableiten
2. von dem Ergebnis den Betrag bilden
3. Umformen, um eine Form zu erhalten die den von dir angegebenen Hinweis anwenden lässt |
Ich habe mal angefangen, aber ab jetzt komme ich nicht mehr weiter, ich weiß nicht wie ich das auf die form des hinweises bringen soll bzw was nun der nächste schritt wäre
Im Anhang siehst du was ich bis jetzt gemacht habe
| Beschreibung: |
|
Download |
| Dateiname: |
0001.jpg |
| Dateigröße: |
605.76 KB |
| Heruntergeladen: |
91 mal |
|
|
|
physikerboar:urgestein
Gast
|
| physikerboar:urgestein Verfasst am: 16. Jan 2022 19:59 Titel: |
|
|
Es soll nach t integriert werden, nicht alpha. Du hast dann nur den Wurzelausdruck, also C=1, D=0.
Für die die variable Schneehöhe hat man dann m.E. den Ausdruck der Ordnung x^(3/2)
|
|
|
vtxt1103
Anmeldungsdatum: 14.11.2021
Beiträge: 302
|
| vtxt1103 Verfasst am: 16. Jan 2022 20:05 Titel: |
|
|
| physikerboar:urgestein hat Folgendes geschrieben: | Es soll nach t integriert werden, nicht alpha. Du hast dann nur den Wurzelausdruck, also C=1, D=0.
Für die die variable Schneehöhe hat man dann m.E. den Ausdruck der Ordnung x^(3/2) |
Wenn ich nach t umforme erhalte ich ja alpha / H somit muss dass ja die Obere grenze sein ?
Dann ist der Wurzelausdruck ja der Integrand, aber dass mit dem x^3/2 und dem was du zur oberen grenze gesagt hast, ist mir noch etwas unklar,
zumal ich nicht wüsste ich die höhe der Schneeschicht einbauen soll, außerdem spielt die Schneeschicht ja beim ersten teil der Aufgabe doch keine rolle, erst naher wenn nach der Abhängigkeit der Schneeschicht gefragt wird also h(z)
|
|
|
vtxt1103
Anmeldungsdatum: 14.11.2021
Beiträge: 302
|
| vtxt1103 Verfasst am: 16. Jan 2022 20:19 Titel: |
|
|
| physikerboar:urgestein hat Folgendes geschrieben: | Es soll nach t integriert werden, nicht alpha. Du hast dann nur den Wurzelausdruck, also C=1, D=0.
Für die die variable Schneehöhe hat man dann m.E. den Ausdruck der Ordnung x^(3/2) |
Außerdem kann D doch nicht null sein, da im Hinweis ja steht, dass die konstanten A;B;C;D positiv sein müssen
|
|
|
gast_free
Anmeldungsdatum: 15.07.2021
Beiträge: 195
|
| gast_free Verfasst am: 17. Jan 2022 14:29 Titel: |
|
|
=\alpha\cdot t)
=\frac{2}{3}\cdot \beta\cdot t^{\frac{3}{2}})
=H-x(t)=H-\alpha\cdot t)
\cdot dt^2)
Berechnung der Zeit T:
=H-\alpha\cdot t)
Berechnung der Strecke:
\cdot dt^2)
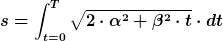
^3}]_{t=0}^{T})
^3}]-[\sqrt{8\cdot \alpha^6}]])
^3}-\sqrt{8\cdot \alpha^6}])
^3}-\sqrt{8\cdot \alpha^6}])
Berechnung des Volumens bei konstanter Räumhöhe:
---
Berechnung des Volumens bei variabler Räumhöhe:
=\frac{h_0}{H}\cdot z)
=\frac{h_0}{H}\cdot (H-\alpha\cdot t))
=b\cdot h(t)\cdot ds=b\cdot h(t)\cdot \sqrt{2\cdot \alpha^2+\beta^2\cdot t}\cdot dt)
=b\cdot h(t)\cdot ds=b\cdot \frac{h_0}{H}\cdot [(H-\alpha\cdot t)\cdot \sqrt{2\cdot \alpha^2+\beta^2\cdot t}]\cdot dt)
=b\cdot \frac{h_0}{H}\cdot \int_{t=0}^{T}[(H-\alpha\cdot t)\cdot \sqrt{2\cdot \alpha^2+\beta^2\cdot t}]\cdot dt)
|
|
|
vtxt1103
Anmeldungsdatum: 14.11.2021
Beiträge: 302
|
| vtxt1103 Verfasst am: 17. Jan 2022 15:56 Titel: |
|
|
|
Wow okay, vielen vielen dank, wobei ich die letzte Rechnung nicht so ganz nachvollziehen kann
|
|
|
|
Registrieren
Login
FAQ
Suchen
