| Autor |
Nachricht |
Corbi
Anmeldungsdatum: 17.07.2018
Beiträge: 296
|
 Corbi Verfasst am: 15. Dez 2020 17:30 Titel: Allgemein kovariante Wellengleichung Corbi Verfasst am: 15. Dez 2020 17:30 Titel: Allgemein kovariante Wellengleichung |
 |
|
Die allgmein kovariante, homogene Wellengleichung lautet:
=0)
Wobei nabla die kovariante Ableitung auf einer riemannschen Mannigfaltigkeit mit Levi-Civita-Zsmh darstellt.
macht es nun einen Unterschied ob man es so:
=g^{\mu \nu}\nabla_{\mu}\partial_{\nu}\psi(x)=g^{\mu \nu}(\partial_{\mu}\partial_{\nu}-\Gamma^{\rho}_{\mu \nu}\partial_{\rho})\psi(x)=0)
oder so:
=(\partial_{\mu}\partial^{\nu}+\Gamma^{\mu}_{\mu \nu}\partial^{\nu})\psi(x)=(g^{\mu \nu}\partial_{\nu}\partial_{\mu}+\partial_{\mu}(g^{\mu \nu})\partial_{\nu}+\Gamma^{\mu}_{\mu \nu}\partial^{\nu})\psi(x)=0)
aufdröselt?
Eigentlich sollte es ja identisch sein, ganz sicher bin ich mir aber nicht |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18062
|
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 15. Dez 2020 22:15 Titel: Re: Allgemein kovariante Wellengleichung index_razor Verfasst am: 15. Dez 2020 22:15 Titel: Re: Allgemein kovariante Wellengleichung |
 |
|
| Corbi hat Folgendes geschrieben: |
macht es nun einen Unterschied ob man es so:
=g^{\mu \nu}\nabla_{\mu}\partial_{\nu}\psi(x)=g^{\mu \nu}(\partial_{\mu}\partial_{\nu}-\Gamma^{\rho}_{\mu \nu}\partial_{\rho})\psi(x)=0)
oder so:
=(\partial_{\mu}\partial^{\nu}+\Gamma^{\mu}_{\mu \nu}\partial^{\nu})\psi(x)=(g^{\mu \nu}\partial_{\nu}\partial_{\mu}+\partial_{\mu}(g^{\mu \nu})\partial_{\nu}+\Gamma^{\mu}_{\mu \nu}\partial^{\nu})\psi(x)=0)
aufdröselt?
|
Die erste Variante sieht korrekt aus. Aber in der zweiten stimmt irgendwas nicht. Bereits nach dem ersten "=" ist das Indexbild verunglückt. Mir ist auch auf Anhieb nicht klar, wie es gemeint sein könnte. |
|
 |
Corbi
Anmeldungsdatum: 17.07.2018
Beiträge: 296
|
 Corbi Verfasst am: 15. Dez 2020 22:39 Titel: Re: Allgemein kovariante Wellengleichung Corbi Verfasst am: 15. Dez 2020 22:39 Titel: Re: Allgemein kovariante Wellengleichung |
 |
|
| index_razor hat Folgendes geschrieben: |
Die erste Variante sieht korrekt aus. Aber in der zweiten stimmt irgendwas nicht. Bereits nach dem ersten "=" ist das Indexbild verunglückt. Mir ist auch auf Anhieb nicht klar, wie es gemeint sein könnte. |
Oh ja es soll natürlich heißen:
=(\partial_{\mu}\partial^{\mu}+\Gamma^{\mu}_{\mu \nu}\partial^{\nu})\psi(x)=(g^{\mu \nu}\partial_{\nu}\partial_{\mu}+\partial_{\mu}(g^{\mu \nu})\partial_{\nu}+\Gamma^{\mu}_{\mu \nu}\partial^{\nu})\psi(x)=0)
hinter dem zweiten Gleichheitszeichen habe ich die  eingesetzt und dann die Produktregel verwendet. eingesetzt und dann die Produktregel verwendet.
So stimmt es dann auch mit der Variante von TomS überein....kann man denn auch die inverse Metrik immer vor die kovariante Ableitung ziehen? |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18062
|
 TomS Verfasst am: 15. Dez 2020 23:13 Titel: TomS Verfasst am: 15. Dez 2020 23:13 Titel: |
 |
|
Ja.
Ein allgemeiner Zusammenhang (= eine allgemeine kovariante Ableitung) heißt metrischer Zusammenhang, wenn die Metrik kovariant konstant (bezüglich dieser kovarianten Ableitung) ist. Das ist für den Levi-Civita-Zusammenhang der Fall.

Dies ist eine allgemeine geometrische Eigenschaft, unabhängig von ko- oder kontravarianten Komponenten.
https://en.wikipedia.org/wiki/Levi-Civita_connection
https://en.wikipedia.org/wiki/Fundamental_theorem_of_Riemannian_geometry
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 16. Dez 2020 18:41 Titel: Re: Allgemein kovariante Wellengleichung index_razor Verfasst am: 16. Dez 2020 18:41 Titel: Re: Allgemein kovariante Wellengleichung |
 |
|
| Corbi hat Folgendes geschrieben: |
Oh ja es soll natürlich heißen:
=(\partial_{\mu}\partial^{\mu}+\Gamma^{\mu}_{\mu \nu}\partial^{\nu})\psi(x)=(g^{\mu \nu}\partial_{\nu}\partial_{\mu}+\partial_{\mu}(g^{\mu \nu})\partial_{\nu}+\Gamma^{\mu}_{\mu \nu}\partial^{\nu})\psi(x)=0)
hinter dem zweiten Gleichheitszeichen habe ich die  eingesetzt und dann die Produktregel verwendet. eingesetzt und dann die Produktregel verwendet.
So stimmt es dann auch mit der Variante von TomS überein....kann man denn auch die inverse Metrik immer vor die kovariante Ableitung ziehen? |
Kann sein, daß ich etwas übersehe. Aber wendest du die Definition nicht falsch an? Der Laplace-Operator wäre doch
f.)
Wo willst du da die Metrik vor die kovariante Ableitung ziehen? |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18062
|
 TomS Verfasst am: 16. Dez 2020 18:50 Titel: TomS Verfasst am: 16. Dez 2020 18:50 Titel: |
 |
|
 \, f = (g^{\mu\nu} \, \nabla_\nu) \, \nabla_ \mu \, f = \nabla^\mu \, ( g_{\mu\nu} \nabla^\nu) \, f )
Erstens ist die Metrik kovariant konstant und darf daher vor die kovariante Ableitung gezogen werden. Und zweitens gilt für skalare Funktionen ohnehin

_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 16. Dez 2020 19:12 Titel: index_razor Verfasst am: 16. Dez 2020 19:12 Titel: |
 |
|
| TomS hat Folgendes geschrieben: |  \, \nabla_ \mu \, f = \nabla^\mu \, ( g_{\mu\nu} \nabla^\nu) \, f )
Erstens ist die Metrik kovariant konstant und darf daher vor die kovariante Ableitung gezogen werden.
|
Was meinst du damit? Es gilt doch  . Die Metrik ist zwar kovariant konstant, aber die Metrikkoeffizienten sind normale (nichtkonstante) Funktionen. Außerdem ist deine Klammerung hier seltsam. Wir berechnen doch die zweite kovariante Ableitung von f, nicht die kovariante Ableitung der kovarianten Ableitung von f, wie deine Schreibweise hinter dem zweiten "=" suggeriert. Für mich sieht es so aus, als ob der Term . Die Metrik ist zwar kovariant konstant, aber die Metrikkoeffizienten sind normale (nichtkonstante) Funktionen. Außerdem ist deine Klammerung hier seltsam. Wir berechnen doch die zweite kovariante Ableitung von f, nicht die kovariante Ableitung der kovarianten Ableitung von f, wie deine Schreibweise hinter dem zweiten "=" suggeriert. Für mich sieht es so aus, als ob der Term  bei dir fehlt. bei dir fehlt.
| Zitat: |
Und zweitens gilt für skalare Funktionen ohnehin
 |
Ja, deswegen müßte gelten
f=g^{\mu\nu}\nabla_\mu(\partial_\nu f) - g^{\mu\nu}\nabla_{\nabla_{\nu}e_\mu}f = g^{\mu\nu}(\partial_\mu(\partial_\nu f) - \Gamma_{\mu\nu}^\lambda \partial_\lambda f))
oder nicht? Da muß man doch nirgendwo irgendwelche Metrikkoeffizienten vor die Ableitung ziehen, was ohnehin nicht so ohne weiteres geht. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 16. Dez 2020 19:30 Titel: index_razor Verfasst am: 16. Dez 2020 19:30 Titel: |
 |
|
P.S. Ich glaube wir sollten hier strenger unterscheiden zwischen Funktionen 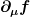 und dem Kovektor und dem Kovektor  mit den Komponenten mit den Komponenten 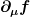 . Wenn da nur . Wenn da nur
)
steht, ist (in Physikernotation) nicht so ohne weiteres klar, was gemeint ist. (Bei mir, z.B. in meiner letzten Gleichung, bedeutet es die Ableitung der Funktion  , also , also  .) .) |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18062
|
 TomS Verfasst am: 16. Dez 2020 21:05 Titel: TomS Verfasst am: 16. Dez 2020 21:05 Titel: |
 |
|
| index_razor hat Folgendes geschrieben: | Was meinst du damit? Es gilt doch  . Die Metrik ist zwar kovariant konstant, aber die Metrikkoeffizienten sind normale (nichtkonstante) Funktionen. . Die Metrik ist zwar kovariant konstant, aber die Metrikkoeffizienten sind normale (nichtkonstante) Funktionen. |
Richtig, die kovariante Ableitung verschwindet nur bei Kontraktion; so war das gemeint.
| index_razor hat Folgendes geschrieben: | | Außerdem ist deine Klammerung hier seltsam. |
Da hast recht; deine aber auch ;-)
Es muss überall ) stehen, nicht stehen, nicht  f) . .
| index_razor hat Folgendes geschrieben: | | Da muß man doch nirgendwo irgendwelche Metrikkoeffizienten vor die Ableitung ziehen, was ohnehin nicht so ohne weiteres geht. |
Ich denke, es geht um die Anwendung der Produktregel.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 16. Dez 2020 21:15 Titel: index_razor Verfasst am: 16. Dez 2020 21:15 Titel: |
 |
|
| TomS hat Folgendes geschrieben: | | index_razor hat Folgendes geschrieben: | Was meinst du damit? Es gilt doch  . Die Metrik ist zwar kovariant konstant, aber die Metrikkoeffizienten sind normale (nichtkonstante) Funktionen. . Die Metrik ist zwar kovariant konstant, aber die Metrikkoeffizienten sind normale (nichtkonstante) Funktionen. |
Richtig, die kovariante Ableitung verschwindet nur bei Kontraktion; so war das gemeint.
|
Wieso? Die Kontraktion wäre doch  . Das ist im allgemeinen immer noch ungleich null. Ich sehe deshalb noch keine unmittelbare Rechtfertigung für diesen Schritt. Aber ich verstehe auch nicht, wozu er nötig sein sollte. Die Definition . Das ist im allgemeinen immer noch ungleich null. Ich sehe deshalb noch keine unmittelbare Rechtfertigung für diesen Schritt. Aber ich verstehe auch nicht, wozu er nötig sein sollte. Die Definition  enthält doch keine derartige Mehrdeutigkeit. enthält doch keine derartige Mehrdeutigkeit. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 16. Dez 2020 21:22 Titel: index_razor Verfasst am: 16. Dez 2020 21:22 Titel: |
 |
|
| TomS hat Folgendes geschrieben: | | index_razor hat Folgendes geschrieben: | Was meinst du damit? Es gilt doch  . Die Metrik ist zwar kovariant konstant, aber die Metrikkoeffizienten sind normale (nichtkonstante) Funktionen. . Die Metrik ist zwar kovariant konstant, aber die Metrikkoeffizienten sind normale (nichtkonstante) Funktionen. |
Richtig, die kovariante Ableitung verschwindet nur bei Kontraktion; so war das gemeint.
| index_razor hat Folgendes geschrieben: | | Außerdem ist deine Klammerung hier seltsam. |
Da hast recht; deine aber auch ;-)
Es muss überall ) stehen, nicht stehen, nicht  f) |
Das war ja nur an einer Stelle und dort war es schon Absicht. Ich wollte damit den Unterschied zwischen der zweiten kovarianten Ableitung  angewendet auf f und angewendet auf f und ) betonen. Wie würdest du das denn auseinanderhalten? betonen. Wie würdest du das denn auseinanderhalten? |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18062
|
 TomS Verfasst am: 16. Dez 2020 21:32 Titel: TomS Verfasst am: 16. Dez 2020 21:32 Titel: |
 |
|
| index_razor hat Folgendes geschrieben: | Die Kontraktion wäre doch
 . .
Das ist im allgemeinen immer noch ungleich null. |
Doch, das ist null, wenn der Zusammenhang metrik-kompatibel ist. Und das ist für eine Riemannsche Mannigfaltigkeit mit Levi-Cevita-Zusammenhang immer erfüllt.
EDIT: Es gilt sogar ohne Kontraktion, das war mit nicht mehr bewusst.
Abschnitt 5.3 in http://www.blau.itp.unibe.ch/newlecturesGR.pdf
Deshalb ist
| TomS hat Folgendes geschrieben: | | index_razor hat Folgendes geschrieben: | Was meinst du damit? Es gilt doch  . Die Metrik ist zwar kovariant konstant, aber die Metrikkoeffizienten sind normale (nichtkonstante) Funktionen. . Die Metrik ist zwar kovariant konstant, aber die Metrikkoeffizienten sind normale (nichtkonstante) Funktionen. |
Richtig, die kovariante Ableitung verschwindet nur bei Kontraktion. |
... beides falsch. Es gilt

_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 16. Dez 2020 21:58 Titel: index_razor Verfasst am: 16. Dez 2020 21:58 Titel: |
 |
|
| TomS hat Folgendes geschrieben: | | index_razor hat Folgendes geschrieben: | Die Kontraktion wäre doch
 . .
Das ist im allgemeinen immer noch ungleich null. |
Doch, das ist null, wenn der Zusammenhang metrik-kompatibel ist. Und das ist für eine Riemannsche Mannigfaltigkeit mit Levi-Cevita-Zusammenhang immer erfüllt.
EDIT: Es gilt sogar ohne Kontraktion, das war mit nicht mehr bewusst.
Abschnitt 5.3 in http://www.blau.itp.unibe.ch/newlecturesGR.pdf
Deshalb ist
| TomS hat Folgendes geschrieben: | | index_razor hat Folgendes geschrieben: | Was meinst du damit? Es gilt doch  . Die Metrik ist zwar kovariant konstant, aber die Metrikkoeffizienten sind normale (nichtkonstante) Funktionen. . Die Metrik ist zwar kovariant konstant, aber die Metrikkoeffizienten sind normale (nichtkonstante) Funktionen. |
Richtig, die kovariante Ableitung verschwindet nur bei Kontraktion. |
... beides falsch. Es gilt
 |
Unter  verstehe ich die Funktion verstehe ich die Funktion  = g_x(\partial_\mu(x), \partial_\nu(x))) . Du hattest oben selbst geschrieben, daß für Funktionen . Du hattest oben selbst geschrieben, daß für Funktionen
 . .
Wenn man hier  einsetzt, ist das i.a. nicht null, auch nicht nach Kontraktion. einsetzt, ist das i.a. nicht null, auch nicht nach Kontraktion.
Von irgendeiner dieser Definitionen weichst du jetzt offenbar ab. Kann es sein, daß du mit  jetzt einfach jetzt einfach
_{\nu\lambda})
in Physikernotation meinst? Wenn ja, dann ist das zwar null, es widerspricht aber m.E. deiner Verwendung von  weiter oben im thread. Aus diesem Grund glaube ich, daß wir bei dieser Unterscheidung präziser sein müssen. weiter oben im thread. Aus diesem Grund glaube ich, daß wir bei dieser Unterscheidung präziser sein müssen. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 16. Dez 2020 22:02 Titel: index_razor Verfasst am: 16. Dez 2020 22:02 Titel: |
 |
|
| index_razor hat Folgendes geschrieben: | Kann es sein, daß du mit  jetzt einfach jetzt einfach
_{\nu\lambda})
in Physikernotation meinst? |
Das ist übrigens definitiv auch die Definition die das Skript benutzt, auf das du verlinkt hattest. (Siehe Gl. 5.38. Auf der linken Seite steht zwar  . Auf der rechten Seite steht aber der Ausdruck für . Auf der rechten Seite steht aber der Ausdruck für _{\nu\lambda}) .) .) |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18062
|
 TomS Verfasst am: 16. Dez 2020 22:07 Titel: TomS Verfasst am: 16. Dez 2020 22:07 Titel: |
 |
|
| index_razor hat Folgendes geschrieben: | [Du hattest oben selbst geschrieben, daß für Funktionen
 . .
Wenn man hier  einsetzt, ist das i.a. nicht null, auch nicht nach Kontraktion. einsetzt, ist das i.a. nicht null, auch nicht nach Kontraktion. |
f ist eine skalare Funktion. Da kannst du nicht einfach den metrischen Tensor einsetzen.
| index_razor hat Folgendes geschrieben: | | Von irgendeiner dieser Definitionen weichst du jetzt offenbar ab. |
Schauen wir‘s uns gerne nochmal an.
Jedenfalls ist
- die kovariante Ableitung des metrischen Tensors Null - siehe o.g. Quelle
- die kovariante Ableitung einer skalaren Funktion gleich deren partieller Ableitung
- die Produktregel für die kovariante Ableitung gültig
Daraus folgt der Laplacian auf eine skalare Funktion als Laplace-Beltrami-Operator - siehe mein erster Beitrag.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 16. Dez 2020 22:15 Titel: index_razor Verfasst am: 16. Dez 2020 22:15 Titel: |
 |
|
| TomS hat Folgendes geschrieben: | | index_razor hat Folgendes geschrieben: | [Du hattest oben selbst geschrieben, daß für Funktionen
 . .
Wenn man hier  einsetzt, ist das i.a. nicht null, auch nicht nach Kontraktion. einsetzt, ist das i.a. nicht null, auch nicht nach Kontraktion. |
f ist eine skalare Funktion. Da kannst du nicht einfach den metrischen Tensor einsetzen.
|
Tue ich auch nicht. Ich setze eine Komponente  des metrischen Tensors ein. Das ist eine Funktion und ich habe dies auch konsequent als solche verwendet. Und wegen der Verwechslungsgefahr in Physikernotation betone ich ja gerade diesen Unterschied. des metrischen Tensors ein. Das ist eine Funktion und ich habe dies auch konsequent als solche verwendet. Und wegen der Verwechslungsgefahr in Physikernotation betone ich ja gerade diesen Unterschied.
| Zitat: |
| index_razor hat Folgendes geschrieben: | | Von irgendeiner dieser Definitionen weichst du jetzt offenbar ab. |
Schauen wir‘s uns gerne nochmal an.
Jedenfalls ist
- die kovariante Ableitung des metrischen Tensors Null - siehe o.g. Quelle
- die kovariante Ableitung einer skalaren Funktion gleich deren partieller Ableitung
- die Produktregel für die kovariante Ableitung gültig
Daraus sollte der Laplacian auf eine skalare Funktion als Laplace-Beltrami-Operator folgen - siehe mein erster Beitrag. |
Genau die Definition aus dem ersten Wikipedia-Link habe ich wortwörtlich angewendet:
f)
(Definitionen wie oben.) Was ich nicht verstehe ist, wo man da Metrikkoeffizienten an kovarianten Ableitungen vorbeiziehen soll und wieso das überhaupt erlaubt sein sollte. Aus der kovarianten Konstanz von 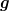 folgt das m.E. nicht und man benötigt sie auch nicht, soweit ich sehe. folgt das m.E. nicht und man benötigt sie auch nicht, soweit ich sehe.
P.S. du mußt mir übrigens nicht belegen, daß die Metrik kovariant konstant ist. Das bestreite ich gar nicht. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18062
|
 TomS Verfasst am: 17. Dez 2020 11:18 Titel: TomS Verfasst am: 17. Dez 2020 11:18 Titel: |
 |
|
| index_razor hat Folgendes geschrieben: | | TomS hat Folgendes geschrieben: | | index_razor hat Folgendes geschrieben: | [Du hattest oben selbst geschrieben, daß für Funktionen
 . .
Wenn man hier  einsetzt, ist das i.a. nicht null, auch nicht nach Kontraktion. einsetzt, ist das i.a. nicht null, auch nicht nach Kontraktion. |
f ist eine skalare Funktion. Da kannst du nicht einfach den metrischen Tensor einsetzen.
|
Tue ich auch nicht. Ich setze eine Komponente  des metrischen Tensors ein. Das ist eine Funktion und ich habe dies auch konsequent als solche verwendet. des metrischen Tensors ein. Das ist eine Funktion und ich habe dies auch konsequent als solche verwendet. |
Aber das darfst du nicht.
Ich schrieb, f ist eine skalare Funktion. Dann und nur dann reduziert sich die Definition der kovarianten Ableitung auf die partielle Ableitung.
Wenn du stattdessen die Komponenten des metrischen Tensors einsetzt, liegt keine skalare Funktion vor. Die kovarianten Ableitung bleibt einschließlich Christoffel-Symbol erhalten, und das Ergebnis Null folgt mittels der Definition der Christoffel-Symbole durch explizite Rechnung.
Die Gleichheitszeichen bedeuten jeweils etwas anderes - Definition bzw. explizite Rechnung.
| index_razor hat Folgendes geschrieben: | Genau die Definition aus dem ersten Wikipedia-Link habe ich wortwörtlich angewendet:
f)
(Definitionen wie oben.) Was ich nicht verstehe ist, wo man da Metrikkoeffizienten an kovarianten Ableitungen vorbeiziehen soll und wieso das überhaupt erlaubt sein sollte. Aus der kovarianten Konstanz von 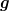 folgt das m.E. nicht und man benötigt sie auch nicht, soweit ich sehe. folgt das m.E. nicht und man benötigt sie auch nicht, soweit ich sehe. |
Nach der Definition benötigst du das natürlich nicht.
Wenn du aber mit

rechnest, muss doch das selbe herauskommen. Und dann wirkt die linke kovariante Ableitung gemäß Produktregel einmal auf die Metrik alleine und einmal auf den Vierervektor rechts von der Metrik.
Oder nicht?
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 17. Dez 2020 12:37 Titel: index_razor Verfasst am: 17. Dez 2020 12:37 Titel: |
 |
|
| TomS hat Folgendes geschrieben: | | index_razor hat Folgendes geschrieben: | | TomS hat Folgendes geschrieben: | | index_razor hat Folgendes geschrieben: | [Du hattest oben selbst geschrieben, daß für Funktionen
 . .
Wenn man hier  einsetzt, ist das i.a. nicht null, auch nicht nach Kontraktion. einsetzt, ist das i.a. nicht null, auch nicht nach Kontraktion. |
f ist eine skalare Funktion. Da kannst du nicht einfach den metrischen Tensor einsetzen.
|
Tue ich auch nicht. Ich setze eine Komponente  des metrischen Tensors ein. Das ist eine Funktion und ich habe dies auch konsequent als solche verwendet. des metrischen Tensors ein. Das ist eine Funktion und ich habe dies auch konsequent als solche verwendet. |
Aber das darfst du nicht.
Ich schrieb, f ist eine skalare Funktion. Dann und nur dann reduziert sich die Definition der kovarianten Ableitung auf die partielle Ableitung.
|
Nein, das siehst du falsch. Der affine Zusammenhang als Operator einer Tensorableitung macht keinen Unterschied zwischen "skalaren" und "nichtskalaren" Funktionen. (Abgesehen davon, daß dieser Unterschied mathematisch schlecht definiert ist.)
Es gilt einfach ) für jede Funktion f. Das gilt auch für Koordinatenfunktionen für jede Funktion f. Das gilt auch für Koordinatenfunktionen
 = u^\mu)
oder für Funktionen, die man (zufällig) als Komponenten von Tensoren verwendet. Tatsächlich leitet man auf diese Art die Komponenten der kovarianten Ableitung eines Vektors her
 = (\nabla_\mu v^i)e_i + v^i \nabla_\mu e_i = (\partial_\mu v^i + v^k\Gamma_{k\mu}^i)e_i = (\nabla_\mu v)^i e_i)
Hier benutzt man explizit  obwohl obwohl  vermutlich keine "skalare" Funktion ist nach deiner Auffassung. vermutlich keine "skalare" Funktion ist nach deiner Auffassung.
| Zitat: |
Wenn du stattdessen die Komponenten des metrischen Tensors einsetzt, liegt keine skalare Funktion vor. Die kovarianten Ableitung bleibt einschließlich Christoffel-Symbol erhalten, und das Ergebnis Null folgt mittels der Definition der Christoffel-Symbole durch explizite Rechnung.
Die Gleichheitszeichen bedeuten jeweils etwas anderes.
|
Nein, das stimmt so einfach nicht. Ich denke du verwechselst immer noch die Komponenten der kovarianten Ableitung _{\mu\lambda}) (die tatsächlich null sind, wegen der kovarianten Konstanz des Tensors g) mit der kovarianten Ableitung (die tatsächlich null sind, wegen der kovarianten Konstanz des Tensors g) mit der kovarianten Ableitung  einer Komponentenfunktion von g, was etwas völlig anderes ist, nämlich einfach einer Komponentenfunktion von g, was etwas völlig anderes ist, nämlich einfach  . Die Komponenten . Die Komponenten  sind alles andere als kovariant Konstant. sind alles andere als kovariant Konstant.
Viele Physiktexte, inklusive des Skripts, auf das du weiter oben verlinkt hast, führen eine Notation ein, mit der man beides unmöglich unterscheiden kann. Das führt leicht zu Verwirrung und Mißverständnissen so wie hier. Diesem Problem gehen die Autoren normalerweise aus dem Weg, indem sie niemals kovariante Ableitung explizit auf eine Funktion (egal ob "skalar" oder nicht) anwenden, sondern stattdessen immer gleich 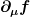 schreiben. Eine Grundeigenschaft der kovarianten Ableitung ist also in dieser Notation gar nicht formulierbar. Deswegen finde ich sie unvorteilhaft. schreiben. Eine Grundeigenschaft der kovarianten Ableitung ist also in dieser Notation gar nicht formulierbar. Deswegen finde ich sie unvorteilhaft.
| Zitat: |
| index_razor hat Folgendes geschrieben: | Genau die Definition aus dem ersten Wikipedia-Link habe ich wortwörtlich angewendet:
f)
(Definitionen wie oben.) Was ich nicht verstehe ist, wo man da Metrikkoeffizienten an kovarianten Ableitungen vorbeiziehen soll und wieso das überhaupt erlaubt sein sollte. Aus der kovarianten Konstanz von 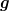 folgt das m.E. nicht und man benötigt sie auch nicht, soweit ich sehe. folgt das m.E. nicht und man benötigt sie auch nicht, soweit ich sehe. |
Nach der Definition muss du das natürlich nicht.
Wenn du aber mit

rechnest, muss doch das selbe herauskommen. Und dann wirkt die linke kovariante Ableitung gemäß Produktregel einmal auf die Metrik alleine und einmal auf den Vierervektor rechts von der Metrik.
Oder nicht? |
Das ist im Prinzip der Hintergrund meiner Frage. Ich bin nicht sicher daß dasselbe rauskommt oder rauskommen muß. Zum Teil liegt das aber daran, daß die Notation so mehrdeutig ist, und ich nicht immer weiß was gemeint ist. Die Mehrdeutigkeiten scheinen manchmal weder Corbi noch dir bewußt zu sein.
Nehmen wir zum Beispiel  . Was bedeutet das? Normalerweise ist . Was bedeutet das? Normalerweise ist  die kovariante Ableitung in Richtung des Basisvektors die kovariante Ableitung in Richtung des Basisvektors  . Wenn ich dies auf eine Funktion anwende, erhalte ich lediglich eine weitere Funktion, nämlich . Wenn ich dies auf eine Funktion anwende, erhalte ich lediglich eine weitere Funktion, nämlich 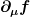 . Die Ableitung dieser Funktion in Richtung . Die Ableitung dieser Funktion in Richtung  ergäbe einfach ergäbe einfach  , also stünde da , also stünde da  was nicht gemeint sein kann. was nicht gemeint sein kann.
Tatsächlich meinen Physiker, wenn sie  schreiben, fast immer die schreiben, fast immer die 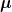 -Komponente der Ableitung von -Komponente der Ableitung von  , also , also
 = (\partial_\nu f_\mu - \Gamma^\lambda_{\mu\nu}f_\lambda )\dd x^\mu.)
Damit ergäbe sich für 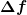 , wiederum derselbe Ausdruck, wie nach der Definition , wiederum derselbe Ausdruck, wie nach der Definition  (X,Y) = \nabla_Y(\nabla_Y f) - \nabla_{\nabla_Y X}f) , was natürlich kein Zufall ist. Die zweite kovariante Ableitung von f ist definiert als kovariante Ableitung von , was natürlich kein Zufall ist. Die zweite kovariante Ableitung von f ist definiert als kovariante Ableitung von  . .
Damit wird dann klar, daß  nicht nicht ) bedeuten kann, sondern nur bedeuten kann, sondern nur
(e_\mu,g^{\mu\nu} e_\nu)) . Die einzige Möglichkeit hier die Metrik an eine andere Stelle zu schreiben, lautet . Die einzige Möglichkeit hier die Metrik an eine andere Stelle zu schreiben, lautet (g^{\mu\nu}e_\mu, e_\nu)) was dasselbe ergibt. Aber niemals wandern die Metrikkoeffizienten dabei unter eine der Ableitungen. Sie stehen immer in einem Tensorslot des gesamten Ausdrucks. Da Tensoren lokale Objekte sind, entstehen dadurch niemals Ableitungen von was dasselbe ergibt. Aber niemals wandern die Metrikkoeffizienten dabei unter eine der Ableitungen. Sie stehen immer in einem Tensorslot des gesamten Ausdrucks. Da Tensoren lokale Objekte sind, entstehen dadurch niemals Ableitungen von  . Das ganze hat also mit der kovarianten Konstanz von g nichts zu tun, sondern lediglich mit dem Tensorcharakter von . Das ganze hat also mit der kovarianten Konstanz von g nichts zu tun, sondern lediglich mit dem Tensorcharakter von  . .
Nun kann man natürlich die Frage stellen: kommt trotzdem dasselbe raus, wenn ich die kovariante Ableitung statt von 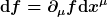 von von  bilde? Auf Anhieb wüßte ich keinen Grund, warum das so sein sollte. Ich berechne ja zunächst mal die kovariante Ablleitung eines anderen Objekts. bilde? Auf Anhieb wüßte ich keinen Grund, warum das so sein sollte. Ich berechne ja zunächst mal die kovariante Ablleitung eines anderen Objekts.
Aber selbst wenn dasselbe rauskäme. Mein Punkt ist der, daß die Definition 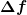 keinerlei Mehrdeutigkeit enthält. Man muß also gar nicht beweisen, daß hier zwei Wege zum selben Ergebnis führen. Viel wichtiger ist, glaube ich, daß man sich klar macht, welche Operationen hier auf welche Objekte angewendet werden. Es geht hier nicht in erster Linie im ein mathematisches Problem, sondern um eines der Notation. keinerlei Mehrdeutigkeit enthält. Man muß also gar nicht beweisen, daß hier zwei Wege zum selben Ergebnis führen. Viel wichtiger ist, glaube ich, daß man sich klar macht, welche Operationen hier auf welche Objekte angewendet werden. Es geht hier nicht in erster Linie im ein mathematisches Problem, sondern um eines der Notation.
Zuletzt bearbeitet von index_razor am 17. Dez 2020 12:59, insgesamt einmal bearbeitet |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18062
|
 TomS Verfasst am: 17. Dez 2020 12:56 Titel: TomS Verfasst am: 17. Dez 2020 12:56 Titel: |
 |
|
Grundsätzlich stimme ich dir zu, dass die Notation nicht geeignet ist, diese Unterschiede darzustellen.
Ich denke jedoch, die Notation ist insofern nützlich, als sie in Fällen angewendet wird, wo diese Unterschiede fapp irrelevant sind. Mir ist jedenfalls noch kein Gegenbeispiel über den Weg gelaufen.
D.h. ich gehe tatsächlich davon aus, dass beide Methoden zum selben Ergebnis führen, denn ansonsten wäre die Notation zumindest an dieser Stelle - falsch.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 17. Dez 2020 13:07 Titel: index_razor Verfasst am: 17. Dez 2020 13:07 Titel: |
 |
|
| TomS hat Folgendes geschrieben: |
D.h. ich gehe tatsächlich davon aus, dass beide Methoden zum selben Ergebnis führen, denn ansonsten wäre die Notation zumindest an dieser Stelle - falsch. |
Bis jetzt bin ich nicht mal sicher, daß es sich hier um zwei "Methoden" handelt dasselbe auszurechnen oder um zwei verschiedene Objekte, die berechnet werden. Weder von dir noch von Corbi liegt dafür m.E. eine hinreichend genaue Definition vor, was die verwendeten Ausdrücke im Einzelfall bedeuten. Auf mehrere Mehrdeutigkeiten habe ich ja hingewiesen. Diejenigen Interpretationen, die mit der geometrischen Definition übereinstimmen, ergeben alle trivialerweise dasselbe. Und dies wäre übrigens, soweit ich sehe, auch der Fall, wenn es sich nicht um den Levi-Civita-Zusammenhang handelte. Also hat es m.E. nichts mit der kovarianten Konstanz von g zu tun.
Wenn es sich einfach um zwei verschiedene Objekte handelt, kann ja auch nicht dasselbe herauskommen. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18062
|
 TomS Verfasst am: 20. Dez 2020 08:30 Titel: TomS Verfasst am: 20. Dez 2020 08:30 Titel: |
 |
|
Ich fasse das nochmal zusammen.
Die Formeln stammen aus alten Skripten, man findet sie jedoch auch im Netz, z.B. bei Carroll.
(1) kovariante Ableitung
)
)
)
(2) Metrik-Verträglichkeit
)
)
 )
Daraus folgt auch außerdem
 = \nabla_\nu V_\mu )
(3) Kontraktion
 )
 \qquad (3b) )
(4) Laplace-Beltrami
 )
 \qquad (4b) )
wobei (b) wegen Produktregel und Metrik-Kompatibilität gilt (du darfst mir gerne erklären, warum; ich sehe jedoch nichts, was in der üblichen Index-Notation der Physiker dagegen spräche)
(5) Ableitung der Determinante
 g^{\mu\nu} \sqrt{|g|} \qquad (5))
(6) Damit folgt die Identität beider Darstellungen des Laplace-Beltrami-Operators „von links nach rechts“ mittels direkter Berechnung unter Verwendung der Metrik-Verträglichkeit des Levi-Civita-Zusammenhangs
 = \ldots \left( (\partial_\mu g^{\mu\nu}) + \frac{1}{2} g^{\mu\nu} (\partial_\mu g_{\lambda\rho}) g^{\lambda\rho} + g^{\mu\nu} \partial_\mu \right) \partial_\nu f = \ldots = g^{\mu\nu} \nabla_\mu \partial_\nu f = \nabla^2 f )
| index_razor hat Folgendes geschrieben: | | Weder von dir noch von Corbi liegt dafür m.E. eine hinreichend genaue Definition vor, was die verwendeten Ausdrücke im Einzelfall bedeuten. |
Du kannst es auch künstlich kompliziert machen. Im Rahmen der Physik reichen die Rechenregeln m.E. aus.
| index_razor hat Folgendes geschrieben: | | Diejenigen Interpretationen, die mit der geometrischen Definition übereinstimmen, ergeben alle trivialerweise dasselbe. Und dies wäre übrigens, soweit ich sehe, auch der Fall, wenn es sich nicht um den Levi-Civita-Zusammenhang handelte. Also hat es m.E. nichts mit der kovarianten Konstanz von g zu tun. |
In meinen Rechnungen sowie in allen Quellen, die ich gefunden habe, werden immer spezielle Eigenschaften des Levi-Civita-Zusammenhang verwendet.
Aus
https://en.m.wikipedia.org/wiki/Laplace%E2%80%93Beltrami_operator#Tensor_Laplacian
https://en.m.wikipedia.org/wiki/Hessian_matrix#Generalizations_to_Riemannian_manifolds
folgt dies alles zunächst nur für den Levi-Civita-Zusammenhang.
Hier
https://en.m.wikipedia.org/wiki/Laplace_operators_in_differential_geometry#Connection_Laplacian
finde ich explizit „ If the connection of interest is the Levi-Civita connection one can find a convenient formula for the Laplacian of a scalar function ...“ was auf (6), gelesen „von rechts nach links“ hinausläuft.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 20. Dez 2020 09:48 Titel: index_razor Verfasst am: 20. Dez 2020 09:48 Titel: |
 |
|
| TomS hat Folgendes geschrieben: |
(2) Metrik-Verträglichkeit
)
)
|
Schreibe hierfür doch mal, so wie es korrekt wäre, ^{\mu\nu} = 0) und verwende diese Form in der Spur der zweiten kovarianten Ableitung. Bis jetzt sieht es nicht so aus, als würdest du überhaupt anerkennen, daß hier ein wesentlicher Unterschied besteht. Solange wir darüber nicht einig sind, bringen deine Formelsammlungen nichts. und verwende diese Form in der Spur der zweiten kovarianten Ableitung. Bis jetzt sieht es nicht so aus, als würdest du überhaupt anerkennen, daß hier ein wesentlicher Unterschied besteht. Solange wir darüber nicht einig sind, bringen deine Formelsammlungen nichts.
| Zitat: |
(4) Laplace-Beltrami
 )
 \qquad (4b) )
wobei (b) mittels Produktregel und Metrik-Kompatibilität folgt
|
Wieso soll das folgen? (4a) ist doch nur eine Schreibweise für die Spur des Tensors  . (Offensichtlich bezeichnest du jetzt diese Spur bereits als " . (Offensichtlich bezeichnest du jetzt diese Spur bereits als " " was die nächste Mehrdeutigkeit einführt. Oder war das ein Versehen?) " was die nächste Mehrdeutigkeit einführt. Oder war das ein Versehen?)
Jedenfalls ist diese Spurbildung mittels Metrik eine rein algebraische Operation. Die  sind hier allerdings Funktionen auf der Raumzeit. Wieso du die unter die Ableitung ziehen willst, geschweige denn ziehen kannst, hast du immer noch nicht erklärt. Für die Funktionen sind hier allerdings Funktionen auf der Raumzeit. Wieso du die unter die Ableitung ziehen willst, geschweige denn ziehen kannst, hast du immer noch nicht erklärt. Für die Funktionen 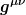 gilt nämlich gilt nämlich ^{\mu\nu}=0)
Die linke Gl. gilt hier nach deiner Bedingung (1a). Die rechte Gl. bedeutet etwas völlig anderes und ist die korrekte Formulierung von deiner Bedingung (2b).
Ich sprach von der Beziehung  - \Gamma_{\mu\nu}^\lambda \partial_\lambda f)) . .
Der Tensor  (X,Y) = \nabla_Y(\nabla_X f) - \nabla_{\nabla_Y X}f) benötigt offensichtlich keine Metrik. Die Spurbildung erfordert eine Metrik, aber diese muß nicht verträglich mit benötigt offensichtlich keine Metrik. Die Spurbildung erfordert eine Metrik, aber diese muß nicht verträglich mit  sein. sein.
Der Zusammenhang zwischen  und und  erfordert natürlich speziellere Eigenschaften von erfordert natürlich speziellere Eigenschaften von  . Das ist klar. . Das ist klar. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 20. Dez 2020 10:14 Titel: index_razor Verfasst am: 20. Dez 2020 10:14 Titel: |
 |
|
| Zitat: |
| TomS hat Folgendes geschrieben: |
(4) Laplace-Beltrami
 )
 \qquad (4b) )
wobei (b) mittels Produktregel und Metrik-Kompatibilität folgt
|
Wieso soll das folgen? (4a) ist doch nur eine Schreibweise für die Spur des Tensors  . (Offensichtlich bezeichnest du jetzt diese Spur bereits als " . (Offensichtlich bezeichnest du jetzt diese Spur bereits als " " was die nächste Mehrdeutigkeit einführt. Oder war das ein Versehen?) " was die nächste Mehrdeutigkeit einführt. Oder war das ein Versehen?) |
P.S.: Genau betrachtet ist (4a) wieder ein Beispiel für die mehrdeutige Notation, die ich die ganze Zeit kritisiere. Aus deiner Schreibweise wird nicht mal deutlich ob du tatsächlich  meinst oder meinst oder ) . .
Der letzte Schritt sieht so aus, als hättest du einfach  eingesetzt, was nur funktioniert, wenn du eingesetzt, was nur funktioniert, wenn du ) berechnest. Aber das ist falsch. Das berechnest. Aber das ist falsch. Das 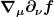 auf der rechten Seite, darf nicht einfach als kovariante Ableitung der Funktion auf der rechten Seite, darf nicht einfach als kovariante Ableitung der Funktion  verstanden werden, sondern als die kovariante Ableitung des Kovektors verstanden werden, sondern als die kovariante Ableitung des Kovektors  . Aber dann funktioniert der Schritt davor nicht. . Aber dann funktioniert der Schritt davor nicht.
Die zweite kovariante Ableitung ist nicht einfach die kovariante Ableitung der kovarianten Ableitung, wie aus der Formel
 = \nabla_Y(\nabla_X f) - \nabla_{\nabla_Y X} f)
ja eigentlich sofort deutlich wird. In deiner Rechnung stecken deshalb m.E. zwei Fehler, die sich gegenseitig aufheben. Das liegt allein an der mehrdeutigen Schreibweise. Ich glaube nicht, daß ich es komplizierter mache als nötig, wenn ich darauf hinweise, daß man sich vor der Rechnung klar machen muß, was die Symbole bedeuten. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18062
|
 TomS Verfasst am: 20. Dez 2020 11:56 Titel: TomS Verfasst am: 20. Dez 2020 11:56 Titel: |
 |
|
| index_razor hat Folgendes geschrieben: | Schreibe hierfür doch mal, so wie es korrekt wäre, ^{\mu\nu} = 0) ... ... |
Denk dir die Klammern bitte dazu.
Die ausgeschriebene Definition steht in (2c). Aufgrund von (1b,c) sollte klar sein, wovon ich rede. Damit wird wahrscheinlich auch der ganze Rest hinfällig.
Es mag sein, dass die Notation sloppy ist, sie ist aber auch fapp; Carroll schreibt das so, Blaul schreibt das so ...
| Zitat: | | Wieso soll das folgen? ... Wieso du die unter die Ableitung ziehen willst, geschweige denn ziehen kannst, hast du immer noch nicht erklärt. |

)
Und jetzt wieder von links die kovariante Ableitung.
Ich ziehe nichts unter die kovariante Ableitung, ich entscheide nur, wo ich die Metrik zum Hoch- bzw. Runterziehen der Indizes hinschreibe.
| Zitat: | Der Tensor  benötigt offensichtlich keine Metrik. benötigt offensichtlich keine Metrik. |
Da wir die ganze Zeit über eine Metrik-kompatible kovariante Ableitung reden, benötigt dieser Tensor natürlich eine Metrik; sie steckt in der Definition des Levi-Cevita-Zusammenhangs.
Der ganze Witz besteht darin z.z., dass linke und rechte Seite von (6) übereinstimmen. Der Beweis benötigt zwingend eine Metrik: links, weil sonst die Definition nicht funktioniert; rechts für die Rechnung, weil die nur mit (1,2) funktioniert - zumindest lese ich das in allen Quellen.
| index_razor hat Folgendes geschrieben: | Der letzte Schritt sieht so aus, als hättest du einfach  eingesetzt ... eingesetzt ... |
Ja, ich kenne keine andere Definition des Levi-Cevita-Zusammenhangs auf eine skalare Funktion.
| index_razor hat Folgendes geschrieben: | | In deiner Rechnung stecken deshalb m.E. zwei Fehler, die sich gegenseitig aufheben. |
Nein, ich denke lediglich, dass die Notation genau das ausdrückt, was fapp erlaubt ist.
| index_razor hat Folgendes geschrieben: | | Ich glaube nicht, daß ich es komplizierter mache als nötig, wenn ich darauf hinweise, daß man sich vor der Rechnung klar machen muß, was die Symbole bedeuten. |
Das ist schon ok.
Es wäre jedoch schön, wenn aus deiner Überlegung außerdem folgen würde, was man nachrechnen und an diversen Stellen nachlesen kann. So bleibt bei mir hängen, dass die Tangentialraum-Notation zwar mathematisch präzise ist, jedoch nichts dazu beitragen kann, was viele Physiker hendsärmelig anwenden - das wird ja nicht falsch sein.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 20. Dez 2020 14:28 Titel: index_razor Verfasst am: 20. Dez 2020 14:28 Titel: |
 |
|
| TomS hat Folgendes geschrieben: | | index_razor hat Folgendes geschrieben: | Schreibe hierfür doch mal, so wie es korrekt wäre, ^{\mu\nu} = 0) ... ... |
Denk dir die Klammern bitte dazu.
Die ausgeschriebene Definition steht in (2c). Aufgrund von (1b,c) sollte klar sein, wovon ich rede. Damit wird wahrscheinlich auch der ganze Rest hinfällig.
|
Das Problem ist doch nicht, daß ich mir keine Klammern dazudenken will.
Für mich ergibt deine Rechnung (4a) und (4b) nach wie vor keinen Sinn; insbesondere der behauptete Zusammenhang zur Metrikverträglichkeit. An keiner Stelle kommt dort irgendwo die Ableitung  , also auch keine ihrer Komponenten , also auch keine ihrer Komponenten ^{\mu\nu}) , vor. Also spielt auch keine Rolle, daß sie alle verschwinden. , vor. Also spielt auch keine Rolle, daß sie alle verschwinden.
| Zitat: |
Es mag sein, dass die Notation sloppy ist, sie ist aber auch fapp; Carroll schreibt das so, Blaul schreibt das so ... |
Es geht nicht nur um die Notation in (2a-c). Ich weiß, wie ich diese Gleichung zu lesen habe. Es geht um deine Rechnung (4a), (4b).
| Zitat: |
Ich ziehe nichts unter die kovariante Ableitung, ich entscheide nur, wo ich die Metrik zum Hoch- bzw. Runterziehen der Indizes hinschreibe.
|
Corbi aber. Zumindest war seine Frage, ob etwas dergleichen erlaubt ist.
Ansonsten hat das ganze auch nichts mit (2a-c) zu tun.
| Zitat: |
| Zitat: | Der Tensor  benötigt offensichtlich keine Metrik. benötigt offensichtlich keine Metrik. |
Da wir die ganze Zeit über eine Metrik-kompatible kovariante Ableitung reden, benötigt dieser Tensor natürlich eine Metrik; sie steckt in der Definition des Levi-Cevita-Zusammenhangs.
|
Ich weiß, daß wir von einem metrikverträglichen Zusammenhang reden. Das ist doch nicht der Punkt. Einfach eine Menge zutreffender Aussagen über 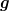 und und  zusammenzurühren, ergibt noch kein korrektes Argument. Ich hoffe die logische Kohärenz deiner Aussagen spielt dabei auch irgendeine Rolle für dich. zusammenzurühren, ergibt noch kein korrektes Argument. Ich hoffe die logische Kohärenz deiner Aussagen spielt dabei auch irgendeine Rolle für dich.
Die Definition von  benötigt keine Metrik. Auch nicht benötigt keine Metrik. Auch nicht
_{ij} = \partial_i\partial_j f - \Gamma_{ij}^k \partial_k f)
mit  . .
Beides funktioniert für beliebige affine Zusammenhänge. Lediglich die anschließende Spurbildung benötigt eine Metrik. Sind wir uns zumindest bis hierhin einig?
| Zitat: |
Der ganze Witz besteht darin z.z., dass linke und rechte Seite von (6) übereinstimmen. Der Beweis benötigt zwingend eine Metrik: links, weil sonst die Definition nicht funktioniert; rechts für die Rechnung, weil die nur mit (1,2) funktioniert - zumindest lese ich das in allen Quellen.
|
Wieso ist das "der ganze Witz"? Die linke Seite ist einfach eine Konsequenz aus  . Dies benötigt natürlich eine Metrik für die Definition von . Dies benötigt natürlich eine Metrik für die Definition von  , allerdings überhaupt keinen affinen Zusammenhang, geschweige denn einen metrikverträglichen. , allerdings überhaupt keinen affinen Zusammenhang, geschweige denn einen metrikverträglichen.
Natürlich ist es, gerade aus diesem Grund, interessant zu wissen, warum und unter welchen Bedingungen

Wenn ich mich richtig erinnere, spielt hier aber nur die Torsionsfreiheit eine Rolle, nicht  . Aber da kann ich mich auch irren. . Aber da kann ich mich auch irren.
Ich habe allerdings Corbis Frage auch nicht so verstanden, daß es um diese Gleichheit geht. Er verwendet in beiden Formeln immer die kovariante Ableitung. Deswegen glaube ich, seine Frage läuft nur darauf hinaus, welchen der beiden Indizes in 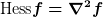 man heben muß, um die Spur zu bilden. Daß man hierzu irgendwelche Ableitungen von man heben muß, um die Spur zu bilden. Daß man hierzu irgendwelche Ableitungen von 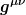 berücksichtigen muß, ist m.E. ein Trugschluß. berücksichtigen muß, ist m.E. ein Trugschluß.
| Zitat: |
| index_razor hat Folgendes geschrieben: | Der letzte Schritt sieht so aus, als hättest du einfach  eingesetzt ... eingesetzt ... |
Ja, ich kenne keine andere Definition des Levi-Cevita-Zusammenhangs auf eine skalare Funktion.
|
Ich auch nicht. Dann bedeutet aber ) und das heißt, deine Berechnung des Laplace-Operators von f in (4a) ist falsch. Dort muß stehen und das heißt, deine Berechnung des Laplace-Operators von f in (4a) ist falsch. Dort muß stehen ) und erst in diesem Tensor darf man die Indizes kontrahieren, nicht vorher. Es wird also nirgendwo die kovariante Ableitung von f nach und erst in diesem Tensor darf man die Indizes kontrahieren, nicht vorher. Es wird also nirgendwo die kovariante Ableitung von f nach  berechnet, sondern nur das kovariante Differential von berechnet, sondern nur das kovariante Differential von  und anschließend kontrahiert. Bist du nicht der Meinung, daß es wichtig ist, auf diesen Unterschied hinzuweisen? und anschließend kontrahiert. Bist du nicht der Meinung, daß es wichtig ist, auf diesen Unterschied hinzuweisen?
| Zitat: |
| index_razor hat Folgendes geschrieben: | | Ich glaube nicht, daß ich es komplizierter mache als nötig, wenn ich darauf hinweise, daß man sich vor der Rechnung klar machen muß, was die Symbole bedeuten. |
Das ist schon ok.
Es wäre jedoch schön, wenn aus deiner Überlegung außerdem folgen würde, was man nachrechnen und an diversen Stellen nachlesen kann. So bleibt bei mir hängen, dass die Tangentialraum-Notation zwar mathematisch präzise ist, jedoch nichts dazu beitragen kann, was viele Physiker hendsärmelig anwenden - das wird ja nicht falsch sein. |
Ich möchte in erster Linie klären, was real hinter dem ganzen Indexschlamassel steckt. Ich halte es für schlecht, wenn die Notation Scheinprobleme erzeugt, die man mit echten mathematischen Problemen verwechselt. Ich war nicht sicher um welche davon es sich in der Originalfrage dreht.
Meine Notation für diesen Zweck stammt übrigens fast wörtlich aus dem ersten Wikipediaartikel, den du verlinkt hast. Wenn du bezweifelst, daß sie zur Klärung beitragen kann, warum verlinkst du dann den Artikel?
Ich kann mich auch nicht erinnern eine Rechnung wie deine (4a) schon mal irgendwo anders gesehen zu haben. Deswegen frage ich dich was sie bedeutet. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18062
|
 TomS Verfasst am: 20. Dez 2020 16:17 Titel: TomS Verfasst am: 20. Dez 2020 16:17 Titel: |
 |
|
Metrik und Metrikverträglichkeit sind deswegen wichtig, weil wir über den Levi-Cevita-Zusammenhang (und dessen Metrikverträglichkeit) reden, weil der spezielle Laplace-Beltrami-Operator ausschließlich für den Cevita-Zusammenhang definiert ist und weil der Zusammenhang der beiden Formen nur unter dieser Bedingung gilt; ich lese jedenfalls alle mir zur Verfügung stehenden Quellen so.
Außerdem hat Corbi diesbzgl. explizit eine Frage gestellt. Mein Hinweis auf die spezielle Form des Laplace-Beltrami-Operators war wahrscheinlich kontraproduktiv, da der Laplace-Beltrami-Operators zunächst anders definiert werden kann.
Zu (4)
 ist zunächst nur ein Symbol, das zu definieren ist: ist zunächst nur ein Symbol, das zu definieren ist:
}{=} \nabla_\mu (\nabla^\mu f ))
}{=} g_{\mu\nu} (\nabla^\nu (\nabla^\mu f ) ))
}{=} \nabla_\mu (g^{\mu\nu}(\nabla_\nu f ) ) )
(a) entspricht der Anwendung der kovarianten Ableitung auf einen Vektor, der mittels der kovarianten Ableitung eines Skalars gewonnen wurde. Die Kontraktion wird letztlich durch (b) definiert. In (c) ziehe ich - ausgehend von (a) - lediglich den Index einen Vektors - der mittels der kovarianten Ableitung eines Skalars gewonnen wurde - hoch.
Nach meinen Verständnis und Rechnungen sind alle diese Definitionen identisch - vorgausgesetzt man verwendet speziell den metrik-kompatiblen Levi-Cevita Zusammenhang.
Zu (5,6)
 )
Diese Gleichung folgt aus den o.g. (b, c) unter Verwendung der Eigenschaften der Metrik und des metrik-kompatiblen Levi-Cevita Zusammenhangs.
Natürlich muss man die Äquivalenz zeigen, aber dass das funktioniert, habe ich in (6) erledigt. Für mich ist damit eigtl. alles klar.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 20. Dez 2020 17:20 Titel: index_razor Verfasst am: 20. Dez 2020 17:20 Titel: |
 |
|
| TomS hat Folgendes geschrieben: | Metrik und Metrikverträglichkeit sind deswegen wichtig, weil wir über den Levi-Cevita-Zusammenhang (und dessen Metrikverträglichkeit) reden, weil der spezielle Laplace-Beltrami-Operator ausschließlich für den Cevita-Zusammenhang definiert ist
|
Was ist der "spezielle Laplace-Beltrami-Operator"? Ich bezog mich auf die Definition aus einer deiner Quellen, ) . Diese Definition funktioniert für beliebige affine Zusammenhänge. Stimmen wir darin überein? . Diese Definition funktioniert für beliebige affine Zusammenhänge. Stimmen wir darin überein?
| Zitat: |
und weil der Zusammenhang der beiden Formen nur unter dieser Bedingung gilt; ich lese jedenfalls alle mir zur Verfügung stehenden Quellen so.
|
Klar, der Zusammenhang ) gilt nicht für jedes gilt nicht für jedes  . Das sagte ich ja bereits. Kann auch sein, daß man dafür . Das sagte ich ja bereits. Kann auch sein, daß man dafür  benötigt. benötigt.
| Zitat: |
Außerdem hat Corbi diesbzgl. explizit eine Frage gestellt. Mein Hinweis auf die spezielle Form des Laplace-Beltrami-Operators war wahrscheinlich kontraproduktiv, da der Laplace-Beltrami-Operators zunächst anders definiert werden kann.
|
Ich fand das nicht kontraproduktiv. Beide Definitionen finde ich wichtig, auch ihren Zusammenhang. Das interessante ist doch gerade, daß sie mit völlig unterschiedlichen Voraussetzungen arbeiten:  mit Metrik, aber ohne jeglichen Zusammenhang, mit Metrik, aber ohne jeglichen Zusammenhang,  mit Metrik und irgendeinem Zusammenhang. Die Gleichheit gilt unter bestimmten Bedingungen an mit Metrik und irgendeinem Zusammenhang. Die Gleichheit gilt unter bestimmten Bedingungen an  . Ich habe dies lediglich nicht als den Hintergrund von Corbis Frage gesehen. Ich glaube er hat . Ich habe dies lediglich nicht als den Hintergrund von Corbis Frage gesehen. Ich glaube er hat  , also auch deine linke Seite von (6) gar nicht verwendet. , also auch deine linke Seite von (6) gar nicht verwendet.
| Zitat: |
Zu (4)
 ist zunächst nur ein Symbol, das zu definieren ist: ist zunächst nur ein Symbol, das zu definieren ist:
}{=} \nabla_\mu (\nabla^\mu f ))
}{=} g_{\mu\nu} (\nabla^\nu (\nabla^\mu f ) ))
}{=} \nabla_\mu (g^{\mu\nu}(\nabla_\nu f ) ) )
(a) entspricht der Anwendung der kovarianten Ableitung auf einen Vektor, der mittels der kovarianten Ableitung eines Skalars gewonnen wurde. |
Ja, die Beschreibung klingt nach der kovarianten Ableitung des Kovektors  . Das Problem ist nur, daß das ganze nichts mit der Eigenschaft . Das Problem ist nur, daß das ganze nichts mit der Eigenschaft  zu tun hat. Du mußt erst zu tun hat. Du mußt erst (\cdot , e_\mu)) bilden. Dann mit dem verbleibenden Index kontrahieren. Andernfalls ist die Rechnung falsch. Hier spielt doch gerade der Unterschied zwischen bilden. Dann mit dem verbleibenden Index kontrahieren. Andernfalls ist die Rechnung falsch. Hier spielt doch gerade der Unterschied zwischen =\nabla_\mu(\partial_\nu f)) und und _{\mu\nu} = (\nabla \dd f)_{\mu\nu}) die entscheidende Rolle. die entscheidende Rolle.
| Zitat: |
Die Kontraktion wird letztlich durch (b) definiert.
|
Natürlicher wäre zwar ) , aber ich sehe beides als äquivalent per Definition von , aber ich sehe beides als äquivalent per Definition von  . .
Auch hier gilt wieder dasselbe: In dieser Gleichung (b) darf man ) nicht so interpretieren, daß erst die kovariante Ableitung nicht so interpretieren, daß erst die kovariante Ableitung
)
berechnet wird, dann auf das Ergebnis, welches eine Funktion ist, nochmal die Ableitung  angewendet und zum Schluß kontrahiert wird. angewendet und zum Schluß kontrahiert wird.
Das kann nicht gemeint sein. Aber nicht nur deine Notation, inklusive Klammerung, drängt diese Interpretation förmlich auf. Auch dein Argument mit der Voraussetzung  legt nahe, daß du denkst, es würde genau dies passieren. Wenn du es so meinst und das nicht nur eine laxe Schreibweise für etwas anderes ist, dann wäre das Argument falsch. legt nahe, daß du denkst, es würde genau dies passieren. Wenn du es so meinst und das nicht nur eine laxe Schreibweise für etwas anderes ist, dann wäre das Argument falsch.
| Zitat: |
In (c) ziehe ich - ausgehend von (a) - lediglich den Index einen Vektors - der mittels der kovarianten Ableitung eines Skalars gewonnen wurde - hoch.
Nach meinen Verständnis und Rechnungen sind alle diese Definitionen identisch - vorgausgesetzt man verwendet speziell den metrik-kompatiblen Levi-Cevita Zusammenhang.
|
Und ich denke hier irrst du dich. Alle Rechnungen basieren lediglich auf (siehe die Definition aus deinem Wikipedia-Link)
 - \nabla_{\nabla_Y X}f \qquad\text{(1)})
Dies ist für beliebiges  ein kovarianter Tensor zweiter Stufe. Aus diesem Grund allein kann man ihn mit Hilfe einer beliebigen Metrik zu einem Skalar kontrahieren. Das sieht so aus ein kovarianter Tensor zweiter Stufe. Aus diesem Grund allein kann man ihn mit Hilfe einer beliebigen Metrik zu einem Skalar kontrahieren. Das sieht so aus
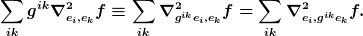
Alle diese Gleichungen gelten allein wegen des Tensorcharakters von (1). Man benötigt also lediglich die Homogenitätseigenschaften
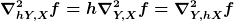
für beliebige Funktionen h. Das hat noch nichts mit der Metrikverträglichkeit zu tun.
| Zitat: |
Zu (5,6)
 )
Diese Gleichung folgt aus den o.g. (b, c) unter Verwendung der Eigenschaften der Metrik und des metrik-kompatiblen Levi-Cevita Zusammenhangs.
Natürlich muss man die Äquivalenz zeigen, aber dass das funktioniert, habe ich in (6) erledigt. Für mich ist damit eigtl. alles klar. |
Das mag zwar richtig sein. Ich hatte aber den Hintergrund von Corbis Frage anders verstanden. Von der rechten Seite hat er nie was geschrieben. Die stammt ja lediglich aus deinem ersten Beitrag. Ich ging davon aus, daß er die Eigenschaften der Definition

diskutieren möchte. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18062
|
 TomS Verfasst am: 22. Dez 2020 10:50 Titel: TomS Verfasst am: 22. Dez 2020 10:50 Titel: |
 |
|
Mein Problem ist, dass ich so langsam nicht mehr verstehe, was du mir eigentlich erklären willst. Dass die Indexnotation der Physiker sloppy ist? Das weiß ich. Und wir – ich zusammen mit vielen anderen – sind uns bewusst, was das bedeutet. Siehe z.B. auch hier: https://en.m.wikipedia.org/wiki/List_of_formulas_in_Riemannian_geometry
https://en.m.wikipedia.org/wiki/Christoffel_symbols
Komponenten der kovarianten Ableitung einer skalaren Funktion – sloppy
_\mu = \nabla_\mu f = \partial_\mu f )
Das selbe für einen Vektor – der später speziell einem Gradienten entspricht – sloppy

_\mu = \partial_\nu V_\mu - \Gamma^\rho_{\mu\nu} V_\rho = \left( \partial_\nu \delta^\rho_\mu - \Gamma^\rho_{\mu\nu} \right) V_\rho )
Der Laplace-Beltrami-Operator ist letztlich die Verallgemeinerung – sloppy
 )
Letzteres entspricht gerade
 \partial_\rho f )
Die Metrik-Verträglichkeit besagt, dass

Diese Gleichungen verwende ich, um die Äquivalenz – Notation sloppy
 = g^{\mu\nu} ( \nabla_\mu ( \partial_\nu f ) ) )
zu zeigen; die Rechnung ist etwas länger, nicht schwer – und nicht sloppy.
Die Metrik-Veträglichkeit benötigt man nicht, um irgendwo direkt die kovariante Ableitung einer Metrik berechnen, jedoch im Zuge der Rechnung für die Identität

Also nochmal, da ist nichts falsch.
Dann: Klar kann man Laplace-Operatoren auch für andere Zusammenhänge definieren. Mit „speziellem Laplace-Beltrami-Operator“ meine ich, dass ich für diesen nie eine andere Definition als mittels Levi-Cevita-Zusammenhang gesehen habe, d.h. implizit immer für eine Metrik. Für andere affine Zusammenhänge habe ich das nicht betrachtet.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago.
Zuletzt bearbeitet von TomS am 22. Dez 2020 14:22, insgesamt 2-mal bearbeitet |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18062
|
 TomS Verfasst am: 22. Dez 2020 11:32 Titel: TomS Verfasst am: 22. Dez 2020 11:32 Titel: |
 |
|
Doch, jetzt ist klar, was nicht passt; (c) ist nicht sloppy sondern Quatsch. Sorry, ich stand wirklich auf der Leitung.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Corbi
Anmeldungsdatum: 17.07.2018
Beiträge: 296
|
 Corbi Verfasst am: 26. Dez 2020 18:16 Titel: Corbi Verfasst am: 26. Dez 2020 18:16 Titel: |
 |
|
Vielen Dank euch beiden, dass ihr euch mit meiner Frage so lange auseinandergesetzt habt. Ich habe mir eure Diskussion durchgelesen und versucht zu verstehen, bin aber eher noch mehr verwirrt.
Mir war tatsächlich nicht bewusst, dass die Schreibweise:
 nicht ganz eindeutig ist. nicht ganz eindeutig ist.
Bisher habe ich es aber so gelernt, dass man die kovariante Konstanz des metrischen Tensors so:  notiert. notiert.
Ich habe verstanden, dass diese Notation gewissermaßen problemhaft ist, da  als Skalarprodukt natürlich auch ein Skalar darstellt, dass partiell abgeleitet werden muss. als Skalarprodukt natürlich auch ein Skalar darstellt, dass partiell abgeleitet werden muss.
Eine Diskussion zu diesem Thema( das Vektor- und Tensorkomponenten ja eigentlich immer Skalarprodukt sind) hatte ich schon vor ca. einem halben mit index_razor wo es um Kugelwellenlösungen der homogenen Wellengleichung in einer flachen Raumzeit ging.
Wenn ich das jetzt richtig verstehe müsste man um konsistent zu bleiben Kovariante Ableitungen (vom Vektor A z.B.) eigentlich immer so ^{\nu}) notieren. notieren.
Bisher bin ich bei meinen Kenntnissen zur Differentialgeometrie aber nur mit Index-Notation vertraut, daher fällt es mir schwer index_razors Beiträge nachzuvollziehen. Ich denke auf die schnelle kann ich mir ein Verständnis für die Koordinatenunabhängigen Darstellungen auch nicht aneignen. Auch das Thema mit den partiellen Ableitungen als Basisvektoren des Tangentialraums leuchtet mir noch nicht so ganz ein.
Wenn einer von euch Lust hat, kann er ja nochmal versuchen den gesamten Sachverhalt um die ursprüngliche Frage kurz und knapp darzustellen, sodass ich zumindest eine klare Übersicht habe, was jetzt korrekt und welche Notation an welche Stelle konsistent ist. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 29. Dez 2020 19:14 Titel: index_razor Verfasst am: 29. Dez 2020 19:14 Titel: |
 |
|
| Corbi hat Folgendes geschrieben: |
Mir war tatsächlich nicht bewusst, dass die Schreibweise:
 nicht ganz eindeutig ist. nicht ganz eindeutig ist.
Bisher habe ich es aber so gelernt, dass man die kovariante Konstanz des metrischen Tensors so:  notiert. notiert.
Ich habe verstanden, dass diese Notation gewissermaßen problemhaft ist, da  als Skalarprodukt natürlich auch ein Skalar darstellt, dass partiell abgeleitet werden muss. als Skalarprodukt natürlich auch ein Skalar darstellt, dass partiell abgeleitet werden muss.
|
Ja, das ist im Prinzip die Ursache für die Mehrdeutigkeit. In der Physikliteratur wird die Schreibweise  oft für den Tensor, also die multilineare Abbildung oft für den Tensor, also die multilineare Abbildung  = e_\mu\cdot e_\nu) verwendet. Das nennt sich abstrakte Indexnotation, d.h. die Indizes bezeichnen nicht die Komponenten des Tensors, sondern zeigen lediglich an, an welcher Stelle Vektoren bzw. Kovektoren erwartet werden. Der Vorteil dieser Notation ist m.E. hauptsächlich, daß man beliebige Kontraktionen sowie den Übergang von Vektoren zu Kovektoren und umgekehrt leicht hinschreiben kann. Die entsprechenden Formeln sehen identisch aus zu den Formeln im Ricci-Kalkül, wenn man die Tensoren mit ihren Komponenten bzgl. einer fixen Basis (und zugehöriger Dualbasis) identifiziert. verwendet. Das nennt sich abstrakte Indexnotation, d.h. die Indizes bezeichnen nicht die Komponenten des Tensors, sondern zeigen lediglich an, an welcher Stelle Vektoren bzw. Kovektoren erwartet werden. Der Vorteil dieser Notation ist m.E. hauptsächlich, daß man beliebige Kontraktionen sowie den Übergang von Vektoren zu Kovektoren und umgekehrt leicht hinschreiben kann. Die entsprechenden Formeln sehen identisch aus zu den Formeln im Ricci-Kalkül, wenn man die Tensoren mit ihren Komponenten bzgl. einer fixen Basis (und zugehöriger Dualbasis) identifiziert.
Durch die Interpretation der Formeln in abstrakter Indexnotation verschwindet die Mehrdeutigkeit, denn Funktionen besitzen niemals irgendwelche Indizes (oder wenn man sie benötigen sollte, z.B. für Tensorkomponenten, haben sie typischerweise Indizes aus einem anderen Alphabet), und deshalb bedeutet 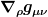 immer die kovariante Ableitung eines Tensors, nicht seiner Komponentenfunktion. immer die kovariante Ableitung eines Tensors, nicht seiner Komponentenfunktion.
| Zitat: |
Wenn ich das jetzt richtig verstehe müsste man um konsistent zu bleiben Kovariante Ableitungen (vom Vektor A z.B.) eigentlich immer so ^{\nu}) notieren. notieren.
|
Das kommt darauf an. In erster Linie sollten Autoren genau definieren, was 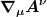 bedeutet bevor sie diese Schreibweise verwenden. bedeutet bevor sie diese Schreibweise verwenden.
Wald z.B. schreibt für die kovariante Ableitung eines Vektors ebenfalls  . Die einzelnen Terme haben hier eine ganz präzise Bedeutung im abstrakten Indexkalkül, den er vorher einführt. Die linke Seite ist der (1,1)-Tensor . Die einzelnen Terme haben hier eine ganz präzise Bedeutung im abstrakten Indexkalkül, den er vorher einführt. Die linke Seite ist der (1,1)-Tensor
 \mapsto \langle \omega, \nabla_X v\rangle= \omega(\nabla_X v).)
Die Größe  ist hier übrigens ein Tensor der Stufe (1, 2). (Dessen einziges "Manko" ist, daß seiner Definition eine Karte zugrundeliegt, bzgl. deren ist hier übrigens ein Tensor der Stufe (1, 2). (Dessen einziges "Manko" ist, daß seiner Definition eine Karte zugrundeliegt, bzgl. deren  definiert ist, was aber seiner Tensorhaftigkeit keinen Abbruch tut.) definiert ist, was aber seiner Tensorhaftigkeit keinen Abbruch tut.)
Wenn Bücher/Skripte einfach  verwenden ohne klarzustellen ob sie sich lediglich im abstrakten Indexkalkül ausdrücken oder stattdessen von der kovarianten Ableitung einer Tensorkomponente reden, hantieren sie einfach mit sinnlosen Formelzeichen. Dann muß man versuchen aus dem Kontext schlau zu werden (was oft möglich ist) oder sich nach besserer Literatur umsehen. verwenden ohne klarzustellen ob sie sich lediglich im abstrakten Indexkalkül ausdrücken oder stattdessen von der kovarianten Ableitung einer Tensorkomponente reden, hantieren sie einfach mit sinnlosen Formelzeichen. Dann muß man versuchen aus dem Kontext schlau zu werden (was oft möglich ist) oder sich nach besserer Literatur umsehen.
| Zitat: |
Wenn einer von euch Lust hat, kann er ja nochmal versuchen den gesamten Sachverhalt um die ursprüngliche Frage kurz und knapp darzustellen, sodass ich zumindest eine klare Übersicht habe, was jetzt korrekt und welche Notation an welche Stelle konsistent ist. |
Zunächst schadet es wohl nicht, sich noch einmal in Ruhe klar zu machen, welche Größe wir hier eigentlich ausrechnen wollen. Der d'Alembert-Operator oder Laplace-Operator oder wie auch immer man ihn nennt, soll eine Verallgemeinerung von =\text{div grad}f) sein. (Hier ist zunächst mal sein. (Hier ist zunächst mal  der Nabla-Operator der klassischen Vektoranalysis, nicht die kovariante Ableitung.) der Nabla-Operator der klassischen Vektoranalysis, nicht die kovariante Ableitung.)
Wir suchen also eine Operation, die eine Funktion höchstens zweimal ableitet und wieder ein Funktion ergibt. Die natürliche Definition der ersten Ableitung einer Funktion ist das Differential  . Dies ist ein Kovektor im Gegensatz zum Gradienten, der ein Vektor ist. Andererseits benötigt . Dies ist ein Kovektor im Gegensatz zum Gradienten, der ein Vektor ist. Andererseits benötigt  weder eine Metrik noch eine kovariante Ableitung. Wollen wir aber einen Vektor aus weder eine Metrik noch eine kovariante Ableitung. Wollen wir aber einen Vektor aus  konstruieren, benötigen wir eine Metrik g. Der Gradient von f ist nämlich der eindeutige Vektor definiert über die Beziehung konstruieren, benötigen wir eine Metrik g. Der Gradient von f ist nämlich der eindeutige Vektor definiert über die Beziehung
 = g(\text{grad}f, v))
für alle v.
Als nächstes wäre also zu klären, was die Analogie zur Divergenz eines Vektorfeldes ist. Diese Frage verschiebe ich mal nach ganz hinten. Stattdessen wende ich mich zunächst mal ganz allgemein den Eigenschaften des kovarianten Differentials von 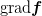 zu. Deine erste Gleichung sieht nämlich genauso wie diese Größe aus, von der anschließend die Spur gebildet wird, d.h. ich behaupte in deiner ersten Gl. geht es um die Größe zu. Deine erste Gleichung sieht nämlich genauso wie diese Größe aus, von der anschließend die Spur gebildet wird, d.h. ich behaupte in deiner ersten Gl. geht es um die Größe
)
oder
^a)
in (leicht modifizierter) abstrakter Indexnotation, worin ^a) zu verstehen ist. Diese Zusammenhänge sollten m.E. klar sein. Falls nicht, denke ich, wir sollten es klären. zu verstehen ist. Diese Zusammenhänge sollten m.E. klar sein. Falls nicht, denke ich, wir sollten es klären.
Ignorieren wir im Augenblick mal die explizite Berechnung von  . Es gibt nämlich noch eine andere Herangehensweise: wir bleiben bei . Es gibt nämlich noch eine andere Herangehensweise: wir bleiben bei  , bilden die kovariante Ableitung dieses Kovektors und anschließend davon die Spur. Die Ableitung eines Kovektors ergibt wieder einen Kovektor , bilden die kovariante Ableitung dieses Kovektors und anschließend davon die Spur. Die Ableitung eines Kovektors ergibt wieder einen Kovektor 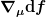 und kann auf einen beliebigen Vektor v angewendet werden und kann auf einen beliebigen Vektor v angewendet werden (v)) . Die Spur ist dann . Die Spur ist dann
 (e_\mu))
Hier interpretiere ich also 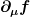 als den Kovektor als den Kovektor  in abstrakter Indexnotation. (Besser wäre eigentlich die Schreibweise in abstrakter Indexnotation. (Besser wäre eigentlich die Schreibweise _a) , weil die Definition von , weil die Definition von  unabhängig von der Karte ist.) Das Hochstellen des Index in unabhängig von der Karte ist.) Das Hochstellen des Index in  ist noch ein kleines Mysterium. Normalerweise bedeutet ist noch ein kleines Mysterium. Normalerweise bedeutet  die Ableitung nach dem Basisvektor die Ableitung nach dem Basisvektor  . Die Ableitung nach einem Kovektor ist nicht definiert. Ich interpretiere also . Die Ableitung nach einem Kovektor ist nicht definiert. Ich interpretiere also  analog zu analog zu  , d.h. als , d.h. als 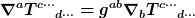 im abstrakten Indexkalkül. D.h. im abstrakten Indexkalkül. D.h.  ist der Vektor, für den gilt ist der Vektor, für den gilt
 = \nabla_\mu\dd f (v))
für alle v. (Das ist derselbe Zusammenhang wie in der Definition von 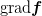 .) .)
Mit dieser Interpretation haben wir, denke ich, deine Frage folgendermaßen umformuliert: Gilt
 (e_\mu) = \sum_\mu g(\nabla_\mu \text{grad}f, e_\mu)?)
Antwort: ja, wenn die Ableitung metrikverträglich (isometrisch) ist, also  . Das kann man leicht nachrechnen, wenn man einige einfache Rechenregeln der kovarianten Ableitung berücksichtigt. . Das kann man leicht nachrechnen, wenn man einige einfache Rechenregeln der kovarianten Ableitung berücksichtigt.
Es gilt
(Y) = \nabla_X(\dd f(X)) -\dd f(\nabla_X Y).)
(Dies folgt aus der Produktregel  =\nabla_X A \otimes B + A\otimes\nabla_X B) und der Vertauschbarkeit der Ableitung mit Kontraktionen.) und der Vertauschbarkeit der Ableitung mit Kontraktionen.)
Also mit der Definition von 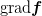 : :
(Y) = \nabla_X(g(\text{grad}f, X)) - g(\text{grad} f, \nabla_X Y).)
Metrikverträglichkeit impliziert ) = g(\nabla_XZ,Y)+g(Z,\nabla_XY)) . Setzt man ein ergibt sich . Setzt man ein ergibt sich
(Y) = g(\nabla_X\text{grad}f, Y).)
Spurbildung ( und Summation über und Summation über  ) ergibt die behauptete Gleichheit. ) ergibt die behauptete Gleichheit.
Zusatz
Formal ist damit erstmal die Gleichheit von  aus den präzisen Definitionen der beteiligten Größen sowie aus der Metrikverträglichkeit von aus den präzisen Definitionen der beteiligten Größen sowie aus der Metrikverträglichkeit von  abgleitet. abgleitet.
Jetzt komme ich nochmal auf die Frage zurück was  eigentlich mit der Divergenz von eigentlich mit der Divergenz von 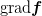 , und damit mit dem Laplace-Operator , und damit mit dem Laplace-Operator  zu tun hat. Die kovariante Ableitung ist zwar eine Möglichkeit die "zweite Ableitung von f" zu definieren. Aber es ist nicht diejenige, die man normalerweise zur Definition von zu tun hat. Die kovariante Ableitung ist zwar eine Möglichkeit die "zweite Ableitung von f" zu definieren. Aber es ist nicht diejenige, die man normalerweise zur Definition von 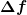 für Funktionen verwenden würde. für Funktionen verwenden würde.
Tatsächlich benötigt die Divergenz eines Vektorfeldes überhaupt keine kovariante Ableitung. Sie benötigt lediglich eine Volumenform  . Definiert man für das Vektorfeld X die folgende 3-Form durch . Definiert man für das Vektorfeld X die folgende 3-Form durch
^i X^i \dd x^0\wedge\cdots \widehat{\dd x^i}\cdots \wedge\dd x^3)
(das ^ bedeutet, daß der Term im Produkt fehlt), dann läßt sich hiervon leicht das äußere Differential berechnen:
\text{vol},)
d.h. das Differential von  ergibt wieder ergibt wieder 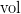 bis auf einen skalaren Faktor. Dieser Faktor ist die Divergenz von X bis auf einen skalaren Faktor. Dieser Faktor ist die Divergenz von X
.)
Wenn wir hier  einsetzen, erhalten wir sofort die schon bekannte Formel einsetzen, erhalten wir sofort die schon bekannte Formel
) . .
Falls das alles nicht ganz nachvollziehbar ist, ist das nicht weiter schlimm. Die wichtige Nachricht ist lediglich, daß die Definition
)
überhaupt keine kovariante Ableitung benötigt, also auch erst recht keinen Levi-Civita-Zusammenhang. Wir benötigen nur eine Metrik (und 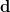 , was wir immer haben). , was wir immer haben).
Wenn wir allerdings einen affinen Zusammenhang  haben und wenn dieser torsionsfrei ist, dann existiert eine einfache Beziehung zwischen haben und wenn dieser torsionsfrei ist, dann existiert eine einfache Beziehung zwischen 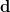 und und  angewandt auf Differentialformen, nämlich angewandt auf Differentialformen, nämlich
(X_0, \ldots, X_n) = \sum_{i}(-1)^i(\nabla_{X_i}\omega)(X_{0}, \ldots, \widehat{X_i},\ldots, X_{n}),)
d.h. wir können  auch mit Hilfe der (torsionsfreien) kovarianten Ableitung von auch mit Hilfe der (torsionsfreien) kovarianten Ableitung von  berechnen. Damit können wir letztlich -- soweit ich das sehe, ich habe aber nicht alle Details nachvollzogen -- einen Zusammenhang zwischen berechnen. Damit können wir letztlich -- soweit ich das sehe, ich habe aber nicht alle Details nachvollzogen -- einen Zusammenhang zwischen
\text{vol} = \dd i_{\text{grad}f}\text{vol}) und und 
herstellen, also letztlich zur Größe 
Zusammenfassung
Wenn ich mich nicht täusche gilt also

Alle drei Gleichheiten gelten damit genau für die Levi-Civita-Zusammenhänge. |
|
 |
Corbi
Anmeldungsdatum: 17.07.2018
Beiträge: 296
|
 Corbi Verfasst am: 02. Jan 2021 18:41 Titel: Corbi Verfasst am: 02. Jan 2021 18:41 Titel: |
 |
|
Ok also die Ursprüngliche Frage ist für mich damit im groben geklärt.
Aber irgendwie verwirrt mich das immernoch mit den Tensorkomponenten als Skalare Funktionen.
In dem ersten Skript, das ich zur Tensoranalysis gelesen habe wird die kovariante Ableitung wie folgt eingeführt:
Seien

die Komponenten eines Vektors bezüglich einer bestimmten Basis, dann ist der Ausdruck

im allgemeinen kein Tensor mehr.
Ein Tensor (z.B. der Stufe (2,0)) wird in diesem Skript dadurch definiert, dass sich seine Komponenten wie folgt transformieren:
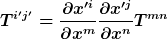
Das Objekt

ist damit kein Tensor, weil:
 )
nach Ausführen der Produktregel die obige Definition nicht erfüllt.
Daher wird dann für die Ableitung der Tensor-/Vektorkomponenten die kovariante Ableitung eingeführt, die dazu da ist den Tensorcharakter bei der Ableitung zu erhalten.
Es wird dann der folgenden Ansatz einer kovarianten Aleitung gemacht:

Die Komponenten von Gamma sind dabei zunächst noch unbestimmt. Es wird nur gefordert, dass  (also dass diese kovariante Ableitung die obige Tensordefinition erfüllt), sowie dass sie linear ist und die Leibniz-Regel erfüllt. (also dass diese kovariante Ableitung die obige Tensordefinition erfüllt), sowie dass sie linear ist und die Leibniz-Regel erfüllt.
Durch die Forderung  (hierbei bezeichnet g_mn die Komponenten des metrischen Tensors) (hierbei bezeichnet g_mn die Komponenten des metrischen Tensors)
und die Forderung der Torsionsfreiheit wird dann abgeleitet, dass die Komponenten von Gamma durch die Christoffelsymbole gegeben sind.
Diese ganze Konstruktion kann ich sehr gut nachvollziehen und leuchtet mir ein. Mir leuchtet es aber nicht ein, wie ich das jetzt einordnen soll, bzw. wie ich das unter einen Hut bringen soll mit der Tatsache, dass die Tensorkomponenten ja eigentlich Skalare funktionen sind und daher eigentlich gilt  |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 02. Jan 2021 19:22 Titel: index_razor Verfasst am: 02. Jan 2021 19:22 Titel: |
 |
|
Ich denke die Ursache für deine Verwirrung liegt genau hier:
| Corbi hat Folgendes geschrieben: |
Durch die Forderung  (hierbei bezeichnet g_mn die Komponenten des metrischen Tensors) (hierbei bezeichnet g_mn die Komponenten des metrischen Tensors)
|
Nein, das kann nicht sein. Die Gleichung  ergibt nur im abstrakten Indexkalkül Sinn, in welchem ergibt nur im abstrakten Indexkalkül Sinn, in welchem  ein Tensor ist (derselbe Tensor wie ein Tensor ist (derselbe Tensor wie  etc.; die Indizes sind nur Dummies), aber nicht eine seiner Komponenten. Für die Komponenten gilt etc.; die Indizes sind nur Dummies), aber nicht eine seiner Komponenten. Für die Komponenten gilt
_{jn}=\partial_i g_{jn}-\Gamma^m_{ij}g_{mn}-\Gamma^s_{in}g_{sj}=0)
Vielleicht ist auch dies gemeint. Aber dann sind wir wieder bei der mehrdeutigen Schreibweise und es gilt meine Aussage über Texte, die nicht eindeutig definieren, wovon sie reden.
| Zitat: |
und die Forderung der Torsionsfreiheit wird dann abgeleitet, dass die Komponenten von Gamma durch die Christoffelsymbole gegeben sind.
Diese ganze Konstruktion kann ich sehr gut nachvollziehen und leuchtet mir ein. Mir leuchtet es aber nicht ein, wie ich das jetzt einordnen soll, bzw. wie ich das unter einen Hut bringen soll mit der Tatsache, dass die Tensorkomponenten ja eigentlich Skalare funktionen sind und daher eigentlich gilt  |
Du mußt lediglich den Unterschied zwischen _{mn}) und und ) verstehen. Das erste bezeichnet die mn-Komponente des Tensors verstehen. Das erste bezeichnet die mn-Komponente des Tensors  (ist also null, da der Tensor null ist). (ist also null, da der Tensor null ist).
Das zweite ist die kovariante Ableitung der Tensorkomponente  . Das ist dasselbe wie . Das ist dasselbe wie ) . Vielleicht wird es offensichtlicher wenn ich beides in dieselbe Gleichung schreibe? Die kovariante Konstanz von g lautet dann so: . Vielleicht wird es offensichtlicher wenn ich beides in dieselbe Gleichung schreibe? Die kovariante Konstanz von g lautet dann so:
_{jn}=\nabla_i (g_{jn})-\Gamma^m_{ij}g_{mn}-\Gamma^s_{in}g_{sj}=0) |
|
 |
Corbi
Anmeldungsdatum: 17.07.2018
Beiträge: 296
|
 Corbi Verfasst am: 02. Jan 2021 20:02 Titel: Corbi Verfasst am: 02. Jan 2021 20:02 Titel: |
 |
|
Ergibt dann die Gleichung:

im Ricci-Kalkül einen Sinn?
Und wie ist es bei den Christoffelsymbolen:
)
sind hierbei jetzt die Tensorkomponenten oder der Tensor im abstrakten Indexkalkül gemeint?
Noch eine Frage zu diesem abstrakten Indexkalkül: was bedeutet:
| Zitat: | | Das nennt sich abstrakte Indexnotation, d.h. die Indizes bezeichnen nicht die Komponenten des Tensors, sondern zeigen lediglich an, an welcher Stelle Vektoren bzw. Kovektoren erwartet werden. |
also was meinst du mit "an welche Stelle Vektoren...erwartet werden" ? |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 02. Jan 2021 20:15 Titel: index_razor Verfasst am: 02. Jan 2021 20:15 Titel: |
 |
|
| Corbi hat Folgendes geschrieben: | Ergibt dann die Gleichung:

im Ricci-Kalkül einen Sinn?
|
Ja, wenn man in bezug auf die Notation etwas nachsichtig ist und die linke Seite als ^j) interpretiert. Wenn man sie als kovariante Ableitung der Vektorkomponente interpretiert. Wenn man sie als kovariante Ableitung der Vektorkomponente  interpretiert, was mit Sicherheit nicht gemeint ist, dann wäre sie falsch. interpretiert, was mit Sicherheit nicht gemeint ist, dann wäre sie falsch.
| Zitat: |
Und wie ist es bei den Christoffelsymbolen:
)
sind hierbei jetzt die Tensorkomponenten oder der Tensor im abstrakten Indexkalkül gemeint?
|
Es kann beides gemeint sein. Das muß der Autor definieren.
| Zitat: |
Noch eine Frage zu diesem abstrakten Indexkalkül: was bedeutet:
| Zitat: | | Das nennt sich abstrakte Indexnotation, d.h. die Indizes bezeichnen nicht die Komponenten des Tensors, sondern zeigen lediglich an, an welcher Stelle Vektoren bzw. Kovektoren erwartet werden. |
also was meinst du mit "an welche Stelle Vektoren...erwartet werden" ? |
Tensoren kann man sich als multilineare Abbildungen vorstellen, die Vektoren oder Kovektoren als Argumente erwarten. Ein Tensor T der Stufe (1,1) z.b. "erwartet" einen Vektor  , einen Kovektor , einen Kovektor  und ergibt dann eine Zahl, sagen wir und ergibt dann eine Zahl, sagen wir
\mapsto T(X,\omega).)
Im abstrakten Indexkalkül drückt man dies aus, indem man  (statt einfach T) schreibt. Die Zahl (statt einfach T) schreibt. Die Zahl ) ergibt sich aus der Kontraktion ergibt sich aus der Kontraktion
 |
|
 |
Corbi
Anmeldungsdatum: 17.07.2018
Beiträge: 296
|
 Corbi Verfasst am: 02. Jan 2021 20:38 Titel: Corbi Verfasst am: 02. Jan 2021 20:38 Titel: |
 |
|

hm also mir leuchtet es noch nicht so ganz ein, warum das keinen Sinn ergeben soll. Die erste Gleichheit kann ich ja im Prinzip einfach als Definition von dem Ausdruck 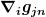 betrachten (mit g_jn als Tensorkomponente). Wenn man da jetzt kosequent überall (auch in den Christoffelsymbolen) die g_ij als Komponenten des metrischen Tensors interpretiert, kann man recht leicht zeigen, dass dieser Ausdruck 0 ergibt. betrachten (mit g_jn als Tensorkomponente). Wenn man da jetzt kosequent überall (auch in den Christoffelsymbolen) die g_ij als Komponenten des metrischen Tensors interpretiert, kann man recht leicht zeigen, dass dieser Ausdruck 0 ergibt.
Mir leuchtet dieses abstrakte Indexkalkül immernoch nicht ein.  sind dabei a und b jetzt Indizes die Werte von 0 bis sind dabei a und b jetzt Indizes die Werte von 0 bis
3 annehmen können? |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 02. Jan 2021 21:07 Titel: index_razor Verfasst am: 02. Jan 2021 21:07 Titel: |
 |
|
| Corbi hat Folgendes geschrieben: | 
hm also mir leuchtet es noch nicht so ganz ein, warum das keinen Sinn ergeben soll.
|
Das habe ich auch nicht gesagt. Im Gegenteil, ich schrieb, es ergäbe Sinn, wenn man in bezug auf die Notation etwas nachsichtig ist und die linke Seite als _{jn}) interpretiert. interpretiert.
 ist eine Tensorableitung. Sie ordnet also jedem Tensor T einen weiteren Tensor ist eine Tensorableitung. Sie ordnet also jedem Tensor T einen weiteren Tensor  zu. Der Sinn von zu. Der Sinn von  ist also entweder die jn-Komponente des Tensors ist also entweder die jn-Komponente des Tensors  oder dieser Tensor selbst. oder dieser Tensor selbst.
| Zitat: |
Mir leuchtet dieses abstrakte Indexkalkül immernoch nicht ein.  sind dabei a und b jetzt Indizes die Werte von 0 bis sind dabei a und b jetzt Indizes die Werte von 0 bis
3 annehmen können? |
Nein, sie zeigen nur an, welche Argumente des Tensors Vektoren und welche Kovektoren sind, bzw. anders formuliert mit welchen davon man an welcher Stelle den Tensor T kontrahieren kann. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 02. Jan 2021 21:18 Titel: index_razor Verfasst am: 02. Jan 2021 21:18 Titel: |
 |
|
P.S.
| Corbi hat Folgendes geschrieben: | 
hm also mir leuchtet es noch nicht so ganz ein, warum das keinen Sinn ergeben soll. Die erste Gleichheit kann ich ja im Prinzip einfach als Definition von dem Ausdruck 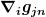 betrachten (mit g_jn als Tensorkomponente). betrachten (mit g_jn als Tensorkomponente). |
Dann führt man genau die Mehrdeutigkeit ein, von der ich die ganze Zeit rede. Die Tensorableitung  hat die Eigenschaft hat die Eigenschaft

für alle Funktionen f.
Falls, wie du voraussetzt,  die jn-Komponente von g sein soll, folgt also andererseits die jn-Komponente von g sein soll, folgt also andererseits

Und damit muß man sich wieder wundern wie diese Eigenschaft mit deiner "Definition" zu vereinbaren ist. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18062
|
 TomS Verfasst am: 03. Jan 2021 08:46 Titel: TomS Verfasst am: 03. Jan 2021 08:46 Titel: |
 |
|
| Corbi hat Folgendes geschrieben: | 
hm also mir leuchtet es noch nicht so ganz ein, warum das keinen Sinn ergeben soll. Die erste Gleichheit kann ich ja im Prinzip einfach als Definition von dem Ausdruck 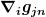 betrachten (mit betrachten (mit  als Tensorkomponente). als Tensorkomponente). |
Im Sinne der abstrakten Indexnotation ist aber genau nicht  als Tensorkomponente gemeint. Wenn als Tensorkomponente gemeint. Wenn  als Tensorkomponente aufzufassen wäre, dann wäre als Tensorkomponente aufzufassen wäre, dann wäre  einfach eine Funktion. Bzgl. einer Funktion einfach eine Funktion. Bzgl. einer Funktion

gilt jedoch

und das ist hier nicht gemeint, denn erstens liegen 16 Funktionen vor, die nach Ableitung wieder zu einem Tensor zusammengefasst werden sollen, und zweitens kann in

nicht eine Funktion gemeint sein, da vermöge der Summation mehrere Indizes und somit mehrere Funktionen auftreten.
Deswegen bedeutet die abstrakte Indexnotation bei  zunächst nicht, dass für ein spezielles Indexpaar j,n eine Komponente zu betrachten ist, sondern dass bei dem Objekt zunächst nicht, dass für ein spezielles Indexpaar j,n eine Komponente zu betrachten ist, sondern dass bei dem Objekt  als Ganzes ein Tensor zweiter Stufe vorliegt. Sobald dies klar ist, wird dies nie als eine Funktion aufgefasst sondern es wird immer als ein Objekt „Tensor zweiter Stufe“ verstanden, mit kovariante Ableitung als Ganzes ein Tensor zweiter Stufe vorliegt. Sobald dies klar ist, wird dies nie als eine Funktion aufgefasst sondern es wird immer als ein Objekt „Tensor zweiter Stufe“ verstanden, mit kovariante Ableitung

Und natürlich kannst du zuletzt auch

einsetzen. Die Notation leistet beides, allerdings um den Preis, dass du wissen musst, wann du etwas tust.
@index_razor: ich weiß, was du mit
„Die Tensorableitung hat die Eigenschaft

für alle Funktionen f meinst, aber ich halte das in diesem Zusammenhang für verwirrend.
Der Physiker lernt dies für „skalare Funktionen“ sowie dass „eine Komponente eines Tensors keine skalare Funktion ist“. Damit käme er nie auf die Idee,  in deinem Sinne als eine Funktion aufzufassen. in deinem Sinne als eine Funktion aufzufassen.
Deinen Beitrag vom 29. halte ich für eine sehr schöne Zusammenfassung, auch wenn die Brücke zur abstrakten Indexnotation offenbar noch nicht wirklich klar wird.
Zu
| index_razor hat Folgendes geschrieben: | Die wichtige Nachricht ist lediglich, daß die Definition
)
überhaupt keine kovariante Ableitung benötigt, also auch erst recht keinen Levi-Civita-Zusammenhang. |
Das kannst du vermöge deines Zugangs so sagen. Wenn dieser Zugang jedoch nicht verwendet wird, dann funktioniert dies grade nicht, dann muss umgekehrt der Laplace-Operator mittels kovarianter Ableitungen definiert werden. Und im Rahmen der theoretischen Physik geschieht dies eben sehr häufig direkt mittels des Levi-Cevita-Zusammenhang. Natürlich kann man für diesen Spezialfall die Äquivalenz zeigen, d.h. man startet eben gerade mit den kovarianter Ableitungen gemäß des Levi-Cevita-Zusammenhangs und leitet die zitierte Formel ab. Es sind Äquivalenzumformungen, die ich in beide Richtungen lesen kann.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
|
|















