| Induktion - veränderliche Fläche bestimmen |
| Autor | Nachricht | |||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Maxwell90 Anmeldungsdatum: 19.06.2018 Beiträge: 78 |
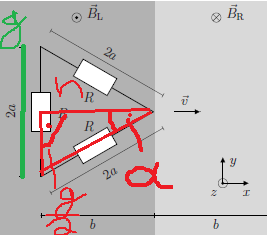
|
|||||||||||||||||||
| Myon Anmeldungsdatum: 04.12.2013 Beiträge: 5852 |
|
|||||||||||||||||||
| Maxwell90 Anmeldungsdatum: 19.06.2018 Beiträge: 78 |
|
|||||||||||||||||||
| Myon Anmeldungsdatum: 04.12.2013 Beiträge: 5852 |
|
|||||||||||||||||||
| Maxwell90 Anmeldungsdatum: 19.06.2018 Beiträge: 78 |
|
|||||||||||||||||||
| Myon Anmeldungsdatum: 04.12.2013 Beiträge: 5852 |
|
|||||||||||||||||||
| Maxwell90 Anmeldungsdatum: 19.06.2018 Beiträge: 78 |
|
|||||||||||||||||||
| Maxwell90 Anmeldungsdatum: 19.06.2018 Beiträge: 78 |
|
|||||||||||||||||||
| Maxwell90 Anmeldungsdatum: 19.06.2018 Beiträge: 78 |
|
|||||||||||||||||||
| Myon Anmeldungsdatum: 04.12.2013 Beiträge: 5852 |
|
|||||||||||||||||||
| Verwandte Themen - die Neuesten | |||||
| Themen | Antworten | Autor | Aufrufe | Letzter Beitrag | |
|---|---|---|---|---|---|
 |
Planetenbewegung: Aphel bestimmen | 2 | Ortus | 534 | 05. März 2024 19:33 Myon |
 |
Bandlücke von Germanium bestimmen | 0 | TryingToUnderstandIt | 814 | 01. Feb 2024 13:39 TryingToUnderstandIt |
 |
Strahldurchmesser bestimmen Gaußscher Strahl | 3 | Hase mit den Ohren | 1150 | 12. Jan 2024 16:44 gast001 |
 |
Doppelstern-Umlaufzeit bestimmen | 6 | Gast | 872 | 06. Dez 2023 21:59 TomS |
 |
Winkel bestimmen, sodass die Seilkraft minimal wird | 2 | Xaraua | 855 | 05. Dez 2023 14:24 roycy |
| Verwandte Themen - die Größten | |||||
| Themen | Antworten | Autor | Aufrufe | Letzter Beitrag | |
|---|---|---|---|---|---|
 |
Aufgaben zur Induktion | 60 | Ricky | 35025 | 27. Jan 2009 15:54 Ricky |
 |
Vollständige Induktion | 54 | Ricky | 18252 | 18. Okt 2010 14:22 Ricky |
 |
Rollmopswickelmaschine (Induktion, Lorentzkraft) | 49 | Ricky | 21256 | 10. März 2009 16:19 Ricky |
 |
Elektrischer Champagner-Rührer (Induktion, Lorentzkraft) | 48 | Ricky | 14572 | 10. März 2009 16:18 Ricky |
 |
Berechnung Fläche Körper | 38 | Mark21 | 2844 | 17. Mai 2022 12:05 as_string |
| Verwandte Themen - die Beliebtesten | |||||
| Themen | Antworten | Autor | Aufrufe | Letzter Beitrag | |
|---|---|---|---|---|---|
 |
Beschleunigung durch Ableiten bestimmen | 5 | corona | 95604 | 25. Okt 2008 18:06 corona |
 |
Packungsdichte von Gittern bestimmen. | 6 | Blub | 51450 | 27. Apr 2006 19:53 as_string |
 |
gleichmäßige Beschleunigung, Weg aus v-t-Diagramm bestimmen | 9 | DQ12 | 46514 | 21. Jun 2007 18:22 -Anja- |
 |
Bestimmen von Wellenlänge durch Beugung am Gitter | 21 | würmchen | 41048 | 23. Feb 2005 18:11 würmchen |
 |
Induktion- Was ist das und wie funktioniert das? | 12 | padori | 36154 | 29. März 2010 18:00 planck1858 |