Form des B-Feldes eines unendlich langen, geraden Stroms

Nestor · Anmeldungsdatum: 01.03.2019 Beiträge: 1

Meine Frage:
Angeblich ist es möglich, die Form des B-Feldes eines unendlich langen, geraden Stromes einzig aus Symmetrieüberlegungen herzuleiten. Mir selbst gelingt dies allerdings nur für die tangentiale und die radiale Feldkomponente. Mir gelingt es jedoch seit Tagen nicht, Argumente zur Bestimmung der Feldkomponente parallel zur Stromflussrichtung zu finden. Auch die mir zugängliche Literatur schweigt zu dieser Frage. Es wird einfach "Symmetrie" gesagt und weitergegangen. Dies ist natürlich keine hinreichende Begründung.

Meine Ideen:
Ich möchte kurz darstellen, was ich mir mit eigenem Nachdenken klar machen konnte:
Ich wähle ein zylindrisches Koordinatensystem so, dass der unendlich lange, gerade und zeitlich konstante Strom in der z-Achse liegt und in positiver z-Richtung fliesst. In diesen Koordinaten können wir das B-Feld ausdrücken als

Weil sich nichts physikalisch Relevantes ändert, wenn wir die Situation um die z-Achse drehen oder entlang der z-Achse verschieben, es aber einen geometrischen Unterschied macht, wie weit wir uns von der z-Achse befinden, können wir schreiben:

Zu sehen, wie genau

von r abhängt ist trivial (Ampere'sches Gesetz) und interessiert an dieser Stelle nicht. Für die Bestimmung von

können wir folgende Überlegung anstellen:

sei die Radialkomponente, die sich beim Fliessen des Stromes in positiver z-Richtung einstellt. Nun lassen wir einen Strom des selben Betrages in negativer Richtung fliessen. Für die sich daraus ergebende Radialkomponente

folgt wegen der Linearität des elektromagnetischen Feldes

Nun bewerkstelligen wir diese Stromumkehr, indem wir den Strom so im Raum drehen, so dass der Strom wieder in der z-Achse liegt, aber in negativer Richtung fliesst. Diese Drehung verändert die Radialkomponente nicht, und somit gilt

und damit

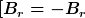
Daraus folgt

Damit sind zwei von drei Komponenten bestimmt. Aber bei B_{z} komme ich auch nach Tagen des Nachdenkens nicht weiter. Ich konnte mir lediglich klar machen, dass

konstant sein muss. Ich konnte kein Argument finden, mit dem ich

finden kann (was ja die richtige Antwort wäre, aber warum?!). Ich brauche Eure Hilfe, wie es scheint. Bitte beachtet, dass versuche, eine Antwort auf der Basis von Symmetrieüberlegungen zu finden, so wie es angeblich ja möglich sein soll. Also bitte keine Argumente, die z.B. das Biot-Savart Gesetz bemühen. Vielen Dank für die hoffentlich folgende Diskussion!

Willkommen im Physikerboard!
Ich habe Deine LaTeX-Enad-Tags korrigiert (/latex statt \latex).
Viele Grüße
Steffen

Myon · Anmeldungsdatum: 04.12.2013 Beiträge: 5870

Nehmen wir wieder an, der Strom fliesse in z-Richtung. Aus

folgt

Aus „Symmetriegründen“ müssen sicher

und

gleich 0 sein. Wäre jetzt

, so müsste wegen

und

die

-Komponente im ganzen Raum konstant sein, was nicht sein kann. Das B-Feld muss im Unendlichen verschwinden, wenn die Energie des Magnetfeldes pro Längeneinheit des Leiters beschränkt sein soll.

Nestor2 · Gast

Hey Myon,
vielen Dank! Anfangs hatte ich Zweifel, weil ja nicht alle Felder im unendlichen verschwinden (z.B. das Feld eines unendlich ausgedehnten, konstanten Ebenenstromes). Aber Du sagst ja: wenn die Energie pro Längeneinheit endlich ist, und diese Bedingung ist bei der unendlichen Stromebene ja verletzt. Oder man könnte noch anders sehen, dass Dein Antwort korrekt ist: es geht ja hier strikt linear zu. Also müssen alle Feldkomponenten mit dem gleichen Faktor skalieren. Da die Tangetialkomponente umgekehrt proportional zum Radialabstand ist, geht diese im Unendlichen gegen 0. Also geht auch die z-Komponente im unendlichen gegen 0. Da die z-Komponente wie von Dir gezeigt (und von mir auch selbst erkannt) konstant ist, ist sie überall gleich 0.
Vielen Dank für Deine super Antwort!