| Autor |
Nachricht |
Systemdynamiker
Anmeldungsdatum: 22.10.2008
Beiträge: 594
Wohnort: Flurlingen
|
 Systemdynamiker Verfasst am: 10. Feb 2019 10:02 Titel: Kann Entropie strömen? Systemdynamiker Verfasst am: 10. Feb 2019 10:02 Titel: Kann Entropie strömen? |
 |
|
Kann Entropie von einem Körper zu einem andern strömen?
Begründung eines Physikers: "Die Entropie hängt nicht nur von der zu verteilenden Energie ab, sondern auch von der Anzahl der Freiheitsgrade und der Lage der zu den Freiheitsgraden gehörenden quantenmechanischen Energieniveaus. Während Energie in Form von Wärme zwischen zwei thermodynamischen Systemen ausgetauscht werden kann, sind Anzahl der Freiheitsgrade und quantenmechanische Eigenschaften des Systems nicht transferierbar. Richtig ist: Im thermischen Kontakt strömt Wärme. Durch die Verringerung der inneren Energie des wärmeabgebenden Systems nimmt dessen Entropie ab, die Entropie des wärmeaufnehmenden Systems nimmt zu. Von einem Entropiestrom zu sprechen ist sinnlos, da die systemimmanenten Eigenschaften – Zahl und Art der Freiheitsgrade und Lage der Energieniveaus – nicht strömen können."
Ist diese Begründung stichhaltig?
_________________
Herzliche Grüsse Werner Maurer |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18016
|
 TomS Verfasst am: 10. Feb 2019 10:35 Titel: Re: Kann Entropie strömen? TomS Verfasst am: 10. Feb 2019 10:35 Titel: Re: Kann Entropie strömen? |
 |
|
| Systemdynamiker hat Folgendes geschrieben: | Kann Entropie von einem Körper zu einem andern strömen?
Begründung eines Physikers: "Die Entropie hängt nicht nur von der zu verteilenden Energie ab, sondern auch von der Anzahl der Freiheitsgrade und der Lage der zu den Freiheitsgraden gehörenden quantenmechanischen Energieniveaus. Während Energie in Form von Wärme zwischen zwei thermodynamischen Systemen ausgetauscht werden kann, sind ... Freiheitsgrade ... nicht transferierbar. ... Von einem Entropiestrom zu sprechen ist sinnlos, da die systemimmanenten Eigenschaften – Zahl und Art der Freiheitsgrade und Lage der Energieniveaus – nicht strömen können."
Ist diese Begründung stichhaltig? |
Ist sie natürlich nicht, und ich wüsste auch nicht, wer sie so äußern sollte.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
ML
Anmeldungsdatum: 17.04.2013
Beiträge: 3388
|
 ML Verfasst am: 10. Feb 2019 10:41 Titel: Re: Kann Entropie strömen? ML Verfasst am: 10. Feb 2019 10:41 Titel: Re: Kann Entropie strömen? |
 |
|
Hallo,
| Systemdynamiker hat Folgendes geschrieben: | | Kann Entropie von einem Körper zu einem andern strömen? |
Beim Strömen denkt man intuitiv an eine Größe, die im System erhalten bleibt. Das ist bei Entropie im Allgemeinen nicht der Fall.
Wenn wir uns den 2. Hauptsatz für ein System anschauen:
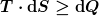 , ,
so kann ich mich bei der Gültigkeit des Gleichheitszeichens (Zustandsänderung verläuft durch Gleichgewichtszustände) durchaus vorstellen, von einer strömenden Entropie zu sprechen. Bei Gültigkeit des Ungleichheitszeichens hat man m. E. eine Strömung und eine Generierung gleichzeitig.
Viele Grüße
Michael |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18016
|
 TomS Verfasst am: 10. Feb 2019 11:16 Titel: TomS Verfasst am: 10. Feb 2019 11:16 Titel: |
 |
|
Was man vermeiden sollte ist, zu versuchen, irgendein mikroskopisches Bild zu entwickeln. Wenn man auf Ebene der Quantenmechanik reine Zustände betrachten kann, ist deren Entropie immer exakt Null. Der Begriff der Entropie ist immer nur bei einer „Vergröberung“ sinnvoll.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Systemdynamiker
Anmeldungsdatum: 22.10.2008
Beiträge: 594
Wohnort: Flurlingen
|
 Systemdynamiker Verfasst am: 11. Feb 2019 09:54 Titel: Physik an Unis Systemdynamiker Verfasst am: 11. Feb 2019 09:54 Titel: Physik an Unis |
 |
|
Das von mir aufgeführte Zitat entstammt dem Brief eines Physikprofessors einer Uni an den Rektor eines Gymnasiums. Ich habe mir über mehr als eine Stunde dessen mündliche Begründung angehört: für die Entropie kann man keine Kontinuumsgleichung formulieren, weil die Entropie keine Erhaltungsgrösse ist; beim Hände reiben entsteht keine Entropie; Wärme ist die potentielle und kinetische Energie der Moleküle; Entropie ist so kompliziert, dass ich diese Grösse selber nicht ganz verstehe.
Nichts gegen eine mikroskopische Beschreibung, wenn sie korrekt ausgeführt wird. Der Zusammenhang zwischen quantenmechanischem Messprozess und Entropie scheint mir ein sehr interessantes Thema zu sein. Für Schülerinnen und Schüler ist die mikroskopische Deutung dagegen eher ungeeignet. Um das Problem zu vereinfachen, macht man meist nur eine Statistik im Ortsraum statt im Phasenraum und erklärt die Entropie zu einem Mass für die Unordnung. So entsteht natürlich keine Verständnis für die Funktionsweise einer Wärmepumpe. Einige Ideen dazu habe ich in einem Video dargelegt: https://youtu.be/De45koXFbh0
_________________
Herzliche Grüsse Werner Maurer |
|
 |
ML
Anmeldungsdatum: 17.04.2013
Beiträge: 3388
|
 ML Verfasst am: 11. Feb 2019 10:48 Titel: Re: Physik an Unis ML Verfasst am: 11. Feb 2019 10:48 Titel: Re: Physik an Unis |
 |
|
Hallo,
| Systemdynamiker hat Folgendes geschrieben: | | beim Hände reiben entsteht keine Entropie; |
wieso nicht?
Viele Grüße
Michael |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 11. Feb 2019 12:17 Titel: Re: Physik an Unis index_razor Verfasst am: 11. Feb 2019 12:17 Titel: Re: Physik an Unis |
 |
|
| Systemdynamiker hat Folgendes geschrieben: | | Das von mir aufgeführte Zitat entstammt dem Brief eines Physikprofessors einer Uni an den Rektor eines Gymnasiums. Ich habe mir über mehr als eine Stunde dessen mündliche Begründung angehört: für die Entropie kann man keine Kontinuumsgleichung formulieren, weil die Entropie keine Erhaltungsgrösse ist; |
Daß es sich nicht um eine Erhaltungsgröße handelt, schließt nicht aus, daß es eine Kontinuitätsgleichung gibt. Diese muß nur einen Term für die Quellendichte beinhalten, z.B.
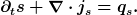
Die Quellendichte auf der rechten Seite muß hier natürlich irgendwie physikalisch modelliert werden. (Dasselbe gilt aber letztendlich auch für die Stromdichte.) In der Hydrodynamik begegnet man oft Kontinuumsbeschreibungen der Entropie mit den zugehörigen Entropieströmen.
| Zitat: |
Wärme ist die potentielle und kinetische Energie der Moleküle;
|
Nein, das ist die innere Energie, nicht die Wärme. Eine Unterscheidung von "Wärme" und anderen Energieformen ist nur sinnvoll, wenn man Änderungen der inneren Energie betrachtet. Wärme ist der Teil der Änderung der inneren Energie, der sich auf die Änderung der Besetzungswahrscheinlichkeiten fester Energieniveaus zurückführen läßt. Im Gegensatz dazu ist Arbeit z.B. der Teil, der eine Änderung besetzter Energieniveaus selbst bewirkt unter Beibehaltung ihrer Besetzungswahrscheinlichkeiten. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18016
|
 TomS Verfasst am: 11. Feb 2019 18:37 Titel: TomS Verfasst am: 11. Feb 2019 18:37 Titel: |
 |
|
Eine Entropiestromdichte kenne ich nicht.
Sie macht aus meiner Sicht nicht unbedingt Sinn: Entropie ist im thermodynamischen Gleichgewicht definiert; dann ist eine Dichte = eine lokale ohnehin unnötig; andersherum: wenn kein thermodynamisches Gleichgewicht vorliegt und damit keine Entropie definiert werden kann, dann wäre wiederum eine Dichte angemessen.
Zweiter Punkt: eine Dichte suggeriert eine mikroskopische Beschreibung; diese ist für die Entropie in gewisser Weise sinnlos, weil sie erst durch Vergröberung der mikroskopischen zur makroskopischen Sicht entsteht, d.h. z.B. durch Ausspuren von Freiheitsgraden.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18016
|
 TomS Verfasst am: 11. Feb 2019 18:44 Titel: Re: Physik an Unis TomS Verfasst am: 11. Feb 2019 18:44 Titel: Re: Physik an Unis |
 |
|
| Systemdynamiker hat Folgendes geschrieben: | | Nichts gegen eine mikroskopische Beschreibung, wenn sie korrekt ausgeführt wird. Der Zusammenhang zwischen quantenmechanischem Messprozess und Entropie scheint mir ein sehr interessantes Thema zu sein. |
M.E. gibt es keinen. Die Definition der Entropie erfolgt ohne Betrachtung des Messprozesses. Ein Messprozess mit einem nicht-quantenmechanischen Messgerät und -prozess führt sofort zu Problemen (siehe Kollaps etc.). Im Falle einer rein quantenmechanischen Betrachtung des Messprozesses ist die Entropie immer exakt Null. Andersherum: nicht-verschwindende Entropie resultiert im Rahmen der Quantenmechanik durch Ausspuren von Freiheitsgraden, nicht durch einen Messprozess.
| Systemdynamiker hat Folgendes geschrieben: | | Für Schülerinnen und Schüler ist die mikroskopische Deutung dagegen eher ungeeignet. Um das Problem zu vereinfachen, macht man meist nur eine Statistik im Ortsraum statt im Phasenraum und erklärt die Entropie zu einem Mass für die Unordnung. |
Wenn man Entropie als Unordnung auffasst, ist dies natürlich bereits eine mikroskopische Deutung. Andersherum: wenn man ein thermodynamisches System ausschließlich als Punkt im Phasenraum begreift, kann und darf man Entropie nicht als Unordnung auffassen. Die Darstellung ist da oft inkonsistent.
Ich halte die mikroskopische Deutung auch nicht für ungeeignet, man muss es nur richtig machen.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 11. Feb 2019 21:36 Titel: index_razor Verfasst am: 11. Feb 2019 21:36 Titel: |
 |
|
| TomS hat Folgendes geschrieben: | Eine Entropiestromdichte kenne ich nicht.
Sie macht aus meiner Sicht nicht unbedingt Sinn: Entropie ist im thermodynamischen Gleichgewicht definiert; dann ist eine Dichte = eine lokale ohnehin unnötig; |
Hältst du die Aussage für sinnvoll, daß gerade in verschiedenen Regionen der Erde sehr unterschiedliche Temperaturen herrschen, obwohl Temperatur nur im thermodynamischen Gleichgewicht definiert ist? Konduktive Wärmeströme werden ganz selbstverständlich mit Hilfe von Temperaturgradienten beschrieben.
| Zitat: |
andersherum: wenn kein thermodynamisches Gleichgewicht vorliegt und damit keine Entropie definiert werden kann, dann wäre wiederum eine Dichte angemessen.
|
Entropie kann für beliebige gemischte Zustände, bzw. klassische Phasenraumverteilungen 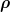 definiert werden, unabhängig davon ob sie ein thermodynamisches Gleichgewicht beschreiben oder nicht; eine Entropiedichte oder -stromdichte allerdings nur in spezielleren Situationen. definiert werden, unabhängig davon ob sie ein thermodynamisches Gleichgewicht beschreiben oder nicht; eine Entropiedichte oder -stromdichte allerdings nur in spezielleren Situationen.
Die Hydrodynamik basiert allgemein auf der Betrachtung lokaler Gleichgewichte in Fluidelementen, die zwar makroskopisch, aber trotzdem klein im Vergleich zum Gesamtsystem sind. Sie befinden sich quasi mit sich selbst, aber nicht mit den umgebenden Fluidelementen im Gleichgewicht. Deshalb können sie untereinander Wärme und Entropie austauschen.
Unter diesen Bedingungen kann man eine Entropiestromdichte definieren und tut das auch.
| Zitat: |
Zweiter Punkt: eine Dichte suggeriert eine mikroskopische Beschreibung; diese ist für die Entropie in gewisser Weise sinnlos, weil sie erst durch Vergröberung der mikroskopischen zur makroskopischen Sicht entsteht, d.h. z.B. durch Ausspuren von Freiheitsgraden. |
Eine Dichte suggeriert für dich eine mikroskopische Beschreibung? "Dichte" ist ein Begriff der Kontinuumsmechanik. Diese liefert bestenfalls eine effektive makroskopische Beschreibung der Materie auf Skalen, die groß genug sind um die atomare und molekulare "Körnigkeit" vernachlässigen zu können.
Die einzelnen Fluidelemente bestehen aus einer großen Anzahl an Molekülen, deswegen kann man sie mit den Methoden der statistischen Mechanik behandeln. Andererseits macht jedes von ihnen nur einen kleinen Teil des Gesamtsystems aus. Man kann also jedem von ihnen einen eigenen Makrozustand zuordnen, der nicht mit allen anderen übereinstimmen muß. Das ergibt effektive eine Ortsabhängigkeit der thermodynamischen Größen.
Zuletzt bearbeitet von index_razor am 11. Feb 2019 22:27, insgesamt einmal bearbeitet |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 11. Feb 2019 22:21 Titel: index_razor Verfasst am: 11. Feb 2019 22:21 Titel: |
 |
|
Es war nicht so einfach eine Internetquelle zu finden, aber in Gl. 7.32 in diesem pdf findet sich eine lokale Bilanzgleichung für die Entropie eines Fluids. Diese hat die Form aus meinem ursprünglichen Beitrag: 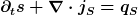 (allerdings ist (allerdings ist  normalerweise als "Entropie pro Masse" definiert, deswegen ist die Entropiedichte normalerweise als "Entropie pro Masse" definiert, deswegen ist die Entropiedichte 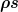 , und nicht , und nicht  ) )
Es gibt einen konvektiven Entropiestrom 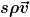 , sowie einen konduktiven Strom , sowie einen konduktiven Strom
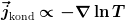 . .
Auf der rechten Seite steht die Quellendichte mit einem Term
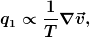
der die Reibung relativ zueinander bewegter Fluidelemente beschreibt und einem Term
^2)
der auf die Wärmeleitung zwischen den Teilen des Fluides zurückzuführen ist. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18016
|
 TomS Verfasst am: 12. Feb 2019 00:07 Titel: TomS Verfasst am: 12. Feb 2019 00:07 Titel: |
 |
|
Danke für die Recherche und den Link.
Du hast natürlich recht, innerhalb eines genügend kleinen jedoch nicht verschwindenden Volumen kann man tatsächlich von thermodynamischem Gleichgewicht, Temperatur und Entropie sprechen, auch wenn das System als Ganzes sich nicht im Gleichgewicht befindet.
Und ja, du hast recht, die quantenmechanische Definition der Entropie nach von Neumann gilt auch abseits des thermodynamischen Gleichewichtes.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Systemdynamiker
Anmeldungsdatum: 22.10.2008
Beiträge: 594
Wohnort: Flurlingen
|
 Systemdynamiker Verfasst am: 12. Feb 2019 09:47 Titel: Danke Systemdynamiker Verfasst am: 12. Feb 2019 09:47 Titel: Danke |
 |
|
Vielen Dank an alle für die konstruktiven Rückmeldungen. Der Link von index_razor war sehr hilfreich (im entsprechenden Ordner findet man sogar das ganze Skript). Die Betrachtungsweise aus der Fluiddynamik kann in den Elementarunterricht zurück übersetzt werden. Statt Dichte und Stromdichte nimmt man dann konzentrierte Systeme mit Inhalt und Stromstärke.
Interessant an dieser Diskussion ist der Umstand, dass man die Unverträglichkeit zwischen mikroskopischer und makroskopischer Beschreibung meist nur bei der Entropie thematisisiert. Dabei gibt es diesen Modellkonflikt bei jeder bilanzierfähigen Menge. Nimmt man die Dichte des elektrischen Stromes in einem Halbleiter, kann man analog argumentieren. Stoffmenge und Drehimpuls sind weitere konfliktträchtige Grössen, wobei bei der ersten die mikroskopische Definition inhärent ist und bei der zweiten die Nichtlokalisierbarkeit ein Problem darstellt. Trotzdem findet man in der Literatur für beide Grössen die Kontinuitätsgleichung.
_________________
Herzliche Grüsse Werner Maurer |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18016
|
 TomS Verfasst am: 12. Feb 2019 20:13 Titel: Re: Danke TomS Verfasst am: 12. Feb 2019 20:13 Titel: Re: Danke |
 |
|
| Systemdynamiker hat Folgendes geschrieben: | | Interessant an dieser Diskussion ist der Umstand, dass man die Unverträglichkeit zwischen mikroskopischer und makroskopischer Beschreibung meist nur bei der Entropie thematisisiert. |
Das alleine meinte ich nicht:
| TomS hat Folgendes geschrieben: | | Was man vermeiden sollte ist, zu versuchen, irgendein mikroskopisches Bild zu entwickeln. Wenn man auf Ebene der Quantenmechanik reine Zustände betrachten kann, ist deren Entropie immer exakt Null. Der Begriff der Entropie ist immer nur bei einer „Vergröberung“ sinnvoll. |
Natürlich kann man für viele Größen - auch für die Entropie - eine Bilanzgleichung für Volumina geeigneter Größe definieren; siehe auch die Richtigstellung seitens index_razor.
Trotzdem ist m.M.n. die Entropie anders geartet.
Betrachten wir zum Vergleich die Dichte, Ladungs- oder Stromdichte oder auch Energie- oder Impulsdichte. Derartige Größen werden mikroskopisch durch klassische Felder oder eben Wellenfunktionen bzw. lokale Feldoperatoren beschrieben. Letztere können auf beliebige Zustände angewandt werden, und man erhält in niedrigster Näherung wieder die Ausdrücke mittels klassischer Felder. Man findet Ausdrücke der Form
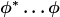
Die Entropie ist dagegen quantenmechanisch definiert als
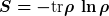
Ich sehe bzw. verstehe nicht, wie man daraus einen lokalen Operator gewinnen kann.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
|















