| Autor |
Nachricht |
Dieter5858
Moderator

Anmeldungsdatum: 02.08.2004
Beiträge: 696
Wohnort: Hamburg
|
 Dieter5858 Verfasst am: 05. Jan 2005 19:51 Titel: Was ist Entropie? Beispiel Kartenspiel? Dieter5858 Verfasst am: 05. Jan 2005 19:51 Titel: Was ist Entropie? Beispiel Kartenspiel? |
 |
|
Hi Leute
Ich hab den Begriff nun zwar auch schon mal gehört,
aber ich hab noch nicht so ganz begriffen was dieser "Wert"
Aussagt oder wozu er verwendet wird.
Das ganze hat ja irgendwas damit zu tun das die Möglichkeiten der Unordnung immer größer werden.
Kann mir das jemand nochmal Begreiflich erklären.
Vielleicht am Beispiel eines Kartenspieles, welches geordnet ist.
Wenn ich es mische nimmt nun die Entropie zu, warum? |
|
 |
AndyRo
Anmeldungsdatum: 27.12.2004
Beiträge: 22
Wohnort: Hamburg
|
 AndyRo Verfasst am: 05. Jan 2005 20:08 Titel: AndyRo Verfasst am: 05. Jan 2005 20:08 Titel: |
 |
|
Geh am besten auf www.wikipedia.de
Da ist es gut und ausfürlich und leicht verständlich erklärt.
MfG: AndyRo
_________________
- Wenn alle Stricke reißen, dann hänge ich mich auf - (Karl Krauss) |
|
 |
eXpli
Anmeldungsdatum: 05.01.2005
Beiträge: 42
|
 eXpli Verfasst am: 05. Jan 2005 20:19 Titel: eXpli Verfasst am: 05. Jan 2005 20:19 Titel: |
 |
|
Entropie ist ein Maß für die Unordnung in einem System.
Außerdem besagt hohe Entropie dass es viele mögliche Zustände gibt.
Für weiteres: www.wikipedia.de |
|
 |
umwälzer
Gast
|
 umwälzer Verfasst am: 17. Jan 2005 15:29 Titel: Re: Was ist Entropie umwälzer Verfasst am: 17. Jan 2005 15:29 Titel: Re: Was ist Entropie |
 |
|
| Dieter5858 hat Folgendes geschrieben: | Hi Leute
Ich hab den Begriff nun zwar auch schon mal gehört,
aber ich hab noch nicht so ganz begriffen was dieser "Wert"
Aussagt oder wozu er verwendet wird.
Das ganze hat ja irgendwas damit zu tun das die Möglichkeiten der Unordnung immer größer werden.
Kann mir das jemand nochmal Begreiflich erklären.
Vielleicht am Beispiel eines Kartenspieles, welches geordnet ist.
Wenn ich es mische nimmt nun die Entropie zu, warum? |
Die Entropie gilt nur für geschlossene Systeme ,nicht für offene,da
alle Systeme in der Natur offene Systeme sind,besteht die Möglichkeit davon auszugehen das das Universum auch offen ist,dh. die Aussage
das die Unordnung im Universum zunimmt gilt dann wohl nicht mehr,
wir sehen das die Natur immer neue Strukturen erschafft und evoltär
ist,gemäß dem linearem Denkschema der Thermodymik steuern
wir aber immer nur die Unordung zu und das ist einfach unlogisch,denn
sonst könnte die Natur keine höherwertigen sich ständig aufbauende Strukturen erschaffen,die Unordung ensteht dort wo alte Materie,abgestorbenes Leben zersetzt wird,sodas die Natur aus dessen
zersetzen Einzelbestandteile wieder neue Stoffgruppen,Ordnung erschafft. |
|
 |
umwälzer
Gast
|
 umwälzer Verfasst am: 17. Jan 2005 15:35 Titel: umwälzer Verfasst am: 17. Jan 2005 15:35 Titel: |
 |
|
Wenn meine These nicht stimmt,dann frag ich mal wie man Unordnung,
Ordnung denn nun definiert,in bezug auf Expansion,Kontraktion,Gravitation,Evolution,Implosion,Explosion in der
Frage ob einzelne Gruppen,vernetze Gruppen von Elementen/Materie/Stoffe,also vernetzt oder nicht vernetzt,biologisch
betrachtet. |
|
 |
Gast
|
 Gast Verfasst am: 17. Jan 2005 15:39 Titel: Re: Was ist Entropie Gast Verfasst am: 17. Jan 2005 15:39 Titel: Re: Was ist Entropie |
 |
|
| umwälzer hat Folgendes geschrieben: |
,gemäß dem linearem Denkschema der Thermodymik steuern
wir aber immer nur die Unordung zu und das ist einfach unlogisch,denn
sonst könnte die Natur keine höherwertigen sich ständig aufbauende Strukturen erschaffen,die Unordung ensteht dort wo alte Materie,abgestorbenes Leben zersetzt wird,sodas die Natur aus dessen
zersetzen Einzelbestandteile wieder neue Stoffgruppen,Ordnung erschafft. |
das bisschen Natur gleicht hier nichts aus, zumal dazu auch die Energiebilanz mit zu berücksichtigen ist. Ohne die Entropie der Sonne wär hier nichts mit Natur und Ordnung |
|
 |
MI
Anmeldungsdatum: 03.11.2004
Beiträge: 828
Wohnort: München
|
 MI Verfasst am: 17. Jan 2005 18:30 Titel: MI Verfasst am: 17. Jan 2005 18:30 Titel: |
 |
|
@umwälzer:
Wie gesagt. Wikipedia, da steht schon etwas drin.
Und ganz kurz: Ordnung=1/Unordnung (Entropie gleich Unordnung).
Der zweite Hauptsatz der Thermodynamik besagt: Die Entropie in einen irreversiblen System nimmt IMMMER zu, in einem reversiblen System kann sie auch konstant bleiben. Sie kann NICHT abnehmen.
Reversible Systeme: elastische Stösse zwischen wenigen Teilchen, einige kontrollierte Bewegungen
Irreversible Systeme: alles andere (also praktisch alles).
Aber wie wird der Begriff Ordnung und Unordnung eigentlich definiert?
Im Universum gibt es nur Energie in verschiedenen Formen. Alles ist Energie. Zustände mit niedriger Entropie (also geordnet) sind Energie in Masse, in Form von potentieller, chemischer oder kinetischer Energie.
Der Zustand mit hoher Entropie (ungeordnet) ist Wärme. Wenn also das ganze Universum nur noch aus Wärme besteht, dann ist der Entropiewert auf dem Höchstmöglichen.
Falls ich hier Mist erzähle, dann bitte schnell korrigieren, aber das ist die Definition und Erklärung, die ich kenne.
Gruss
MI |
|
 |
Gast
|
 Gast Verfasst am: 17. Jan 2005 18:46 Titel: Gast Verfasst am: 17. Jan 2005 18:46 Titel: |
 |
|
|
Ein bisschen Mist ist schon verträglich g |
|
 |
Dr.Oleg

Anmeldungsdatum: 25.01.2005
Beiträge: 98
Wohnort: Dresden
|
 Dr.Oleg Verfasst am: 25. Jan 2005 17:04 Titel: Dr.Oleg Verfasst am: 25. Jan 2005 17:04 Titel: |
 |
|
Kommentar von meinem Chemielehrer:
"Das brauchen Sie nicht zu verstehen, sie müssen nur die Formel kennen. Was die Entropie ist, dass versteh ich nicht, das verstehen nur die Quantenmechaniker."
_________________
Wenn der Weise auf die Sterne zeigt, sieht der Idiot nur den Finger...
In Foren betiteln sich manche Idioten mit Namen und akademischen Titeln, die sie in Wirklichkeit gar nicht besitzen. Das beste Beispiel ist "Dr. Oleg". |
|
 |
Dieter5858
Moderator

Anmeldungsdatum: 02.08.2004
Beiträge: 696
Wohnort: Hamburg
|
 Dieter5858 Verfasst am: 25. Jan 2005 18:17 Titel: Dieter5858 Verfasst am: 25. Jan 2005 18:17 Titel: |
 |
|
Hi Leute
Ahh endlich jemand der mir sagt das ich das nicht begreifen muss:-)
Mit Quantenphysik hab ich ja nix am Hut.
Aber kann jemand nochmal Versuchen das ganze am Beispiel eines Kartenspiel zu Erleutern.
Wenn ich also ein geordnetes Kartenspiel habe, und anfange es zu mischen, dann nimmt die Entropie zu.
Weil ich die Karten in einen ungeordneteren zusatnd bringe als sie vorher waren.
Aber ich kann ja trotzdem nicht vorhersagen welcher zusatnd der nächste ist.
Ob ich nun ein geordnetes oder ungeordnetes Kartenspiel nehme.
Oder ist das ein geschlossenes System oder was?
es gibt beim Kartenspiel ja eine Bestimmte Anzahl an möglichen zusammensetzung der Karten, und wenn ich die Karten mische wird sich diese Zahl ja nicht erhöhen.
Also ich habs noch net ganz verstanden... |
|
 |
para
Moderator

Anmeldungsdatum: 02.10.2004
Beiträge: 2874
Wohnort: Dresden
|
 para Verfasst am: 25. Jan 2005 18:25 Titel: para Verfasst am: 25. Jan 2005 18:25 Titel: |
 |
|
Unser Chemie-Lehrer (der gleiche wie bei "dr." oleg) hat uns das anhand einiger Runden Poker erklärt. Die unwahrscheinlichsten Kartenkombinationen (die mit der höchsten Ordnung) zählen am meisten, während die 0815-Kombis im Allgemeinen nichts bringen.
Die Zustände höherer Entropie sind also am wertlosesten und gleichzeitig am häufigsten ... Ist sicher nicht vollständig, aber für unsere Bedürfnisse war's gut  . .
_________________
Formeln mit LaTeX |
|
 |
Bruce
Anmeldungsdatum: 20.07.2004
Beiträge: 537
|
 Bruce Verfasst am: 26. Jan 2005 00:23 Titel: Bruce Verfasst am: 26. Jan 2005 00:23 Titel: |
 |
|
Ein Kartenspiel hat zunächst mal keine Entropie, egal ob die Karten
gemischt sind oder nicht. Allerdings kann man sich fragen, wie groß nach
dem Mischen die Wahrscheinlichkeit ist, daß die Karten gemäß einer
bestimmten Folge untereinander auf dem Stapel liegen. Wenn diese
Wahrscheinlichkeit für jede Folge gleich ist, dann ist das Kartenspiel
optimal gemischt, dann liegt der Zustand größtmöglicher Unbestimmtheit
oder meinetwegen der Zustand maximaler Unordnung vor. Man kann
jedoch eine Entropie 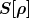 für die Wahrscheinlichkeitsverteilung für die Wahrscheinlichkeitsverteilung
) der möglichen Kartenfolgen der möglichen Kartenfolgen  nach dem Mischen definieren. nach dem Mischen definieren.
Diese Entropie ist ein Funktional (d.h. eine Funktion deren Argument
eine Funktion ist), das jeder sinnvollen Wahrscheinlichkeitsverteilung
für Kartenfolgen eine positive reelle Zahl zuordnet, die Entropie S. Das
Entropiefunktional S kann so definiert werden, daß 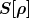 maximal wird, maximal wird,
wenn nach dem Mischen jede denkbare Kartenfolge gleichwahrscheinlich
ist, d.h. für den Zustand maximaler Unordnung. Für andere, speziellere
("geordnetere") Zustände nach dem Mischen wie z.B., wenn alle Karten
einer Sorte direkt untereinander liegen, würde das Entropiefunktional
einen kleineren Wert liefern.
Ein bekanntes Beispiel für ein Entropiefunktional eines Kartenspiels lautet
\,\ln\rho(a_i))
wobei der über alle mögichen Kartenfolgen auf dem Stapel summiert wird und
) die Wahrscheinlichkeit ist, nach dem speziellen Mischvorgang die die Wahrscheinlichkeit ist, nach dem speziellen Mischvorgang die
Kartenfolge  auf dem Stapel zu finden. Eine besondere Eigenschaft auf dem Stapel zu finden. Eine besondere Eigenschaft
dieses Entropiefunktionals ist seine Extensivität für hinreichend große
Kartenspiele, d.h. legt man zwei Stapel Karten übereinander, so ist
die Entropie dieses Stapels gleich der Summe der Entropien der beiden
einzelnen Stapel. Dadurch wird dieses Entropiefunktional physikalisch
relevant, da damit die thermodynamische Zustandsgröße Entropie
physikalisch sinnvoll definiert werden kann.
Gruß von Bruce |
|
 |
Karl-Heinz_M
Anmeldungsdatum: 18.09.2013
Beiträge: 2
Wohnort: Deggendorf
|
 Karl-Heinz_M Verfasst am: 17. Jan 2014 18:54 Titel: Entropie als Größe zur Systembeschreibung Karl-Heinz_M Verfasst am: 17. Jan 2014 18:54 Titel: Entropie als Größe zur Systembeschreibung |
 |
|
Entropie ist eine Größe, die sich relativ schwer bestimmen lässt, aber denoch notwendig ist, um jedes System zu beschrieben.
Die Entropie ist eine thermodynamische Größe, die ein System beschreibt (analog dem Durck). Die Größe Entropie ergibt sich aus dem zweiten Hauptsatz der Thermodynamik und gibt an, in welche Richtung ein "System läuft. (jeder kennt den Ausdruck: bei einer freiwillig ablaufenden Reaktion nimmt die Entropie zu). Die Entropie berechnet sich aus der Formel S = k ln(W) [k = Bolzmannkonstante, B = Besetzungszustand]. Durch diese Formel wird immer umgangssprachlich gesagt, die Entropie ist ein Maß für die Unordnung.
Beispiel: Ideales Kristallgitter, alle Atome befinden sich am gleichen Platz => W = 1 => S = k ln(1) = 0 (was auch sein sollte).
http://www.lernort-mint.de/Physikalische%20Chemie/Termodynamik/entropie.html |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8576
|
 jh8979 Verfasst am: 17. Jan 2014 18:57 Titel: jh8979 Verfasst am: 17. Jan 2014 18:57 Titel: |
 |
|
Gut dass das nach 9 Jahren noch gesagt wurde  |
|
 |
|
















 .
.