| Autor |
Nachricht |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18018
|
 TomS Verfasst am: 06. Aug 2018 14:35 Titel: FAQ - fundamentale Regeln der Quantenmechanik nach Everett TomS Verfasst am: 06. Aug 2018 14:35 Titel: FAQ - fundamentale Regeln der Quantenmechanik nach Everett |
 |
|
Ich möchte im Folgenden kurz modifizierte Regeln zur Quantenmechanik zusammenfassen, die zur 'Everettschen Formulierung' führen. Die Formulierung der Regeln ist mathematisch einfach gehalten, es existieren Verallgemeinerungen bzw. Präzisierungen ¹.
Kursiv gesetzter Text bezieht sich auf reale Systeme und deren Dynamik, Präparation und Messung, sowie tatsächlich messbare Größen d.h. Observablen sowie deren Messwerte.
Normal gesetzter Text bezieht sich auf rein mathematische Objekte, die die o.g. physikalischen Systeme etc. in gewissem Sinne repräsentieren ².
Die folgenden Regeln sind identisch (!) zu den etablierten Regeln ³ der 'orthodoxen Formulierung'
1. Die Beschreibung eines Quantensystems erfolgt im Rahmen eines separablen Hilbertraumes 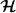
2. Der Zustand eines einzelnen ⁴ Quantensystems wird vollständig durch einen normierten Vektor ⁵ 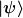 als Element dieses Hilbertraumes als Element dieses Hilbertraumes 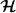 beschrieben. beschrieben.
3. Die Zeitentwicklung eines einzelnen isolierten ⁶ Quantensystems wird durch einen unitären Zeitentwicklungsoperator
 = e^{ -\mathrm{i}Ht })
mittels
\rangle = U(t)\,|\psi(0)\rangle)
beschrieben; 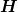 ist dabei der Hamiltonoperator. ist dabei der Hamiltonoperator.
Diese Regel ist vollständig äquivalent zur Schrödingergleichung ⁷
 \rangle = H \, |\psi(t) \rangle)
4. Eine beobachtbare Größe, d.h. eine Observable eines Quantensystems wird durch eine selbstadjungierten ⁸ Operator  repräsentiert, der auf die Zustandsvektoren repräsentiert, der auf die Zustandsvektoren 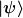 in in 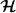 wirkt. wirkt.
--------------------
Die folgende Regel unterscheidet die 'Everettsche Formulierung' fundamental (!) von der sogenannten 'orthodoxen Interpretation':
EDIT: umformuliert
5. Unter der Messung einer Observable eines Quantensystems  versteht man zunächst eine spezielle Wechselwirkung dieses Quantensystems mit einem zweiten (makroskopischen) Quantensystem versteht man zunächst eine spezielle Wechselwirkung dieses Quantensystems mit einem zweiten (makroskopischen) Quantensystem  – dem sogenannten Messgerät – gemäß der o.g. unitären Zeitentwicklung. – dem sogenannten Messgerät – gemäß der o.g. unitären Zeitentwicklung.
Formal liegt eine Messung einer durch den Operator  repräsentierten Observablen dann vor, wenn ein beliebiger Gesamtzustand von Quantensystem und Messgerät repräsentierten Observablen dann vor, wenn ein beliebiger Gesamtzustand von Quantensystem und Messgerät

im Zuge der Wechselwirkung zu einer makroskopisch näherungsweise eindeutigen Korrelation  zwischen den Eigenzuständen zwischen den Eigenzuständen  des selbstadjungierten Operators des selbstadjungierten Operators  und den sogenannten Zeiger-Zuständen und den sogenannten Zeiger-Zuständen  des Messgerätes führt, so dass die Zeiger-Zustände die Messwerte der Observablen anzeigen. des Messgerätes führt, so dass die Zeiger-Zustände die Messwerte der Observablen anzeigen.
Phänomenologisch muss die im Zuge der Wechselwirkung entstehende Korrelation in der Form

dynamisch stabil bzw. robust sein, um als Messung gelten zu können ⁹.
--------------------
In der 'Everettschen Interpretation' stellen die folgenden Regeln ¹⁰ keine fundamentalen Axiome dar. Man kann stattdessen argumentieren, dass es möglich ist, sie aus dem Formalismus abzuleiten bzw. zumindest zu motivieren, und dass sie für praktische Anwendungsfälle weiterhin gültig sind. Zu diesbzgl. offenen Punkten s.u..
A. Die möglichen Messwerte einer Observable entsprechen dem Spektrum des korrespondierenden selbstadjungierten Operators  . .
B. Die Wahrscheinlichkeit, einen Messwert  zu erhalten, entspricht der Bornschen Regel zu erhalten, entspricht der Bornschen Regel
 = |\langle a | \psi\rangle|^2 )
C. Der Erwartungswert für die Messung von  , entspricht , entspricht
 \, a)
D. Aus Sicht eines Beobachters kann – im Falle aufeinanderfolgender Messungen am selben Quantensystemen – eine Messung mit Messwert  aufgefasst werden als Präparation des Gesamtsystems in einen neuen initialen Zustand repräsentiert durch den Zustandsvektor aufgefasst werden als Präparation des Gesamtsystems in einen neuen initialen Zustand repräsentiert durch den Zustandsvektor  , der in der Folge für die weitere Zeitentwicklung sowie weitere Messungen verwendet wird. Dies entspricht dem sogenannten von-Neumannsche Projektionspostulat, das aus Sicht eines Beobachters effektiv gültig bleibt. , der in der Folge für die weitere Zeitentwicklung sowie weitere Messungen verwendet wird. Dies entspricht dem sogenannten von-Neumannsche Projektionspostulat, das aus Sicht eines Beobachters effektiv gültig bleibt.
--------------------
¹ U.a. für entartete Unterräume, verallgemeinerte Messungen die nicht mittels Projektoren sondern positiver operatorwertiger Wahrscheinlichkeitsmaße (POVM) beschrieben werden, Darstellungen von Zuständen als Strahlen (Rays) bzw. in projektiven Hilberträumen, verallgemeinerte Zustände und Dichteoperatoren, kontinuierliche bzw. distributionswertige Basen, Gelfand Triples bzw. rigged Hilbert spaces. Für eine Einführung sind diese Details oft irrelevant – mit einer Ausnahme, nämlich den kontinuierlichen bzw. distributionswertige Basen für Orts- und Impulsraumdarstellung
² Die Bedeutung des Formalismus und der Repräsentation (ontisch, rein instrumentalistisch etc.) sowie die einzelnen Interpretationen der Quantenmechanik sind hier nicht Gegenstand. Allerdings dienen die Regeln als gemeinsamer Startpunkt für die wesentlichen Interpretationen, wobei diese je nach Interpretation teilweise angepasst werden.
³ Diese etablierten Regeln sind Gegenstand einiger Lehrbücher, z.B. Dirac, Cohen-Tannoudji, Sakurai, Weinberg, Griffiths, …
⁴ In statistischen bzw. Ensemble-Interpretationen wird dies dahingehend modifiziert, dass der Zustandsvektor nicht mehr ein einzelnes System repräsentiert, sondern lediglich ein Ensemble gleichartig präparierter Systeme. Dies spielt im Folgenden keine Rolle
⁵ Präziser ist die Formulierung der Repräsentation mittels einer Äquivalenzklasse  mit mit  und dem o.g. normierten Vektor und dem o.g. normierten Vektor 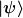 in in 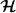 . .
Dies ist automatisch gegeben bei Verwendung projektorwertiger Zustände 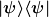 , insbs. bei der Betrachtung verallgemeinerter Zustände bzw. Dichteoperatoren. , insbs. bei der Betrachtung verallgemeinerter Zustände bzw. Dichteoperatoren.
⁶ Für nicht-isolierte Systeme wäre der Hamiltonoperator  ) zeitabhängig; dies spielt im Folgenden keine Rolle. zeitabhängig; dies spielt im Folgenden keine Rolle.
⁷ Diese Regel gilt im sogenannten Schrödinger-Bild. Es existieren andere, unitär-äquivalente Formulierungen, insbs. das Heisenberg- und das Wechselwirkungsbild, in denen die Zeitentwicklung vollständig oder teilweise von den Zustandsvektoren auf die Operatoren übertragen wird; letzteres spielt im Folgenden keine Rolle.
⁸ Ich bevorzuge die mathematische Bezeichnung ‚selbstadjungiert‘ und die klare Abgrenzung zu ‚symmetrisch‘; im endlich-dimensionalen Fall sind beide Bedeutungen identisch.
⁹ Ich habe der Übersichtlichkeit halber auf die Notation unbeobachteter Umgebungsfreiheitsgrade verzichtet; die Resultate zur Dekohärenz zeigen, dass diese Umgebungsfreiheitsgrade bei der Entstehung der o.g. Struktur des Zustandes eine maßgebliche Rolle spielen, d.h. diese Struktur wird nicht postuliert sondern kann auf Basis der Dekohärenz abgeleitet werden. Die o.g. Korrelation ist dabei lediglich makroskopisch näherungsweise eindeutig, es sind durchaus weitere Terme enthalten, oben angedeutet durch 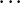 , die jedoch um viele Größenordnungen unterdrückt und daher phänomenologisch irrelevant sind. Darüberhinaus resultiert aus der Dekohärenz die dynamisch Stabilität bzw. Robustheit der o.g. Struktur unter weiterer Zeitentwicklung, d.h. phänomenologisch wird die Anzeige des Messgerätes nicht durch Interferenzen der mikroskopischen Freiheitsgrade zerstört, sondern bleibt makroskopisch beobachtbar. , die jedoch um viele Größenordnungen unterdrückt und daher phänomenologisch irrelevant sind. Darüberhinaus resultiert aus der Dekohärenz die dynamisch Stabilität bzw. Robustheit der o.g. Struktur unter weiterer Zeitentwicklung, d.h. phänomenologisch wird die Anzeige des Messgerätes nicht durch Interferenzen der mikroskopischen Freiheitsgrade zerstört, sondern bleibt makroskopisch beobachtbar.
¹⁰ Diese Regeln werden hier nur verkürzt dargestellt, da sie nicht Bestandteil des fundamentalen Axiomensystems sind.
--------------------
Ausgangspunkt der Überlegung ist das sogenannte Messproblems. Eine wesentliche Erkenntnis dazu ist das sogenannte Maudlin-Trilemma. Maudlin zeigt, dass die folgenden drei Aussagen zusammengenommen inkonsistent sind:
i) Der Zustandsvektor beschreibt das System gem. (2) vollständig
ii) Der Zustandsvektor folgt immer einer linearen Zeitentwicklung (3)
iii) Messungen haben immer ein definiertes Ergebnis (im Sinne einer definierten Eigenschaft bzgl. einer Observablen)
Die 'orthodoxe Interpretation' lehnt (ii) ab und postuliert ad hoc einen Kollaps.
Everett hält an (i - ii) fest und lehnt (iii), d.h. das Kollapspostulat, ab. Dies führt - wie wir sehen werden - dazu, dass im Widerspruch zu (iii) alle quantenmechanisch zulässigen Messergebnisse in je einer Komponente des Zustandsvektors repräsentiert werden. Diese Struktur folgt direkt aus (3).
Erläuterung zu wesentlichen Unterschieden zwischen 'Everettscher' sowie 'orthodoxer Interpretation':
Zunächst mal sind beide Formalismen mathematisch inäquivalent, weswegen man streng genommen von einer 'Everettschen Quantenmechanik' sprechen sollte.
In der 'orthodoxen Interpretation' nach von Neumann, Dirac u.a. wird der Begriff der Messung ohne konsistente Definition eingeführt. Die Forderung des Projektionspostulates im Zuge einer Messung führt zunächst zu einer logischen Inkonsistenz, denn einerseits widerspricht die Zeitentwicklung (die stochastische Projektion) im Zuge einer Messung der zuvor eingeführten unitären Zeitentwicklung, andererseits müsste das Messgerät als (makroskopisches) Quantensystem ebenfalls dieser unitären Zeitentwicklung gehorchen. Darüberhinaus resultiert aus der Unterscheidung zwischen gewöhnlichen quantenmechanischen Systemen einerseits sowie (makroskopischen) klassischen Messgeräten andererseits eine physikalisch völlig unbefriedigende Situation: der Quantenmechanik wird ein begrenzter Gültigkeitsbereich unterstellt, der nie eindeutig definiert werden konnte; einerseits soll sich das Messgerät im Zuge der Messung explizit klassisch = nicht-quantenmechanisch verhalten, andererseits wurde das Messgerät mittels Methoden konstruiert, die selbstverständlich auf quantenmechanischen Regeln beruhen. Insgs. bleibt nach dieser orthodoxen Argumentation offen, was ein Messgerät bzw. eine Messung von einem gewöhnlichen (makroskopischen) Quantensystem bzw. einer gewöhnlichen Wechselwirkung mit unitärer Zeitentwicklung unterscheidet. Demzufolge ist die 'orthodoxe Interpretation' unvollständig bzw. inkonsistent.
Everett verzichtet explizit auf das Projektionspostulat sowie die künstliche Unterscheidung zwischen Quantensystemen sowie klassischen Messgeräten; er behandelt Messungen als spezielle Klasse von Wechselwirkungen, und zwar dergestalt, dass eine dynamisch stabile / robuste Korrelation zwischen den Eigenschaften des zu messenden Quantensystems sowie dem (makroskopischen) jedoch ebenfalls quantenmechanisch zu beschreibenden Messgerät resultiert. Damit entspricht die Dynamik des Zustandsvektors vollständig und konsistent der unitären Zeitentwicklung. Daraus resultiert allerdings die Notwendigkeit, die Anwendbarkeit weiterer etablierter Regeln – die Everett im Zuge des Verzichts auf das Projektionspostulat eliminieren muss, die sich jedoch in Übereinstimmung mit phänomenologischen Beobachtungen befinden – zu motivieren oder zu beweisen. Darüberhinaus muss Everett auf die uns vertraute objektive Realität verzichten, derzufolge wir zumindest nach einer Messung einem bestimmten System eine konkrete, klassische Eigenschaft zuschreiben können; der Verzicht auf das Projektionspostulat bedeutet, dass man einem Quantensystem als Ganzes eine derartige Eigenschaft auf der fundamentalen Ebene nicht mehr zuschreiben darf, dass diese jedoch in Übereinstimmung mit unseren Experimenten beobachtbar wird.
Betrachten wir dazu ein Photon, das mit einer gewissen Wahrscheinlichkeit an einem halbdurchlässigen Spiegel reflektiert wird; nach Reflexion bzw. Transmission befindet sich das Photon in einem Superpositionszustand


wobei eine “1” bzw. eine “0” für ein bzw. kein Photon im jeweiligen Lichtweg steht.
Platzieren wir nun zwei Atome in die Lichtwege, d.h. je eines je Lichtweg, so wird jeweils ein Atom durch ein Photon geeigneter Energie in einen angeregten Zustand überführt. Die unitäre Zeitentwicklung liefert den Zustand
 \otimes |a,a\rangle \to |0,0\rangle \otimes (\alpha\,|a^\star,a\rangle + \beta\,| a,a^\star \rangle) )
Das Photon wird absorbiert, stattdessen erhalten wir einen verschränkten Zustand der beiden Atome; das Sternchen symbolisiert dabei den angeregten Zustand.
Der mathematische Formalismus sowie die Präparation derartiger Zustände ist seit Jahrzehnten etablierte Praxis; der anzuwendende Formalismus ist unstrittig.
Dies ändert sich bei Betrachtung der Messung bzw. Beobachtung!
Wir ersetzen die Atome durch ein makroskopisches System, bestehend aus zwei Detektoren mit Zeiger-Zuständen (P), einen Beobachter (O) sowie unbeobachtete Umgebungsfreiheitsgrade (nicht notiert). Die unitäre Zeitentwicklung liefert den Zustand
 \otimes |P,P\rangle \otimes |O_{ P,P } \rangle \to |0,0\rangle \otimes (\alpha\,|P^\star,P \rangle \otimes |O_{ P^\star,P } \rangle + \beta\,|P,P^\star \rangle \otimes |O_{ P,P^\star} \rangle) )
Der letzte Zustand widerspricht explizit unserer (klassisch geprägten) Alltagserfahrung: wir kennen keinen Beobachter, der sich in einem Superpositionszustand befindet, in dem er je einen Detektor im ersten bzw. zweiten Lichtweg mit bzw. ohne Anzeige einer Detektion UND einen Detektor im ersten bzw. zweiten Lichtweg ohne bzw. mit Anzeige einer Detektion sieht. Wir – als klassische Beobachter – sehen immer nur ENTWEDER einen Detektor im ersten bzw. zweiten Lichtweg mit bzw. ohne Anzeige einer Detektion ODETR einen Detektor im ersten bzw. zweiten Lichtweg ohne bzw. mit Anzeige einer Detektion.
Es gibt dazu letztlich zwei Auswege:
Die 'orthodoxe Interpretation' postuliert einen Kollaps, d.h. eine stochastische Reduktion dieses Superpositionszustandes auf eine der beiden Alternativen (der leere Photon-Zustand kann entfallen)

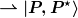
Die 'Everettsche Interpretation' akzeptiert die Existenz des Superpositionszustandes, der den Beobachter explizit einschließt
 )
Die zentrale Aussage von Everett et al. ist, dass der o.g. Kollaps ad hoc, offensichtlich unnötig sowie explizit inkonsistent ist. Es ist keine logische Begründung möglich, wann nun eine normale Wechselwirkung ohne Kollaps bzw. eine Messung mit Kollaps vorliegt. Insbs. kann kein Kriterium genannt werden, was diese Systeme und Experimente fundamental unterscheiden sollte. Aus diesen Gründen lehnen Everett et al. den Kollaps ab
Kurzer Ausblick zur Dekohärenz:
Inzwischen sind die Entstehung sowie die dynamischen Eigenschaften der Korrelationen zwischen Quantensystem bzw. dessen Zustand sowie Messgerät bzw. dessen Zeiger-Zuständen aufgrund der Dekohärenz mathematisch verstanden. Insbs. ist damit klar, warum die beiden 'Zweige'  und und  näherungsweise orthogonal bleiben, untereinander nicht mehr interferenzfähig sind – was man gemeinhin als 'wechselweise unbeobachtbar' bezeichnet – und warum diese Eigenschaften dynamisch stabil bzw. robust sind: Ursache ist letztlich die Verschränkung mit den Umgebungsfreiheitsgraden; isolierte Quantensysteme zeigen keine Dekohärenz und bleiben interferenzfähig. näherungsweise orthogonal bleiben, untereinander nicht mehr interferenzfähig sind – was man gemeinhin als 'wechselweise unbeobachtbar' bezeichnet – und warum diese Eigenschaften dynamisch stabil bzw. robust sind: Ursache ist letztlich die Verschränkung mit den Umgebungsfreiheitsgraden; isolierte Quantensysteme zeigen keine Dekohärenz und bleiben interferenzfähig.
Ausblick zur Bornschen Regel:
Eine allgemein akzeptierte Ableitung oder zumindest Motivation der Bornschen Regel auf Basis der Axiomen (1 - 5) sowie ggf. weiteren Annahmen ist der zentrale offene Punkt der 'Everettschen Quantenmechanik'.
Gleason's Theorem besagt, dass die in (B, C) genannten Formeln die einzige konsistente Möglichkeit darstellen, ein Wahrscheinlichkeitsmaß auf einem Hilbertraum einzuführen, d.h. Hilbertraumvektoren Wahrscheinlichkeiten zuzuordnen. D.h. dass wenn wir eine Wahrscheinlichkeit definieren wollen, z.B. weil wir statistische Häufigkeiten beobachten, dass dann das Wahrscheinlichkeitsmaß eindeutig festgelegt ist und dem in (B, C) entsprechen muss. Es ist jedoch keine allgemein akzeptierte Argumentation bekannt, die besagt, dass wenn wir die o.g. Axiome einführen, dass dann das o.g. Maß als Wahrscheinlichkeitsmaß interpretiert werden muss.
Wir können also den zweiten Schritt begründen, welches Wahrscheinlichkeitsmaß zu verwenden ist, unter der Annahme, dass wir überhaupt eines einführen wollen. Wir können jedoch nicht den ersten Schritt begründen, warum bei Vorliegen dieser zunächst rein deterministischen Theorie überhaupt Wahrscheinlichkeiten bzw. statistische Häufigkeiten für bestimmte - makroskopisch robuste - Zweige resultieren. Das Auftreten von Wahrscheinlichkeiten ist demnach keine Vorhersage der 'Everettschen Quantenmechanik' sondern muss (zunächst) als weiteres Postulat akzeptiert werden. Dies wird heute als wesentlicher offener Punkt angesehen; diesbzgl. vorliegende Argumentationen sind umstritten und gelten teilweise als zirkulär.
Zusammenfassung der wesentlichen Errungenschaften der 'Everettschen Formulierung:
- minimalistisches und konsistentes Axiomensystem ohne Kollaps
- keine Sonderstellung der Messung
- Berücksichtigung der Ergebnisse der Dekohärenz
- Indizien zur (teilweisen) Ableitbarkeit der Bornschen Regel (Gleason’s Theorem, Hartle-Frequency Operator)
Zusammenfassung der wesentlichen offenen Punkte der 'Everettschen Formulierung:
- Ansätze zur Ableitung der Bornschen Regel umstritten
- wenn ontologisch interpretiert, dann folgen die bekannten „Vielen Welten“
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
|
|















