| Autor |
Nachricht |
Hans-Dieter
Gast
|
 Hans-Dieter Verfasst am: 05. Jul 2017 20:32 Titel: Frage zu Wellen: Elektrodynamik / Quantenmechanik Hans-Dieter Verfasst am: 05. Jul 2017 20:32 Titel: Frage zu Wellen: Elektrodynamik / Quantenmechanik |
 |
|
Meine Frage:
Hallo, wir haben zur Prüfungsvorbereitung zwei Fragen, kann mir jemand damit bitte helfen?
Welche Frequenzen und Gesamtenergien können stehende elektromagnetische Wellen in einer quaderförmigen Vakuumkammer mit den Abmessungen l_x, l_y und l_z haben?
Warum gibt es bei stationären gebundenen Zuständen nur stehende Wellen und diskrete Energieeigenwerte?
Wenn E > V (x) gilt, so ist die Wellenfunktion in der Zeit und im Raum oszillierend. Wie hängen Frequenz und Wellenzahl von E ab und warum?
Meine Ideen:
Für die zweite Frage habe ich folgende Antwort gefunden, verstehe diese aber nicht:
Die Quantisierung der Energie folgt aus der Bedingung, dass die Wellenfunktion  x) überall beschränkt ist. x) überall beschränkt ist.
Zustande kommt dies, wenn zwei Umkehrpunkte existieren (Potentialtopf). Dann müssen die Wellenfunktionen stetig an die exponentiell abklingende Funktion anschließen. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 10. Jul 2017 21:29 Titel: index_razor Verfasst am: 10. Jul 2017 21:29 Titel: |
 |
|
| Hans-Dieter hat Folgendes geschrieben: | Meine Frage:
Warum gibt es bei stationären gebundenen Zuständen nur stehende Wellen und diskrete Energieeigenwerte?
[...]
Die Quantisierung der Energie folgt aus der Bedingung, dass die Wellenfunktion grübelndx) überall beschränkt ist.
|
"Überall beschränkt"? Das ist m.E. keine sinnvolle Bedingung an eine Wellenfunktion. Ein gebundener Zustand liegt vor, wenn die Aufenthaltswahrscheinlichkeitsdichte hinreichend schnell im Unendlichen abfällt. (Im allgemeinen schneller als  ) Mit diskreten Energiewerten hat das meines Wissens folgendes zu tun. ) Mit diskreten Energiewerten hat das meines Wissens folgendes zu tun.
Daß die Energie 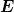 aus dem diskreten Spektrum des Hamiltonoperators stammt, bedeutet genau, daß ein Zustand aus dem diskreten Spektrum des Hamiltonoperators stammt, bedeutet genau, daß ein Zustand  existiert, so daß existiert, so daß
)
Ein solcher Zustand ist natürlich bezüglich der Eigendarstellung jeder (kontinuierlichen) Observable quadratintegrabel. Insbesondere gilt in der Ortsdarstellung
|^2\dd^3 x = \int\langle \psi|x\rangle\langle x|\psi\rangle \dd^3 x = \|\psi\|^2 = 1,)
wobei die Eigenschaft der verallgemeinerten Eigenzustände

benutzt wurde. Dies bedeutet aber eben, daß |^2) hinreichend schnell abfällt, sonst könnte das Integral links nicht gegen 1 konvergieren. hinreichend schnell abfällt, sonst könnte das Integral links nicht gegen 1 konvergieren.
Umgekehrt bedeutet es, wenn 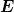 aus dem kontinuierlichen Spektrum stammt, daß ein Zustand wie in Gl. (1) eben gerade nicht existiert. Da H typischerweise aus Ableitungen und Multiplikation mit Funktionen von x besteht, existiert aber in der Ortsdarstellung trotzdem oft eine formale Lösung für (1), d.h. es existiert schon irgendeine entsprechende Funktion. Diese Funktion läßt sich aber nicht als Wahrscheinlichkeitsamplitude für den Ort interpretieren. Und somit läßt sich ihr auch kein quantenmechanischer Zustand zuordnen. Dieser Defekt äußert sich in der Ortsdarstellung dadurch, daß das Integral über die aus aus dem kontinuierlichen Spektrum stammt, daß ein Zustand wie in Gl. (1) eben gerade nicht existiert. Da H typischerweise aus Ableitungen und Multiplikation mit Funktionen von x besteht, existiert aber in der Ortsdarstellung trotzdem oft eine formale Lösung für (1), d.h. es existiert schon irgendeine entsprechende Funktion. Diese Funktion läßt sich aber nicht als Wahrscheinlichkeitsamplitude für den Ort interpretieren. Und somit läßt sich ihr auch kein quantenmechanischer Zustand zuordnen. Dieser Defekt äußert sich in der Ortsdarstellung dadurch, daß das Integral über die aus 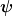 gebildete Aufenthaltswahrscheinlichkeitsdichte divergiert, weil die Funktion zu langsam abfällt. (Ansonsten könnte man das obige Argument umdrehen und wieder bei einem diskreten Energiewert landen.) gebildete Aufenthaltswahrscheinlichkeitsdichte divergiert, weil die Funktion zu langsam abfällt. (Ansonsten könnte man das obige Argument umdrehen und wieder bei einem diskreten Energiewert landen.)
Beispielsweise existieren für den freien Hamiltonian 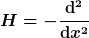 die "Eigenfunktionen" die "Eigenfunktionen" =\exp(\pm i\sqrt{E}x)) . Offensichtlich ist . Offensichtlich ist |^2 = 1) und das Integral über den gesamten Raum damit divergent. und das Integral über den gesamten Raum damit divergent.
(Edit: Latex repariert.)
Zuletzt bearbeitet von index_razor am 03. Nov 2018 09:51, insgesamt einmal bearbeitet |
|
 |
Hans-Dieter
Gast
|
 Hans-Dieter Verfasst am: 12. Jul 2017 22:00 Titel: Hans-Dieter Verfasst am: 12. Jul 2017 22:00 Titel: |
 |
|
Herzlichen Dank für die ausführliche Antwort. Mir ist die Sache noch nicht ganz klar. Dazu habe ich folgende Fragen:
Wie kommt man darauf, dass bei einem gebundenen Zustand die Aufenthaltswahrscheinlichkeitsdichte hinreichend schnell im Unendlichen abfällt? Ist das die Definition? Im Internet finde ich nämlich leider tausend andere Beschreibungen. Bei Wikipedia steht auch noch, dass ein solcher Zustand in einem Potential existieren kann, wenn es eine stehende Wellenfunktion gibt. Das war ja bei unserer Ausgangsfrage auch so, die Verbindung zu stehenden Wellen. Werden stehende Wellen durch solche Funktionen beschrieben, deren Betragsquadrat im Unendlichen gerade hinreichend schnell abfallen? Das kenne ich nämlich so nicht. Und eine weitere Frage: Woher weiß ich, dass wenn E aus dem diskreten Spektrum des Hamiltonoperators kommt, genau ein solcher Zustand existiert, der (1) erfüllt, also mit  ? Und umgekehrt, wenn E aus einem kontinuierlichen Spektrum kommt, solch ein Zustand gerade nicht existiert? ? Und umgekehrt, wenn E aus einem kontinuierlichen Spektrum kommt, solch ein Zustand gerade nicht existiert? |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18017
|
 TomS Verfasst am: 15. Jul 2017 08:33 Titel: TomS Verfasst am: 15. Jul 2017 08:33 Titel: |
 |
|
Gebundene, stationäre Zustände sind zunächst über ihre Energie in einem Potential definiert.
Z.B. ist die Referenzenergie im 1/r Potential gleich Null (für sehr große r verschwindet 1/r), und gebundene Zustände haben eine Energie kleiner Null. Für diese Zustände gilt außerdem, dass sie lokalisiert sind und bleiben, und dass ihre Wellenfunktion genügend schnell abfällt.
Nur die Wellenfunktion alleine zu betrachten ist m.E. nicht ausreichend. Die selben Wellenpakete wie oben können auch für ein freies Teilchen ohne Potential konstruiert werden, allerdings sind sie dann nicht stationär sondern zerfließen, es handelt sich nicht mehr um Eigenzustände, und ihre Energie (der Erwartungswrt) ist nicht mehr kleiner Null. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 15. Jul 2017 13:26 Titel: index_razor Verfasst am: 15. Jul 2017 13:26 Titel: |
 |
|
| Hans-Dieter hat Folgendes geschrieben: |
Wie kommt man darauf, dass bei einem gebundenen Zustand die Aufenthaltswahrscheinlichkeitsdichte hinreichend schnell im Unendlichen abfällt? Ist das die Definition?
|
Das muß ich korrigieren. Die Behauptung, die meine letzte Antwort suggeriert, Normierbarkeit hätte irgendwas mit dem Unterschied zwischen Bindungszustand und Nicht-Bindungszustand zu tun, ist natürlich Unsinn.
Ich fang nochmal an. Ich denke Bindungszustände kann man anschaulich dadurch charakterisieren, daß die Bewegung zu allen Zeiten auf ein endliches Raumgebiet beschränkt bleibt. Vermutlich ist es nicht ganz einfach das zu präzisieren. Man könnte damit anfangen zu fordern, daß die Ortsunschärfe endlich ist und konstant
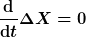
Ich weiß nicht, ob sich diese Bedingung zur Charakterisierung von Bindungszuständen eignet. Allerdings haben typische Bindungszustände diese Eigenschaft und zwar aus einem ganz einfachen Grund. Und hier kommen die Energieeigenzustände ins Spiel. Aus der Existenz von Zuständen, also letztlich normierbaren Funktionen, mit der Eigenschaft
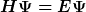
folgt sofort ihre triviale Zeitentwicklung
=e^{-iEt}\Psi(0))
Diese Zustände sind also zeitlich konstant, bis auf eine unwesentliche Phasenänderung. Hiermit kommen wir auf den Begriff der "stehenden Wellen". Denn bezüglich der der "Ortseigenbasis" können wir den Zustand zur Zeit t durch folgende Wellenfunktion darstellen
 = e^{-iEt}\psi(0,x),)
d.h. sie stellt eine harmonische Zeitänderung der Amplitude zwischen den räumlich fixen Punkten =0) dar. Insbesondere sind die Erwartungswerte aller explizit zeitunabhängigen Observablen konstant, also ist auch dar. Insbesondere sind die Erwartungswerte aller explizit zeitunabhängigen Observablen konstant, also ist auch
,(X^2 - \langle X\rangle^2)\Psi(t)\rangle)
zeitlich konstant. Sie erfüllen also die anfängliche Bedingung, mit der ich Bindungszustände charakterisieren wollte. Ich betone nochmal: diese Zeitunabhängigkeit ist die relevante Eigenschaft der Energieeigenzustände, nicht die Tatsache, daß sie normierbar sind. Sowohl die Existenz, d.h. Endlichkeit, der Unschärfe, also auch deren Zeitunabhängigkeit, gehen weit über die Folgerungen aus der Normierbarkeit hinaus. Die Bedingungen für das Verhalten im Unendlichen werden sogar noch verstärkt, denn nun muß sogar das Integral
|^2 x^2 \dd^3 x < \infty)
mit einem zusätzlichen Faktor 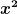 im Integranden existieren. Naiverweise würde man nun sogar erwarten, daß die Wahrscheinlichkeitsdichte schneller als im Integranden existieren. Naiverweise würde man nun sogar erwarten, daß die Wahrscheinlichkeitsdichte schneller als  abfällt. (Ich bin denke nicht, daß hieraus tatsächlich, abfällt. (Ich bin denke nicht, daß hieraus tatsächlich,  im Unendlichen folgt, denn L²-Funktionen sind gegen solche Argumente widerspenstiger als stetige Funktionen. Es folgt wohl allgemein, daß sich das Teilchen immer seltener und seltener außerhalb immer größer werdender beschränkter Raumgebiete aufhält.) im Unendlichen folgt, denn L²-Funktionen sind gegen solche Argumente widerspenstiger als stetige Funktionen. Es folgt wohl allgemein, daß sich das Teilchen immer seltener und seltener außerhalb immer größer werdender beschränkter Raumgebiete aufhält.)
Nun gibt es natürlich auch normierbare Zustände, die zu Elementen des kontinuierlichen Spektrums gehören, nämlich kontinuierliche Überlagerungen von "Energieeigenzuständen", d.h. du kannst auch jeder normierten Funktion ) auf dem kontinuierlichen Energie-Spektrum einen Zustand auf dem kontinuierlichen Energie-Spektrum einen Zustand 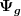 zuordnen, mit zuordnen, mit
|^2\dd E = \|\Psi_g\|^2 = 1.)
(Formal schreibt man dafür \ |E\rangle ) .) .)
Diese Zustände müssen aber nicht lokalisiert sein und wenn sie es sind, bleiben sie es im allgemeinen nicht, d.h.  im Laufe der Zeit. (Darauf hat ja inzwischen auch TomS hingewiesen.) im Laufe der Zeit. (Darauf hat ja inzwischen auch TomS hingewiesen.)
| Zitat: | Und eine weitere Frage: Woher weiß ich, dass wenn E aus dem diskreten Spektrum des Hamiltonoperators kommt, genau ein solcher Zustand existiert, der (1) erfüllt, also mit  ? ?
Und umgekehrt, wenn E aus einem kontinuierlichen Spektrum kommt, solch ein Zustand gerade nicht existiert?
|
Das ist im wesentlichen die Definition des reinen Punktspektrums von H. Es handelt sich dabei um nichts anderes als die Eigenwerte des Operators. Es muß nicht genau ein solcher Vektor existieren, aber mindestens einer muß existieren und zwar nicht der Nullvektor. Und wenn ein  existiert, der die Gleichung erfüllt, dann existiert auch ein auf eins normierter mit derselben Eigenschaft. existiert, der die Gleichung erfüllt, dann existiert auch ein auf eins normierter mit derselben Eigenschaft. |
|
 |
|
|
















 x) überall beschränkt ist.
x) überall beschränkt ist.