| Autor |
Nachricht |
Mr Maths
Anmeldungsdatum: 15.05.2011
Beiträge: 110
|
 Mr Maths Verfasst am: 29. Apr 2017 14:45 Titel: Paritätsoperator (unitär, hermitesch, Eigenwerte) Mr Maths Verfasst am: 29. Apr 2017 14:45 Titel: Paritätsoperator (unitär, hermitesch, Eigenwerte) |
 |
|
Hi.
Der Paritätsoperator ist ja folgendermaßen definiert:  wobei wobei  gilt. gilt.
(Betrachtet bei einem Teilchen mit Masse m und einem Freiheitsgrad)
Ich habe gezeigt, dass der Paritätsoperator linear und invertierbar ist:
Linearität:
 und offentsichtlich gilt auch und offentsichtlich gilt auch  = \hat{P}|x\rangle +\hat{P}|y\rangle) , da einfach statt dem x und y ein -x und -y gemacht wird. , da einfach statt dem x und y ein -x und -y gemacht wird.
Invertierbarkeit:
 . Also gilt auch . Also gilt auch 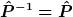 . .
Aufgrund der obigen erfüllten Bedingungen handelt es sich nun um einen unitären Operator. Und bei unitären Operator haben die Eigenwerte immer Betrag 1, also -1 bzw. +1.
Laut Eigenwertgleichung gilt folgendes:
 , also könnte hier a entweder -1 oder +1 sein, aber ich bin mir nicht ganz sicher warum das so ist. , also könnte hier a entweder -1 oder +1 sein, aber ich bin mir nicht ganz sicher warum das so ist.
Folgendes kann ich noch sagen:
 und und 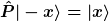 . Doch leider gilt ja . Doch leider gilt ja  und somit gilt das nicht, um zu beweisen, dass die Eigenweärte +-1 sind. und somit gilt das nicht, um zu beweisen, dass die Eigenweärte +-1 sind.
Würde mich über einen Denkanstoss freuen, sodass ich alleine draufkommen kann.
MfG
Mr Maths
|
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 29. Apr 2017 16:56 Titel: Re: Paritätsoperator (unitär, hermitesch, Eigenwerte) index_razor Verfasst am: 29. Apr 2017 16:56 Titel: Re: Paritätsoperator (unitär, hermitesch, Eigenwerte) |
 |
|
| Mr Maths hat Folgendes geschrieben: | Hi.
Der Paritätsoperator ist ja folgendermaßen definiert:  wobei wobei  gilt. gilt.
(Betrachtet bei einem Teilchen mit Masse m und einem Freiheitsgrad)
Ich habe gezeigt, dass der Paritätsoperator linear und invertierbar ist:
Linearität:
 und offentsichtlich gilt auch und offentsichtlich gilt auch  = \hat{P}|x\rangle +\hat{P}|y\rangle) , da einfach statt dem x und y ein -x und -y gemacht wird. , da einfach statt dem x und y ein -x und -y gemacht wird.
|
Hier wird m.E. der Gedankengang nicht klar. Ich denke die Dirac-Notation ist für diese Aufgabe nicht wirklich geeignet. Ich würde mich auf die reine Ortsdarstellung konzentrieren, also ) betrachten und mit der Definition betrachten und mit der Definition
(x) = f(-x))
arbeiten. (Ich behaupte mal, daß diese Definition in  "fast überall Sinn ergibt" ohne genauer darüber nachzudenken, was das eigentlich bedeutet.) Was du dann zeigen mußt, ist "fast überall Sinn ergibt" ohne genauer darüber nachzudenken, was das eigentlich bedeutet.) Was du dann zeigen mußt, ist
(x) = \lambda (Pf)(x) + (Pg)(x),)
d.h. die Funktion 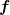 wird mit wird mit  multipliziert, nicht das Argument x, wie deine erste Gl. auszusagen scheint. Auch bei dem Beweis der Additivität kannst du dann etwas expliziter sein, als einfach zu behaupten es sei offensichtlich. multipliziert, nicht das Argument x, wie deine erste Gl. auszusagen scheint. Auch bei dem Beweis der Additivität kannst du dann etwas expliziter sein, als einfach zu behaupten es sei offensichtlich.
| Zitat: |
Invertierbarkeit:
 . Also gilt auch . Also gilt auch 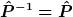 . .
Aufgrund der obigen erfüllten Bedingungen handelt es sich nun um einen unitären Operator. Und bei unitären Operator haben die Eigenwerte immer Betrag 1, also -1 bzw. +1.
|
Vorsicht. Es handelt sich um einen unitären und selbstadjungierten Operator. Die Eigenwerte eines unitären Operators liegen auf dem komplexen Einheitskreis  . Die eines selbstadjungierten Operators auf der reellen Achse . Die eines selbstadjungierten Operators auf der reellen Achse 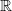 . Erst aus der Kombination beider Eigenschaften folgt, daß P höchstens die Eigenwerte . Erst aus der Kombination beider Eigenschaften folgt, daß P höchstens die Eigenwerte  haben kann, welches genau die Schnittmenge haben kann, welches genau die Schnittmenge  ist. ist.
| Zitat: |
Laut Eigenwertgleichung gilt folgendes:
 , also könnte hier a entweder -1 oder +1 sein, aber ich bin mir nicht ganz sicher warum das so ist. , also könnte hier a entweder -1 oder +1 sein, aber ich bin mir nicht ganz sicher warum das so ist.
Folgendes kann ich noch sagen:
 und und 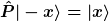 . Doch leider gilt ja . Doch leider gilt ja  und somit gilt das nicht, um zu beweisen, dass die Eigenweärte +-1 sind. und somit gilt das nicht, um zu beweisen, dass die Eigenweärte +-1 sind.
|
Vergiß die Dirac-Notation. Was soll  sein? Es handelt sich um irgendeine Funktion sein? Es handelt sich um irgendeine Funktion ) . Natürlich gilt nicht für jede Funktion . Natürlich gilt nicht für jede Funktion =f(-x)) . Aber für einige schon. Und um genau die geht es. . Aber für einige schon. Und um genau die geht es.
|
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 29. Apr 2017 17:20 Titel: Re: Paritätsoperator (unitär, hermitesch, Eigenwerte) index_razor Verfasst am: 29. Apr 2017 17:20 Titel: Re: Paritätsoperator (unitär, hermitesch, Eigenwerte) |
 |
|
| index_razor hat Folgendes geschrieben: | Ich würde mich auf die reine Ortsdarstellung konzentrieren, also ) betrachten und mit der Definition betrachten und mit der Definition
(x) = f(-x))
arbeiten. (Ich behaupte mal, daß diese Definition in  "fast überall Sinn ergibt" ohne genauer darüber nachzudenken, was das eigentlich bedeutet.) "fast überall Sinn ergibt" ohne genauer darüber nachzudenken, was das eigentlich bedeutet.)
|
P.S. Was es bedeutet, ist, glaube ich, folgendes: Es gibt eine dichte Teilmenge von stetigen Funktionen in ) , auf welcher die obige Definition sinnvoll ist und einen beschränkten Operator ergibt. Die eindeutige stetige Fortsetzung dieses Operators auf den Abschluß seines Definitionsbereichs ist der fragliche Operator auf , auf welcher die obige Definition sinnvoll ist und einen beschränkten Operator ergibt. Die eindeutige stetige Fortsetzung dieses Operators auf den Abschluß seines Definitionsbereichs ist der fragliche Operator auf ) . .
|
|
 |
Mr Maths
Anmeldungsdatum: 15.05.2011
Beiträge: 110
|
 Mr Maths Verfasst am: 29. Apr 2017 18:49 Titel: Mr Maths Verfasst am: 29. Apr 2017 18:49 Titel: |
 |
|
Hallo,
danke für die schnelle Antwort. Ich verstehe was du meinst. Ich habe jetzt die originale Aufgabe hochgeladen.  ist doch einfach der mathematisch beschriebende Zustand eines Teilchens mit einem Freiheitsgrad x und dieser beschriebene Zustand kann z.B. eine Wellenfunktion ist doch einfach der mathematisch beschriebende Zustand eines Teilchens mit einem Freiheitsgrad x und dieser beschriebene Zustand kann z.B. eine Wellenfunktion ) sein. Also müsste es egal sein, ob ich es mit Funktionen oder Zuständen in Dirac-Schreibweise beweise, denke ich. sein. Also müsste es egal sein, ob ich es mit Funktionen oder Zuständen in Dirac-Schreibweise beweise, denke ich.
Ich versuchs nochmal:
Linearität:
Sei =\lambda\psi_1(x)+\psi_2(x)\Rightarrow \hat{P}(\lambda\psi_1(x)+\psi_2(x))=\hat{P}\psi_3(x)=\psi_3(-x)=\lambda\psi_1(-x)+\psi_2(-x) = \lambda\hat{P}\psi_1(x)+\hat{P}\psi_2(x))
Der P-Operator hat auf die Konstante ja keine Wirkung, da die Konstante  nicht vom Freiheitsgrad x abhängig ist. nicht vom Freiheitsgrad x abhängig ist.
(Okay, irgendwie macht es mehr Sinn, wenn man mit Funktionen arbeitet, denn sonst könnte obiges gar nicht gut beweisen wirklich, keine Ahung warum auf der Aufgabe das anders aufgeschrieben wurde.)
Dann gilt für die Eigenzustände:
Für ungerade Funktionen 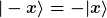 ist der EW=-1 und für gerade Funktionen ist der EW=-1 und für gerade Funktionen 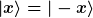 ist der EW=1. Okay, das habe ich jetzt verstanden. ist der EW=1. Okay, das habe ich jetzt verstanden.
Aber beim Beweis, dass P hermitesch sein soll, komme ich nicht wirklich weiter. Laut Definition muss  = [\langle \psi_2|(\hat{P}^\dag|\psi_1\rangle)]^*) gelten. Wobei gelten. Wobei  gelten muss. Aber da dieser Operator Linear und Invertierbar ist, d.h. unitär, gilt das schonmal. gelten muss. Aber da dieser Operator Linear und Invertierbar ist, d.h. unitär, gilt das schonmal.
Dann muss noch gelten, dass P ein symmetrischer Operator sein muss:

Ausgerechnet wär das dann ja: , \psi_1(x)\rangle=\langle \psi_2(x), \psi_1(-x)\rangle)
Aber genau das gilt ja nur, wenn beide Funktionen 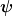 gerade sind, ansonsten würden das ja nicht klappen. Ist das so richtig? gerade sind, ansonsten würden das ja nicht klappen. Ist das so richtig?
Grüße
Mr Maths
| Beschreibung: |
|
| Dateigröße: |
41.01 KB |
| Angeschaut: |
9705 mal |

|
|
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18026
|
 TomS Verfasst am: 29. Apr 2017 19:20 Titel: TomS Verfasst am: 29. Apr 2017 19:20 Titel: |
 |
|
Der Zustand |x> beschreibt einen Ortseigenzustand. Ein allgemeiner Zustand wäre |psi>. Und die Wellenfunktion in diesem Zustand lautet
 = \langle x|\psi\rangle)
Die Wirkung des Paritätsoperators in der darstellungsfreien Dirac-Notation überträgt sich dann auf die Wellenfunktion wie folgt:
 = \langle x|P|\psi\rangle)
|
|
 |
Mr Maths
Anmeldungsdatum: 15.05.2011
Beiträge: 110
|
 Mr Maths Verfasst am: 29. Apr 2017 20:14 Titel: Mr Maths Verfasst am: 29. Apr 2017 20:14 Titel: |
 |
|
Verstehe danke dir für die Antwort, dann versuch ich alles nochmal mit der Definition in der Aufgabe zu beweisen: 
Für Linearität: =P(|x\rangle(1+\lambda))=\lambda|-x\rangle + |-x\rangle = \lambda P|x\rangle + P|x\rangle)
Invertierbarkeit:
 . Also gilt auch . Also gilt auch 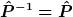 . .
Hermitesch: ^*)
Ist das so gemeint, wenn man den P-Operator mit Hilfe von Ortseigenzustände definiert?
|
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 30. Apr 2017 09:19 Titel: index_razor Verfasst am: 30. Apr 2017 09:19 Titel: |
 |
|
| Mr Maths hat Folgendes geschrieben: |
Aber beim Beweis, dass P hermitesch sein soll, komme ich nicht wirklich weiter. Laut Definition muss  = [\langle \psi_2|(\hat{P}^\dag|\psi_1\rangle)]^*) gelten. Wobei gelten. Wobei  gelten muss. Aber da dieser Operator Linear und Invertierbar ist, d.h. unitär, gilt das schonmal. gelten muss. Aber da dieser Operator Linear und Invertierbar ist, d.h. unitär, gilt das schonmal.
Dann muss noch gelten, dass P ein symmetrischer Operator sein muss:

Ausgerechnet wär das dann ja: , \psi_1(x)\rangle=\langle \psi_2(x), \psi_1(-x)\rangle)
Aber genau das gilt ja nur, wenn beide Funktionen 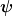 gerade sind, ansonsten würden das ja nicht klappen. Ist das so richtig? gerade sind, ansonsten würden das ja nicht klappen. Ist das so richtig?
|
Doch das klappt schon. Aus deiner Beschreibung schließe ich, daß ihr den Begriff "hermitesch" als synonym für "selbstadjungiert" verwendet.
Die Selbstadjungiertheit folgt aus der Symmetrie und der Beschränktheit des Operators. Die Symmetrie ist leicht mit dem  -Produkt zu zeigen. Der wesentliche Schritt hierbei ist -Produkt zu zeigen. Der wesentliche Schritt hierbei ist
f(-x)\dd x = \int \bar g(-x)f(x)\dd x = ...)
Warum gilt das? Der Rest ist nur noch Einsetzen von Definitionen.
|
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 30. Apr 2017 10:09 Titel: index_razor Verfasst am: 30. Apr 2017 10:09 Titel: |
 |
|
| Mr Maths hat Folgendes geschrieben: |
Für Linearität: =P(|x\rangle(1+\lambda))=\lambda|-x\rangle + |-x\rangle = \lambda P|x\rangle + P|x\rangle)
|
Du schreibst nur Gleichungen hintereinander, beweist aber nichts.
Linearität bedeutet, daß für alle Vektoren  und Zahlen und Zahlen  die Gleichung die Gleichung
=Pf + \lambda P g)
gilt. Wie du das mit Hilfe der gegebenen "Definition" von P beweisen solltest, ist mir ehrlich gesagt etwas schleierhaft. Aber zum Glück steht davon in der Aufgabe ja auch nichts. Vielleicht sollst du das einfach voraussetzen.
| Zitat: |
Invertierbarkeit:
 . Also gilt auch . Also gilt auch 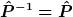 . .
|
Das zeigt zunächst, daß " " ein Fixpunkt von " ein Fixpunkt von 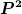 ist. Für die Invertierbarkeit brauchst du noch ein bißchen mehr. ist. Für die Invertierbarkeit brauchst du noch ein bißchen mehr.
| Zitat: |
Hermitesch: ^*)
Ist das so gemeint, wenn man den P-Operator mit Hilfe von Ortseigenzustände definiert? |
Wenn man "Ortseigenzustände" einführt, ergibt  im allgemeinen nicht mal Sinn, weil Ortseigenzustände nicht aus einem Hilbertraum stammen. Warum die Aufgabenstellung solche Ungetüme ins Feld führt, verstehe ich nicht. im allgemeinen nicht mal Sinn, weil Ortseigenzustände nicht aus einem Hilbertraum stammen. Warum die Aufgabenstellung solche Ungetüme ins Feld führt, verstehe ich nicht.
Im übrigen ist die Dirac-Notation  auf eine Weise mehrdeutig, die äußerst fatal sein kann, wenn die Selbstadjungiertheit des betrachteten Operators P noch in Frage steht. In diesem Fall mußt du auf eine Weise mehrdeutig, die äußerst fatal sein kann, wenn die Selbstadjungiertheit des betrachteten Operators P noch in Frage steht. In diesem Fall mußt du 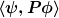 und und  strikt unterscheiden. strikt unterscheiden.
|
|
 |
Mr Maths
Anmeldungsdatum: 15.05.2011
Beiträge: 110
|
 Mr Maths Verfasst am: 30. Apr 2017 16:31 Titel: Mr Maths Verfasst am: 30. Apr 2017 16:31 Titel: |
 |
|
Hallo,
danke für die Antworten. Ich dachte, dass die Aufgabe das Beweisen für diesen konkreten Fall verlangt, also 1 Freiheitsgrad x und jetzt nicht im mehrdimensionalen.
Zum Zeigen der Hermitizität:
Ich bin mir nicht ganz sicher, wie ich von folgendem aus weiter vorgehen könnte: f(-x)\dd%20x%20=%20\int%20\bar%20g(-x)f(x)\dd%20x%20%20)
Für mich ergibt es nur Sinn, falls es sich um symmetrische Funktionen handelt. Laut Wikipedia ist ein Operator erst dann hermitisch, wenn dieser Symmetrisch ist und das soll man ja genau zeigen mit der obigen Gleichung. Aber ich weiß nicht, mit welcher Definition ich die Funktionen ersetzen soll.
Kannst du mir da bitte einen Tipp geben, worauf ich achten soll.
|
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 30. Apr 2017 16:56 Titel: index_razor Verfasst am: 30. Apr 2017 16:56 Titel: |
 |
|
| Mr Maths hat Folgendes geschrieben: | Hallo,
danke für die Antworten. Ich dachte, dass die Aufgabe das Beweisen für diesen konkreten Fall verlangt, also 1 Freiheitsgrad x und jetzt nicht im mehrdimensionalen.
|
Ja, das steht so in der Aufgabe. Ob ein, drei oder n Dimensionen macht aber keinen großen Unterschied. Worauf willst du hinaus?
| Zitat: |
Zum Zeigen der Hermitizität:
Ich bin mir nicht ganz sicher, wie ich von folgendem aus weiter vorgehen könnte: f(-x)\dd%20x%20=%20\int%20\bar%20g(-x)f(x)\dd%20x%20%20)
Für mich ergibt es nur Sinn, falls es sich um symmetrische Funktionen handelt. Laut Wikipedia ist ein Operator erst dann hermitisch, wenn dieser Symmetrisch ist und das soll man ja genau zeigen mit der obigen Gleichung. Aber ich weiß nicht, mit welcher Definition ich die Funktionen ersetzen soll.
|
Das Hilbertraumprodukt im  ist doch ist doch
f(x)\dd x)
Dann gilt also
(Pf)(x)\dd x = \int \bar g(x)f(-x)\dd x = ... ?)
Jetzt mußt du irgendwie die Wirkung von P auf g rüberschaufeln, so daß am Ende da (x)}) steht. Den nächsten Schritt habe ich dir schon genannt. Du mußt dir noch eine Rechtfertigung für ihn einfallen lassen, mit dem er für alle f, g gilt. ( Stichwort: Integraltransformationssatz) steht. Den nächsten Schritt habe ich dir schon genannt. Du mußt dir noch eine Rechtfertigung für ihn einfallen lassen, mit dem er für alle f, g gilt. ( Stichwort: Integraltransformationssatz)
|
|
 |
|
|
















