| Autor |
Nachricht |
SimonPhysik
Anmeldungsdatum: 08.11.2016
Beiträge: 72
|
 SimonPhysik Verfasst am: 08. Nov 2016 23:18 Titel: Rotierende Masse SimonPhysik Verfasst am: 08. Nov 2016 23:18 Titel: Rotierende Masse |
 |
|
Eine Masse (idealisiert punktförmig) von 30 kg
sei am Ende eines starren Balkens befestigt.
Das andere Ende des Balkens ist in einem Lager angebracht, so dass der Balken in der horizontalen Ebene um die vertikale
Achse rotieren kann. Vereinfacht sei die Masse des Balkens
als vernachlässigbar klein angenommen. Der Balken hat eine Länge von 1.5 m
a) Die Winkelgeschwindigkeit omega(t) des Balkens mit Masse wird durch eine Vorrichtung gleichmässig mit einer Rate von 10 Grad pro sec^2 beschleunigt. Berechnen Sie das Drehmoment der Bahnkurve der Masse bezogen auf den Lagerpunkt des Balkens.
Meine Ideen:
Ich habe die Winkelbeschleunigung gegeben und brauche das Drehmoment. Das kann man mit m * r^2 * Winkelbeschleunigung berchnen. Das wäre dann
M = 30 kg * 1,5 m ^2 * 10 s^(-2) = 675 Nm
Ist das so korrekt? |
|
 |
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5852
|
 Myon Verfasst am: 09. Nov 2016 00:30 Titel: Myon Verfasst am: 09. Nov 2016 00:30 Titel: |
 |
|
Hallo Simon!
Aus meiner Sicht ist das korrekt so, nur dass Du die Winkelbeschleunigung in Rad pro s^2 umrechnen musst, was zu einem anderen Ergebnis führt. |
|
 |
SimonPhysik
Anmeldungsdatum: 08.11.2016
Beiträge: 72
|
 SimonPhysik Verfasst am: 09. Nov 2016 00:54 Titel: SimonPhysik Verfasst am: 09. Nov 2016 00:54 Titel: |
 |
|
Ok danke. Kurz eine Frage noch. Was ist mit der Bahnkurve der Drehmomente genau gemeint??
10 grad wären doch 10 pi / 180 rad
Damit dann M = 11.8 N m ??
Leider gibt es noch zwei Teilaufgaben dazu, wo ich etwas hänge
b) Der Balken rotiere anfangs mit einer konstanten Winkelgeschwindigkeit von 60 grad pro Sekunde. Der Masse wird zur Zeit t_0 ein Hindernis entgegengestellt, so dass die Drehbe-
wegung innerhalb von 1/100 sec
gestoppt wird. Berechnen Sie das Drehmoment der
Bahnkurve der Masse (bezogen auf den Lagerpunkt des Balkens).
Kannst du mir da einen Tipp für den Ansatz geben? |
|
 |
SimonPhysik
Anmeldungsdatum: 08.11.2016
Beiträge: 72
|
 SimonPhysik Verfasst am: 09. Nov 2016 09:17 Titel: SimonPhysik Verfasst am: 09. Nov 2016 09:17 Titel: |
 |
|
Oder geht es so ;
Winkelbeschleunigung = Winkelgeschwindigkeit / t_0
Und dann daraus M= r^2 m * Winkelgeschwindigkeit / t_0
Ist das so ok?
Was ist mit Bahnkurve egtl gemeint genau? |
|
 |
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5852
|
 Myon Verfasst am: 09. Nov 2016 11:30 Titel: Myon Verfasst am: 09. Nov 2016 11:30 Titel: |
 |
|
Ja, die Rechnung ist OK (wobei natürlich durch die 1/100 Sekunde geteilt wird).
Die Formulierung "Drehmoment der Bahnkurve der Masse" finde ich etwas seltsam; jeder Körper hat bezüglich eines betrachteten Punktes oder einer Achse einen Drehimpuls. Ändert dieser, so muss auf den Körper (wieder bezogen auf den Punkt oder die Achse) ein Drehmoment wirken. Dieses ist vermutlich hier gefragt. |
|
 |
SimonPhysik
Anmeldungsdatum: 08.11.2016
Beiträge: 72
|
 SimonPhysik Verfasst am: 09. Nov 2016 11:54 Titel: SimonPhysik Verfasst am: 09. Nov 2016 11:54 Titel: |
 |
|
Danke. Jetzt kommt egtl meine Problem Teilaufgabe:
c)
Zusätzlich zu der Masse am Ende des Balkens sei eine weitere (idealisiert punktförmige) Masse von 40 kg an dem Balken angebracht, in einem Abstand von 0,5 m vom Lagerpunkt. Der Balken rotiere anfangs mit einer konstanten Winkelgeschwindigkeit von 60 Grad pro Sekunde. Dem Balken wird zur Zeit
t_0 ein Hindernis entgegengestellt, das den
Balken in einem Abstand r_0 vom Lagerpunkt trifft und die Drehbewegung innerhalb
von1 / 100 sec stoppt. Wie muss r_0 gewählt werden, damit die Belastung des Lagers möglichst gering ist?
Ich weis nicht wie ich das machen soll?
Wahrscheinlich muss ich irgendwas ableiten. Kannst du mir den Ansatz sagen? |
|
 |
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5852
|
 Myon Verfasst am: 09. Nov 2016 12:39 Titel: Myon Verfasst am: 09. Nov 2016 12:39 Titel: |
 |
|
|
Durch das Hindernis bei r_0 werden die beiden Massen in kurzer Zeit abgebremst. Tipp: Betrachte das auf die beiden Massen wirkende Drehmoment bezüglich des Punktes r_0. Wenn dieses verschwindet, wirkt auf das Lager keine Kraft. |
|
 |
SimonPhysik
Anmeldungsdatum: 08.11.2016
Beiträge: 72
|
 SimonPhysik Verfasst am: 09. Nov 2016 12:46 Titel: SimonPhysik Verfasst am: 09. Nov 2016 12:46 Titel: |
 |
|
Muss ich dann ein Gleichungsystem aufstellen
Einmal mit M = (1,5m - r_0)^2 *m * alpha=0
M= )0,5 + r_0)^2* m * alpha =0
so? |
|
 |
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5852
|
 Myon Verfasst am: 09. Nov 2016 13:06 Titel: Myon Verfasst am: 09. Nov 2016 13:06 Titel: |
 |
|
|
Nein. Es sollte ja schon intuitiv klar sein, dass das Hindernis zwischen den beiden Massen liegen muss. Die beiden Drehmomente bezüglich r_0 haben also verschiedene Vorzeichen. Du kannst die Summe der beiden Drehmomente bilden und gleich null setzen. |
|
 |
SimonPhysik
Anmeldungsdatum: 08.11.2016
Beiträge: 72
|
 SimonPhysik Verfasst am: 09. Nov 2016 13:32 Titel: SimonPhysik Verfasst am: 09. Nov 2016 13:32 Titel: |
 |
|
|
wie bringe ich dann die 0,5 m und die 1,5 m mit rein? |
|
 |
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5852
|
 Myon Verfasst am: 09. Nov 2016 13:51 Titel: Myon Verfasst am: 09. Nov 2016 13:51 Titel: |
 |
|
Die beiden Massen werden abgebremst. Es wirken auf sie also Kräfte F1, F2, die Du durch gegebene Grössen ausdrücken kannst. Damit das Drehmoment bezüglich r_0 verschwindet, muss gelten
=F_2(r_0-0.5\,\mathrm{m})) . . |
|
 |
SimonPhysik
Anmeldungsdatum: 08.11.2016
Beiträge: 72
|
 SimonPhysik Verfasst am: 09. Nov 2016 21:29 Titel: SimonPhysik Verfasst am: 09. Nov 2016 21:29 Titel: |
 |
|
Auf welches Ergebnis kommst du denn dabei : Bei mir kommt immer etwas falsches raus?
Man muss ja folgenden Gleichung umstellen:
30 kg * ( 1,5m - r_0 )^2 = 40 kg * (r_0 - 0,5 m)^2 |
|
 |
SimonPhysik
Anmeldungsdatum: 08.11.2016
Beiträge: 72
|
 SimonPhysik Verfasst am: 09. Nov 2016 21:32 Titel: SimonPhysik Verfasst am: 09. Nov 2016 21:32 Titel: |
 |
|
|
Ich komme auf 0,96 m |
|
 |
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5852
|
 Myon Verfasst am: 09. Nov 2016 23:21 Titel: Myon Verfasst am: 09. Nov 2016 23:21 Titel: |
 |
|
Bei mir sieht die Gleichung etwas anders aus.
Auf die Masse  wirkt während der Abbremszeit die Kraft wirkt während der Abbremszeit die Kraft
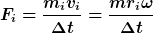
Dies führt zur Gleichung
=\frac{m_2r_2\omega}{\Delta t}(r_0-r_2))
Diese lässt sich leicht nach 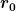 umformen. Ich erhalte etwa 1.19m - was auf den ersten Blick vielleicht noch erstaunlich ist, da die äussere Masse ja die leichtere ist. Allerdings hat sie auch die dreifache Geschwindigkeit, wodurch eine höhere Kraft auf sie wirkt beim Abbremsen. umformen. Ich erhalte etwa 1.19m - was auf den ersten Blick vielleicht noch erstaunlich ist, da die äussere Masse ja die leichtere ist. Allerdings hat sie auch die dreifache Geschwindigkeit, wodurch eine höhere Kraft auf sie wirkt beim Abbremsen.
Ich kann für die Richtigkeit dieser Lösung nicht garantieren bzw. ob die Aufgabe so gemeint ist, aber in meinen Augen sollte es so stimmen. |
|
 |
lh
Gast
|
 lh Verfasst am: 10. Nov 2016 07:33 Titel: lh Verfasst am: 10. Nov 2016 07:33 Titel: |
 |
|
Ich glaube,dass man bei c anders rechnen muss
und zwar so dass das Drehmoment im Lager Null ist
weil das Lager kein Drehmoment aufnehmen kann |
|
 |
SimonPhysik
Anmeldungsdatum: 08.11.2016
Beiträge: 72
|
 SimonPhysik Verfasst am: 10. Nov 2016 09:15 Titel: SimonPhysik Verfasst am: 10. Nov 2016 09:15 Titel: |
 |
|
|
Wie anders? |
|
 |
lh
Gast
|
 lh Verfasst am: 10. Nov 2016 09:40 Titel: lh Verfasst am: 10. Nov 2016 09:40 Titel: |
 |
|
Die Lösung ist richtig
das hat Myon auch so geschrieben
| Myon hat Folgendes geschrieben: | Damit das Drehmoment bezüglich r_0 verschwindet, muss gelten
|
Ich hatte das in der Formel nicht gleich erkannt  |
|
 |
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5852
|
 Myon Verfasst am: 10. Nov 2016 12:16 Titel: Myon Verfasst am: 10. Nov 2016 12:16 Titel: |
 |
|
Nur, damit es keine Missverständnisse gibt: Auf das Lager wirkt selbstverständlich ein Drehmoment, wenn die Massen abgebremst werden. Der Drehimpuls ändert sich ja. Das Drehmoment ist auch nicht abhängig von der Lage des Hindernisses.
Belastend für das Lager sind nicht Drehmomente, sondern Kräfte senkrecht zur Drehachse. Solche werden vermieden, wenn das Hindernis so positioniert wird, dass beim Abbremsvorgang das Drehmoment bezogen auf das Hindernis gleich null ist. |
|
 |
VeryApe

Anmeldungsdatum: 10.02.2008
Beiträge: 3247
|
 VeryApe Verfasst am: 10. Nov 2016 13:59 Titel: VeryApe Verfasst am: 10. Nov 2016 13:59 Titel: |
 |
|
| Zitat: | auf das Lager wirkt selbstverständlich ein Drehmoment, wenn die Massen abgebremst werden.
|
auf das Lager wirkt kein Drehmoment in Drehrechtung, egal welcher Fall, es sei denn du berücksichtigst Reibung.
und die Lösung ist völlig unabhängig von der Winkelbeschleunigung.
Oder Meinst das Drehmoment der Gewichtskräfte senkrecht zur Drehrichtung das durch das Lager kompensiert werden muß?
| Zitat: |
Belastend für das Lager sind nicht Drehmomente, sondern Kräfte senkrecht zur Drehachse. Solche werden vermieden, wenn das Hindernis so positioniert wird, dass beim Abbremsvorgang das Drehmoment bezogen auf das Hindernis gleich null ist.
|
was du damit meinst erschließt sich mir auch nicht.
Bei jedem anderen r0 wirkt einen tangentiale Kraft auf das Lager. r0 ist ausschließlich so zu setzen das diese tangentiale Kraft null. wird denn eine radiale hast du sowieso das reactio der Zentripetalkraft. ( weiß nicht wie man dies in der Physik nennt ich würde da auch im Inertialsystem Fliehkraft sagen)

DP Drehpunkt -- Drallsatz
=\sum m*a_{tangential}*r=F_{Hinderniss}*r_{0}+F_{Lager,tangential}*0=m_{1}*a_{1}*r_{1}+m_{2}*a_{2}*r_{2})

Forderung

_________________
WAS IST LOS IN EUROPA? https://www.youtube.com/watch?v=a9mduhSSC5w |
|
 |
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5852
|
 Myon Verfasst am: 10. Nov 2016 18:02 Titel: Myon Verfasst am: 10. Nov 2016 18:02 Titel: |
 |
|
@VeryApe
Zum ersten Punkt: Natürlich hast Du recht, auf das Lager wirkt kein Drehmoment. Was ich sagen wollte: Der Drehimpuls der beiden Massen bezüglich der Drehachse ändert sich, folglich muss ein Drehmoment bezüglich der Achse wirken. Dies ist ja auch offensichtlich, denn das Hindernis bremst den drehenden Balken und bewirkt dieses Drehmoment. Im weiteren: Ja, der Ort r_0 ist unabhängig von der Winkelbeschleunigung. Gewichtskräfte habe ich nicht berücksichtigt.
Zum zweiten Punkt: Du hast recht, durch die Kreisbewegung wirkt am Balken eine Kraft senkrecht zur Achse. Insofern müsste man genauer sagen: Es sollen möglichst keine zusätzlichen Kräfte auf die Achse wirken.
Wird das Hindernis "falsch" plaziert, wirkt eine resultierende Kraft auf den Balken, ja. Diese Betrachtung führt auf dasselbe Ergebnis wie die obige Forderung, dass bezüglich r_0 kein Drehmoment wirkt beim Abbremsen der beiden Massen. |
|
 |
|
















