| Autor |
Nachricht |
ph113
Anmeldungsdatum: 13.05.2016
Beiträge: 7
|
 ph113 Verfasst am: 14. Jun 2016 13:57 Titel: Frage zu "guten Zuständen" bei entarteter Störungs ph113 Verfasst am: 14. Jun 2016 13:57 Titel: Frage zu "guten Zuständen" bei entarteter Störungs |
 |
|
Meine Frage:
Hallo, ich habe eine Frage zu einer Erklärung in einem Buch, den Abschnitt seht ihr unten.
Ich verstehe die Erklärung ab dem Punkt nicht, wo man "in der anderen Richtung" vorangeht. Es wird behauptet, dass der obere Zustand auf eine Linearkombination von  und und  übergeht und der untere in eine "orthogonale" Linearkombination dieser beiden und man von vornherein nicht weiß, welche die "guten" Linearkombinationen sind. Später wird noch gesagt, dass übergeht und der untere in eine "orthogonale" Linearkombination dieser beiden und man von vornherein nicht weiß, welche die "guten" Linearkombinationen sind. Später wird noch gesagt, dass  und und  schon die "guten Linearkombinationen" waren und wir Glück hatten. schon die "guten Linearkombinationen" waren und wir Glück hatten.
Ich verstehe überhaupt nicht, woher man weiß, in welche Zustände der obere und untere Zustand aus dem Diagramm übergehen. Was ist eine orthogonale Linearkombination? Und welche Zustände sind die guten und warum?
Warum sind  und und  die guten Linearkombinationen, es sind doch nur Zustände und keine Linearkombinationen? die guten Linearkombinationen, es sind doch nur Zustände und keine Linearkombinationen?
Meine Ideen:
Später werden die guten Zustände mathematisch definiert als die Eigenfunktinoen eines Operators, der mit  und H' kommutiert und verschiedene Eigenwerte für diese beiden hat. Diese Erklärung ist mir völlig klar, nur verstehe ich die Erklärung oben überhaupt nicht. und H' kommutiert und verschiedene Eigenwerte für diese beiden hat. Diese Erklärung ist mir völlig klar, nur verstehe ich die Erklärung oben überhaupt nicht.
| Beschreibung: |
|
| Dateigröße: |
37.57 KB |
| Angeschaut: |
801 mal |

|
|
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18062
|
 TomS Verfasst am: 14. Jun 2016 21:33 Titel: TomS Verfasst am: 14. Jun 2016 21:33 Titel: |
 |
|
Ich verstehe nicht,was du nicht verstehst, aber ich probier's trotzdem:-)
Anstelle eines ungestörten Hamiltonoperators betrachten wir einfach eine 2 * 2 Matrix

Die Eigenzustände sind


sowie beliebige Linearkombinationen
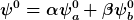
Die Eigenwerte sind trivialerweise

Für den vollen Hamiltonoperator einschließlich Störung betrachten wir die 2 * 2 Matrix

Die Eigenzustände sind identisch wie oben


mit den Eigenwerten

Allerdings sind nun die o.g. Linearkombinationen keine Eigenzustände mehr.
Nimm' doch spaßeshalber mal an, es wären die ungestörten Eigenzustände

zu den beiden Eigenwerten E gegeben.
Natürlich kannst du auch die o.g. gestörten Eigenfunktionen in diesen neuen ungestörten Eigenfunktionen entwickeln. Allerdings gilt nur in der o.g. ausgezeichneten Basis
 \stackrel{\epsilon \to 0}{\rightarrow} \psi^0_{a,b})
d.h. nur in dieser ausgezeichneten Basis sind die Eigenvektoren stetig im Parameter epsilon. Anders formuliert:
 \stackrel{\epsilon \to 0}{\not\rightarrow} \psi^0_\pm)
Man muss also die geeigneten Eigenvektoren finden, in denen das Problem auch im ungestörten, entarteten Zustand sinnvoll und stetig in der Störung beschrieben wird. Damit ergibt sich auch, welcher der beiden Eigenvektoren nun der "obere" und "welcher" der untere ist.
Allerdings kannst du das nie herausfinden, ohne die Störung selbst miteinzubeziehen.
|
|
 |
ph113
Anmeldungsdatum: 13.05.2016
Beiträge: 7
|
 ph113 Verfasst am: 14. Jun 2016 23:08 Titel: ph113 Verfasst am: 14. Jun 2016 23:08 Titel: |
 |
|
Hallo, erstmal vielen Dank für deine Mühe! Leider Blicke ich immer noch nicht ganz durch.
Dein Beispiel verstehe ich bis zu dem Punkt, wo du die ungestörten Eigenzustände +- einführst.
Was sind das für Zustände und was meinst du mit man kann die gestörten Eigenzustände auch in dieser Basis entwickeln, warum sollte man dies machen? Was ist diese ausgezeichnete Basis?
Abgesehen vom Beispiel weiß ich nicht, was eine orthogonale Linearkombination sein soll und woher man weiß, dass ein Zustand bei Abstellen der Störung in diesen orthogonalen übergeht und der andere nicht. Ich meine man könnte denken, dass beide oder keiner der Zustände in den orthogonalen übergehen, wie auch immer der definiert ist.
|
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18062
|
 TomS Verfasst am: 14. Jun 2016 23:57 Titel: TomS Verfasst am: 14. Jun 2016 23:57 Titel: |
 |
|
| ph113 hat Folgendes geschrieben: | Dein Beispiel verstehe ich bis zu dem Punkt, wo du die ungestörten Eigenzustände +- einführst.
Was sind das für Zustände und was meinst du mit man kann die gestörten Eigenzustände auch in dieser Basis entwickeln, warum sollte man dies machen? |
Stell' dir einfach mal vor, das Beispiel wäre wesentlich komplizierter, und du könntest die "guten" und zugleich einfachsten Zustände nicht einfach ablesen. Dann würdest du evtl. mit den +- Zuständen starten (letztlich kannst mit jeder beliebigen Linearkombination starten). Du würdest also in der +- Basis arbeiten, weil du dummerweise die "gute" Basis nicht gesehen hast.
Das ist nicht weiter schlimm, du darfst natürlich in jeder beliebigen Basis arbeiten. Nur du musst eben bedenken, dass die Basis, die du für die entarteten Zustände des ungestörten Hamiltonoperators verwendest, nicht unbedingt bereits die "gute" Basis ist, die du später für den gestören Hamiltonoperator benötigst. Du siehst dem ungestörten Hamiltonoperator und den Basen einfach nicht an, welche davon später für geeignete sein wird.
| ph113 hat Folgendes geschrieben: | | Was ist diese ausgezeichnete Basis? |
Die ursprüngliche a,b-Basis.
| ph113 hat Folgendes geschrieben: | | Abgesehen vom Beispiel weiß ich nicht, was eine orthogonale Linearkombination sein soll ... |
Du weißt, dass die ursprüngliche Basis orthonormiert ist:


Nun betrachtest Linearkombinationen


Nur wenn diese Linearkombinationen wiederum orthonormiert sind, liegt wieder eine Basis vor. D.h. man muss die Skalarprodukte berechnen und daraus die Bedingungen für die Koeffizienten ableiten:
^\dagger ( \alpha_2\psi_a + \beta_2\psi_b ) = \alpha_1^\ast\alpha_2 + \beta_1^\ast\beta_2 \stackrel{!}{=} 0)
sowie weitere Kombinationen.
Daraus folgt, dass die Koeffizienten eine unitäre Matrix bilden, die die Orthonormiertheit erhält.
| ph113 hat Folgendes geschrieben: | | ... und woher man weiß, dass ein Zustand bei Abstellen der Störung in diesen orthogonalen übergeht und der andere nicht. |
Die nicht mehr entarteten Eigenzustände des gestörten Hamiltonoperators definieren eine Basis. Die Störungstheorie setzt voraus, dass alle Ausdrücke stetig im Störungsparameter sind. Damit geht die gestörte Basis beim Abschalten der Störung stetig in genau eine (von unendlich vielen möglichen) ungestörten Basen über.
| ph113 hat Folgendes geschrieben: | | Ich meine man könnte denken, dass beide oder keiner der Zustände in den orthogonalen übergehen, wie auch immer der definiert ist. |
Was meinst du damit?
|
|
 |
ph113
Anmeldungsdatum: 13.05.2016
Beiträge: 7
|
 ph113 Verfasst am: 15. Jun 2016 21:31 Titel: ph113 Verfasst am: 15. Jun 2016 21:31 Titel: |
 |
|
Ok also ich habe mir das ganze nochmal angeschaut, ich denke, ich habe es etwas besser verstanden.
Um die Reihen in Lambda zu entwickeln, braucht man ja irgendeinen ungestörten Zustand, in den der gestörte Zustand für  übergeht. Den setzt man allgemein als Linearkombination der beiden Zustände an. Man möchte den Zustand so haben, dass am Ende die gleichen Energien wie bei der nichtentarteten Störungstheorie herauskommen, man also diese auch benutzten könnte. Daraus erhält man dann entweder übergeht. Den setzt man allgemein als Linearkombination der beiden Zustände an. Man möchte den Zustand so haben, dass am Ende die gleichen Energien wie bei der nichtentarteten Störungstheorie herauskommen, man also diese auch benutzten könnte. Daraus erhält man dann entweder 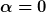 oder oder  . Stimmt das soweit? . Stimmt das soweit?
Das Enzige, was ich nicht verstehe, ist die Aussage, dass der obere Zustand in eine orthogonale und der untere in irgendeine Linearkombination übergeht. Ich weiß, was Orthogonalität von zwei verschiedenen Vektoren ist, aber eine Linearkombination ist doch nur ein Vektor, wie kann man hier von Orthogonalität sprechen? Und woran sieht man, dass die gestörten Zustände nur in der  , , Basis in die ungestörten übergehen? Basis in die ungestörten übergehen?
Hier fehlt mir leider noch das Verständnis.
|
|
 |
|
|
















