| Autor |
Nachricht |
kingcools
Anmeldungsdatum: 16.01.2011
Beiträge: 700
|
 kingcools Verfasst am: 05. Mai 2016 18:10 Titel: Diagonaler Operator kingcools Verfasst am: 05. Mai 2016 18:10 Titel: Diagonaler Operator |
 |
|
Hallo,
folgende Aufgabe habe ich:
 http://up.picr.de/25442988kj.jpg http://up.picr.de/25442988kj.jpg
Die ich hänge bei b) fest. So wie ich den Ausdruck verstehe, habe ich doch nur EINE (jede Transformation ersetzt ja die vorherige Variable durch eine neue) Variable und nicht etwa zwei, so dass ich nicht weiß, was ich unter Diagonal verstehen soll.
Also: Wie ist das Diagonal hier zu verstehen?
edit:
ich erhalte bei meiner bisherigen Herangehensweise bei b) als Ergebnis:
(FVF* Theta)(r) = (2/N)*exp((-2*pi*i/N)*r) * (Theta(0) + Theta(1) + ... + Theta(N-1))
Das sieht zwar schön aus, aber ergibt im Rahmen der Aufgabe nicht so viel Sinn. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18013
|
 TomS Verfasst am: 05. Mai 2016 18:27 Titel: TomS Verfasst am: 05. Mai 2016 18:27 Titel: |
 |
|
V ist eine Matrix, die den n-ten Einheitsvektor auf den (n+1)-ten Einheitsvektor abbildet. Diese Matrix solltest du mal explizit hinschreiben.
Der diagonale Operator V' ist dann eine Matrix, die ausschließlich auf der Hauptdiagonalen von Null verschiedene Einträge hat.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
kingcools
Anmeldungsdatum: 16.01.2011
Beiträge: 700
|
 kingcools Verfasst am: 05. Mai 2016 18:38 Titel: kingcools Verfasst am: 05. Mai 2016 18:38 Titel: |
 |
|
Verstehe ich nicht.
V wäre
V = {(0, 1, 0, ..., 0), (0,0,1,0,...,0), ... (0,...,1,0), (1,0,...,0)}.
Richtig?
Ich wüsste eigentlich eher gerne, ob ich überhaupt die Formel FVF* richtig verstehe. Die hat doch tatsächlich nur einen Parameter bzw. eine Variable, oder? Falls dem so ist, dann verstehe ich eben nicht, wieso man das Ergebnis als Matrix deuten kann. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18013
|
 TomS Verfasst am: 05. Mai 2016 19:09 Titel: TomS Verfasst am: 05. Mai 2016 19:09 Titel: |
 |
|
Ich lasse jetzt mal n = 0,1,2,... und den Spezialfall N-1 weg und betrachte einen unendlich-dimensionalen Hilbertraum.
Dann hast du den Verschiebeoperator
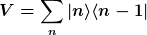
Für den Zustand psi gilt
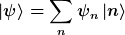
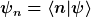
Der Verschiebeoperator wirkt gemäß
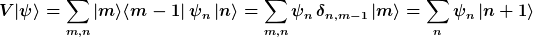
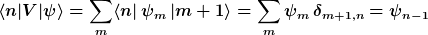
Soweit klar? (außer dass ich wohl V und V* irgendwie vertauscht bzw. +1 und -1 verwechselt habe)
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
kingcools
Anmeldungsdatum: 16.01.2011
Beiträge: 700
|
 kingcools Verfasst am: 05. Mai 2016 20:04 Titel: kingcools Verfasst am: 05. Mai 2016 20:04 Titel: |
 |
|
Hey, super für die Mühe, vielen Dank. Ich bin an die Dirac-Notation noch nicht so gewöhnt, daher kommentiere ich mal deine Zeilen, okay?
| TomS hat Folgendes geschrieben: |
Dann hast du den Verschiebeoperator
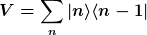
|
Das ist doch die Anwendung der Operatorendarstellung  in einer einer Basis, oder? in einer einer Basis, oder?
Die Basis hast du kurz notiert mit 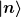 was nur kurz für "n-ter Basisvektor" steht. was nur kurz für "n-ter Basisvektor" steht.
| Zitat: |
Für den Zustand psi gilt
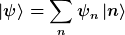
|
Einfach die Darstellung von 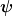 in der gewählten Basis wie üblich in der linearen Algebra. in der gewählten Basis wie üblich in der linearen Algebra.
| Zitat: |
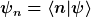
|
Das ist dann auch klar.
| Zitat: |
Der Verschiebeoperator wirkt gemäß
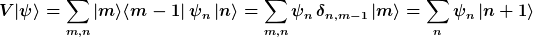
|
Das erste Gleichheitszeichen folgt aus Einsetzen der Operatordarstellung oben. Das zweite aus dem Skalarprodukt für Orthonormalbasen (sonst dürfte es kein Kroneckerdelta ergeben). Das dritte dann über die Summe über alle m. (Es muss ja n+1 = m <=> n = m-1 gelten).
| Zitat: |
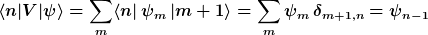
|
Das ist auch wieder nur Einsetzen der Operatordarstellung von der Gleichung zuvor und erneute Anwendung der "Orthonormalbasiseigenschaft" 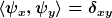
Soweit kann ich dir folgen. Und jetzt? |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18013
|
 TomS Verfasst am: 05. Mai 2016 20:20 Titel: TomS Verfasst am: 05. Mai 2016 20:20 Titel: |
 |
|
Jetzt stellst du F dar als
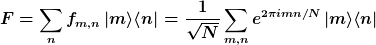
Dann überlegst du dir, was
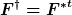
in dieser Matrixdarstellung bedeutet.
Dazu am besten mal mit einer 4*4 - Matrix explizit rumspielen ...
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
kingcools
Anmeldungsdatum: 16.01.2011
Beiträge: 700
|
 kingcools Verfasst am: 05. Mai 2016 22:00 Titel: kingcools Verfasst am: 05. Mai 2016 22:00 Titel: |
 |
|
|
Danke! Das hilft mir sehr weiter, denn mein ursprünglicher Fehler war, dass ich vergessen hatte, dass der adjungierte Operator ja bei Matrizen nicht nur konjugiert sondern auch transponiet wird haha. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18013
|
 TomS Verfasst am: 05. Mai 2016 23:15 Titel: TomS Verfasst am: 05. Mai 2016 23:15 Titel: |
 |
|
Nun setzt du
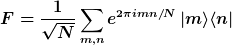
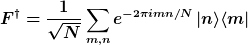
und berechnest
k/N})
Dabei fällt bei der Summenbildung nach Ausmultiplizieren ein Index wg. Orthonormiertheit und Kronecker-Delta weg.
Nun folgende Überlegung: du sollst die Unitarität von F beweisen, d.h. du musst zeigen, dass der letzte Ausdruck dem Eins-Operator entspricht. Dazu betrachtest du zwei Fälle:
Diagonalememente z = m - n = 0:
Der Exponent ist Null, die Summe daher gleich N, aufgrund des Vorfaktors 1/N erhältst du also Eins.
Nicht-Diagonalememente z = m - n > 0:
Zu berechnen ist die Summe
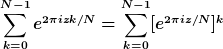
Dies entspricht der Partialsumme der geometrischen Reihe; damit zeigst du, dass dieser Ausdruck gleich Null ist.
Daraus folgt letztlich
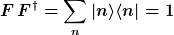 |
|
 |
kingcools
Anmeldungsdatum: 16.01.2011
Beiträge: 700
|
 kingcools Verfasst am: 06. Mai 2016 00:31 Titel: kingcools Verfasst am: 06. Mai 2016 00:31 Titel: |
 |
|
|
Hey danke, aber mein problem war eigentlich b), d.h. die Diagonalität von F V F* zu zeigen. Die Unitarität der Fouriertrafo hatte ich schon. Sorry, falls das unklar war :/ |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18013
|
 TomS Verfasst am: 06. Mai 2016 07:16 Titel: Re: Diagonaler Operator TomS Verfasst am: 06. Mai 2016 07:16 Titel: Re: Diagonaler Operator |
 |
|
Kein Thema.
| kingcools hat Folgendes geschrieben: | | So wie ich den Ausdruck verstehe, habe ich doch nur EINE Variable und nicht etwa zwei, so dass ich nicht weiß, was ich unter Diagonal verstehen soll. |
Verstehe ich nicht.
Evtl. verwirrt es dich, dass die Operatoren V, F, immer komponentenweise in ihrer Wirkung auf einen Vektor psi dargestellt sind; das ist tatsächlich unschön, und deswegen habe ich auch die Notation geändert; man erkennt die wesentlichen Eigenschaften - zumindest bei F - am Operator selbst, ohne dessen Wirkung auf spezielle Zustände.
Für b) würde ich zunächst mal exakt so vorgehen und
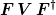
in der oben eingeführten Notation berechnen. Zunächst hast du sechs Summen über drei Indexpaare mk, pq, ln
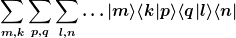
die zwei über p,q fallen bei Skalaproduktbildung
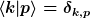
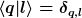
wg. Orthonormiertheit weg; es bleiben die Summen über m,k,l,n in der Form
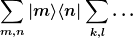
Evtl. kann man die innere Summe über k,l direkt ausführen und die Diagonalgestalt so wie für F direkt ablesen.
PS. Ist das eine Aufgabe in Mathe oder Physik? Ich halte die Notation für seltsam. Bedeutet F* hier den adjungierten Operator? Ich denke schon, aber das wird in der Physik dich durch einen "dagger" gekennzeichnet.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18013
|
 TomS Verfasst am: 06. Mai 2016 09:54 Titel: TomS Verfasst am: 06. Mai 2016 09:54 Titel: |
 |
|
Ich hab' jetzt ein bisschen weiter gerechnet. Mir erscheint das im wesentlichen identisch zum Beweis oben angeführten Beweis der Unitarität von F.
Zunächst mal ist V bereits diagonal, d.h. statt der Summe über das Indexpaar p,q tritt lediglich eine Summe über p auf. Dann erhält man eine Summe über p, die mittels der selben Methode der Partialsummen der geometrischen Reihe berechenbar ist.
Ich erhalte soetwas wie
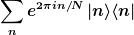
ACHTUNG: ich habe mir nicht die Mühe gemacht, den Sonderfall n = 0 bzw. n = N-1 in V zu betrachten; evtl. resultiert daraus noch eine Modifikation, aber im wesentlichen sollte das stimmen.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
|
















