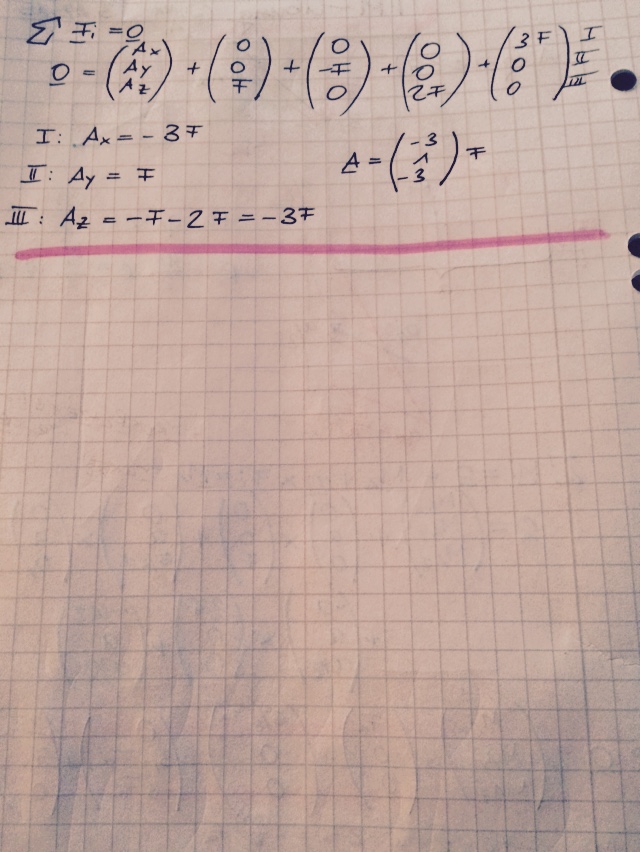| Autor |
Nachricht |
Claudini95
Anmeldungsdatum: 31.05.2015
Beiträge: 126
|
|
 |
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5863
Wohnort: jwd
|
 Mathefix Verfasst am: 07. Jan 2016 10:17 Titel: Mathefix Verfasst am: 07. Jan 2016 10:17 Titel: |
 |
|
Ein Moment um "A" ist deswegen vorhanden, weil ein Hebelarm der Länge " l"
von "A" bis "B" gegeben ist, an dem die eingezeichneten Kräfte angreifen.
|
|
 |
Claudini95
Anmeldungsdatum: 31.05.2015
Beiträge: 126
|
 Claudini95 Verfasst am: 07. Jan 2016 11:53 Titel: Claudini95 Verfasst am: 07. Jan 2016 11:53 Titel: |
 |
|
Hey Mathefix. Danke für die Antwort!
| Mathefix hat Folgendes geschrieben: | Ein Moment um "A" ist deswegen vorhanden, weil ein Hebelarm der Länge " l"
von "A" bis "B" gegeben ist, an dem die eingezeichneten Kräfte angreifen. |
Mit den eingezeichneten Kräften meinst du jetzt die Kraft  im Punkt B? Daraus ergibt sich das Moment. Sprich Aufgrund des Hebelarms und der Kraft. im Punkt B? Daraus ergibt sich das Moment. Sprich Aufgrund des Hebelarms und der Kraft.
Wie komme ich aber auf die Gleichung:

Ich erkenne einfach aus dem Schaubild nicht heraus wie sich die Größen ergeben. Ich sehe es einfach nicht 
Das wäre echt hilfreich, ich komme einfach nicht darauf 
Liebe Grüße
Claudia
|
|
 |
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5863
Wohnort: jwd
|
 Mathefix Verfasst am: 07. Jan 2016 14:16 Titel: Mathefix Verfasst am: 07. Jan 2016 14:16 Titel: |
 |
|
| Claudini95 hat Folgendes geschrieben: | Hey Mathefix. Danke für die Antwort!
| Mathefix hat Folgendes geschrieben: | Ein Moment um "A" ist deswegen vorhanden, weil ein Hebelarm der Länge " l"
von "A" bis "B" gegeben ist, an dem die eingezeichneten Kräfte angreifen. |

Ich erkenne einfach aus dem Schaubild nicht heraus wie sich die Größen ergeben. Ich sehe es einfach nicht 
Das wäre echt hilfreich, ich komme einfach nicht darauf 
Liebe Grüße
Claudia |
Kann die Hebelarme r_... in der Skizze nicht finden.
|
|
 |
Claudini95
Anmeldungsdatum: 31.05.2015
Beiträge: 126
|
 Claudini95 Verfasst am: 07. Jan 2016 14:34 Titel: Claudini95 Verfasst am: 07. Jan 2016 14:34 Titel: |
 |
|
Das ist es ja, in der Übung wurde die Ausführung (Einsetzen der Momente in die Formel) nicht hingeschrieben. Erst auf meine Anfrage kam dann das dunkel/schräggeschriebene dazu. Und dann wurde der Hebelarm (gepunktet angedeutet)
Und ich sitze an den Aufgaben schon geraume Zeit, weil immer entweder was ausgelassen wird und ich komme nie auf die Fährte des Verständnisses.. 
Claudia
|
|
 |
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5863
Wohnort: jwd
|
 Mathefix Verfasst am: 07. Jan 2016 15:09 Titel: Mathefix Verfasst am: 07. Jan 2016 15:09 Titel: |
 |
|
| Claudini95 hat Folgendes geschrieben: | Das ist es ja, in der Übung wurde die Ausführung (Einsetzen der Momente in die Formel) nicht hingeschrieben. Erst auf meine Anfrage kam dann das dunkel/schräggeschriebene dazu. Und dann wurde der Hebelarm (gepunktet angedeutet)
Und ich sitze an den Aufgaben schon geraume Zeit, weil immer entweder was ausgelassen wird und ich komme nie auf die Fährte des Verständnisses.. 
Claudia |
Ohne präzise Aufgabenstellung ist eine Lösung nicht möglich. 
Sorry
|
|
 |
Duncan
Gast
|
 Duncan Verfasst am: 07. Jan 2016 15:34 Titel: Duncan Verfasst am: 07. Jan 2016 15:34 Titel: |
 |
|
Die Aufgabe ist präzise und vollständig gestellt.
Die dunkle Schrift der Lösung enthält Fehler:
...der Hebelarm (gestrichelt) muss doch parallel zur y-Achse gezeichnet werden.
... man kann nicht Momente und Kräfte addieren.
|
|
 |
Claudini95
Anmeldungsdatum: 31.05.2015
Beiträge: 126
|
 Claudini95 Verfasst am: 07. Jan 2016 16:00 Titel: Claudini95 Verfasst am: 07. Jan 2016 16:00 Titel: |
 |
|
Hey Duncan.
Ja der gestrichelte Hebelarm ist nicht ganz parallel zur y-Achse. Sollte er aber sein. Ich verstehe das alles nicht.. Es gilt doch für das Drehmoment Kraft multipliziert mit dem Hebelarm. Der Vektor des Drehmoments ergibt sich wie ich schon gesagt habe aus dem Kreuzprodukt aus Abstandsvektor/Ortsvektor mit dem Kraftvektor.
Ich tue mich schon ehrlich gesagt beim Formulieren der Fragen schwer, weil ich nicht den roten Faden sehe.
Ich muss doch zuerst schauen wo meine Kräfte angreifen und den dazugehörigen Hebelarm wissen. Das bereitet mir schon Probleme. Ich habe doch 4 Kräfte die angreifen.
1. ganz oben auf B (also nur in z-Richtung)
2. seitlich auf E
3. auf der Strecke E-C
4. quer auf der Strecke C-D
Oder nicht? Und die Hebelarme sind quasi die Strecken?
Dabei muss ich aber immer die Richtungen berücksichtigen.
Also bei
1. muss der Hebelarm a in y-Richtung sein
2. ist der Hebelarm -a/2 in x-Richtung a in y-Richtung und in z-Richtung a/2
(Das kann ich gerade nicht nachvollziehen)
3. Sehe ich nicht. 
4. auch nicht.
Also das Koordinatensystem ist oben rechts festgelegt. Ich erkenne leider nicht in allen Fällen in welche Richtungen die Hebelarme verlaufen. Meno =(
Danke Euch!
Claudia
|
|
 |
Duncan
Gast
|
 Duncan Verfasst am: 07. Jan 2016 17:57 Titel: Duncan Verfasst am: 07. Jan 2016 17:57 Titel: |
 |
|
Stelle zunächst mal das Kräftegleichgewicht auf.
Kräfte:
in x-Richtung: Ax + 3F = 0
in y-Richtung: Ay - F = 0
in z-Richtung: Az + 3F = 0
Erst dann die Momente.
(Hebelarm = Entfernung der Kraftwirkungslinie vom Punkt A und zwar in x-, y-, und z-Richtung.
|
|
 |
Claudini95
Anmeldungsdatum: 31.05.2015
Beiträge: 126
|
 Claudini95 Verfasst am: 07. Jan 2016 19:58 Titel: Claudini95 Verfasst am: 07. Jan 2016 19:58 Titel: |
 |
|
| Duncan hat Folgendes geschrieben: | Stelle zunächst mal das Kräftegleichgewicht auf.
|
Ahso. Also quasi alle Kräfte in in die einzelnen Richtungen aufgesplittet.
Die Ax und Ay und Az sind aber wo genau? Die kann ich nicht wiederfinden.
Danke
Claudia
|
|
 |
Duncan
Gast
|
 Duncan Verfasst am: 07. Jan 2016 20:07 Titel: Duncan Verfasst am: 07. Jan 2016 20:07 Titel: |
 |
|
Die Auflagerkraft A wirkt im Punkt A.
Sie wird in die Komponenten Ax, Ay, Az zerlegt.
|
|
 |
Claudini95
Anmeldungsdatum: 31.05.2015
Beiträge: 126
|
 Claudini95 Verfasst am: 07. Jan 2016 20:35 Titel: Claudini95 Verfasst am: 07. Jan 2016 20:35 Titel: |
 |
|
Ahso okay. Nun bereitet mir noch die y-Richtung und z-Richtung der Kräfte Probleme. In x-Richtung sehe ich die 3F an E. Aber wieso ist in y-Richtung die Kraft -F? Gemeint ist wohl die Kraft zwischen C-D. Mit dem Minuszeichen okay es zeigt in die entgegengesetzte Richtung von y, das sehe ich noch, aber den Faktor 3? Wieso? In z-Richtung +3F? Ich sehe da nur das F an Punkt B.
Sorry 
Danke!
Claudia
|
|
 |
Duncan
Gast
|
 Duncan Verfasst am: 07. Jan 2016 20:57 Titel: Duncan Verfasst am: 07. Jan 2016 20:57 Titel: |
 |
|
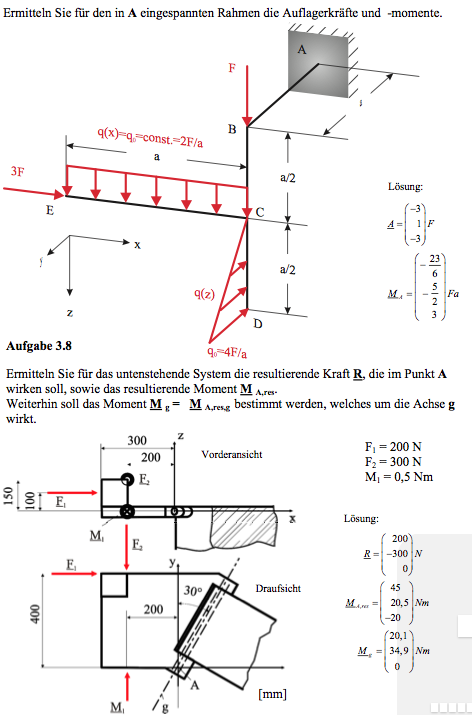
In negativer y-Richtung wirkt die Streckenlast auf den Stab CD.
Sie ist im Punkt C = 0 und wächst linear bis zum Endwert = 4F/a im Punkt D an.
Ihre Resultierende ist daher F und ihr Angriffspunkt bei z = 5/6*a.
In z-Richtung wirkt die Kraft F im Punkt B und die Gleichlast auf den Stab EC.
Die Gleichlast ist mit 2F/a und die Stablänge mit a gegeben. Dies ergibt eine Resultierende von 2F auf die Stabmitte.
Insgesamt also 3F in z-Richtung.
Hast du denn noch nie einen Grundkurs über Mechanik gehabt?
|
|
 |
Claudini95
Anmeldungsdatum: 31.05.2015
Beiträge: 126
|
 Claudini95 Verfasst am: 07. Jan 2016 21:22 Titel: Claudini95 Verfasst am: 07. Jan 2016 21:22 Titel: |
 |
|
Endlich sehe ich was nützliches aus dem Gebilde! Danke für die Nachricht, die hat mir jetzt einiges erklärt, wirklich Dankeschön.
Okay jetzt habe ich das Prinzip verstanden
in x-Richtung: Ax + 3F = 0
in z-Richtung: Az + F + 2F = 0 (quasi die Gleichlast und die Kraft im Punkt B)
in negative y-Richtung kann ich es noch nicht komplett verstehen. Wir haben eine Funktion abhängig von dem Ort z. Sie wächst linear. Im Punkt D hat sie eine Kraft von 4F pro Längeneinheit a. Ich hätte jetzt gesagt da wir eine Stablänge von a/2 haben wäre dann die Kraft 2F. Die Resultierende F, verstehe ich nicht ebenso wie ihren Angriffspunkt z = 5/6*a.
| Duncan hat Folgendes geschrieben: |
Hast du denn noch nie einen Grundkurs über Mechanik gehabt? |
Also ich gehe zu der Vorlesung, aber da wird nur hergeleitet und gar keine Praxis gemacht. Daher gehen auch zu der Vorlesung von Anfangs 200 Leuten nur noch 10% hin.. In der Übung naja.. da sitzen wir zu fünft... von anfangs 29..
Claudia
|
|
 |
Duncan
Gast
|
 Duncan Verfasst am: 08. Jan 2016 09:03 Titel: Duncan Verfasst am: 08. Jan 2016 09:03 Titel: |
 |
|
In y-Richtung wirkt (nur) die gezeichnete Dreieckslast und zwar in negativer Richtung.
Die Gesamtkraft entspricht dem Flächeninhalt des Dreiecks, also:
Fgesamt = 1/2*a/2*4F/a = F
Die Wirkungslinie dieser Kraft zeigt in negative y-Richtung und geht durch den Schwerpunkt des Dreiecks.
Schwerpunkt liegt 2/3*a/2 unter der oberen Ecke C, also bei z-Koordinate = 5/6*a.
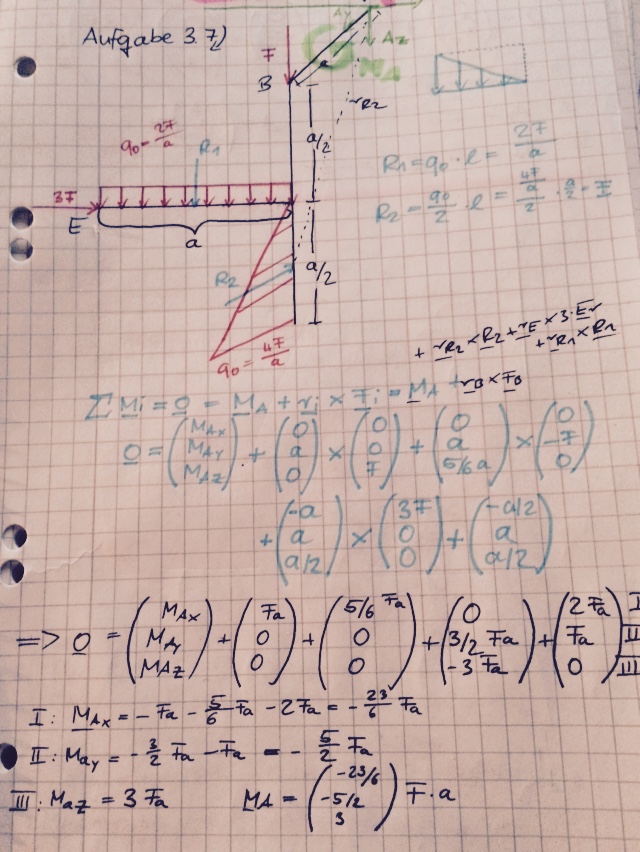
Jetzt zu den Momenten:
Wähle für jede Kraft einen Punkt P auf ihrer Wirkungslinie.
Dann ist ri der Vektor AP.
Das Drehmoment dieser Kraft bezüglich A:
Mi = ri X Fi. (Vektorprodukt)
|
|
 |
Claudini95
Anmeldungsdatum: 31.05.2015
Beiträge: 126
|
 Claudini95 Verfasst am: 08. Jan 2016 14:00 Titel: Claudini95 Verfasst am: 08. Jan 2016 14:00 Titel: |
 |
|
| Duncan hat Folgendes geschrieben: | In y-Richtung wirkt (nur) die gezeichnete Dreieckslast und zwar in negativer Richtung.
Die Gesamtkraft entspricht dem Flächeninhalt des Dreiecks, also:
Fgesamt = 1/2*a/2*4F/a = F |
Genau das ist Grundseite multipliziert mit der Höhe geteilt durch 2. Das erkenne ich. Aber weshalb entspricht die Gesamtkraft dem Flächeninhalt des Dreiecks? Da habe ich Probleme es nachzuvollziehen. Wie kann ich mir das vorstellen?
| Duncan hat Folgendes geschrieben: | | Schwerpunkt liegt 2/3*a/2 unter der oberen Ecke C, also bei z-Koordinate = 5/6*a. |
Der Schwerpunkt des Dreiecks ist
 ) quasi ein Mittelwert, der einzelnen Strecken quasi ein Mittelwert, der einzelnen Strecken
,\quad y_s = \frac13(y_A+y_B+y_C) ) mit den Koordinaten der Eckpunkte. mit den Koordinaten der Eckpunkte.
Brauchen wir nur die z-Koordinate des Schwerpunktes? Weil die Kraft ja in negative y-Richtung wirkt und zwar senkrecht auf die z-Richtung? Und es liegt ja in der y-z-Ebene oder sehe ich das falsch?
Wie komme ich aber auf die Wirkungslinien? Es ist ja so, dass eine Kraft an einem starren Körper entlang seiner Wirkungslinie verschoben werden darf, ohne dass sich die Wirkung der Kraft auf diesen Körper ändert. Aber wie wähle ich diese Punkte dann?
Dankeschön,
Claudia
|
|
 |
Duncan
Gast
|
 Duncan Verfasst am: 09. Jan 2016 17:56 Titel: Duncan Verfasst am: 09. Jan 2016 17:56 Titel: |
 |
|
Den Schwerpunkt des Dreiecks rechnet man nicht mit deiner Formel sondern mit elementarster Dreiecksgeometrie.
Sei also die resultierende Kraft der Dreiecksbelastung R1.
Vektoriell geschrieben:

Als Punkt wählen wir einen Punk auf der Wirkungslinie von R1:

Dies ergibt M1 = r1 X F1

Genauso für die übrigen Kräfte.
Gesamtmoment M ist dann die Summe aller Mi.
Achtung: das Auflagermoment ist dann der negative Wert von M.
|
|
 |
Claudini95
Anmeldungsdatum: 31.05.2015
Beiträge: 126
|
 Claudini95 Verfasst am: 09. Jan 2016 20:14 Titel: Claudini95 Verfasst am: 09. Jan 2016 20:14 Titel: |
 |
|
| Duncan hat Folgendes geschrieben: | | Den Schwerpunkt des Dreiecks rechnet man nicht mit deiner Formel sondern mit elementarster Dreiecksgeometrie. |
Also ich habe mir etliche Formeln angesehen dafür, über meine erwähnte Berechnung, über Seitenhalbierende, nachvollziehen kann ich die von dir bezeichnete "einfachste" Geometrie immer noch nicht. Das bereitet mir noch Probleme. Mit der Wirkungslinie stehe ich auch noch ein wenig auf Kriegsfuß 
| Duncan hat Folgendes geschrieben: |
Sei also die resultierende Kraft der Dreiecksbelastung R1.
Vektoriell geschrieben:

Als Punkt wählen wir einen Punk auf der Wirkungslinie von R1:

Dies ergibt M1 = r1 X F1

Genauso für die übrigen Kräfte.
Gesamtmoment M ist dann die Summe aller Mi.
Achtung: das Auflagermoment ist dann der negative Wert von M. |
Ich glaube du meinst das so: 
Ist ja negativ. Im Punkt B haben wir ja die Kraft F in z- Richtung und der Abstand ist a sprich, wie in der "Musterlösung":

Im Punkt E müsste es doch eig auch stimmen wie in der "Musterlösung", wenn man den Abstandsvektor von dem Koordinatenursprung nimmt?

Bei der Gleichlast ist in der "Musterlösung" für mich unklar wieder was gemacht wurde. Da bestimmt man nur den Vektor zum Mittelpunkt der Strecke E-C?
Danke dir Duncan. Sry für die blöden Fragen, aber ich weiß es echt nicht:(
Ich bemühe mich zu bessern!
Claudia
|
|
 |
Duncan
Gast
|
 Duncan Verfasst am: 09. Jan 2016 21:31 Titel: Duncan Verfasst am: 09. Jan 2016 21:31 Titel: |
 |
|
Woher nimmst du die Minuszeichen?
Geometrie des Dreiecks:
Eine Parallele zu einer Dreiecksseite, die durch den Schwerpunkt des Dreiecks geht, teilt die beiden anderen Dreiecksseiten im Verhältnis 2:1.
|
|
 |
Claudini95
Anmeldungsdatum: 31.05.2015
Beiträge: 126
|
 Claudini95 Verfasst am: 09. Jan 2016 21:58 Titel: Claudini95 Verfasst am: 09. Jan 2016 21:58 Titel: |
 |
|
| Duncan hat Folgendes geschrieben: | | Woher nimmst du die Minuszeichen? |
Nirgends. Die sind doch da.
Bei  ist das Minus gegeben durch die negative y-Richtung. ist das Minus gegeben durch die negative y-Richtung.
Bei 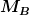 ist das Minus falsch, vor dem Vektor. Hast recht. ist das Minus falsch, vor dem Vektor. Hast recht.
Bei  ist auch das Minus falsch vor dem Vektor habe es beim Kopieren wohl ausversehen mitgeschleppt. ist auch das Minus falsch vor dem Vektor habe es beim Kopieren wohl ausversehen mitgeschleppt.
| Duncan hat Folgendes geschrieben: | | Eine Parallele zu einer Dreiecksseite, die durch den Schwerpunkt des Dreiecks geht, teilt die beiden anderen Dreiecksseiten im Verhältnis 2:1. |
Hm. Dreieck, eine parallele zu einer der drei Dreiecksseiten durch den Schwerpunkt teilt die anderen zwei Dreieckseigen im Verhältnis 2:1. Wenn ich mir das aufzeichne, dann werden die Seiten eher zu 1:3 und 2:3 geteilt im Schnittpunkt.. 
Danke
Claudia
|
|
 |
Duncan
Gast
|
 Duncan Verfasst am: 10. Jan 2016 09:06 Titel: Duncan Verfasst am: 10. Jan 2016 09:06 Titel: |
 |
|
Bei M1 ist nicht der Kraftvektor falsch sondern das Resultat.
Teilungsverhältnis einer Strecke:
Wie viel ist denn 2/3 zu 1/3 ?
Streckenlasten: siehe .youtube.com/watch?v=QBU_p36AhZ8
(vorher www tippen).
|
|
 |
Claudini95
Anmeldungsdatum: 31.05.2015
Beiträge: 126
|
 Claudini95 Verfasst am: 10. Jan 2016 09:42 Titel: Claudini95 Verfasst am: 10. Jan 2016 09:42 Titel: |
 |
|
| Duncan hat Folgendes geschrieben: | | Bei M1 ist nicht der Kraftvektor falsch sondern das Resultat. |
Was ist denn da falsch, man darf das Minuszeichen doch vorziehen?
| Duncan hat Folgendes geschrieben: |
Teilungsverhältnis einer Strecke:
Wie viel ist denn 2/3 zu 1/3 ?
|
Ja der Unterschied liegt bei 1/3. Okay das eine ist dann das doppelte des anderen also 2:1.
| Duncan hat Folgendes geschrieben: |
Streckenlasten: siehe .youtube.com/watch?v=QBU_p36AhZ8
(vorher www tippen). |
Danke! Von den Videos werde ich Gebrauch machen. (Also den anderen auch)
Aber laut Video hätten wir dann bei unserem Dreieck doch die Höhe  multipliziert mir der Grundseite also multipliziert mir der Grundseite also 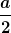 geteilt durch 2. geteilt durch 2.

Danke!
Claudia
|
|
 |
Duncan
Gast
|
 Duncan Verfasst am: 10. Jan 2016 10:43 Titel: Duncan Verfasst am: 10. Jan 2016 10:43 Titel: |
 |
|
| Claudini95 hat Folgendes geschrieben: | man darf das Minuszeichen doch vorziehen?
Ja, aber dann richtig rechnen!
Aber laut Video hätten wir dann bei unserem Dreieck doch die Höhe  multipliziert mir der Grundseite also multipliziert mir der Grundseite also 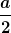 geteilt durch 2. geteilt durch 2. |
Richtig!
|
|
 |
Claudini95
Anmeldungsdatum: 31.05.2015
Beiträge: 126
|
 Claudini95 Verfasst am: 10. Jan 2016 11:44 Titel: Claudini95 Verfasst am: 10. Jan 2016 11:44 Titel: |
 |
|
Aber wieso ist dann unsere z-Komponente dann  und was das mit dem Verhältnis 2:1 zu tun. Mir ist jetzt klargeworden, dass die Resultierende eines Dreiecks durch den Schwerpunkt geht. (wie im Video und von dir gesagt). und was das mit dem Verhältnis 2:1 zu tun. Mir ist jetzt klargeworden, dass die Resultierende eines Dreiecks durch den Schwerpunkt geht. (wie im Video und von dir gesagt).
die Höhe 
Grundseite also 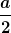
Berechnung Flächeninhalt des Dreiecks:

Resultierende ist somit jetzt klar geworden, danke!
| Duncan hat Folgendes geschrieben: |
Ihre Resultierende ist daher F und ihr Angriffspunkt bei z = 5/6*a. ...
...Schwerpunkt liegt 2/3*a/2 unter der oberen Ecke C, also bei z-Koordinate = 5/6*a.
|

Ich komme einfach nicht auf die 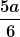 
| Duncan hat Folgendes geschrieben: |
Ja, aber dann richtig rechnen! |
Wo habe ich denn falsch gerechnet?
Claudia
|
|
 |
Duncan
Gast
|
 Duncan Verfasst am: 10. Jan 2016 17:40 Titel: Duncan Verfasst am: 10. Jan 2016 17:40 Titel: |
 |
|
Der Koordinatenursprung liegt im Punkt A.
Wo du das Kreuzprodukt falsch gerechnet hast, kann ich nicht sagen.
|
|
 |
Claudini95
Anmeldungsdatum: 31.05.2015
Beiträge: 126
|
 Claudini95 Verfasst am: 10. Jan 2016 17:51 Titel: Claudini95 Verfasst am: 10. Jan 2016 17:51 Titel: |
 |
|
| Duncan hat Folgendes geschrieben: | Der Koordinatenursprung liegt im Punkt A.
|
Hey, ja aber ich weiß gerade nicht was du mir damit sagen willst..
| Duncan hat Folgendes geschrieben: |
Wo du das Kreuzprodukt falsch gerechnet hast, kann ich nicht sagen. |

Dann wohl ohne Minus. Wenn man den Flächeninhalt berechnet dann kommt ja F heraus. Aber die Kraft zeigt doch eig in negative y-Richtung, daher weiß ich nicht wieso ist das Minus da herausnehmen soll 
Die  in der z-Komponente, ich verstehe es nicht in der z-Komponente, ich verstehe es nicht 
bitte 
Claudia
EDIT:
Schon okay es kommt ja  also + heraus. also + heraus.
|
|
 |
Duncan
Gast
|
 Duncan Verfasst am: 10. Jan 2016 18:14 Titel: Duncan Verfasst am: 10. Jan 2016 18:14 Titel: |
 |
|
Der Kraftvektor enthält ein Minuszeichen, das Kreuzprodukt aber nicht.
Die resultierende Kraft der Dreieckslast liegt 2/3*a/2 unterhalb des Punktes C. Dieser hat die z-Koordinate a/2.
Also hat die Resultierende die z-Koordinate a/2+2/3*a/2 = 5/6*a.
|
|
 |
Claudini95
Anmeldungsdatum: 31.05.2015
Beiträge: 126
|
 Claudini95 Verfasst am: 10. Jan 2016 19:20 Titel: Claudini95 Verfasst am: 10. Jan 2016 19:20 Titel: |
 |
|
| Duncan hat Folgendes geschrieben: | | Der Kraftvektor enthält ein Minuszeichen, das Kreuzprodukt aber nicht. |
Ja genau.
| Duncan hat Folgendes geschrieben: | Der Kraftvektor enthält ein Minuszeichen, das Kreuzprodukt aber nicht.
Die resultierende Kraft der Dreieckslast liegt 2/3*a/2 unterhalb des Punktes C. Dieser hat die z-Koordinate a/2.
Also hat die Resultierende die z-Koordinate a/2+2/3*a/2 = 5/6*a. |
Also so wie ich es verstehe. Die Seitenlänge des Dreiecks (die Seite auf der z-Achse liegend ist a/2). Die Höhe des Schwerpunktes bzw. die Koordinate ist dann quasi 2/3 * a/2 aber wieso addieren wie da noch a/2 drauf?
Ich bin doch quasi wenn ich die Resultierende Kraft auf 2/3 * a/2 habe im Schwerpunkt? Wieso addiere ich dann noch die a/2 drauf?
Danke,
Claudia
|
|
 |
Duncan
Gast
|
 Duncan Verfasst am: 10. Jan 2016 19:33 Titel: Duncan Verfasst am: 10. Jan 2016 19:33 Titel: |
 |
|
Weil ja das Moment bezüglich des Punktes A gesucht ist.
Also muss r von A aus gemessen werden.
|
|
 |
Claudini95
Anmeldungsdatum: 31.05.2015
Beiträge: 126
|
 Claudini95 Verfasst am: 10. Jan 2016 19:44 Titel: Claudini95 Verfasst am: 10. Jan 2016 19:44 Titel: |
 |
|
Ahso. Ja und der Abstand zu A (jedenfalls in z-Richtung) von C zu B, sprich um auf die Höhe von A zu kommen ist a/2, richtig? Aber irgendwie ergibt das für mich keinen Sinn. Das ist dann aber trotzdem doch nicht auf Höhe vom Punkt a. Verstehst du was ich meine?
Ich danke!
Claudia
|
|
 |
Duncan
Gast
|
 Duncan Verfasst am: 11. Jan 2016 12:42 Titel: Duncan Verfasst am: 11. Jan 2016 12:42 Titel: |
 |
|
Nein, ich verstehe nicht was du meinst.
Wenn du Ds Beispiel aber noch immer nicht verstehst, so rate ich dir, dich zunächst mit einfacheren Aufgaben zu beschäftigen.
|
|
 |
Claudini95
Anmeldungsdatum: 31.05.2015
Beiträge: 126
|
 Claudini95 Verfasst am: 11. Jan 2016 16:33 Titel: Claudini95 Verfasst am: 11. Jan 2016 16:33 Titel: |
 |
|
| Duncan hat Folgendes geschrieben: |
Wenn du Ds Beispiel aber noch immer nicht verstehst, so rate ich dir, dich zunächst mit einfacheren Aufgaben zu beschäftigen. |
Das habe ich. Im Prinzip ist aber nur der eine Punkt unklar... Ich glaube aber, dass ich ihn verstanden habe. Also wie erwähnt ist die resultierende Kraft:

Diese Kraft geht durch den Schwerpunkt des Dreiecks und zwar in negative y-Richtung. Wir wollen alle Auflagekräfte und Auflagemomente im Punkt A bestimmen. Wir befinden uns jedoch mit der resultierenden Kraft auf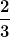 der Länge der Strecke von der Länge der Strecke von 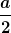 ? ?
Was du ja auch meintest:
| Duncan hat Folgendes geschrieben: | | Die resultierende Kraft der Dreieckslast liegt 2/3*a/2 unterhalb des Punktes C |
(Ich konnte es einfach nicht nachvollziehen)
Wie in dem Video erklärt wurde greift ja die Resultierende  von dem rechten Winkel an. Sprich um zum Punkt zu gelangen, muss ich von dem rechten Winkel an. Sprich um zum Punkt zu gelangen, muss ich  rechnen (um zum Punkt C zu gelangen) und darauf noch rechnen (um zum Punkt C zu gelangen) und darauf noch 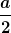 addieren um zum Punkt A (in z-Richtung zu gelangen). addieren um zum Punkt A (in z-Richtung zu gelangen).
Endlich! 
Danke!
Claudia
|
|
 |
Duncan
Gast
|
 Duncan Verfasst am: 11. Jan 2016 20:27 Titel: Duncan Verfasst am: 11. Jan 2016 20:27 Titel: |
 |
|
Ich zeige dir noch das 2. Beispiel Aufgabe 3.8:
(Einheiten nicht geschrieben, Vektorgrößen nicht gekennzeichnet)
Kräfte:

Moment bezüglich A:

Achse g:
\\cos(30°\\0\end{pmatrix}=\begin{pmatrix}0,5\\0,866\\0\end{pmatrix})
Projektion von MAres auf die Achse g:

|
|
 |
Claudini95
Anmeldungsdatum: 31.05.2015
Beiträge: 126
|
|
 |
Duncan
Gast
|
 Duncan Verfasst am: 12. Jan 2016 10:18 Titel: Duncan Verfasst am: 12. Jan 2016 10:18 Titel: |
 |
|
Die Musterlösung ist richtig.
Siehe auch meine Rechnung.
Weshalb soll denn ∑ M =0 sein?
|
|
 |
Claudini95
Anmeldungsdatum: 31.05.2015
Beiträge: 126
|
 Claudini95 Verfasst am: 12. Jan 2016 10:59 Titel: Claudini95 Verfasst am: 12. Jan 2016 10:59 Titel: |
 |
|
| Duncan hat Folgendes geschrieben: | Die Musterlösung ist richtig.
|
Ja?
| Duncan hat Folgendes geschrieben: |
Weshalb soll denn ∑ M =0 sein? |
Das steht aber in der Musterlösung..
Summe aller Einzeldrehmomente um einen Drehpunkt ergibt doch Null?
Wo ist denn mein Denkfehler bzw. wo mache ich falsche Annahmen. Der Punkt A ist fest genauso wie die Wahl der Koordinaten. Welche Aussagen von mir sind nicht richtig?
Danke
Claudia
|
|
 |
Duncan
Gast
|
 Duncan Verfasst am: 12. Jan 2016 13:11 Titel: Duncan Verfasst am: 12. Jan 2016 13:11 Titel: |
 |
|
Ich möchte diesen Thread nicht endlos fortsetzen und empfehle dir nochmals, dich zunächst mit einfacheren Aufgaben zu beschäftigen.
Aber vielleicht hilft hier ein anderer aus dem Forum weiter.
|
|
 |
Claudini95
Anmeldungsdatum: 31.05.2015
Beiträge: 126
|
 Claudini95 Verfasst am: 13. Jan 2016 08:59 Titel: Claudini95 Verfasst am: 13. Jan 2016 08:59 Titel: |
 |
|
Ja ich weiß, das dauert lange, aber die erste Aufgabe habe ich verstanden jetzt, bei der zweiten ist es eig eine Frage wie man doch das Koordinatensystem legt? Somit ergeben sich andere Ortsvektoren. Ich weiß aber manchmal nicht worauf du hinaus willst wie mit der Frage weshalb die Summe der Momente Null sein soll? Du fragst mich was ich antworte und dann gehst du auf manches nicht mehr ein und ich weiß nicht ob es falsch ist. Ich bin dir echt dankbar für deine Zeit die du hier investiert hast und deine Hilfe, wirklich das ist echt super nett. Ich will es aber wirklich verstehen und Übung macht nunmal den Meister.
Ich weiß nicht wieso, aber ich habe anfangs die Ortsvektoren anstatt vom Ursprung zum Kraftvektor, andersrum also vom Kraftvektor zum Ursprung bestimmt. Deshalb komme ich auf die gleiche Variante nur mit Vorzeichenwechsel. Ich bin am Hadern mit dem Ortsvektor  . Normalerweise hat dieser doch die Länge 1? Den Zweck erfasse ich bei der Lösung auch noch nicht. . Normalerweise hat dieser doch die Länge 1? Den Zweck erfasse ich bei der Lösung auch noch nicht.
Vielen Dank!
Claudia
PS: Noch bisschen Geduld bitte mit Claudummi 
|
|
 |
Duncan
Gast
|
 Duncan Verfasst am: 13. Jan 2016 11:39 Titel: Duncan Verfasst am: 13. Jan 2016 11:39 Titel: |
 |
|
Zuerst möchte ich noch ein kleines Missverständnis ausräumen:
für mich ist die „Musterlösung“ die „Lösung“, die bei der Aufgabenstellung
(erster Beitrag) angegeben ist. Diese Lösung ist richtig und stimmt mit meiner Rechnung überein.
Du scheinst die handschriftliche Rechnung als „Musterlösung“ anzusehen. Obwohl dies nirgends vermerkt ist.
Diese handschriftliche Rechnung enthält Fehler. Dort wird auch ∑ F=0 und ∑ M=0 gesetzt. Dies ist Unsinn und führt zum falschen Resultat. (negative Werte).
Als Hebelarm für Drehmomente ist ganz einfach der Abstand der Kraftwirkungslinie zum Bezugspunkt einzusetzen.
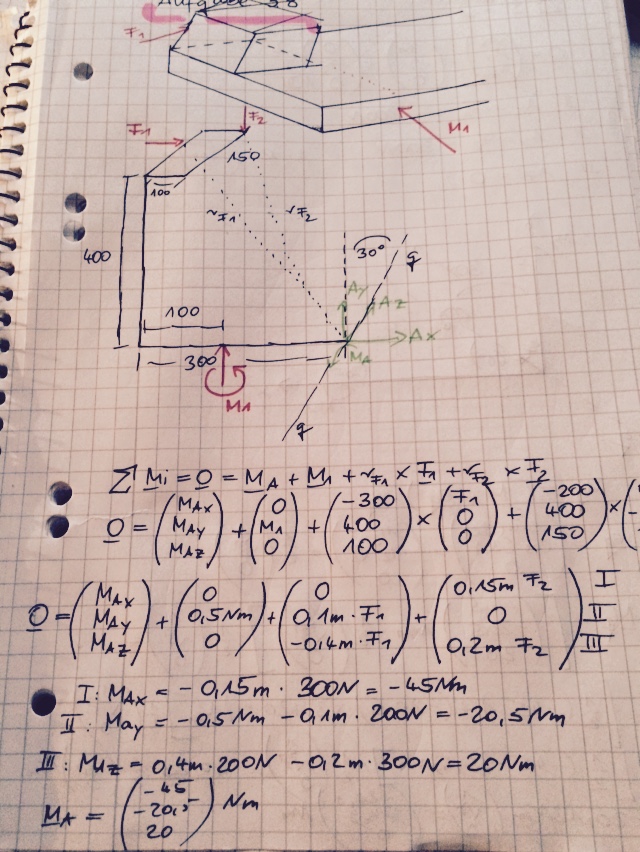
Z.B. für die Kraft F1 ergibt sich das Moment bezüglich A:
F1*0 in x-Richtung
F1*0,1 m in y-Richtung
F1*0,4 m in z-Richtung.
|
|
 |
Claudini95
Anmeldungsdatum: 31.05.2015
Beiträge: 126
|
 Claudini95 Verfasst am: 14. Jan 2016 08:33 Titel: Claudini95 Verfasst am: 14. Jan 2016 08:33 Titel: |
 |
|
| Duncan hat Folgendes geschrieben: | Zuerst möchte ich noch ein kleines Missverständnis ausräumen:
für mich ist die „Musterlösung“ die „Lösung“, die bei der Aufgabenstellung
(erster Beitrag) angegeben ist. Diese Lösung ist richtig und stimmt mit meiner Rechnung überein.
Du scheinst die handschriftliche Rechnung als „Musterlösung“ anzusehen. Obwohl dies nirgends vermerkt ist.
|
Ja genau so habe ich es angenommen.
| Duncan hat Folgendes geschrieben: |
Diese handschriftliche Rechnung enthält Fehler. Dort wird auch ∑ F=0 und ∑ M=0 gesetzt. Dies ist Unsinn und führt zum falschen Resultat. (negative Werte).
|
Wieso ist denn die Summe der Kräfte gleich Null und die Summe der Momente gleich Null Unsinn? Es sind doch die Grundregeln?
| Duncan hat Folgendes geschrieben: |
Als Hebelarm für Drehmomente ist ganz einfach der Abstand der Kraftwirkungslinie zum Bezugspunkt einzusetzen.
Z.B. für die Kraft F1 ergibt sich das Moment bezüglich A:
F1*0 in x-Richtung
F1*0,1 m in y-Richtung
F1*0,4 m in z-Richtung. |
Das kann aber nicht stimmen. Die Kraft liegt hat auch eine x-Koordinate Null ist. Wir haben doch eine x-Komponente von -300mm. Die kann doch nicht Null sein. In der Vorderansicht sieht man doch, dass vom Punkt A (Ursprung) ein Versatz in negative x-Richtung von -300mm da ist?
Also nach meinem Stand ist jetzt:
 richtig. richtig.
Kann es sein, dass du die y- und z-Richtung vertauscht hast? Es kann nicht stimmen.

Sollte auch stimmen. Wir haben in beiden Fällen x,y und z Komponenten vom Bezugspunkt A zu den Kräften F.
Die Kräfte wirken jeweils nur in eine Richtung. Sprich F1 in x-Richtung mit Wert 200N und F2 in negative y-Richtung mit Wert -300N. Da sind die anderen Komponenten ja Null.
Danke.
Claudia
Zuletzt bearbeitet von Claudini95 am 14. Jan 2016 08:41, insgesamt einmal bearbeitet |
|
 |
|