| Autor |
Nachricht |
Aries123
Anmeldungsdatum: 13.12.2017
Beiträge: 1
|
 Aries123 Verfasst am: 13. Dez 2017 11:58 Titel: Kräfte auf Auflager |
 |
|
Meine Frage:
Guten Tag liebes Forum,
ich hoffe Ihr könnt mir helfen denn ich habe eine Frage zum Fachgebiet der Dynamik.
Man nehme eine Antriebswelle welche mit einem Los- und einem Festlager gelagert ist. Links an der Antriebswelle befindet sich eine Scheibe welche eine Drehzahl von 1500 1/min hat bei einem Durchmesser von Xmm.
Nun soll das ganz System im betrieb um 45grad geneigt werden.
Könnt ihr mir beantworten wie die Momente heißen, welche auf die Auflager wirken und wie ich diese berechnen kann?
Danke für die Hilfe
Meine Ideen:
Ich habe herausgefunden das das Moment, welches entsteht, versucht die Drehachse in Ihrer Position zu halten. Außerdem sind die wirkenden Kräfte abhängig von der Geschwindigkeit der Positionsänderung und der Drehzahl der Schwungscheibe.
Finde nur leider keine Formel die diese Parameter beinhaltet.
|
|
 |
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5866
Wohnort: jwd
|
| Mathefix Verfasst am: 13. Dez 2017 14:32 Titel: |
|
|
1. Dynamisches Moment
Die Schwungscheibe mit Welle wirkt wie ein Kreisel und erzeugt ein senkrecht auf der Kipprichtung stehendes Moment
a = Abstand des Massenschwerpunkts von Scheibe und Welle vom Auflagerpunkt.
2. Statische Momente
Die Statischen Momente ergeben sich aus den Gewichtskräften und deren Abstand von den Lagerpunkten.
3. Kräfte
Die axial und senkrecht auf die Lager wirkenden Kräfte werden ermittelt aus
Summe der Kräfte = 0
Summe der Momente =0
Mach eine Skizze mit allen maßen und trage die Kräfte und Momente ein.
|
|
|
Frankx
Anmeldungsdatum: 04.03.2015
Beiträge: 982
|
| Frankx Verfasst am: 13. Dez 2017 16:49 Titel: |
|
|
| Mathefix hat Folgendes geschrieben: | 1. Dynamisches Moment
Die Schwungscheibe mit Welle wirkt wie ein Kreisel und erzeugt ein senkrecht auf der Kipprichtung stehendes Moment
a = Abstand des Massenschwerpunkts von Scheibe und Welle vom Auflagerpunkt.
|
Das kann imho so schon von den Einheiten her nicht stimmen.
Die Formel sollte wenigstens die beiden Winkelgeschwindigkeiten enthalten. Abstand a, Masse m und Erdbeschleunigung g haben dafür im dynamischen Moment (Kreiselmoment) nichts verloren.
.
|
|
|
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5866
Wohnort: jwd
|
| Mathefix Verfasst am: 13. Dez 2017 18:09 Titel: |
|
|
| Frankx hat Folgendes geschrieben: | | Mathefix hat Folgendes geschrieben: | 1. Dynamisches Moment
Die Schwungscheibe mit Welle wirkt wie ein Kreisel und erzeugt ein senkrecht auf der Kipprichtung stehendes Moment
a = Abstand des Massenschwerpunkts von Scheibe und Welle vom Auflagerpunkt.
|
Das kann imho so schon von den Einheiten her nicht stimmen.
Die Formel sollte wenigstens die beiden Winkelgeschwindigkeiten enthalten. Abstand a, Masse m und Erdbeschleunigung g haben dafür im dynamischen Moment (Kreiselmoment) nichts verloren.
. |
Du hast recht! Da war mir was bei cut and paste verlorengegangen
 }{I\cdot \omega } \cdot a)
L = Drehimpuls
|
|
|
Frankx
Anmeldungsdatum: 04.03.2015
Beiträge: 982
|
| Frankx Verfasst am: 13. Dez 2017 19:23 Titel: |
|
|
| Zitat: | Man nehme eine Antriebswelle welche mit einem Los- und einem Festlager gelagert ist. Links an der Antriebswelle befindet sich eine Scheibe welche eine Drehzahl von 1500 1/min hat bei einem Durchmesser von Xmm.
Nun soll das ganz System im betrieb um 45grad geneigt werden. |
Die Lager nehmen die quasistatischen Kräfte und Momente resultierend aus der momentanen Lage des Kreiselschwerpunktes auf.
Zusätzlich wird am Kreiselschwerpunkt ein von Drehzahl und Schwenkgeschwindigkeit abhängiges Moment erzeugt.
Dieses am Kreiselschwerpunkt wirkende Moment wird über die Eulerschen Kreiselgleichungen berechnet.
Die Wirkung auf die Lager entspricht dann der Wirkung eines entsprechendem zusätzlichem, im Kreiselschwerpunkt angreifendem, Momentes.
Wenn die Schwenkbewegung mit konstanter Winkelgeschwindigkeit erfolgt, entfällt in den Eulergleichungen der Term mit den Winkelbeschleunigungen und es bleibt jeweils nur der Term mit den beiden Massenträgheitsmomenten und Winkelgeschwindigkeiten.
https://de.wikipedia.org/wiki/Eulersche_Gleichungen_(Kreiseltheorie)
.
|
|
|
Aries
Anmeldungsdatum: 13.12.2017
Beiträge: 45
|
| Aries Verfasst am: 13. Dez 2017 19:57 Titel: |
|
|
Vielen Dank schonmal für eure Hilfe 
Dann versuche ich das morgen mal zu rechnen
Willkommen im Physikerboard!
Du bist hier zweimal angemeldet, der User Aries123 wird daher demnächst gelöscht.
Viele Grüße
Steffen
|
|
|
Aries
Anmeldungsdatum: 13.12.2017
Beiträge: 45
|
| Aries Verfasst am: 18. Dez 2017 11:18 Titel: |
|
|
Habe jetzt mal die Auflager im statischen Zustand berechnet und weiß jetzt nicht genau wie das Kreiselmoment wirkt was oben beschrieben wurde.
würde gerne mein Freikörperbild hochladen doch dort kommt immer ein Error.
|
|
|
Frankx
Anmeldungsdatum: 04.03.2015
Beiträge: 982
|
| Frankx Verfasst am: 19. Dez 2017 09:15 Titel: |
|
|
| Zitat: | | Habe jetzt mal die Auflager im statischen Zustand berechnet und weiß jetzt nicht genau wie das Kreiselmoment wirkt was oben beschrieben wurde. |
Der Kreisel dreht um seine Hauptträgheitsachse.
Er wir um eine Achse, die 90° zur Hautachse steht um den Schwerpunkt , geschwenkt.
Das Kreiselmoment wirkt um die zu den beiden eben genannten Achsen senkrecht stehende dritte Achse auf den Schwerpunkt.
Alle drei Achsen bilden ein Rechtssystem. Daraus ergibt sich die Wirkrichtung des Kreiselmomentes.
Wird jedoch nicht um den Kreiselschwerpunkt, sondern um einen anderen Punkt geschwenkt, müsste imho der Steineranteil beim Schwenken berücksichtigt werden. Das Kreiselmoment müsste dann als Wirkstelle nicht den Schwerpunkt, sondern den Schwenkpunkt haben.
Die Richtung des Kreiselmomentes ist aber die gleiche.
Setzt man das berechnete Kreiselmoment nun an den Schwenkpunkt in die richtige Richtung, können die daraus wirkenden Auflagerkräfte berechnet werden.
.
|
|
|
Aries
Anmeldungsdatum: 13.12.2017
Beiträge: 45
|
| Aries Verfasst am: 21. Dez 2017 12:00 Titel: |
|
|
| Zitat: |
Setzt man das berechnete Kreiselmoment nun an den Schwenkpunkt in die richtige Richtung, können die daraus wirkenden Auflagerkräfte berechnet werden.
|
Nehmen wir an das Auflager A 100mm und Auflager B 200mm vom Schwerpunkt entfernt ist.
Sind dieses die Hebelarme um das Moment in Kräfte auf den jeweiligen Punkt umzurechnen?
|
|
|
Frankx
Anmeldungsdatum: 04.03.2015
Beiträge: 982
|
| Frankx Verfasst am: 21. Dez 2017 12:23 Titel: |
|
|
| Zitat: | | Sind dieses die Hebelarme um das Moment in Kräfte auf den jeweiligen Punkt umzurechnen? |
Wenn um den Schwerpunkt geschwenkt wird, dann ja.
Sollte der Drehpunkt der Schwenkachse an anderer Stelle liegen, muss dieser Drehpunkt (und nicht der Schwerpunkt) zur Ermittlung der Hebelarme benutzt werden. Dafür muss aber beim Kreiselmoment am Schwenkpunkt zusätzlich der Steineranteil berücksichtigt werden.
.
|
|
|
VeryApe
Anmeldungsdatum: 10.02.2008
Beiträge: 3247
|
| VeryApe Verfasst am: 22. Dez 2017 08:52 Titel: |
|
|
| Frankx hat Folgendes geschrieben: | | Sollte der Drehpunkt der Schwenkachse an anderer Stelle liegen, muss dieser Drehpunkt (und nicht der Schwerpunkt) zur Ermittlung der Hebelarme benutzt werden. Dafür muss aber beim Kreiselmoment am Schwenkpunkt zusätzlich der Steineranteil berücksichtigt werden. |
wieso sollte das so sein?
Schließlich kann ich mit konstanten Omega schwenken, dabei ist völlig egal um welchen Punkt ich schwenke, denn die winkelgeschwindigkeit um den Schwenkpunkt ist immer gleich die um den Schwerpunkt. Der einzige Unterschied besteht darin das eine Schwerpunktgeschwindigkeit vorhanden ist und diese mit einer Zentripetalkraft umgelenkt werden muß. Die zeigt aber immer auf den Schwenkpunkt und verursacht kein Kraftmoment bezüglich.
Also wieso sollte man den Steinersatz benützen beim Kreiselmoment. (Umlenkungsmoment der Rotationsgeschwindigkeiten um den Schwerpunkt)
Nicht egal ist es dann wenn ich mit verändlichen Omega schwenke.
_________________
WAS IST LOS IN EUROPA? https://www.youtube.com/watch?v=a9mduhSSC5w |
|
|
Frankx
Anmeldungsdatum: 04.03.2015
Beiträge: 982
|
| Frankx Verfasst am: 22. Dez 2017 11:31 Titel: |
|
|
| Zitat: | wieso sollte das so sein?
Schließlich kann ich mit konstanten Omega schwenken, dabei ist völlig egal um welchen Punkt ich schwenke, denn die winkelgeschwindigkeit um den Schwenkpunkt ist immer gleich die um den Schwerpunkt. |
Die 3 Eulergleichungen, wie sie in Wiki dargestellt sind, gelten nur für Schwenken um die Hauptträgheitsachsen, also um Achsen durch den Schwerpunkt.
Zitat Wiki: "In dem mit dem Körper rotierenden Hauptachsensystem lauten die eulerschen Kreiselgleichungen..."
Wenn dies nicht gegeben ist, muss imho ein entsprechender Steineranteil berücksichtigt werden.
(Wenn die Schwenkachsen nicht parallel zu den Hauptträgheitsachsen liegen, wird es noch komplizierter.)
Bei der in der Aufgabenstellung dargestellten Situation würden im Hauptträgheitsachsensystem zwei der drei Trägheitswerte identisch sein, weil der Kreisel rotationssymmetrisch ist.
Wenn aber eine Schwenkachse mit Abstand x zum Schwerpunkt betrachtet werden soll, sind die beiden Werte nicht mehr identisch (Steineranteil) und müssen entsprechend berücksichtigt werden.
Wird z.B. um die erste Achse (siehe Wiki) geschwenkt, spielt der Steineranteil für M1 nur dann eine Rolle, wenn nicht mit konstanter Schwenkgeschwindigkeit gearbeitet wird. (Das ist es, was du gemeint hast.)
Dieser Wert M1 ist dann für das notwendige Schwenkmoment und einer dazu gehörigen Lagerreaktion entscheidend. Bei konstanter Schwenkgeschwindigkeit wird M1 hier Null, da beide Terme jeweils einen Faktor Null beinhalten und ergibt damit keine Lagerreaktion.
Für M2 und M3 muss er (der Steineranteil) dann jedoch trotzdem berücksichtigt werden (,wobei einer der beiden Werte (M2 oder M3 je nach Definition der Achsen ebenfalls Null wird). Der nicht zu Null werdende Wert ist aber für eine entsprechende zusätzliche Lagerreaktion verantwortlich.
.
|
|
|
VeryApe
Anmeldungsdatum: 10.02.2008
Beiträge: 3247
|
| VeryApe Verfasst am: 22. Dez 2017 14:05 Titel: |
|
|
ich fürchte ohne Skizze sagt mir der ganze Text nicht wirklich viel. Von welcher Grafik redest du. bitte wiki link.
Den Steinerverschiebesatz verwende ich dann wenn aufgrund der Rotatorik um den Schwenkpunkt Kräfte im Schwerpunkt resultieren, die den Schwerpunkt beschleunigen und zwar nicht radial (ZEntripetalkraft) sondern tangential.
und zwar so beschleunigen das der Körper um den Schwenkpunkt dreht, weil dann ist das ganze gekoppelt und ich kann den verschiebesatz verwenden.
Bei der geschilderten Anordnung sehe ich noch nicht ganz wieso ich den verwenden sollte.
_________________
WAS IST LOS IN EUROPA? https://www.youtube.com/watch?v=a9mduhSSC5w |
|
|
Frankx
Anmeldungsdatum: 04.03.2015
Beiträge: 982
|
| Frankx Verfasst am: 22. Dez 2017 14:50 Titel: |
|
|
| Zitat: | | Von welcher Grafik redest du. bitte wiki link. |
Ich habe mich nicht auf eine Grafik bezogen, sondern auf die 3 Eulergleichungen, wobei ich eben Achse 1 als Schwenkachse betrachtet habe.
Nehmen wir Achse 2 als Hauptrotationsachse des Kreisels und Kreiseldrehzahl (Omega2)=konst. sowie Schwenkgeschwindigkeit (Omega1)=konst. (sowie Omega3=0) ergeben sich für
edit:
Eulergleichungen mit Schwenkachse parallel zu Hauptachse 1 und Achsabstand>Null.
Ende edit
M1=(J1+Steiner)*0+(J3-J2)*Omega2*0=0
M2=J2*0+((J1+Steiner)-J3)*0*Omega1=0
M3=J3*0+(J2-(J1+Steiner))*Omega2*Omega1
In Gleichung 1 ergibt sich das notwendige (Antriebs-)Moment zum Schwenken. Es ist nur dann ungleich Null (und erzeugt eine Lagerreaktion), wenn die Schwenkgeschwindigkeit nicht konstant ist.
Die Gleichung 3 ergibt einen Wert ungleich Null. In ihr ist der Steineranteil ebenfalls zu berücksichtigen. Das Moment erzeugt eine Lagerreaktion.
.
|
|
|
VeryApe
Anmeldungsdatum: 10.02.2008
Beiträge: 3247
|
| VeryApe Verfasst am: 22. Dez 2017 16:15 Titel: |
|
|
| Zitat: |
ich habe mich nicht auf eine Grafik bezogen, sondern auf die 3 Eulergleichungen, wobei ich eben Achse 1 als Schwenkachse betrachtet habe.
Nehmen wir Achse 2 als Hauptrotationsachse des Kreisels und Kreiseldrehzahl (Omega2)=konst. sowie Schwenkgeschwindigkeit (Omega1)=konst. (sowie Omega3=0) ergeben sich für
|
Im Prinzip sowie ein gewichtsloses Velorad, das um einen Aufhängepunkt kreist, der ausserhalb des Massenmittelpunkts liegt oder? und diese Umkreisung können wir als Schwenkbewegung auffassen oder?
Hier wird der Schwerpunkt aber nur radial beschleunigt zum Aufhängepunkt, da braucht man keinen Steiner bei konstanten omega, würdest du hier auch nen Steiner verwenden?
https://de.wikipedia.org/wiki/Eulersche_Gleichungen_%28Kreiseltheorie%29
| wiki hat Folgendes geschrieben: | | I1,2,3: Hauptträgheitsmomente um den Massenmittelpunkt |
_________________
WAS IST LOS IN EUROPA? https://www.youtube.com/watch?v=a9mduhSSC5w |
|
|
Frankx
Anmeldungsdatum: 04.03.2015
Beiträge: 982
|
| Frankx Verfasst am: 22. Dez 2017 18:30 Titel: |
|
|
| Zitat: | | Hier wird der Schwerpunkt aber nur radial beschleunigt zum Aufhängepunkt, da braucht man keinen Steiner bei konstanten omega, würdest du hier auch nen Steiner verwenden? |
Ich kann mir das gerade nicht wirklich vorstellen.
Im Zweifelsfall einfach bei allen Achsen, die nicht durch den Schwerpunkt gehen, den passenden Steiner mit ansetzen. Für manche Fälle (siehe oben M1) spielt er dann einfach keine Rolle, weil irgendwo noch ein Faktor Null dabei ist.
.
|
|
|
VeryApe
Anmeldungsdatum: 10.02.2008
Beiträge: 3247
|
| VeryApe Verfasst am: 22. Dez 2017 23:28 Titel: |
|
|
ich meine so etwas wie das unten dargestellte Foto.
Es besteht kein Unterschied ob die Drehachse der Welle durch den Massenmittelpunkt oder die Welle weiter nachaussen verschoben wird.
Bei konstanten omega um die vertikale Achse gibt es nur eine radiale Beschleunigung, die Zentripetalkraft im Massenmittelpunkt.
Den Steiner kann man sich dann schenken wenn im Schwerpunkt keine tangentiale Beschleunigung wirkt
Ich bin schon draufgekommen, daß du wenn du von Beschleunigungen sprichst die Terme in den Euler Kreiselgleichungen meinst. Das sind aber Beschleunigungen in mit dem Haupträgheitsachsen mitrotierten System- > beschleunigtes Bezugssystem.
Ich meinte Inertialsystem.
Dein Beispiel ist auch nicht gleichwertig meinem Beispiel wie ich zuerst gedacht haate, Bei meinen Beispiel würde bei den Haupträgheitsachsen mitrotierten System Winkelbeschleunigungen herrschen.
| Beschreibung: |
|
| Dateigröße: |
10.35 KB |
| Angeschaut: |
7043 mal |
|
_________________
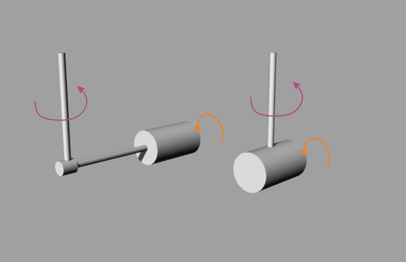
WAS IST LOS IN EUROPA? https://www.youtube.com/watch?v=a9mduhSSC5w |
|
|
Frankx
Anmeldungsdatum: 04.03.2015
Beiträge: 982
|
| Frankx Verfasst am: 23. Dez 2017 18:51 Titel: |
|
|
Für die beiden farbig gekennzeichneten Achsen dürfte es für die Momente egal sein, ob der Steiner mit angesetzt wird, sofern keine Winkelbeschleunigungen vorhanden sind.
Für die dritte Achse (in den Skizzen nicht gekennzeichnet) macht es imho beim Moment und damit bei der Lagerreaktion einen Unterschied.
Hier sollte der Steiner für die Schwenkbewegung mit berücksichtigt werden.
Hiermit verabschiede ich mich erst mal in die Feiertage.
Also bis demnächst.
.
|
|
|
VeryApe
Anmeldungsdatum: 10.02.2008
Beiträge: 3247
|
| VeryApe Verfasst am: 26. Dez 2017 20:25 Titel: |
|
|
| Zitat: | | Für die dritte Achse (in den Skizzen nicht gekennzeichnet) macht es imho beim Moment und damit bei der Lagerreaktion einen Unterschied. |
Ich habe das nicht eingezeichnet, weil ja bei den Beispiel omega 3 null sein soll.
Wenn ich jetzt um den obersten Punkt der senkrechten Achse auch noch um die dritte Achse drehe, dann macht es m.E. auch einen Unterschied.
Dann habe ich aber auch tangentiale Beschleunigungen (Inertialsystem) auf den Bezugspunkt
| Zitat: | Hier sollte der Steiner für die Schwenkbewegung mit berücksichtigt werden.
|
sehe ich auch so
_________________
WAS IST LOS IN EUROPA? https://www.youtube.com/watch?v=a9mduhSSC5w |
|
|
Aries
Anmeldungsdatum: 13.12.2017
Beiträge: 45
|
| Aries Verfasst am: 30. Dez 2017 09:53 Titel: |
|
|
Ich habe jetzt mal den Schwerpunkt ermittelt und den Drehpunkt in einer Skizze eingezeichnet. Außerdem die Auflager im statischen Zustand ohne das Kreiselmoment berechnet.
Um sich das vorzustellen habe ich hier einen Link wo ihr euch das mal angucken könnt. https://www.dropbox.com/sh/hcuelpf4morqlnk/AACdF_8lvNZo2RDjrvm05gLZa?dl=0
Durch eure Erklärungen weiß ich nun wie das Moment wirkt doch bräuchte nochmal Hilfe mit der Formel.
Ist die Formel richtig? muss nicht noch die Drehzahl des Kreisels mit einbezogen werden?
|
|
|
VeryApe
Anmeldungsdatum: 10.02.2008
Beiträge: 3247
|
| VeryApe Verfasst am: 30. Dez 2017 22:46 Titel: |
|
|
Der Drehimpulssatz ohne dalembertsche Grössen auf einen Bezugspunkt lautet
 = dL_{MP}/dt )
die Gravitationskraft samt deren Abstand zum Bezugspunkt steht eigentlich auf der linken Seite. auf der rechten Seite steht die Umlenkung des Drehimpulses. Dieser ereignet sich aufgrund von Beschleunigungen der einzelnen Massepunkte.
Vermutlich ist es dir nicht bewußt, aber du mußt Rotationsgeschwindigkeiten um eine Achse genauso umlenken wie Schwerpunktsgeschwindigkeiten (Zentripetalbeschleunigungen /kraft), wenn du die Welle samt scheibe drehst
Wie groß ist der Drehimpuls bzw zeichne ihn doch mal in den verschiedenen Situation (gerade geneigt) ein und wie ist seine zeitliche Änderung?
_________________
WAS IST LOS IN EUROPA? https://www.youtube.com/watch?v=a9mduhSSC5w |
|
|
Aries
Anmeldungsdatum: 13.12.2017
Beiträge: 45
|
| Aries Verfasst am: 31. Dez 2017 16:57 Titel: |
|
|
Als Drehimpuls (Drall) habe ich jetzt noch die Formel
Drehimpuls=Massenträgheitsmoment * Winkelgeschwindigkeit
Jedoch bin ich mit der ganzen Formel für das Kreiselmoment noch nicht so im reinen weil wenn ich jetzt zb. ein Massenschwungrad an einer Bohrmaschine laufen lasse und dieses ganze system um 45 grad schwenke merke ich das die Kraft in Abhängigkeit zur Drehzahl des Massenrads arbeitet.
doch in der Formel für das Moment befindet sich keine Drehzahl sondern nur eine Winkelgeschwindigkeit welche aber nur abhängig von dem Neigungsprozess ist.
ich möchte ja quasi die maximal Kräfte berechnen welche auf die Auflagerung der Bohrmaschine wirken und diese sind ja während des schwenken maximal.[/latex]
|
|
|
VeryApe
Anmeldungsdatum: 10.02.2008
Beiträge: 3247
|
| VeryApe Verfasst am: 01. Jan 2018 12:14 Titel: |
|
|
| Zitat: |
Drehimpuls=Massenträgheitsmoment * Winkelgeschwindigkeit |
okay, das ist ja schon mal was.
Welche Komponeten gibts denn. Du hast praktisch eine Drehung um die Schwerpunktsachse (Rotation um die Längsachse der Welle) und eine zweite Drehung um die Querachse der Welle im Lagerpunkt. Also haben wir zwei Drehimpulskomponenten.
-> einzeichnen. zeichne das doch mal.
und dann zeichne das gleiche wenn die Welle sich um ein Stück geneigt hat. wie stehen dann die Drehimpulskomponenten.
Kannsd du das?
| Zitat: | edoch bin ich mit der ganzen Formel für das Kreiselmoment noch nicht so im reinen weil wenn ich jetzt zb. ein Massenschwungrad an einer Bohrmaschine laufen lasse und dieses ganze system um 45 grad schwenke merke ich das die Kraft in Abhängigkeit zur Drehzahl des Massenrads arbeitet.
|
Die wollen wir uns doch jetzt erstmal erarbeiten, aber dabei sei jetzt mal dahingestellt was du genau als Kreiselmoment ansiehst, Jetzt gehts mal darum welches resultierende Moment auf das ganze System wirken muß, damit du die Anordnung gewünscht verdrehen kannsd.
| Zitat: |
och in der Formel für das Moment befindet sich keine Drehzahl sondern nur eine Winkelgeschwindigkeit welche aber nur abhängig von dem Neigungsprozess ist. |
Im Moment müssen beide winkelgeschwindigkeit als die der Neigung und die der Eigenrotation vorkommen, das wollen wir uns erarbeiten, aber dazu müsstest du mal die Drehimpulse einzeichnen und vergiss mal die Formel von Mathefix. Was er da ausrechnet verstehe ich selber nicht.
| Zitat: |
ich möchte ja quasi die maximal Kräfte berechnen welche auf die Auflagerung der Bohrmaschine wirken und diese sind ja während des schwenken maximal. |
mir ist klar was du willsd.
_________________
WAS IST LOS IN EUROPA? https://www.youtube.com/watch?v=a9mduhSSC5w |
|
|
Aries
Anmeldungsdatum: 13.12.2017
Beiträge: 45
|
|
|
Aries
Anmeldungsdatum: 13.12.2017
Beiträge: 45
|
| Aries Verfasst am: 02. Jan 2018 09:32 Titel: |
|
|
als nächstes stellt sich die Frage bezüglich des Massenträgheitsmoment der beiden Rotationen.
Einmal haben wir die Welle mit angeflanschter Schwungscheibe, welche um die Symmetrieachse ( X-Achse) rotiert. Da diese Achse auch durch den Schwerpunkt verläuft würde ich J1 und J2 einfach addieren.
Weiter geht es mit der Rotation um die Querachse (Y-Achse) diese sitzt außerhalb des Schwerpunktes. +(J2y+Steiner))
Steiner = Masse*Abstand zum Schwerpunkt^2
Richtig?
|
|
|
VeryApe
Anmeldungsdatum: 10.02.2008
Beiträge: 3247
|
| VeryApe Verfasst am: 02. Jan 2018 17:21 Titel: |
|
|
| Zitat: | | ich habe jetzt nochmal eine weiter Skizze hochgeladen wenn du das so meinst |
Ich meinte eigentlich einen Drehimpulsvektor pro Komponente den du einzeichnest sollst, schon mal was davon gehört.
Wenn du die rechte Hand nimmst, alle Finger geschlossen den Daumen hoch.
Dann gibt der Daumen die Richtung des Drehimpulsvektors an und die geschlossenen Finger zeigen an in welche Richtung die Drehung erfolgt.
| Zitat: |
Einmal haben wir die Welle mit angeflanschter Schwungscheibe, welche um die Symmetrieachse ( X-Achse) rotiert. Da diese Achse auch durch den Schwerpunkt verläuft würde ich J1 und J2 einfach addieren.
|
okay
| Zitat: |
Weiter geht es mit der Rotation um die Querachse (Y-Achse) diese sitzt außerhalb des Schwerpunktes.
|
das ist zwar richtig mit Steiner, aber das brauchst du nicht, das wirsd du sehen wenn die Drehimpulskomponenten (vektor ) einzeichnest.
einmal in der geraden Lage und dann ein kleines bisschen verdreht.
Ich kann momentan nicht zeichnen ich muß das Vorzimmer fertig machen.
Das dauert zulange, das Zeichnen.
_________________
WAS IST LOS IN EUROPA? https://www.youtube.com/watch?v=a9mduhSSC5w |
|
|
Aries
Anmeldungsdatum: 13.12.2017
Beiträge: 45
|
| Aries Verfasst am: 02. Jan 2018 20:06 Titel: |
|
|
Ich habe dann nochmal eine neue Skizze eingezeichnet und mich versucht im 3D Bereich auszudrücken
http://www.dropbox.com/sh/hcuelpf4morqlnk/AACdF_8lvNZo2RDjrvm05gLZa?dl=0
Die Rot eingezeichneten Pfeile auf den jeweiligen Achsen soll der Drehimpuls sein wenn ich das richtig verstanden habe.
Ich habe nun erfahren das der Drehimpuls etwas über die "Wucht" einer Drehbewegung aussagt, doch wie bekommt man daraus die Kraft welche auf die Auflager wirkt.
|
|
|
VeryApe
Anmeldungsdatum: 10.02.2008
Beiträge: 3247
|
| VeryApe Verfasst am: 02. Jan 2018 21:08 Titel: |
|
|
| Zitat: | | Die Rot eingezeichneten Pfeile auf den jeweiligen Achsen soll der Drehimpuls sein wenn ich das richtig verstanden habe. |
genau.
Wenn du jetzt die Drehimpulskomponente anschaust die du bei der Scheibe eingezeichnet hast also auf der x Achse.
die steht doch nacher, wenn die Welle schräg steht in einer völlig anderen Richtung, das hast du leider nicht eingezeichnet, du hast sie nur eingezeichnet wenn die Welle horizontal steht.
Die Drehimpulskomponente die in z Richtung zeigt bleibt auch nach der Schrägstellung gleich, ist dir klar warum?
Der Drehimpuls in x Richtung steht stellvertretend für die Rotationsgeschwindigkeiten der einzelnen Massepunkte, diese müssen nach der Schrägstellung ganz anders im Raum rotieren, weil die Drehachse ganz anders liegt, das verursacht unser Drehmoment. dL/dt der Drehimpuls ändert sich.
Der Drehimpuls in z Richtung ändert sich nicht denn die Drehachse verändert sich ja nicht. und das Trägheitsmoment bleibt auch gleich, die rotieren um dieselbe Achse wie vorher.
| Zitat: | Ich habe nun erfahren das der Drehimpuls etwas über die "Wucht" einer Drehbewegung aussagt, doch wie bekommt man daraus die Kraft welche auf die Auflager wirkt.
|
über den Drallsatz in der Kombination mit dem dynamischen Grundgesetz
plus
 bzw allgeimein 
wie bei jeden Mechanik problem.
Jetzt habe ich doch noch schnell was gezeichnet.
Stell dir eine unendlich kleine Umlenkung vor also ein kurzer Zeitausschnitt in der sich die Achse um  verlagert.
Wie würdest du dL berechnen. als vergleich dazu habe ich links die änderung einer Schwerpunktsgeschwindigkeit gezeichnet, auch hier müssen wir das dv ermitteln um dann auf die Zentripetalbeschleunigung zu kommen und so die Kraft zu ermitteln, Bei der Herleitung der ZEntripetalbeschleunigung ist es das gleiche, nur die Vektoren stehen tangential, beim Drehimpuls hier wäre es radial, aber die gleiche vorgehensweise.
kannsd du das dL ermitteln? bzw hast du schon mal probiert die Zentripetalbeschleunigung herzuleiten.
| Beschreibung: |
|
| Dateigröße: |
6.49 KB |
| Angeschaut: |
6795 mal |
|
_________________
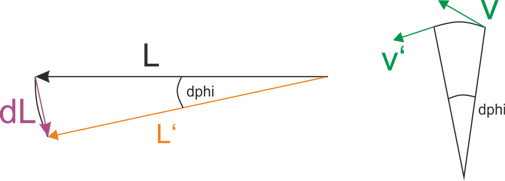
WAS IST LOS IN EUROPA? https://www.youtube.com/watch?v=a9mduhSSC5w
Zuletzt bearbeitet von VeryApe am 02. Jan 2018 21:30, insgesamt einmal bearbeitet |
|
|
VeryApe
Anmeldungsdatum: 10.02.2008
Beiträge: 3247
|
| VeryApe Verfasst am: 02. Jan 2018 21:19 Titel: |
|
|
folgendes. Das sich der Drehimpuls in z nicht ändert, stimmt natürlich nur, wenn wir davon ausgehen das wir mit einer konstanten winkelgeschwindigkeit um die zAchse drehen. In wirklichkeit mußt du ja die ganze Anordnung erst aus den Stillstand beschleunigen und dann wieder abbremsen, dann würde sich natürlich auch der Drehimpuls in z verändern.
wenn wir davon ausgehen das wir nicht winkelbeschleunigen um z dann bleibt er gleich, und wir brauchen keinen Steiner, weil wir keine Drehimpulsänderung haben, und damit ist diese Achse uninteressant.
es kommt natürlich jetzt auch darauf an was du betrachten willsd. willsd du von einem konstanten omega(z) ausgehen?
_________________
WAS IST LOS IN EUROPA? https://www.youtube.com/watch?v=a9mduhSSC5w |
|
|
Aries
Anmeldungsdatum: 13.12.2017
Beiträge: 45
|
| Aries Verfasst am: 02. Jan 2018 22:14 Titel: |
|
|
| VeryApe hat Folgendes geschrieben: |
es kommt natürlich jetzt auch darauf an was du betrachten willsd. willsd du von einem konstanten omega(z) ausgehen? |
Es soll der Fall betrachtet werden, bei dem die Lager am meisten belastet werden.
Und das wird der Fall sein wenn beschleunigt oder verzögert wird.
Bezüglich dL und der Drallsatz das gucke ich mir morgen an.
|
|
|
VeryApe
Anmeldungsdatum: 10.02.2008
Beiträge: 3247
|
| VeryApe Verfasst am: 02. Jan 2018 22:21 Titel: |
|
|
ohne eine Vorgabe einer Beschleunigung was willsd da ausrechnen, je nach Beschleunigungsstärke steigen die Kräfte ins unermessliche, das wäre völlig sinnlose Aufgabenstellung.
Beispiel: Ich soll den Fall ausrechnen bei dem das Auto am meisten belastet wird, das ist der Fall bei dem die Beschleunigung am größen ist.
_________________
WAS IST LOS IN EUROPA? https://www.youtube.com/watch?v=a9mduhSSC5w |
|
|
Aries
Anmeldungsdatum: 13.12.2017
Beiträge: 45
|
| Aries Verfasst am: 03. Jan 2018 07:58 Titel: |
|
|
|
Ich habe die Zeit (1 Sekunde) gegeben wie lange das Schwenken aus der horizontalen bis auf 60° dauert. Wird dieses als konstant berechnet ? ich weiß ja nicht wie lange und auf welche Geschwindigkeit beschleunigt wird.
|
|
|
VeryApe
Anmeldungsdatum: 10.02.2008
Beiträge: 3247
|
| VeryApe Verfasst am: 03. Jan 2018 23:22 Titel: |
|
|
es gibt die Möglichkeit man beschleunigt (winkelbeschleunigung) dann fährt man konstant und dann verzögert man wieder. Es gibt die Möglichkeit man beschleunigt und verzögert ohne konstante Phase, und das symetrisch oder nicht symetrisch also einer der Phasen ist länger die Beschleunigung der einzelnen Phasen wäre dann unterschiedlich,
Mit dieser Angabe gibt es unendlich viele Variationen. Ich kann dir da nicht weiterhelfen, wenn du selber nicht weißt was du ausrechnen willsd.
Fürs begreifen wäre sicher mal einfacher davon auszugehen das omega(z) mal konstant ist.
_________________
WAS IST LOS IN EUROPA? https://www.youtube.com/watch?v=a9mduhSSC5w |
|
|
Aries
Anmeldungsdatum: 13.12.2017
Beiträge: 45
|
| Aries Verfasst am: 04. Jan 2018 08:15 Titel: |
|
|
| VeryApe hat Folgendes geschrieben: | es gibt die Möglichkeit man beschleunigt (winkelbeschleunigung) dann fährt man konstant und dann verzögert man wieder. Es gibt die Möglichkeit man beschleunigt und verzögert ohne konstante Phase, und das symetrisch oder nicht symetrisch also einer der Phasen ist länger die Beschleunigung der einzelnen Phasen wäre dann unterschiedlich,
|
Was wird denn alles benötigt um es so zu berechnen das symmetrisch beschleunigt und verzögert wird?
| VeryApe hat Folgendes geschrieben: |
Fürs begreifen wäre sicher mal einfacher davon auszugehen das omega(z) mal konstant ist. |
Dann würde ich sagen ich versuche das erstmal mit omega(z) = konstant.
Bezüglich des Drallsatzes  bin ich nicht wirklich weiter gekommen die meisten Erklärungen beziehen sich auf Vektoren und ich habe ja Parameter mit denen ich rechnen kann.
http://me-lrt.de/a51-ableitung-drehimpuls-drehmoment
oder rechne ich das System mit Vektoren?
Wie werden die Wirkenden kräfte berechnet wenn wir die Momente aus dem Drallsatz besitzen?
Wir haben ja dann 3 Momente anliegen 2 aus der Rotationsbewegung der Schwungmasse und 1 aus der Rotationsbewegung der Verstellung.
das zweite Moment bezüglich der Rotationsbewegung der Schwungmasse steht nach der Schwenkbewegung ja anders im raum.
|
|
|
VeryApe
Anmeldungsdatum: 10.02.2008
Beiträge: 3247
|
| VeryApe Verfasst am: 04. Jan 2018 12:41 Titel: |
|
|
| Zitat: | | Was wird denn alles benötigt um es so zu berechnen das symmetrisch beschleunigt und verzögert wird? |
na wenn du mal festlegst das beide Phasen symmetrisch seien und durgehend sind (keine konstante Phase) dann brauchst du nur noch angeben wie weit du insgesamt drehen willsd. und mit der Kombination bei 60 Grad 1 Sek ist dann alles festgelegt.
| Zitat: | | Bezüglich des Drallsatzes bin ich nicht wirklich weiter gekommen die meisten Erklärungen beziehen sich auf Vektoren und ich habe ja Parameter mit denen ich rechnen kann. |
Winkel- / Beschleunigung, Kräfte/Momente, Winkel- / Geschwindigkeiten, Dreh-/ Impuls.
Alles sind Vektoren und das du 3 Dimension brauchst hast du selbst schon gesehen, weil du schon 3d hingezeichnet hast, insofern verstehe ich deine Frage nicht.
Du kannsd alles in 2d Schnitten ganz normal berechnen, und mußt ned unbedingt in Vekorschreibweise lösen, aber trotzdem sind ja alles Vektoren, auch wenn ich mit den einzelnen Komponenten rechne.
| Zitat: |
Wie werden die Wirkenden kräfte berechnet wenn wir die Momente aus dem Drallsatz besitzen?
Wir haben ja dann 3 Momente anliegen 2 aus der Rotationsbewegung der Schwungmasse und 1 aus der Rotationsbewegung der Verstellun |
und dabei ist noch gar nicht geklärt wie das Moment der Verstellung aufgebracht wird. also das Moment das system beschleunigt und wieder verzögert. Wenn ich das zum Beispiel mit einer Hand drehe, belastet das Moment selbst das Lager. Wenn ich selbst mit 2 Händen drehe als Kräftepaar dann ist die Lagerung unbelastet.
Insgesamt frage ich mich aber, für was du das brauchst,
Hast du überhaupt Mechanik?
 und  ist doch die Grundbasis der Mechanik für jeden Riss
Mir erscheints jetzt so als hättest du wenig Ahnung von Mechanik, dann möchte ich mich aber ausklincken, weil dann kommen wir von einem Problem zum nächsten Problem bei den Erklärungen und zum SChluss kann ich alles selber rechnen, das kenn ich schon.
_________________
WAS IST LOS IN EUROPA? https://www.youtube.com/watch?v=a9mduhSSC5w |
|
|
Aries
Anmeldungsdatum: 13.12.2017
Beiträge: 45
|
| Aries Verfasst am: 05. Jan 2018 19:59 Titel: |
|
|
[quote="VeryApe"] | Zitat: |
| Zitat: | | Bezüglich des Drallsatzes bin ich nicht wirklich weiter gekommen die meisten Erklärungen beziehen sich auf Vektoren und ich habe ja Parameter mit denen ich rechnen kann. |
Winkel- / Beschleunigung, Kräfte/Momente, Winkel- / Geschwindigkeiten, Dreh-/ Impuls.
Alles sind Vektoren und das du 3 Dimension brauchst hast du selbst schon gesehen, weil du schon 3d hingezeichnet hast, insofern verstehe ich deine Frage nicht. |
Damit meinte ich die Vektorschreibweise also die Berechnung über das Kreuzprodukt aber wie du schon sagst lässt sich das auch ohne Vektorschreibweise rechnen.
wie die Kräfte wirken also summe der Kräfte und Momente krieg ich auch hin
Was für mich jetzt noch Unklar ist, ist die Sache mit dem Drall
gehen wir davon aus ich habe einen Drehimpuls mit 
sprich Drehimpuls=Massenträgheitsmoment*Winkelgeschwindigkeit.
als Ergebnis bekomme ich bsp. L = 150 kg*m^2 / s
Wenn ich das nun über die zeit ableite komm ich auf  -150 kg*m^2 / s^2
Welches das Moment von -150Nm ergibt.
soweit richtig?
Doch wie wirkt dieses Moment also um welchen Punkt. weil ein Moment um einem Punkt wirkt bei dem eine Kraft auf einen Hebelarm wirkt 
Weil so wie ich es eingezeichnet habe wirkt der Drehimpuls in entlang der Drehachse doch was passiert nach der Ableitung? Was kann ich als Punkt ansehen worum das Moment wirkt.
Wirkt es nun um die rotierende Masse?[/latex]
|
|
|
VeryApe
Anmeldungsdatum: 10.02.2008
Beiträge: 3247
|
| VeryApe Verfasst am: 05. Jan 2018 20:39 Titel: |
|
|
bezüglich deiner privaten Nachricht. Ich bin durchaus gewillt zu helfen, ich wollte nur vorher abchecken, ob das überhaupt einen Sinn hat, oder ob man da bis auf die Grundbasis der Mechanik zurückgehen muß, dazu habe ich momentan keinen Nerv. Weil dann kommt eine Erklärung und in dieser Erklärung wird wieder was anderes nicht verstanden, dann versucht man das zu erklären und dann gibts wieder etwas anderes was nicht verstanden wird, das geht dann so weiter und zum Schluss rechnet man selber, weil sonst geht das weiter bis zur Grundbasis zurück.
Das mit der Vektorschreibweise liegt mir selber auch nicht.
Zumindest hast du schon mal Summe aller Kräfte und Momente in diversen Mechanikbeispielen mit den einzelnen Komponenten angewendet oder=?
also in der Statik:
Die Mz Momente wären dann alle Momente die um z Achsen drehen also Fx*y und Fy*x-
In unserem Fall haben wir halt nicht ausschließlich null Gleichsetzungen weil wir in diversen Rissen resultiernde Größen haben wie schwerpunktsbeschleunigungen und drehimpulsänderungen.
Also das kannsd du oder=?
| Zitat: | gehen wir davon aus ich habe einen Drehimpuls mit
sprich Drehimpuls=Massenträgheitsmoment*Winkelgeschwindigkeit.
|
sagen wir mal das wäre der Drehimpuls den du nach links wirkend eingezeichnet hast auf der Rotationsachse der Welle.
Das dL nach dt müssen wir ermitteln das L verändert sich im Raum und dann wärs halt wichtig du würdest verstehen wenn zu der Skizze zurück gehst wie du den dL Vektor da berechnest.
schau dir die Skizze nochmal an
du hast L und L' beide sind vom Betrag her gleich aber L' ist etwas schräger danach, die vektorielle Addition von dL +L ergibt L'.
wie würdest du jetzt den Betrag von dL ermitteln rein mathematisch.
stell da vor das sind 2 Kräfte A und A' und ich frage dich welchen vektor muß ich zu A hinzu addieren das ich A' erhalte.
| Zitat: | | Doch wie wirkt dieses Moment |
in Richtung des dL Vektors zu Beginn nach unten. und wenn du das rotationstechnisch übersetzen willsd wendest du wieder deine Rechte Hand mit den Daumen an.
also daumen zeigt nach unten die finger drehen im uhrzeiger sinn in den Bildschirm hinein. Das Moment dreht also in der Horizontalen Ebene im uhrzeigersinn , wenn du von oben draufschaust.
_________________
WAS IST LOS IN EUROPA? https://www.youtube.com/watch?v=a9mduhSSC5w |
|
|
Aries
Anmeldungsdatum: 13.12.2017
Beiträge: 45
|
| Aries Verfasst am: 07. Jan 2018 15:35 Titel: |
|
|
| VeryApe hat Folgendes geschrieben: |
Das mit der Vektorschreibweise liegt mir selber auch nicht.
Zumindest hast du schon mal Summe aller Kräfte und Momente in diversen Mechanikbeispielen mit den einzelnen Komponenten angewendet oder=?
also in der Statik:
Die Mz Momente wären dann alle Momente die um z Achsen drehen also Fx*y und Fy*x-
In unserem Fall haben wir halt nicht ausschließlich null Gleichsetzungen weil wir in diversen Rissen resultiernde Größen haben wie schwerpunktsbeschleunigungen und drehimpulsänderungen.
Also das kannsd du oder=? |
Ja die Kräftegleichgewicht sind bekannt.
| Zitat: |
du hast L und L' beide sind vom Betrag her gleich aber L' ist etwas schräger danach, die vektorielle Addition von dL +L ergibt L'.
wie würdest du jetzt den Betrag von dL ermitteln rein mathematisch.
stell da vor das sind 2 Kräfte A und A' und ich frage dich welchen vektor muß ich zu A hinzu addieren das ich A' erhalte. |
Wenn du sagst das dL+L=L´ist dann sollte ja L´- L = dL sein.
Dann wäre bei bleichen Betrag dL=0 oder berechnen wir L´ mit Sin(60°) durch die Winkeländerung? Jedoch bleibt die Position zur den Auflagern her gleich und nur das Gesamtsystem wird gedreht. 
| Zitat: | in Richtung des dL Vektors zu Beginn nach unten. und wenn du das rotationstechnisch übersetzen willsd wendest du wieder deine Rechte Hand mit den Daumen an.
also daumen zeigt nach unten die finger drehen im uhrzeiger sinn in den Bildschirm hinein. Das Moment dreht also in der Horizontalen Ebene im uhrzeigersinn , wenn du von oben draufschaust |
-> der Punkt von dem der Drehimpuls ausgeht, ist der Mittelpunkt um dem das Moment wirkt?
|
|
|
VeryApe
Anmeldungsdatum: 10.02.2008
Beiträge: 3247
|
| VeryApe Verfasst am: 07. Jan 2018 18:07 Titel: |
|
|
| Zitat: | Ja die Kräftegleichgewicht sind bekannt.
|
wie gesagt werden wir in einen Riss Gleichgewichte haben im anderen nicht, aber wenn du das anschreiben kannsd, dann haben wir ja schon mal die halbe Miete.
| Zitat: | Wenn du sagst das dL+L=L´ist dann sollte ja L´- L = dL sein.
|
ja mehr als ein umstellen ist das aber nicht.
und es sollte eigentlich so sein
ich dachte das wäre klar wenn du die Skizze anschaust und habs aus Bequemlichkeit nicht exakt hingeschrieben,
| Zitat: | Dann wäre bei bleichen Betrag dL=0 oder berechnen wir L´ mit Sin(60°) durch die Winkeländerung?
|
ja so gesehen wäre es null, aber so habe ich es nicht gemeint, ich dachte anhand der skizze wäre klar das ich hier eine vektoraddition meine.
und ja über die Winkeländerung, aber nicht gleich über 60 Grad sondern über eine unendlich kleine winkeländerung, wir betrachten zunächst alles unendlich klein und zeichnens aber übertrieben groß, der drehimpuls ändert sich doch über jeden Teil winkel anders im Raum, wir wollen keinen Durchschnittswertüber 60 Grad wir wollen den exakten Wert für kleine Winkeleinheit.
| Zitat: |
Jedoch bleibt die Position zur den Auflagern her gleich und nur das Gesamtsystem wird gedreht. |
aber der Drehimpuls ändert sich.
Jetzt geh mal her nimm die Skizze mit L und L'.
legt da ein Koordinatensystem rein und berechne anhand des gegeben winkels dphi die einzlenen Komponenten von dL und die nächste Frage
wie können wir denn den unendlich kleinen verdrehwinkel noch ausdrücken, wenn wir sagen dieser verdrehtwinkel entsteht über eine unendlich kleine Zeitspanne dt über der sich die Gesamtordnung verdreht.
| Zitat: |
der Punkt von dem der Drehimpuls ausgeht, ist der Mittelpunkt um dem das Moment wirkt? |
Drehimpuls ist eine Zustansgröße auf einen Bezugspunkt. Den Bezugspunkt kannsd du frei wählen und hast einen Punkt auf der Wellenachse gewählt. Moment ist eine Prozessgröße auf denselben Bezugspunkt, die gibt keinen zustand an sondern wie sich was verändert.
Das Moment kann ganz anders wirken als der Drehimpulsvekor. wenn du dir jetzt beides als Vektor vorstellt.
wichtig ist das du denselben Bezugspunkt wählst. Es gibt reine Drehmomente da ist der Bezugspunkt egal, mit dem quäl ich dich jetzt nicht.
Für Betrachtungen des Drehimpuls und des Momentes wählst du denselben Bezugspunkt, wenn du unterschiedliche verwendest wirds falsch, wähle einen und bleibe dabei, wie in der Statik!
Ich zeichne eine Skizze, daß du dir das besser vorstellen kannsd mit dem Drehimpuls und Moment wenn ich Zeit habe.
_________________
WAS IST LOS IN EUROPA? https://www.youtube.com/watch?v=a9mduhSSC5w |
|
|
Aries
Anmeldungsdatum: 13.12.2017
Beiträge: 45
|
| Aries Verfasst am: 08. Jan 2018 08:44 Titel: |
|
|
| Zitat: | Jetzt geh mal her nimm die Skizze mit L und L'.
legt da ein Koordinatensystem rein und berechne anhand des gegeben winkels dphi die einzlenen Komponenten von dL und die nächste Frage |
da habe ich mich jetzt auf dein Bild von weiter oben berufen und die Formel über den Kosinussatz aufgestellt.
 })
| Zitat: |
wie können wir denn den unendlich kleinen verdrehwinkel noch ausdrücken, wenn wir sagen dieser verdrehtwinkel entsteht über eine unendlich kleine Zeitspanne dt über der sich die Gesamtordnung verdreht. |
da würde ich jetzt sagen, das dieses abhängig ist ob wir beschleunigen oder verzögern. Sprich w0=0 oder w0>0
Denn bei w0=0
/2)
und bei w0>0
\cdot t/2)
|
|
|
|
Registrieren
Login
FAQ
Suchen
