| Autor |
Nachricht |
Porygon2
Anmeldungsdatum: 10.07.2015
Beiträge: 4
|
 Porygon2 Verfasst am: 10. Jul 2015 13:25 Titel: Formeln zum zweidimensionalen elastischen Stoß Porygon2 Verfasst am: 10. Jul 2015 13:25 Titel: Formeln zum zweidimensionalen elastischen Stoß |
 |
|
Meine Frage:
Ich benötige die Formeln für ein Programm, in dem ich Bälle (Kreise) zweidimensional kollidieren lassen will, auf dass sie sich physikalisch korrekt voneinander abstoßen. Reibung und ähnliches wird vernachlässigt, daher voll elastisch, aber wichtig sind Richtung, Masse und Geschwindigkeit.
Alle Seiten im Internet, die ich dazu besucht habe, beziehen sich immer nur auf Sonderfälle, z.B. nur eindimensional, gleiche Massen, eine Kugel in Ruhe usw. oder sind lückenhaft und schlecht erklärt. Daher brauche ich bitte eure Hilfe!
Meine Ideen:
Die Bälle haben eine feste Richtung, Masse und Geschwindigkeit und eine Kollision liegt vor, falls sie sich berühren. Eigentlich muss ich für die Kollision ja dann nur zweierlei berechnen: die neue Geschwindigkeit und die neue Richtung für jeden der zwei Bälle.
Also ich kenne die Formeln für die Geschwindigkeiten nach dem Stoß, die zumindest für eindimensionale Stöße gelten.
}{m_{1} + m_{2}})
}{m_{1} + m_{2}})
Aber die sind ja nicht ohne Weiteres für zweidimensionale Stöße gültig.
Was die neue Richtung angeht, weiß ich - weil es Kugeln sind - dass es eine Zentralsteigung gibt (eine Gerade durch die Mittelpunkte beider Kugeln) und eine Tangente durch ihren gemeinsamen Berührpunkt (senkrecht zur Zentralsteigung). Es hat also mit der Tangente zu tun, aber ich weiß nicht genau wie, denn Einfallswinkel = Ausfallswinkel gilt nicht, wenn Masse und Geschwindigkeit unterschiedlich sind.
Ich hab übrigens diese Simulation gefunden, die ziemlich genau das wiedergibt.
http://www.cornelsen.de/sites/medienelemente_cms/mel_xslt_gen/progs/html/mels/mel_351007_1.html
Weiß jemand, welche Formeln ich brauche? Ohne Hilfe komm ich jetzt leider nicht weiter und ich bin für jede dankbar.
|
|
 |
yellowfur
Moderator

Anmeldungsdatum: 30.11.2008
Beiträge: 804
|
|
 |
Porygon2
Anmeldungsdatum: 10.07.2015
Beiträge: 4
|
 Porygon2 Verfasst am: 10. Jul 2015 16:45 Titel: Porygon2 Verfasst am: 10. Jul 2015 16:45 Titel: |
 |
|
Hallo yellowfur,
Ich brauche es wie gesagt nur unter Berücksichtigung von Richtung, Masse und Geschwindigkeit, also keine Drehungen. Die Simulation hinter dem Link zeigt eigentlich, was ich brauche. Ich muss quasi die Formeln hinter der Simulation verstehen. (Der Quellcode ist ja leider geheim...)
Ich schau mir dieses andere Thema nochmal näher an, aber das scheint mir sehr auf den Drehimpuls fixiert zu sein, den ich ja nicht brauche.
Einfallswinkel = Ausfallswinkel gilt jedenfalls NICHT, das wäre nur der Fall, wenn die Kugel auf eine Wand oder unbewegbare Kugel träfe. Kann sich das andere Objekt aber auch bewegen, stimmt es nicht. Wenn ich in der besagten Simulation trotz gleichen Massen und Geschwindigkeiten einen Winkel von 45° einstelle, denn ist der Ausfallswinkel der roten Kugel nur 35° (Summe 80°). Und ich will wissen, wie man auf dieses Ergebnis kommt (exemplarisch).
https://de.wikipedia.org/wiki/Sto%C3%9F_(Physik)#Zweidimensionaler_elastischer_Sto.C3.9F
Dieser Abschnitt aus Wikipedia sah für mich zunächst nach dem aus, was ich suche. Dazu in vektorieller Form, da sind die Richtungen gleich enthalten. Leider ist er furchtbar undurchschaubar. Da steht zum Beispiel nicht, was  , ,  , ,  , ,  und und  darstellen. Und manchmal steht da einfach "obige Formel" und keiner weiß, welche gemeint ist. Ich brüte seit Tagen darüber, daher wende ich mich jetzt an ein Forum. darstellen. Und manchmal steht da einfach "obige Formel" und keiner weiß, welche gemeint ist. Ich brüte seit Tagen darüber, daher wende ich mich jetzt an ein Forum.
Also, die Ausgangssituation:
Zwei Kugeln (in 2D) berühren sich an 1 Punkt und haben beide eine Masse und einen Richtungsvektor. Der Betrag (also die Länge) des Vektors bestimmt die Geschwindigkeit. Sehe ich das richtig? Genauso das zeigt die Simulation. Ich muss also die veränderten Vektoren berechnen können. Ich bin mir sicher, dass es dafür feste Formeln gibt, nur weiß und finde ich sie nicht.

|
|
 |
DrStupid
Anmeldungsdatum: 07.10.2009
Beiträge: 5043
|
 DrStupid Verfasst am: 10. Jul 2015 19:17 Titel: DrStupid Verfasst am: 10. Jul 2015 19:17 Titel: |
 |
|
Der elastische Stoß starrer glatter Kugeln führt zu den Geschwindigkeiten

und

mit dem Kraftstoß

sowie dem Abstand

und der Geschwindigkeitsdifferenz

bei der Kollision.
|
|
 |
Porygon2
Anmeldungsdatum: 10.07.2015
Beiträge: 4
|
 Porygon2 Verfasst am: 11. Jul 2015 00:04 Titel: Porygon2 Verfasst am: 11. Jul 2015 00:04 Titel: |
 |
|
Hallo DrStupid,
vielen Dank für deine Formeln. Ich habe mit diesen ein Beispiel durchgerechnet und dann mit der Simulation verglichen. Leider kamen dabei völlig unterschiedliche Werte heraus. Mehr noch, man kann mit den von dir genannten Formeln keine Richtung bestimmen, da es keine Vektoren beinhaltet. Wenn ich in der Simulation nur den Winkel verändere, ändern sich schon die neuen Geschwindigkeiten. Daher weiß ich deine Formeln leider nicht anzuwenden, was schade ist...
http://phynformatik.de/wordpress/wp-content/uploads/2010/01/facharbeit.pdf
Ich habe diese pdf nochmal gefunden. Bei genauerem Betrachen habe ich gemerkt, dass das eigentlich das beschreibt, was ich suche. Hoffe ich zumindest, ich muss es erst noch richtig verstehen. Aber da werden die neue Richtung und Geschwindigkeit durch Vektoren berechnet, sogar in 3D das klingt vielversprechend, mal sehen.
|
|
 |
Porygon2
Anmeldungsdatum: 10.07.2015
Beiträge: 4
|
 Porygon2 Verfasst am: 12. Jul 2015 17:56 Titel: Porygon2 Verfasst am: 12. Jul 2015 17:56 Titel: |
 |
|
Ich kann stolz verkünden, dass ich die Lösung nun selbst gefunden habe und bereits erfolgreich in mein Programm integriert habe. Für die Nachwelt werde ich trotzdem noch die Formeln aufschreiben, die ich hier gerne bekommen hätte und mir bedauerlicherweise keiner nennen konnte.
Gegeben sind von Kugel 1 und Kugel 2 die Massen  und und  , ihre Mittelpunkte als Ortsvektoren , ihre Mittelpunkte als Ortsvektoren  und und  sowie die Richtungsvektoren sowie die Richtungsvektoren  und und  , deren Betrag jeweils die Geschwindigkeit der Kugel ist. Gesucht sind die neuen Richtungsvektoren , deren Betrag jeweils die Geschwindigkeit der Kugel ist. Gesucht sind die neuen Richtungsvektoren  und und  , welche die ursprünglichen ersetzen sollen. , welche die ursprünglichen ersetzen sollen.
Liegt eine Kollision vor, dann berechnet man die Gerade, die durch beide Kugelmittelpunkte läuft, als Vektor.

Die beiden 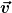 Vektoren zerlegt man jeweils in Vektoren zerlegt man jeweils in  und und  . .

(Dabei liegt  auf auf 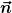 . Und . Und  orthogonal dazu.) orthogonal dazu.)
 } {\vec{n_{x}}^{2} + \vec{n_{y}}^{2}})



Dann für beide Kugeln einen Hilfsvektor  , welcher die Massen beinhaltet. , welcher die Massen beinhaltet.
}{m_{1} + m_{2}})
}{m_{1} + m_{2}})
}{m_{1} + m_{2}})
}{m_{1} + m_{2}})
Und jetzt lassen sich die endgültigen beiden Vektoren  ausrechnen und dessen Beträge. ausrechnen und dessen Beträge.

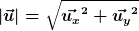
Fertig!!!
|
|
 |
NeoJones
Anmeldungsdatum: 09.04.2016
Beiträge: 6
|
 NeoJones Verfasst am: 09. Apr 2016 15:35 Titel: NeoJones Verfasst am: 09. Apr 2016 15:35 Titel: |
 |
|
Ich hätte da auch ein Problem und hoffe, das mir hier geholfen werden kann - denn entweder bin ich einfach nur dumm oder es ist sehr kompliziert.
Auf der folgenden Seite ist unter Punkt 7 die Aufgabe für einen elastischen Stoss gestellt worden. Etwas weiter unten findet man dann die Lösung zu Punkt 7:
http://wwwex.physik.uni-ulm.de/lehre/krm-2008-2009/ueb/ue05/uebungsblatt05.html
Mein Problem ist nun, den Winkel a1 auszurechnen. In der Lösung dort steht Winkel a1 = 90 - a2
was definitiv falsch sein muss. Denn wenn man die Kugel nur ganz leicht versetzt anspielen würde (b = 2mm, anstatt 12mm), würde man sehr kleine Winkel erhalten, welche deutlich unter 90 Grad liegen würden. Von daher kann die Formel doch so schonmal nicht stimmen oder??
Ich hoffe echt ihr könnte mir helfen, bin hier schon seit Stunden am suchen, lesen, rechnen.... 
Danke, gruß Olli
|
|
 |
E=mc²
Anmeldungsdatum: 24.06.2014
Beiträge: 494
|
 E=mc² Verfasst am: 09. Apr 2016 17:43 Titel: E=mc² Verfasst am: 09. Apr 2016 17:43 Titel: |
 |
|
Im ersten Posting dieses Threads hat der Fragesteller einen Link gepostet zu einem Applet für dezentrale Stöße:
| Porygon2 hat Folgendes geschrieben: | | http://www.cornelsen.de/sites/medienelemente_cms/mel_xslt_gen/progs/html/mels/mel_351007_1.html |
Stell doch mal dort eine sehr kleine Zahl für b ein und für die Geschwindigkeit der roten Kugel null. Dann schau dir an, was passiert
Ist dir klar, wie die Autoren zur Aussage alpha1=90-alpha2 gekommen ist?
|
|
 |
NeoJones
Anmeldungsdatum: 09.04.2016
Beiträge: 6
|
 NeoJones Verfasst am: 09. Apr 2016 22:54 Titel: NeoJones Verfasst am: 09. Apr 2016 22:54 Titel: |
 |
|
| E=mc² hat Folgendes geschrieben: | Stell doch mal dort eine sehr kleine Zahl für b ein und für die Geschwindigkeit der roten Kugel null. Dann schau dir an, was passiert
|
Das habe ich gemacht und genau das ist ja das, was ich meine. selbst bei ganz geringem Abstand (b=1mm) läuft die 1. Kugel doch nicht im 90 Grad Winkel von der 2. ab... !? Sie würde doch im Normalfall einen Richtungswinkel unter 10 Grad vielleicht haben, da es ja fast ein zentraler Stoss wäre. Das ist ja exakt mein Problem was ich habe.
| E=mc² hat Folgendes geschrieben: | | Ist dir klar, wie die Autoren zur Aussage alpha1=90-alpha2 gekommen ist? |
Nein, ich habe echt keine Ahnung...   
|
|
 |
E=mc²
Anmeldungsdatum: 24.06.2014
Beiträge: 494
|
 E=mc² Verfasst am: 09. Apr 2016 23:13 Titel: E=mc² Verfasst am: 09. Apr 2016 23:13 Titel: |
 |
|
| NeoJones hat Folgendes geschrieben: |
Das habe ich gemacht und genau das ist ja das, was ich meine. selbst bei ganz geringem Abstand (b=1mm) läuft die 1. Kugel doch nicht im 90 Grad Winkel von der 2. ab... !? Sie würde doch im Normalfall einen Richtungswinkel unter 10 Grad vielleicht haben, da es ja fast ein zentraler Stoss wäre. Das ist ja exakt mein Problem was ich habe. |
Eben doch. Deshalb habe ich es dich ja machen lassen! Der Winkel zwischen der Geschwindigkeit der grünen und der roten Kugel NACH DEM STOSS beträgt doch 90°!
Ich habe es mit folgenden Einstellungen gemacht:
Grüne Kugel:
Geschwindigkeit: 2,5 m/s
Masse: 100 g
Stoßparameter: 2 mm
Winkel: 0°
Rote Kugel:
Geschwindigkeit: 0 m/s
Masse: 100 g
Ergebnis:
Die rote Kugel bewegt sich nach dem Stoß nahezu mit der Geschwindigkeit, die die grüne vorher hatte - nahezu waagrecht, aber wenig nach unten. Die grüne Kugel bewegt sich sehr langsam fast senkrecht nach oben, aber leicht nach rechts. Somit besteht zwischen den beiden letzteren Bewegungsrichtungen ein rechter Winkel!
Probier's mal!
|
|
 |
franz
Anmeldungsdatum: 04.04.2009
Beiträge: 11583
|
 franz Verfasst am: 09. Apr 2016 23:29 Titel: franz Verfasst am: 09. Apr 2016 23:29 Titel: |
 |
|
Ein einfaches Beispiel für den zentralen schiefen elastischen Stoß, wo sich nur die Normalkomponenten der Geschwindigkeit (bezüglich der Stoßgeraden) ändern,


Mit Blick auf die Zeichnung also 
|
|
 |
NeoJones
Anmeldungsdatum: 09.04.2016
Beiträge: 6
|
 NeoJones Verfasst am: 10. Apr 2016 22:41 Titel: NeoJones Verfasst am: 10. Apr 2016 22:41 Titel: |
 |
|
Okay, es leuchtet mir jetzt ein. Einen 90 Grad Winkel habe ich dann aber auch nur wenn m1 = m2 ist.
Nun habe ich aber unterschiedliche Massen und auf dieser Seite die Werte wie folgt eingestellt:
grüne kugel:
speed = 5
masse = 200
stoßparameter = 3,3
winkel = 0
rote kugel:
speed = 0
masse = 160
Laut Ergebnis auf der Seite hat die grüne Kugel den Winkel  von 154 Grad. von 154 Grad.
Benutze ich aber folgende Formeln, kommt bei mir ein ganz anderer Winkel raus:
 = \frac{b}{r_{1} + r_{2} })
 = \frac{m_{1}v_{1} - m_{2}u_{2} \cos(\beta ) }{m_{1}u_{1} } )
Für den Radius habe ich 10mm verwendet, da dort keine Angabe war.
 = 3,3 / 20 = 0,165 = 3,3 / 20 = 0,165
 = arcSin(0,165) = ~0,165749 (Radianten) = arcSin(0,165) = ~0,165749 (Radianten)
 = (180 / Pi) * ~0,165749 = 9,4967 Grad = (180 / Pi) * ~0,165749 = 9,4967 Grad
 = 200*5 - 160*0*cos(9,4967) = ~841,77 = 200*5 - 160*0*cos(9,4967) = ~841,77
 = ~841,77 / (200*5) = ~0,841 = ~841,77 / (200*5) = ~0,841
 = arcCos(0,841) = ~1,3757 (Radianten) = arcCos(0,841) = ~1,3757 (Radianten)
 = (180 / Pi) * ~1,3757 = 78,82 Grad = (180 / Pi) * ~1,3757 = 78,82 Grad
Also entweder stimmen die Ergebnisse auf der Seite nicht oder ich habe Fehler gemacht, kann mir da einer helfen?
|
|
 |
E=mc²
Anmeldungsdatum: 24.06.2014
Beiträge: 494
|
 E=mc² Verfasst am: 11. Apr 2016 22:12 Titel: E=mc² Verfasst am: 11. Apr 2016 22:12 Titel: |
 |
|
| NeoJones hat Folgendes geschrieben: | | Okay, es leuchtet mir jetzt ein. Einen 90 Grad Winkel habe ich dann aber auch nur wenn m1 = m2 ist. |
Ist dir auch klar, warum das so ist; also konntest du Herleitung dieser Tatsache in der Zwischenzeit nachvollziehen? Vorher hast du ja geschrieben, dass du es nicht verstehst.
Zum Rest:
Wie lautet jetzt genau die Aufgabe? Dann poste Sie bitte vollständig. Oder hast du eine erfunden -- wenn ja, dann poste auch diese vollständig.
| NeoJones hat Folgendes geschrieben: | | Für den Radius habe ich 10mm verwendet, da dort keine Angabe war. |
Du kannst nicht einfach irgendwelche Werte erfinden und dich dann wundern, dass die Ergebnisse nicht übereinstimmen.
|
|
 |
NeoJones
Anmeldungsdatum: 09.04.2016
Beiträge: 6
|
 NeoJones Verfasst am: 11. Apr 2016 23:17 Titel: NeoJones Verfasst am: 11. Apr 2016 23:17 Titel: |
 |
|
| Zitat: | | Ist dir auch klar, warum das so ist; also konntest du Herleitung dieser Tatsache in der Zwischenzeit nachvollziehen? Vorher hast du ja geschrieben, dass du es nicht verstehst. |
Nein, ich habe es jetzt einfach so hingenommen, das es einfach so ist. Ich habe in einem sehr gut umgesetzten Billardspiel gesehen, das es dort anders verlief, sodass kein rechter Winkel zustande kommt. Da ich mich aber nun mehr mit diesem Thema beschäftigt habe, ist mir klar geworden, das dort unterschiedliche Massen verwendet worden sind.
| Zitat: | | Wie lautet jetzt genau die Aufgabe? Dann poste Sie bitte vollständig. Oder hast du eine erfunden -- wenn ja, dann poste auch diese vollständig. |
Nein nein, es gibt keine Aufgabe oder Arbeit. Ich möchte ein 2d Billardspiel programmieren und bin auf der Suche nach Formeln, um a) die neuen Winkel der beiden Kugeln und b) die neue Geschwindigkeit auszurechnen.
Ich habe schon das halbe Internet durchsucht, aber es ist nicht so ganz einfach für jemanden, der es nicht gerade studiert.
Mich interessiert, wie und mit welcher Rechnung man bei der Simulation mit der grünen und roten Kugel auf diese Ergebnisse kommt...
Ich kann rechnen, wie ich will - ich komme nicht mal ansatzweise auf diese Ergebnisse und ich möchte verstehen, was an den Formeln, die ich gepostet habe, falsch ist. Wenn diese nicht falsch sind, muss ich ja irgendwo einen Fehler gemacht haben....   
|
|
 |
NeoJones
Anmeldungsdatum: 09.04.2016
Beiträge: 6
|
 NeoJones Verfasst am: 11. Apr 2016 23:43 Titel: NeoJones Verfasst am: 11. Apr 2016 23:43 Titel: |
 |
|
Also folgende Aufgabe:
1 Kugel mit der Masse 200g stösst auf eine ruhende Kugel mit der Masse 160g.
Gegeben:
Geschwindigkeit 1.Kugel V1 = 5 m/s
Masse 1.Kugel m1 = 200g
Masse 2.Kugel m2 = 160g
Stossparameter b = 3,3 mm
Radius r1 = 10mm
Radius r2 = 10mm
Gesucht:
Winkel Alpha = 
Dies ist die Formel, die ich in diesem Forum gefunden habe, aber nicht verstehe, was U1 und U2 bedeuten:
 = \frac{m_{1}v_{1} - m_{2}u_{2} \cos(\beta ) }{m_{1}u_{1} } )
Deswegen habe ich weiter oben ja meine komplette Rechnung gepostet, damit man nachvollziehen kann, wie ich auf das Ergebnis gekommen bin...
|
|
 |
franz
Anmeldungsdatum: 04.04.2009
Beiträge: 11583
|
 franz Verfasst am: 12. Apr 2016 00:25 Titel: franz Verfasst am: 12. Apr 2016 00:25 Titel: |
 |
|
|
Das ist eine trigonometrische Fleißaufgabe; alles komplett neu: Saubere Skizze, Eintragen der Geschwindigkeiten vor (v) und nach (u) dem Stoß, Winkel und die Formeln für die (geänderten) Normalkomponenten und (bleibenden) Parallelkomponenten bezüglich der Stoßnormalen. Die Formeln für die u_N würde ich nicht aus diesem Forum nehmen sondern mir unabhängig besorgen. (Es ist immer riskant, an bestehende threads anzudocken.)
|
|
 |
NeoJones
Anmeldungsdatum: 09.04.2016
Beiträge: 6
|
 NeoJones Verfasst am: 12. Apr 2016 00:43 Titel: NeoJones Verfasst am: 12. Apr 2016 00:43 Titel: |
 |
|
| Zitat: | | Die Formeln für die u_N würde ich nicht aus diesem Forum nehmen sondern mir unabhängig besorgen. |
Aha. Hilft mir jetzt auch sehr gut weiter -.- Naja es gibt sicher auch noch andere Foren, wo man vielleicht in der Lage ist, mir wirklich zu helfen. Die Aufgabe ist klar genug gestellt.
|
|
 |
E=mc²
Anmeldungsdatum: 24.06.2014
Beiträge: 494
|
 E=mc² Verfasst am: 12. Apr 2016 02:06 Titel: E=mc² Verfasst am: 12. Apr 2016 02:06 Titel: |
 |
|
Ich würde einmal so weit gehen und sagen, dass es nahezu unmöglich ist, sich hinzusetzen und solche Formeln wie du sie willst aus dem Hut zu zaubern. Nicht weil es sie nicht gibt, sondern weil sie doch recht kompliziert sind. Ich würde mich viel mehr Schritt für Schritt herantasten, also zB
1) zentraler Stoß, gleiche Massen, 2. Kugel ruhend
2) zentraler Stoß, gleiche Massen, 2. Kugel nicht ruhend
3) zentraler Stoß, unterscheidliche Massen
4) nicht zentraler Stoß, gleich Massen, 2. Kugel ruhend
5) nicht zentraler Stoß, verschiedene Massen, 2. Kugel ruhend
6) allgemeiner Fall
Wenn du alle diese Schritte hintereinander betrachtest und verstehst, ist die Sache viel erfolgversprechender. Ich - als ebenfalls nicht studierter - könnte auch nicht aus dem stehgreif eine Lösung für den allgemeinen Fall presentieren.
Das von die anfangs verlinkte Bsp ist im Westenlichen auf Stufe 4 der von mir oben genannten Reihenfolge. Daher würde ich mir an deiner Stelle überlegen, ob du die ersten 3 verstehst.
Weiters würde ich dir -da du auf den allgemeinen Fall heraus willst und den auch in einem Computerprogramm umsetzen willst - anraten, das ganze in Vektorenform zu machen. Dir kommt es gar nicht so sehr darauf an, ob ein Winkel so und so viel Grad hat, du wirst einen Geschwindigkeitsvektor benötigen, da die einzelnen Kugeln in deiner Simulation ja auch Ortsvektoren haben werden - oder irre ich mich da?
| franz hat Folgendes geschrieben: | | Die Formeln für die u_N würde ich nicht aus diesem Forum nehmen sondern mir unabhängig besorgen. |
Was willst du damit sagen?
| franz hat Folgendes geschrieben: | | (Es ist immer riskant, an bestehende threads anzudocken.) |
Das stimmt, weil es dadurch leicht unübersichtlich wird und va. von weniger Leuten durchgelesen, da sich viele nicht so weit unten im thread andocken wollen.
Nach einigem Geschwafel meinerseits noch zu was inhaltlichem, nämlich zu der Frage, warum im anfangs von dir verlinken Beispiel ein rechter Winkel vorliegt.
Es gilt die Energieerhaltung und E=1/2 m v^2:
(v geschw. vor dem Stoß; u danach)

Die ganze Gleichung kannst du zu vereinfachungszwecken mit 2m multiplizieren:

und außerdem ist v2=0, da diese Kugel anfangs ja ruht:

was offensichlichtlich dem Satz von Phytagoras sehr ähnlich ist:


Was für Seitenlängen in einem Dreieck gilt, gilt auch für Vektoren. Auch wenn diese keine Wege, sondern Geschwindigkeiten repräsentieren, weil mathematisch sind sie ja immer noch das selbe.
So wie im Dreieck a und b normal aufeinander stehen müssen, damit der Phytagoräische Lehrsatz gilt (und umgekehrt auch aus seinem gelten in einem Dreieck folgt, dass die beiden Seiten normal aufeinander stehen müssen - das ist hier sehr wichtig), gilt eben hier, dass die Geschwindigkeitsvektoren u1 und u2 normal aufeinader stehen müssen, damit der Phytagoräische Lehrsatz für sie erfüllt sein kann. Und dieser muss - wie wir durch umformung der Energieerhaltung gezeigt haben, in diesem Spezialfall erfüllt sein.
Verständlich? Denn im Falle un Billard ist ja nicht selten, dass 2 Kugeln der selben Masse aufeinander Stoß, wobei eine davon ruht, nämlich immer dann wenn die Kugel, die vorher von der weißen (die ja eine andere Masse hat) angestoßen wurde und auf eine nächste trifft. Somit ist dieser Fall für dich nicht ganz irrelevant.
Und jetzt noch etwas für den allgemeinen Fall:
Du hast am Ende 4 Unbekannte:
Die x- und y-Kompente von u1 und u2.
Du hast außerdem 3 Gleichungen:
1. Energieerhaltung
2. Impulserhaltung in x-Richtung
3. Impulserhaltung in y-Richtung
solange du weniger Gleichungen als Unbekannte hast, ist das Problem nicht lösbar.
Du kannst aber noch eine Sache sagen: Wenn sich die beiden Kugeln (bzw in 2D betrachtet Kreise) berühren, gibt es eine Gerade, die beide Kreise berüht, aber nicht scheindet. Jegliche Kraft und damit aus Impuls- und damit aus Geschwindigkeitsänderung erfolgt normal zu dieser Geraden.
So kommst du zu einer weiteren Bedingung, sodass es lösbar wird.
Man kann die Sache vlt auch vereinfachen, indem man sich aus dem Schwerpunktsystem betrachtet und für die Umsetzung ggf. davor und danach vom Billardtischsystem im Schwerpunktsystem der Stoßpartner wechselt oder indem man sie aus dem Schwerpunktsystem einer der Stoßpartner wechselt, sodass dieser für die Berechnung ruht (falls er sich nicht schon tut)
| Beschreibung: |
|

Download |
| Dateiname: |
stoss1.png |
| Dateigröße: |
22.81 KB |
| Heruntergeladen: |
566 mal |
|
|
 |
franz
Anmeldungsdatum: 04.04.2009
Beiträge: 11583
|
 franz Verfasst am: 12. Apr 2016 02:50 Titel: franz Verfasst am: 12. Apr 2016 02:50 Titel: |
 |
|
Der schiefe zentrale elastische Stoß ist ein gängiges Thema in der Literatur: Die Parallelkomponenten (senkrecht zur Stoßgeraden) bleiben, die Normalkomponenten ändern sich (Bezeichnungen unterschiedlich):
v_{1N}+2m_2v_{2N}}{m_1+m_2})
v_{2N}}{m_1+m_2})
Es bleibt noch: eine saubere Skizze und Bestimmung des gesuchten Winkels zwischen u_1 und u_2. (Oft ist auch der Streuwinkel zwischen v_1 und u_1 von Interesse.)
|
|
 |
|
|

















