| Autor |
Nachricht |
johnny87658
Anmeldungsdatum: 22.12.2014
Beiträge: 1
|
 johnny87658 Verfasst am: 22. Dez 2014 18:06 Titel: Widerstand eines Bügels johnny87658 Verfasst am: 22. Dez 2014 18:06 Titel: Widerstand eines Bügels |
 |
|
Meine Frage:
Ein elektrischer Leiter hat die Form eines Bügels mit rechteckförmigem Querschnitt. Die Radien betragen r1=60mm und r2=120mm. Der Bügel ist b=30mm breit. Das Leitermaterial hat den spezifischen Widerstand roh= 20[Ohm*m].
Welcher Widerstand R besteht zwischen den Leitenden Flächen A und B?
Meine Ideen:
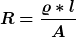
A = Flächeninhalt der Rechtecksfläche A und der Fläche B
l ist in dem Fall der Umfang des Bügels.

<br />
\Rightarrow R &=& \varrho *((90mm*\pi)/(30mm*60mm)))
[as_string: Ich hab versucht, Deine Formeln etwas leserlicher zu gestalten. Ich hoffe, es passt so]
|
|
 |
Pfirsichmensch
Anmeldungsdatum: 09.08.2014
Beiträge: 284
|
 Pfirsichmensch Verfasst am: 22. Dez 2014 18:29 Titel: Pfirsichmensch Verfasst am: 22. Dez 2014 18:29 Titel: |
 |
|
Wieso postest du zwei mal? So wird man dir auch nicht schneller helfen.
Und mach bitte mal eine Skizze ... ich will sicher gehen, dass es sich um den Bügel handelt an den ich grad denke.
Du nimmst die Bemessungsformel für Widerstände die eigentlich einen homogenen Stromfluss garantieren, machst aber den Radius nun unendlich klein und integrierst. Die Länge ist der halbe Kreisumfang also pi * r

Das Integral überlass ich nun dir!
|
|
 |
GvC
Anmeldungsdatum: 07.05.2009
Beiträge: 14861
|
 GvC Verfasst am: 26. Dez 2014 15:17 Titel: GvC Verfasst am: 26. Dez 2014 15:17 Titel: |
 |
|
| Pfirsichmensch hat Folgendes geschrieben: | | ... machst aber den Radius nun unendlich klein ... |
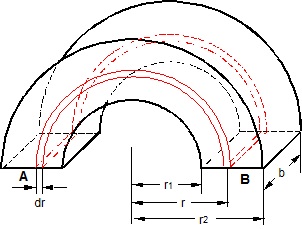
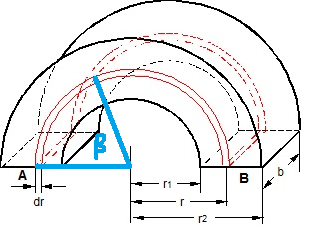
Das ist ein bisschen missverständlich. Nicht der Radius ist unendlich klein, sondern die Radiendifferenz des infinitesimal kleinen Volumenelementes, wie es in rot in nachfolgender Skizze eingezeichnet ist. Ich gehe mal davon aus, dass das der Bügel ist, den johnny87658 gemeint hat. Außerdem gehe ich genauso wie Du davon aus, dass mit den leitenden Flächen A und B die Schnittflächen des Halbzylinders gemeint sind. Das ist allerdings nicht sicher. Es könnte ja auch sein, dass damit die innere und die äußere Halbzylindermantelfläche gemeint sind, es sich also um eine radiale Strömung handelt. Leider hat sich johnny87658 darüber ausgeschwiegen.
Unter der Annahme, dass es sich um eine tangentiale Strömung zwischen den Schnittflächen des Halbzylinders handelt, ist es allerdings einigermaßen verwegen, den Widerstand des roten Elementes mit dR zu bezeichnen. Denn darunter versteht man im Allgemeinen einen infinitesimal kleinen Widerstand. Der Widerstand dieses infinitesimal kleinen Volumenelementes ist wegen seiner infinitesimal kleinen Querschnittsfläche jedoch unendlich groß.
Tatsächlich ist es sowieso sinnvoller, den Leitwert dieses Volumenelementes zu betrachten. Denn der gesamte Bügel besteht aus unendlich vielen parallelen Halbzylinderschalen mit der Wanddicke dr. Bei der Berechnung des Gesamtwiderstandes einer Parallelschaltung sind ja bekanntermaßen zunächst die Leitwerte zu addieren. Die Addition infinitesimal kleiner Elemente ist nun mal die Integration.
Außerdem würde ich in der Formel für den Widerstand bzw. für den Leitwert nicht die Leitfähigkeit 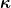 verwenden, wenn doch stattdessen laut Aufgabenstellung der spezifische Widerstand verwenden, wenn doch stattdessen laut Aufgabenstellung der spezifische Widerstand 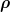 gegeben ist. Also besser gegeben ist. Also besser
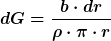
Das kann man nun von r1 bis r2 integrieren und davon dann den Kehrwert nehmen.
| Beschreibung: |
|
| Dateigröße: |
29.12 KB |
| Angeschaut: |
5453 mal |
|
|
|
 |
franz
Anmeldungsdatum: 04.04.2009
Beiträge: 11583
|
 franz Verfasst am: 26. Dez 2014 22:16 Titel: franz Verfasst am: 26. Dez 2014 22:16 Titel: |
 |
|
Eine Frage am Rande: Wie sieht eigentlich das elektrische Feld im Innern aus, oder anschaulich: Warum sollen die Elektronen den roten Weg nehmen, wenn's auch kürzer geht?

|
|
 |
GvC
Anmeldungsdatum: 07.05.2009
Beiträge: 14861
|
 GvC Verfasst am: 27. Dez 2014 17:03 Titel: GvC Verfasst am: 27. Dez 2014 17:03 Titel: |
 |
|
| franz hat Folgendes geschrieben: | | Warum sollen die Elektronen den roten Weg nehmen, wenn's auch kürzer geht? |
Was meinst Du mit "kürzer"? Kannst Du eventuelle kürzere Wege mal skizzieren?
|
|
 |
franz
Anmeldungsdatum: 04.04.2009
Beiträge: 11583
|
 franz Verfasst am: 28. Dez 2014 08:55 Titel: franz Verfasst am: 28. Dez 2014 08:55 Titel: |
 |
|
Guten Morgen GvC!
Kürzer würde der "rote" halbkreisförmige Weg, wenn man sich ihn als gespannten Gummifaden denkt, sich noch zusammenziehen kann. (Du schreibst ja selber "Unter der Annahme, dass es sich um eine tangentiale Strömung zwischen den Schnittflächen des Halbzylinders handelt" - und meine Frage richtet sich nur auf diese Annahme.)
mfG!
|
|
 |
GvC
Anmeldungsdatum: 07.05.2009
Beiträge: 14861
|
 GvC Verfasst am: 28. Dez 2014 12:40 Titel: GvC Verfasst am: 28. Dez 2014 12:40 Titel: |
 |
|
Hallo franz,
das hört sich ein bisschen so an wie die Vorstellung von Studienanfängern, die die Aussage "der Strom nimmt den Weg des geringsten Widerstandes" so interpretieren, dass der gesamte Strom durch den kleinsten Widerstand fließt. Der ganze Bügel setzt sich aus sehr vielen Halbzylinderschalen zusammen, die parallel geschaltet sind. Der Strom teilt sich entsprechend den Leitwerten dieser Halbzylinderschalen auf. Jedenfalls ist die Ladungsträgerbewegung an den Schnittflächen A und B, die ja Äquipotentialflächen darstellen, senkrecht zu diesen Flächen gerichtet. Es ist überhaupt nicht einzusehen, warum die Ladungsträger in einer Schale plötzlich nach innen ausweichen sollten. Denn dort fließen ja schon eintsprechend viele Ladungsträger mit den der Stromteilerregel entsprechenden Geschwindigkeiten.
Meine Aussage "unter der Annahme einer tangentialen Strömung" war als Alternative zu einer radialen Strömung gemeint, bei der die Spannung zwischen innerer und äußerer Mantelfläche des Halbzylinders anliegt. Aus der Aufgabenstellung ging nämlich nicht hervor, zwischen welchen Elektroden die Spannung angelegt wird. Das ist selbst jetzt noch nicht klar, denn der ursprüngliche Fragesteller hat sich seit seinem Eröffnungspost nicht wieder gemeldet.
Sollte es sich um eine radiale Strömung handeln, so ist der Gesamtwiderstand natürlich eine Reihenschaltung der "roten" Elemente zwischen r1 und r2 mit

|
|
 |
Derger
Anmeldungsdatum: 12.08.2017
Beiträge: 9
|
 Derger Verfasst am: 12. Aug 2017 20:22 Titel: Derger Verfasst am: 12. Aug 2017 20:22 Titel: |
 |
|
Hey,
ich bin bei meinen Fernstudium jetzt im zweiten Semester und habe die selber aufgabe gerade vor mir liegen.
Ich soll den Widerstand eine halbierten Holzylinders berechnen.
Der sieht also so aus wie auf dem Bild von GvC.
Der Strom fließt durch die Kontaktflächen A und B.
Also habe ich schon diese formel Aufgestellt.

dann r separiert.
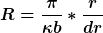
Und jetzt Integrieren.
Passt das bis hierher?
Leider habe ich keine Ahnung, und zu wenig Erfahrung wie ich jetzt r/dr intergrieren soll.
dr/r geht, das wäre ja ln(r) aber so herum....
Muß nicht die länge und die Fläche nach r intgriert werden da doch bei Variable sind?
Habe da noch verständnis Probleme.
Danke für eure Hilfe
PS: wenn es noch Fragen gibt ich Antworte euch ;-)
|
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18016
|
 TomS Verfasst am: 13. Aug 2017 01:18 Titel: TomS Verfasst am: 13. Aug 2017 01:18 Titel: |
 |
|
| GvC hat Folgendes geschrieben: | | Der ganze Bügel setzt sich aus sehr vielen Halbzylinderschalen zusammen, die parallel geschaltet sind. Der Strom teilt sich entsprechend den Leitwerten dieser Halbzylinderschalen auf. |
In welche infinitesimalen Elemente man den Bügel unterteilt ist zunächst mal willkürlich und darf physikalisch keine Rolle spielen. Es muss also geklärt werden, warum eine bestimmte Unterteilung sinnvoll ist und warum der Strom gerade dieser folgen sollte.
Ich halte die Frage von Franz für durchaus berechtigt.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
ML
Anmeldungsdatum: 17.04.2013
Beiträge: 3388
|
 ML Verfasst am: 13. Aug 2017 10:31 Titel: ML Verfasst am: 13. Aug 2017 10:31 Titel: |
 |
|
Hallo,
| Derger hat Folgendes geschrieben: |
ich bin bei meinen Fernstudium jetzt im zweiten Semester und habe die selber aufgabe gerade vor mir liegen.
Ich soll den Widerstand eine halbierten Holzylinders berechnen.
Der sieht also so aus wie auf dem Bild von GvC.
Der Strom fließt durch die Kontaktflächen A und B.
|
Du kennst die Gleichung 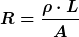 bzw. bzw. 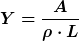 für einen Zylinder. für einen Zylinder.
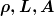 sind der spezifische Widerstand, die Länge und die Querschnittsfläche. sind der spezifische Widerstand, die Länge und die Querschnittsfläche.
Diese Gleichung wendest Du sinngemäß und (exemplarisch) auf den rot eingezeichneten Streifen (gebogener Zylinder) an:
Dessen Querschnittsfläche ist 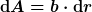 und die Länge ist und die Länge ist 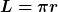 . .
Der Leitwert für einen beliebigen solchen roten Streifen (mit dem Radius r) ist somit:
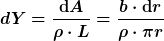
Für den Gesamtleitwert der parallel angeordneten Streifen ergibt sich:

Wenn Du das Integral berechnet hast, rechnest Du noch R=1/Y.
Kommst Du ab dem Punkt selbst weiter?
Viele Grüße
Michael
|
|
 |
ML
Anmeldungsdatum: 17.04.2013
Beiträge: 3388
|
 ML Verfasst am: 13. Aug 2017 11:08 Titel: ML Verfasst am: 13. Aug 2017 11:08 Titel: |
 |
|
| TomS hat Folgendes geschrieben: | | GvC hat Folgendes geschrieben: | | Der ganze Bügel setzt sich aus sehr vielen Halbzylinderschalen zusammen, die parallel geschaltet sind. Der Strom teilt sich entsprechend den Leitwerten dieser Halbzylinderschalen auf. |
In welche infinitesimalen Elemente man den Bügel unterteilt ist zunächst mal willkürlich und darf physikalisch keine Rolle spielen. Es muss also geklärt werden, warum eine bestimmte Unterteilung sinnvoll ist und warum der Strom gerade dieser folgen sollte.
Ich halte die Frage von Franz für durchaus berechtigt. |
Mathematisch sauber beantworten lässt sich die Frage m. E. nur durch Lösung der zugehörigen DGL.
Heuristisch bietet sich eine andere Erklärung an:
Es geht ja um die Frage, ob sich angesichts der Äquipotentialflächen an den jeweiligen Stirnseiten eine Radialkomponente des E-Feldes ausbilden kann.
Wenn wir uns einen einzelnen solchen "roten" Streifen anschauen und kurz annehmen, dass dieser elektrisch gegenüber den Nachbarstreifen isoliert ist, ergibt sich ein elektrische Potential  , das nur vom Winkel , das nur vom Winkel 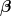 abhängt: abhängt:
 = \varphi_1 + \frac{\beta}{180^\circ} \cdot (\varphi_2-\varphi_1))
(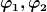 : elektrisches Potential an der linken/rechten Stirnfläche). : elektrisches Potential an der linken/rechten Stirnfläche).
Diese Potentialverteilung wächst/sinkt in 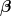 -Richtung so gleichmäßig, da wir einen von -Richtung so gleichmäßig, da wir einen von 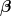 unabhängigen spezifischen Widerstand annehmen, und sie gilt aufgrund der Annahme von Aquipotentialflächen an den Stirnseiten unabhängig vom betrachteten Radius unabhängigen spezifischen Widerstand annehmen, und sie gilt aufgrund der Annahme von Aquipotentialflächen an den Stirnseiten unabhängig vom betrachteten Radius  des Streifens. des Streifens.
Wenn bei isolierten Streifen das Potential nur vom Winkel 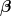 abhängt, dann wird sich beim gedanklichen Entfernen der Isolation daran nichts ändern, da es angesichts der Potentialverteilung keine stromtreibende Kraft in Radiusrichtung gibt. Der Strom fließt also weiterhin nur auf Strombahnen mit konstantem Radius. abhängt, dann wird sich beim gedanklichen Entfernen der Isolation daran nichts ändern, da es angesichts der Potentialverteilung keine stromtreibende Kraft in Radiusrichtung gibt. Der Strom fließt also weiterhin nur auf Strombahnen mit konstantem Radius.
Viele Grüße
Michael
| Beschreibung: |
|
| Dateigröße: |
42.74 KB |
| Angeschaut: |
3634 mal |
|
|
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18016
|
 TomS Verfasst am: 13. Aug 2017 11:55 Titel: TomS Verfasst am: 13. Aug 2017 11:55 Titel: |
 |
|
| ML hat Folgendes geschrieben: | | Mathematisch sauber beantworten lässt sich die Frage m. E. nur durch Lösung der zugehörigen DGL. |
Ja; siehe jedoch unten (*)
| ML hat Folgendes geschrieben: | Wenn bei isolierten Streifen das Potential nur vom Winkel 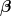 abhängt, dann wird sich beim gedanklichen Entfernen der Isolation daran nichts ändern, da es angesichts der Potentialverteilung keine stromtreibende Kraft in Radiusrichtung gibt. Der Strom fließt also weiterhin nur auf Strombahnen mit konstantem Radius. abhängt, dann wird sich beim gedanklichen Entfernen der Isolation daran nichts ändern, da es angesichts der Potentialverteilung keine stromtreibende Kraft in Radiusrichtung gibt. Der Strom fließt also weiterhin nur auf Strombahnen mit konstantem Radius. |
Ja, nach dieser Argumentation.
Andererseits wäre der Widerstand entlang kürzerer Kurven kleiner. Ich bin noch nicht überzeugt, dass die Entfernung der Isolation ein erlaubter Kunstgriff ist. Z.B. weiß man aus der Plasmaphysik, dass die Stromdichte am Innenrand eines torusförmigen Plasmas ansteigt.
Ich denke aber, man sollte auch einfacher als mit der Lösung der DGL argumentieren können (*) Evtl. kann man mit einem exakt zylindersymmetrischen Leiter mit kreisförmigem Querschnitt und dessen Randbedingungen und Stromdichte beginnen und zeigen, dass eine Deformation der Form des Leiters nicht (bzw. in einer gewissen Näherung nicht maßgeblich) zu einer Deformation der Stromdichte durch den weiterhin kreisförmigem Querschnitt führt.
|
|
 |
ML
Anmeldungsdatum: 17.04.2013
Beiträge: 3388
|
 ML Verfasst am: 13. Aug 2017 12:54 Titel: ML Verfasst am: 13. Aug 2017 12:54 Titel: |
 |
|
Hallo,
| Zitat: |
Andererseits wäre der Widerstand entlang kürzerer Kurven kleiner. Ich bin noch nicht überzeugt, dass die Entfernung der Isolation ein erlaubter Kunstgriff ist. Z.B. weiß man aus der Plasmaphysik, dass die Stromdichte am Innenrand eines torusförmigen Plasmas ansteigt. |
Mit meiner Argumentation haben wir am Innenrand des Bügels die elektrische Feldstärke 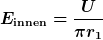 und am Außenrand entsprechend und am Außenrand entsprechend 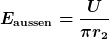 . .
(Mit 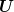 meine ich die Potentialdifferenz meine ich die Potentialdifferenz 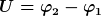 zwischen beiden Stirnflächen.) zwischen beiden Stirnflächen.)
Für die Stromdichte 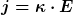 ( (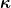 : spezifische Leitfähigkeit) folgt daraus: : spezifische Leitfähigkeit) folgt daraus:
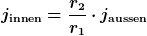
Wegen 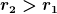 wäre das qualitativ gesehen ja genau das, was Du erwartest. wäre das qualitativ gesehen ja genau das, was Du erwartest.
(Ob das jetzt genau die gleichen Zusammenhänge wie bei einem Plasma sind, weiß ich nicht. Dazu kenne ich mich mit Plasmaphysik nicht genug aus. Vom Bauchgefühl her würde ich denken, dass ein Plasma sich deutlich komplizierter verhält. Wikipedia erwähnt im Zusammenhang mit Plasmaphysik sowohl die Maxwellgleichungen als auch die Navier-Stokes-Gleichung. Das hört sich nicht nach mathematisch leicht verdaulicher Kost an.)
| Zitat: |
Ich denke aber, man sollte auch einfacher als mit der Lösung der DGL argumentieren können (*) Evtl. kann man mit einem exakt zylindersymmetrischen Leiter mit kreisförmigem Querschnitt und dessen Randbedingungen und Stromdichte beginnen und zeigen, dass eine Deformation der Form des Leiters nicht (bzw. in einer gewissen Näherung nicht maßgeblich) zu einer Deformation der Stromdichte durch den weiterhin kreisförmigem Querschnitt führt. |
Ich hatte meinen Post ursprünglich genauso angefangen wollen und habe was von einem Kreisbogen mit 359° geschrieben. Ganz zumachen darf man den Kreisbogen gedanklich ja nicht, da man ansonsten keine Potentialdifferenz zwischen den beiden (nun elektrisch verbundenen) Stirnflächen annehmen kann und damit keine stromtreibende Kraft auftritt.
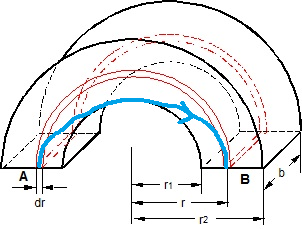
Wenn ich Dich richtig verstehe, würdest Du Dich gerne davon überzeugen, dass eine abgekürzte Strombahn, also beispielsweise sowas wie unten etwas wacklig in blau skizziert, nicht vorkommen kann.
Viele Grüße
Michael
| Beschreibung: |
|
| Dateigröße: |
41.71 KB |
| Angeschaut: |
3594 mal |
|
|
|
 |
Derger
Anmeldungsdatum: 12.08.2017
Beiträge: 9
|
 Derger Verfasst am: 13. Aug 2017 14:40 Titel: Derger Verfasst am: 13. Aug 2017 14:40 Titel: |
 |
|
| ML hat Folgendes geschrieben: |
Diese Gleichung wendest Du sinngemäß und (exemplarisch) auf den rot eingezeichneten Streifen (gebogener Zylinder) an:
Dessen Querschnittsfläche ist 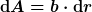 und die Länge ist und die Länge ist 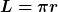 . .
Der Leitwert für einen beliebigen solchen roten Streifen (mit dem Radius r) ist somit:
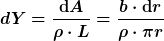
Für den Gesamtleitwert der parallel angeordneten Streifen ergibt sich:

Wenn Du das Integral berechnet hast, rechnest Du noch R=1/Y.
Kommst Du ab dem Punkt selbst weiter? |
Hey,
danke für die Hilfe.
die Richitge formel habe ich schon aufgestellt.
Ich habe nur 2 Probleme.
1:Warum berechne ich den Widerstand nur für einen dünnen streifen wenn der Widerstand des Gesamten Bogens gefragt ist.
2:Es ist ja eigentlich egal ob Leitwert oder Widerstand. Die Umrechnung ist ja einfach. Rechnet ihr nur deshalb mit dem Leitwert da hier die Integration einfacher ist? )
Würde die integration von 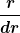 überhaupt funktionieren? überhaupt funktionieren?
Ich sehe hier sind Profis am Werk bei den anderen Kommentaren komm ich nicht ganz hinterher 
Viele Grüße
|
|
 |
ML
Anmeldungsdatum: 17.04.2013
Beiträge: 3388
|
 ML Verfasst am: 13. Aug 2017 15:59 Titel: ML Verfasst am: 13. Aug 2017 15:59 Titel: |
 |
|
Hallo,
| Derger hat Folgendes geschrieben: |
die Richitge formel habe ich schon aufgestellt.
|
Naja, meines Erachtens bist Du auf der Hälfte stehengeblieben.
| Zitat: |
1:Warum berechne ich den Widerstand nur für einen dünnen streifen wenn der Widerstand des Gesamten Bogens gefragt ist.
|
Es geht um den LEITWERT, nicht den Widerstand. Das ist nicht egal.
Du berechnest zunächst den Leitwert eines dünnen Streifens mit der Dicke  , weil das ein Zwischenschritt zur Lösung ist. Die einzelnen dünnen Streifen sind parallel geschaltet. In der Parallelschaltung addieren sich deren Leitwerte. , weil das ein Zwischenschritt zur Lösung ist. Die einzelnen dünnen Streifen sind parallel geschaltet. In der Parallelschaltung addieren sich deren Leitwerte.
Da die Streifen im gedanklichen Modell unendlich dünn sind, nutzt Du zu deren Addition eine Integration. Das Integral ist ja (ins Unreine gesprochen) sowas wie der Grenzwert der Summe über unendlich viele unendlich kleine Dinge.
| Zitat: |
2:Es ist ja eigentlich egal ob Leitwert oder Widerstand. Die Umrechnung ist ja einfach. Rechnet ihr nur deshalb mit dem Leitwert da hier die Integration einfacher ist? )
|
Die Umrechnung von Leitwert nach Widerstand ist einfach. Aber die weiteren Rechnungen sind nur mit Leitwerten einfach.
| Zitat: |
Würde die integration von 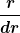 überhaupt funktionieren? überhaupt funktionieren?
|
Ich weiß gar nicht, ob so ein Ausdruck überhaupt definiert ist.
| Zitat: |
Ich sehe hier sind Profis am Werk bei den anderen Kommentaren komm ich nicht ganz hinterher 
|
Es geht dort um eine genauere Begründung der Rechenmethode und um die Frage, ob die Stromlinien entlang eines konstanten Radius verlaufen.
Viele Grüße
Michael
|
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18016
|
 TomS Verfasst am: 13. Aug 2017 22:11 Titel: TomS Verfasst am: 13. Aug 2017 22:11 Titel: |
 |
|
Für einen perfekt symmetrischen Fall kann man sicher so argumentieren wie ML:
Man startet mit einem symmetrischen Kreiszylinder der Länge L und Radius R, den man zu einem Torus mit Länge L der Mittelachse zusammenbiegt. An einer Stelle sei der Torus aufgeschnitten und bilde einen ideal isolierenden, unendlich dünnen Kondensator, so dass entlang L die Spannung U abfalle; alternativ darf man sich das auch als induzierte Ringspannung vorstellen. Die beiden Kreisflächen liegen dabei jeweils auf Potential Null bzw. U. Entlang einer beliebigen geschlossen Kurve (Windungszahl Eins) im Inneren des Torus liegt also eine Spannung U an.
Aufgrund der Symmetrie der Anordnung ist es ausreichend, toroidale Kreise zu betrachten, die parallel zur Achse des Torus um diesen umlaufen. Der elektrische Feldstärkevektor sowie der Stromdichtevektor wird in jedem Punkt parallel zu einer derartigen Kreislinie laufen; außerdem ist der Betrag der Stromdichte entlang einer derartigen Kreislinie konstant. Damit tritt der Stromdichtevektor senkrecht durch jeden Punkt jeder gedachten kreisförmigen Querschnittsfläche des Torus.
Für den Betrag des elektrischen Feldes entlang einer toroidalen Kreislinie mit Länge l gilt
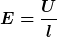
und für den Betrag der Stromdichte folgt
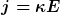
Führt man auf einer kreisförmigen Querschnittsfläche Polarkoordinaten rho und theta ein, so ist die Länge der Kurve l und damit die Stromdichte j eine Funktion dieser Polarkoordinaten.
Man beachte, dass in diese Argumentation die Symmetrie des Problems eingeht. Es ist also weiterhin nicht davon auszugehen, dass dies auch für nicht-symmetrische Anordnungen gilt.
Ein Gegenargument lautet wie folgt: nehmen wir den o.g. Fall des Torus, halbieren diesen und gehen weiterhin von einer unveränderten Stromdichte durch die kreisförmige Querschnittsfläche aus; kleben wir nun einen zweiten, jedoch geraden zylindrischen Leiter an diese Querschnittsfläche. Bei letzterem wäre die Stromdichte auf der Querschnittsfläche trivialerweise konstant, bei ersterem ist sie das gem. der o.g. Diskussion nicht. Damit führt die Argumentation auf eine unstetige Stromdichte an der Nahstelle zwischen beiden Leitern, was offensichtlich falsch ist. Verlängern von Leitern, Verbiegen usw. deformiert demnach die Stromdichte, d.h. ändert nicht nur den Betrag, sondern i.A. auch die Richtung der Stromdichte.
Ich berechne nochmal die Stromdichte nach MLs Methode auf der kreisförmigen Querschnittsfläche mit Radius R und Polarkoordinaten rho und theta; rho bezeichnet den Abstand eines Punktes vom Zentrum der Kreisfläche.
Für die Länge l einer toroidalen Kreislinie durch diesen Punkt gilt
 = L + 2\pi\,\rho\,\cos\theta)
Damit wäre
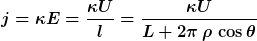
Nun sei
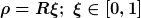
und damit
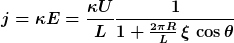
Damit erkennt man, dass die Deformation im Wesentlichen vom Längenverhältnis
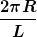
abhängt. Ist dieser Parameter klein, ist also der Radius einer Drahtschleife groß ggü. dem Radius des Drahtes selbst, darf man von einer über den Drahtquerschnitt konstanten Stromdichte ausgehen.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
ML
Anmeldungsdatum: 17.04.2013
Beiträge: 3388
|
 ML Verfasst am: 14. Aug 2017 02:55 Titel: ML Verfasst am: 14. Aug 2017 02:55 Titel: |
 |
|
Hallo TomS,
| Zitat: |
Man startet mit einem symmetrischen Kreiszylinder der Länge L und Radius R, den man zu einem Torus mit Länge L der Mittelachse zusammenbiegt.
|
Änderst Du die Aufgabenstellung ab, damit es noch symmetrischer wird?
| TomS hat Folgendes geschrieben: |
Man beachte, dass in diese Argumentation die Symmetrie des Problems eingeht. Es ist also weiterhin nicht davon auszugehen, dass dies auch für nicht-symmetrische Anordnungen gilt.
|
Ich bin noch nicht überzeugt, dass es allein um die Symmetrie geht.
Ich denke, dass ein ganz entscheidender Punkt die Annahme von Äquipotentialflächen an den Stirnseiten ist. Wenn diese Bedingung erfüllt ist, kann man m.E. den halben Torus weglassen, ohne dass das etwas an der Stromdichteverteilung ändert. Es ist aber nicht immer ohne weiteres möglich, diese Bedingung zu erfüllen.
| Zitat: |
Ein Gegenargument lautet wie folgt: nehmen wir den o.g. Fall des Torus, halbieren diesen und gehen weiterhin von einer unveränderten Stromdichte durch die kreisförmige Querschnittsfläche aus; kleben wir nun einen zweiten, jedoch geraden zylindrischen Leiter an diese Querschnittsfläche. Bei letzterem wäre die Stromdichte auf der Querschnittsfläche trivialerweise konstant, bei ersterem ist sie das gem. der o.g. Diskussion nicht. Damit führt die Argumentation auf eine unstetige Stromdichte an der Nahstelle zwischen beiden Leitern, was offensichtlich falsch ist.
|
Die Frage ist gut, aber wir müssen uns noch darüber unterhalten, was aus dem Sprung in der Stromdichtefunktion folgt.
Letztlich geht es doch um folgende Aussagen:
a) Die beiden Stirnflächen des geraden Zylinders sind jeweils Äquipotentialflächen.
b) Es existiert eine (örtlich) konstante Stromdichte über der Querschnittsfläche des geraden Zylinders.
c) Die beiden Stirnflächen des Torus sind jeweils Äquipotentialflächen.
d) Es existiert eine (örtlich) veränderliche Stromdichte über der Querschnittsfläche des Torus.
Meine Aussage lautet:
(ML1): Aus a) folgt b)
(ML2): Aus c) folgt d).
Dein Gegenargument lautet, wenn ich Dich richtig verstehe:
Wenn man den Torus und den geraden Zylinder leitend miteinander verbindet und weiterhin a) und c) voraussetzt, dann müssten entsprechend (ML1) und (ML2) gleichzeitig b) und d) gelten. Die daraus resultierende Unstetigkeit der Stromdichteverteilung an der Kontaktfläche beobachtet man in der Natur aber nicht. Also stimmen die Aussagen (ML1) und (ML2) nicht.
Meines Erachtens lautet die korrekte Folgerung aus Deinem Argument so: "Fügt man den Torus und den geraden Zylinder zusammen, lassen sich die Voraussetzungen a) und c) nicht beide zusammen einhalten. Die Kontaktfläche von Torus und Zylinder kann bei endlicher Leitfähigkeit des Materials keine Äquipotentialfläche bilden, da Ausgleichsströme innerhalb der Kontaktfläche (parallel zu dieser) fließen und mit diesen Strömen ein radiales E-Feld einhergeht".
Der entscheidende Punkt dafür, wie genau sich die von mir berechnete Feldverteilung einstellt, ist also, wie gut es gelingt, die Stirnflächen des Bügels zu Äquipotentialflächen zu machen. Ist der Bügel nur mäßig leitfähig, kann eine Beschichtung der Stirnflächen mit einem sehr gut leitfähigen Metall nützlich sein. Ideal wäre natürlich eine ideal leitfähige Kontaktfläche. Dann könnten beliebig große "Radialströme" innerhalb dieser Fläche fließen, ohne dass sich ein radiales E-Feld ausbildet. In diesem Grenzfall wären also auch Sprünge in der Stromdichteverteilung denkbar.
Viele Grüße
Michael
|
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18016
|
 TomS Verfasst am: 14. Aug 2017 07:38 Titel: TomS Verfasst am: 14. Aug 2017 07:38 Titel: |
 |
|
| ML hat Folgendes geschrieben: | Hallo TomS,
| Zitat: |
Man startet mit einem symmetrischen Kreiszylinder der Länge L und Radius R, den man zu einem Torus mit Länge L der Mittelachse zusammenbiegt.
|
Änderst Du die Aufgabenstellung ab, damit es noch symmetrischer wird?
| TomS hat Folgendes geschrieben: |
Man beachte, dass in diese Argumentation die Symmetrie des Problems eingeht. Es ist also weiterhin nicht davon auszugehen, dass dies auch für nicht-symmetrische Anordnungen gilt.
|
Ich bin noch nicht überzeugt, dass es allein um die Symmetrie geht.
Ich denke, dass ein ganz entscheidender Punkt die Annahme von Äquipotentialflächen an den Stirnseiten ist. |
Ich ändere die Aufgabenstellung zunächst ab, um sicher zu gehen, dass die Symmetrie tatsächlich vorliegt. Diese gilt dann für j und E.
Die Symmetrie gilt sicher für den Kreis-Torus sowie für den Kreis-Zylinder. Dann zeige ich, dass ein Halbieren des Torus ohne Berücksichtigung der Brechung dessen Symmetrie zu zwei inkompatiblen Lösungen führt. Also muss die Brechung der Symmetrie des Torus auch die Symmetrie von j und E brechen, und zwar indem eine Deformation der Form der Vektorfelder erfolgt.
Die Äquipotentialflächen an den gedachten Stirnflächen gelten für die noch ungebrochene Symmetrie des Torus. Beim Aufschneiden bzw. Halbieren desselben kann ich die Existenz der Äquipotentialflächen sicherstellen, indem ich beide auf gleiches Potential zwinge, nämlich z.B. durch Annahme einer perfekt leitenden Schicht auf diesen Grenzflächen. Es ist aber klar, dass wenn diese Annahme ebenfalls noch wegfallen soll, dass dann das Problem noch vertrackter wird.
| ML hat Folgendes geschrieben: | | Wenn diese Bedingung erfüllt ist, kann man m.E. den halben Torus weglassen, ohne dass das etwas an der Stromdichteverteilung ändert. Es ist aber nicht immer ohne weiteres möglich, diese Bedingung zu erfüllen. |
Aber mein Argument zeigt doch, dass selbst unter Beibehaltung dieser Bedingung das Weglassen des halben Torus zu einer mit den geraden Kreiszylinder inkompatiblen Lösung führt. Die Schlussfolgerung daraus ist, dass das Halbieren des Torus sowie das Zusammenkleben mit dem Zylinder die Feldkonfiguration in beiden ändern muss.
| ML hat Folgendes geschrieben: | | Die Frage ist gut, aber wir müssen uns noch darüber unterhalten, was aus dem Sprung in der Stromdichtefunktion folgt. |
Der Sprung ist unzulässig.
| ML hat Folgendes geschrieben: | Letztlich geht es doch um folgende Aussagen:
a) Die beiden Stirnflächen des geraden Zylinders sind jeweils Äquipotentialflächen.
b) Es existiert eine (örtlich) konstante Stromdichte über der Querschnittsfläche des geraden Zylinders.
c) Die beiden Stirnflächen des Torus sind jeweils Äquipotentialflächen.
d) Es existiert eine (örtlich) veränderliche Stromdichte über der Querschnittsfläche des Torus. |
Ja (ich gehe davon aus, dass du bei c - d) noch von den gedachten Stirnflächen innerhalb des vollständigigen Zylinders sprichst).
| ML hat Folgendes geschrieben: | Meine Aussage lautet:
(ML1): Aus a) folgt b)
(ML2): Aus c) folgt d). |
Dem stimme ich für den noch symmetrischen Fall des einzelnen Zylinders sowie des ganzen Torus zu.
| ML hat Folgendes geschrieben: | Dein Gegenargument lautet, wenn ich Dich richtig verstehe:
Wenn man den [halbierten]Torus und den geraden Zylinder leitend miteinander verbindet und weiterhin a) und c) voraussetzt, dann müssten entsprechend (ML1) und (ML2) gleichzeitig b) und d) gelten. Die daraus resultierende Unstetigkeit der Stromdichteverteilung an der Kontaktfläche beobachtet man in der Natur aber nicht. Also stimmen die Aussagen (ML1) und (ML2) nicht. |
Da bin ich mir nicht sicher.
Man kann m.E. weder die Symmetrie der Stromdichten noch die Forderung der Äquipotentialfläche für die Kontaktfläche aufrechterhalten. Ich will ja auch nur zeigen, dass dies für den halbierten Torus nicht geht, mehr nicht.
| ML hat Folgendes geschrieben: | | Meines Erachtens lautet die korrekte Folgerung aus Deinem Argument so: "Fügt man den Torus und den geraden Zylinder zusammen, lassen sich die Voraussetzungen a) und c) nicht beide zusammen einhalten. Die Kontaktfläche von Torus und Zylinder kann bei endlicher Leitfähigkeit des Materials keine Äquipotentialfläche bilden, da Ausgleichsströme innerhalb der Kontaktfläche (parallel zu dieser) fließen und mit diesen Strömen ein radiales E-Feld einhergeht". |
Mein Argument ist rein topologisch.
Nach dem idealen Verkleben liegt in der Kontaktstelle keine lokale Besonderheit vor, und damit kann die Feldgeometrie auch nicht durch irgendeine lokale Betrachtung gerettet werden. Das Verkleben hat globale Auswirkung auf die Feldgeometrie in die beiden Körper hinein.
| ML hat Folgendes geschrieben: | | In diesem Grenzfall wären also auch Sprünge in der Stromdichteverteilung denkbar. |
Wie gesagt, ich gehe von einer idealen Verklebung aus, d.h. die Kontaktfläche weißt keine lokalen Besonderheiten auf.
Das Argument zeigt nur, dass das elektrische Feld sowie das Feld für die Stromdichte glatt aneinander gefügt werden müssen, und dass deswegen die in den beiden einzelnen Körpern vorliegenden Feldern geändert werden müssen; damit liegt möglicherweise auch keine Äquipotentialfläche mehr vor.
Zusammenfassend: das Verkleben der gesicherten Feldkonfiguration des Zylinders sowie das der angenommenen Feldkonfiguration des halbierten Torus - die aus dem vollständigen Torus abgeleitet wurde - zeigt eine Inkonsistenz und erfordert eine Deformation der Feldkonfigurationen. Wenn dies so ist, dann ist völlig unklar, wieso erst das Verkleben von Zylinder und halbierten Torus zu dieser Problematik führt und nicht bereits das Halbieren des Torus selbst. Ich behaupte, mein Argument zeigt (motiviert), dass bereits das Halbieren des Torus dessen Symmetrie und damit die der Felder bricht.
Diesen Punkt sollten wir uns vornehmen: existiert ein Argument, das gesichert beweist, dass das Halbieren die Felder nicht ändert?
|
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18016
|
 TomS Verfasst am: 14. Aug 2017 07:58 Titel: TomS Verfasst am: 14. Aug 2017 07:58 Titel: |
 |
|
@Derger: Anbei eine kurze Skizze zur Berechnung.
Nimm' an, auf einer Querschnittsfläche = Äquipotentialfläche S mit den o.g. Koordinaten sei das senkrecht hindurchtretende elektrische Feld sowie die ebenfalls senkrecht hindurchtretende Stromdichte bekannt.
Lokal gilt
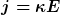
Die Stromstärke durch beide Äquipotentialflächen lautet
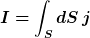
wobei dS und j hier Skalare sind, da j senkrecht durch S hindurchtritt.
Außerdem gilt
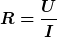

Nach der weiter oben stehenden Argumentation ist
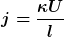
Einsetzen liefert

wobei l die Länge des Strompfades bezeichnet (es muss über alle Strompfade d.h. über die gesamte Querschnittsfläche = Äquipotentialfläche integriert werden; die Formel gilt dann allgemein)
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18016
|
 TomS Verfasst am: 14. Aug 2017 11:31 Titel: TomS Verfasst am: 14. Aug 2017 11:31 Titel: |
 |
|
Sorry, ich hoffe die vielen Posts stören nicht.
Nochmal zu meiner Argumentation bzgl. des Verklebens von halbem Torus und Zylinder: diese Argumentation ist bzgl. des halbierten Torus alleine wertlos; Ursache dafür ist die Kombination inkompatibler Symmetrien. Es ist jedoch möglich, mittels der Symmetrie des Torus alleine zu argumentieren und zu zeigen, dass diese ausreicht, um die Stromdichte zu bestimmen.
Dazu betrachtet man den vollständigen Torus mit maximal symmetrischer Stromdichte. Offensichtlich ist jede kreisförmige Querschnittsfläche eine Äquipotentialfläche. Damit ist es egal, ob diese Fläche als gedachte Querschnittsfläche im Inneren des intakten Torus liegt, oder ob man den Torus tatsächlich aufschneidet und das Potential auf dieser Schnittfläche fixiert; Potential und Feld und somit Stromdichte innerhalb des diesen Flächen berandeten Torus-Restes sind identisch.
Damit ist gezeigt, dass sich die Feldverteilung innerhalb eines beliebigen durch kreisförmige Querschnittsflächen berandete Torus-Restes aus der Feldverteilung des vollständigen Torus – eingeschränkt auf den Torus-Rest – resultiert.
|
|
 |
ML
Anmeldungsdatum: 17.04.2013
Beiträge: 3388
|
 ML Verfasst am: 14. Aug 2017 13:09 Titel: ML Verfasst am: 14. Aug 2017 13:09 Titel: |
 |
|
Hallo Tom,
| TomS hat Folgendes geschrieben: |
| ML hat Folgendes geschrieben: | | Meines Erachtens lautet die korrekte Folgerung aus Deinem Argument so: "Fügt man den Torus und den geraden Zylinder zusammen, lassen sich die Voraussetzungen a) und c) nicht beide zusammen einhalten. Die Kontaktfläche von Torus und Zylinder kann bei endlicher Leitfähigkeit des Materials keine Äquipotentialfläche bilden, da Ausgleichsströme innerhalb der Kontaktfläche (parallel zu dieser) fließen und mit diesen Strömen ein radiales E-Feld einhergeht". |
Mein Argument ist rein topologisch.
Nach dem idealen Verkleben liegt in der Kontaktstelle keine lokale Besonderheit vor, und damit kann die Feldgeometrie auch nicht durch irgendeine lokale Betrachtung gerettet werden. Das Verkleben hat globale Auswirkung auf die Feldgeometrie in die beiden Körper hinein.
|
Dem stimme ich zu.
| Zitat: | | Ich behaupte, mein Argument zeigt (motiviert), dass bereits das Halbieren des Torus dessen Symmetrie und damit die der Felder bricht. |
Das Halbieren bricht die Symmetrie des Torus, aber m. E. nicht unbedingt die der Felder. Ich gehe weiter unten drauf ein.
| Zitat: |
Diesen Punkt sollten wir uns vornehmen: existiert ein Argument, das gesichert beweist, dass das Halbieren die Felder nicht ändert? |
Ja, das ist die Frage.
Ich denke, wir sehen das Problem etwas klarer, wenn wir uns vergegenwärtigen, dass ein klassisches Randwertproblem vorliegt.
Welche Modellannahmen haben wir für den Rand des Körpers getroffen?
- Im vollsymmetrischen Fall mit einem komplett geschlossenen Torus* haben wir für den Rand des Torus die Bedingung 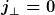 getroffen: Die Ladung bleibt im Körper drin. getroffen: Die Ladung bleibt im Körper drin.
- Wenn wir den Torus aufschneiden und zu einem Halbtorus machen, haben wir mit den Stirnflächen zwei zusätzliche Randflächen, über die wir Aussagen treffen müssen.
Wir haben die Wahl, ob wir dort das elektrische Potential oder eine Stromdichteverteilung vorgeben wollen. Beides beliebig vorzugeben geht normalerweise nicht, da sich dann Widersprüche* ergeben.
Wir müssen ohnehin aufpassen, dass wir physikalisch sinnvolle Randwerte vorgeben. So müssen beispielsweise der in das Volumen hineinfließende Strom bei unserer stationären Betrachtung gleich groß wie der hinausfließende Strom sein. Und die Stromdichteverteilung sollte am Rand natürlich stetig sein. (Ein Grenzfall wäre der schon erwähnte Kunstgriff der ideal leitfähigen Fläche, der die Stetigkeitsforderung abmildert).
Legen wir die Randbedingungen nur "irgendwie" fest, so wird sich im Halbtorus auch nur "irgend eine" Stromdichteverteilung ergeben.
Wenn wir die Randbedingungen an den beiden Stirnflächen des Halbtorus jedoch genau so festlegen, wie sie beim Volltorus im symmetrischen Fall wären, dann ergibt sich innerhalb des Halbtorus logischerweise die Stromdichteverteilung, die sich auch beim Volltorus ergeben würde.
Das heißt konkret: Wenn wir jeweils eine Äquipotentialfläche an den Stirnflächen erzwingen, haben wir tatsächlich im Halbtorus die gleiche Stromdichteverteilung wie im Volltorus. Wir müssen allerdings schauen, ob wir die Randbedingung tatsächlich herzustellen in der Lage sind, ohne gleich einen Volltorus zu bauen. Annähern können wir uns daran m. E. mit gut leitfähigen Stirnflächen.
- Vergrößern wir den Halbtorus dadurch, dass wir an dessen Stirnflächen einen passenden Zylinder ankleben, dann passiert folgendes:
a) Wir müssen uns nun aber Gedanken über die Randbedingungen an den Stirnflächen des geraden Zylinders machen.
b) Die Stromdichteverteilung an der Kontaktflächen von Halbtorus und den beiden Zylindern ist irgendeine Übergangsverteilung zwischen der des vollsymmetrischen Torus und der des unendlich langen Zylinders. Sie hängt bei einem kurzen Zylinder lokal von a) ab, bei langen Zylindern nur noch im Hinblick auf den Gesamtstrom. Die Kontaktfläche ist i. A. keine Äquipotentialfläche.
- Vergrößern wir den Halbtorus dadurch, dass wir an dessen Stirnflächen einen (dünnen) Draht befestigen, der einen vorgegebenen Strom führt, dann ergibt sich ebenfalls eine komplizierte Stromdichteverteilung.
Viele Grüße
Michael
* Das ist (ähnlich wie die Annahme mit der ideal leitfähigen Schicht) eine Modellannahme, die physikalisch nur näherungsweise eintritt. Wir können zwar über Induktion im vollsymmetrischen Fall einen Stromantrieb realisieren, aber das wird sicher kein Gleichstrom sein, da wir ja irgendwann einschalten müssen und die Flussdichte nicht unendlich lang hochschrauben können. Also müssen wir hier zeitliche Einschwingvorgänge berücksichtigen. Wir können uns aber natürlich schon vorstellen, wie die Vorgänge im Grenzfall langen Wartens wären.
|
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18016
|
 TomS Verfasst am: 14. Aug 2017 13:57 Titel: TomS Verfasst am: 14. Aug 2017 13:57 Titel: |
 |
|
| ML hat Folgendes geschrieben: | | Wenn wir die Randbedingungen an den beiden Stirnflächen des Halbtorus jedoch genau so festlegen, wie sie beim Volltorus im symmetrischen Fall wären, dann ergibt sich innerhalb des Halbtorus logischerweise die Stromdichteverteilung, die sich auch beim Volltorus ergeben würde. Das heißt konkret: Wenn wir jeweils eine Äquipotentialfläche an den Stirnflächen erzwingen, haben wir tatsächlich im Halbtorus die gleiche Stromdichteverteilung wie im Volltorus. |
Ja.
Auf diese Lösung bin ich letztlich auch gekommen - siehe meinen Beitrag von 11:31. Hattest du den übersehen?
Sorry jedenfalls für die Verwirrung.
|
|
 |
ML
Anmeldungsdatum: 17.04.2013
Beiträge: 3388
|
 ML Verfasst am: 14. Aug 2017 14:13 Titel: ML Verfasst am: 14. Aug 2017 14:13 Titel: |
 |
|
| TomS hat Folgendes geschrieben: |
Auf diese Lösung bin ich letztlich auch gekommen - siehe meinen Beitrag von 11:31. Hattest du den übersehen?
|
Wahrgenommen schon, aber noch nicht gelesen. Aber schön, dass wir uns jetzt einig sind. Es ist immer gut, die (manchmal unausgesprochen) getroffenen Annahmen nochmal zu überprüfen. Wenn wir auf unterschiedlichen Wegen zum gleichen Ergebnis kommen, umso besser.
|
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18016
|
 TomS Verfasst am: 14. Aug 2017 22:12 Titel: TomS Verfasst am: 14. Aug 2017 22:12 Titel: |
 |
|
Ich gebe mal ein paar Zwischenergebnisse für die obige Berechnung an (ich verwende R_T für den Durchmesser des kreisförmigen Drahtes bzw. Torus)

Nun führe ich
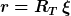
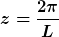
ein.
Das Winkelintegral liefert
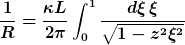
Daraus folgt
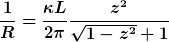
Die Näherung für
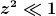
liefert
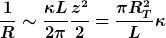
D.h. im Grenzfall eines kleinen Drahtdurchmesser ggü. dem Torusumfang folgt wie erwartet, dass der Widerstandes sich proportional zur Länge L und umgekehrt proportional zur Fläche des Drahtes verhält.
|
|
 |
|
|




















