| Autor |
Nachricht |
ph2010
Gast
|
 ph2010 Verfasst am: 19. Dez 2010 15:19 Titel: Elektrisches Feld im Dielektrikum |
 |
|
Meine Frage:
Es geht um einen Plattenkondensator, der 3 planparallele Dielektrika enthält. Alle 3 Dielektrika haben eine dicke von 0,02m.
Somit ist der Gesamtabstand der beiden Platten 0,06m.
Er1 = 2
Er2 = 3
Er3 = 4
U = 1000V
Welche elektrischen Feldstärken E1, E2 und E3 treten in den einzelnen Dielektrika auf?
Meine Ideen:
Nun ich habe viel überlegt, komme aber nicht auf die angegebenen Lösungen.
Es gilt ja: Eges = Efrei + Egeb
Eges ist das Gesamtfeld im Kondensator
Efrei ist das Feld das von den frei beweglichen Ladungen erzeugt wird.
Egeb ist das Feld das aufgrund der Verschiebung der gebundenen Ladungen entsteht. Also die Ladungen im Dielektrikum.
Nun habe ich mir folgende Formel überlegt: E1 = 1/Er1 * 1000/0,02.
Damit müsste ich das elektrische Feld das im ersten Dielelektrikum auftirtt ausgerechnet haben. Leider komme ich nicht auf das vorgegebene Ergebnis.
Was mache ich nun falsch? |
|
 |
isi1
Anmeldungsdatum: 03.09.2006
Beiträge: 2902
Wohnort: München
|
| isi1 Verfasst am: 19. Dez 2010 16:19 Titel: |
|
|
Gehen wir einfach den geraden Weg,
1. Ladung Q = Cges * U
2. Kapazität Ci = ε0*εi*A/d
Serienschaltung aus drei Kondensatoren: Cges = ε0*A/d * 1/(1/2+1/3+1/4)
3. Dielektrische Verschiebung )
Einsetzen
 ...A kürzen 
_________________
Grüße aus München, isi •≡≈ ¹₁₂½√∠∞±∫αβγδεηκλπρσφω ΔΣΦΩ
Zuletzt bearbeitet von isi1 am 20. Dez 2010 11:11, insgesamt einmal bearbeitet |
|
|
ph2010
Gast
|
| ph2010 Verfasst am: 19. Dez 2010 17:13 Titel: |
|
|
danke für die Antwort, aber was bedeutet bei dir D?
und wie kann ich damit die Feldstärke im Dielektrikum 1 ausrechnen?
Du zeigst ja wie ich die Gesamte Feldstärke ausrechne  |
|
|
GvC
Anmeldungsdatum: 07.05.2009
Beiträge: 14861
|
| GvC Verfasst am: 19. Dez 2010 18:06 Titel: |
|
|
@isi1
Die Feldstärken in den drei Schichten verhalten sich zueinander umgekehrt wie ihre Dielektrizitätszahlen. Welche Feldstärke soll also die von Dir mit E bezeichnete sein?
Nein, hier geht es doch lediglich um den Maschensatz:
U = E1*d/3 + E2*d/3 + E3*d/3 = (E1 + E2 + E3)*d/3
sofern d der Plattenabstand ist.
Mit
und
ergibt sich
\cdot\frac{d}{3})
Damit lässt sich E1 berechnen. Berechnung von E2 und E3 mit Hilfe der obigen Bestimmungsgleichungen. |
|
|
ph2010
Gast
|
| ph2010 Verfasst am: 19. Dez 2010 22:14 Titel: |
|
|
ok, das hilft mir wieter, aber wie komme ich auf die Formeln? Das mit der Maschenregel ist mir klar geworden.
Aber wie bekomme ich die Formel für E2 und E3 heraus? |
|
|
GvC
Anmeldungsdatum: 07.05.2009
Beiträge: 14861
|
| GvC Verfasst am: 20. Dez 2010 10:02 Titel: |
|
|
Die Verschiebungsflussdichte D = Q/A ist in allen drei Schichten gleich groß (gleiche eingeschlossene Ladung Q, gleiche Fläche). Es gilt außerdem
wie sich leicht aus
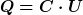
herleiten lässt, und zwar mit Hilfe der im homogenen Feld sehr einfachen Beziehungen
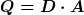
und
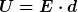
Wenn man sich mit dem elektrostatischen Feld beschäftigt, sollte man die paar Grundgleichungen immer parat haben. |
|
|
isi1
Anmeldungsdatum: 03.09.2006
Beiträge: 2902
Wohnort: München
|
| isi1 Verfasst am: 20. Dez 2010 11:16 Titel: |
|
|
| ph2010 hat Folgendes geschrieben: | danke für die Antwort, aber was bedeutet bei dir D?
und wie kann ich damit die Feldstärke im Dielektrikum 1 ausrechnen?
Du zeigst ja wie ich die Gesamte Feldstärke ausrechne ?( |
D soll die dielektrische Verschiebung sein, die in allen drei Schichten gleich ist.
Und mit D = ε0*εr*E können die einzelnen Feldstärken E errechnet werden.
Ich habs oben ergänzt und verständlicher formuliert.
_________________
Grüße aus München, isi •≡≈ ¹₁₂½√∠∞±∫αβγδεηκλπρσφω ΔΣΦΩ |
|
|
isi1
Anmeldungsdatum: 03.09.2006
Beiträge: 2902
Wohnort: München
|
| isi1 Verfasst am: 20. Dez 2010 11:20 Titel: |
|
|
| GvC hat Folgendes geschrieben: | @isi1
Die Feldstärken in den drei Schichten verhalten sich zueinander umgekehrt wie ihre Dielektrizitätszahlen. Welche Feldstärke soll also die von Dir mit E bezeichnete sein? |
E hatte ich als Feldstärke bei εr=1 gedacht, GvC, die Feldstärke im Dielektrikum wäre dann Ex=E/εrx. Ich wollte dem Fragesteller auch noch etwas übrig lassen - aber es war wohl zu knapp formuliert, wenn schon nicht einmal bekannt ist, dass D die dielektrische Verschiebung sein soll.
Ich habs oben verständlicher formuliert. Stimmen die Ergebnisse mit Deinen überein?
_________________
Grüße aus München, isi •≡≈ ¹₁₂½√∠∞±∫αβγδεηκλπρσφω ΔΣΦΩ |
|
|
GvC
Anmeldungsdatum: 07.05.2009
Beiträge: 14861
|
| GvC Verfasst am: 20. Dez 2010 12:29 Titel: |
|
|
| isi1 hat Folgendes geschrieben: | | Stimmen die Ergebnisse mit Deinen überein? |
Ja. |
|
|
ph2010
Gast
|
| ph2010 Verfasst am: 20. Dez 2010 19:58 Titel: |
|
|
Hallo,
vielen Dank jetzt habe ich es verstanden!
Gibt es auch einen Lösungsweg, wenn man die 3 Schichten als 3 einzelne Kondensatoren betrachtet, ohne den Konendsator als ganzes zu betrachten?
Also ich stelle mir so vor das ich von E1 ausgehend anfange. Und nicht direkt mit Cges rechne.
Leider haben wir in der Vorlesung nichts von dielektrischer Verschiebung bzw. dieser Formel gehört. |
|
|
ph2010
Gast
|
| ph2010 Verfasst am: 20. Dez 2010 20:00 Titel: |
|
|
sry kann nicht editieren als Gast.
C1 ist auch noch bekannt, da vorher schon ausgerechnet.
Also müsste man doch irgendwie E1 direkt ausrechnen können ohne die dielektrische Verschiebung? |
|
|
isi1
Anmeldungsdatum: 03.09.2006
Beiträge: 2902
Wohnort: München
|
| isi1 Verfasst am: 20. Dez 2010 20:13 Titel: |
|
|
| ph2010 hat Folgendes geschrieben: | | sAlso müsste man doch irgendwie E1 direkt ausrechnen können ohne die dielektrische Verschiebung? |
Sicher, denn Wenn Du Cges hast, kannst Du mit Q = C*U = Cges * 1000V ausrechnen, wie viel Ladung jewils in die drei Kondensatoren fließt (es muss ja in jedem der drei Kondensator die gleiche Ladung sein, da die Ladungsträger nicht aus können.
Also wenn Du C1 hast, schreibst einfach C2=2/3 C1, C3 = 2/4 C1
Damit bekommst Du für jeden Kondensator dessen Spannunf U1, U2, U3.
Die Feldstärke ist dann z.B. U3 / d = U3 / 0,02m
Damit kommst Du wieder auf die gleichen Brüche wie bei GvCs und meiner Rechnung.
_________________
Grüße aus München, isi •≡≈ ¹₁₂½√∠∞±∫αβγδεηκλπρσφω ΔΣΦΩ |
|
|
ph2010
Gast
|
| ph2010 Verfasst am: 20. Dez 2010 22:38 Titel: |
|
|
ah perfekt, wieso ich da nicht drauf gekommen bin...
So ist es für mich am einfachsten.
Nur was ich nicht ganz verstehe, am ersten Kondensator müsste doch eigentlich 1000V anliegen oder? Vielleicht habe ich da noch etwas grundlegendes nicht verstanden.
Der Strom fließt ja von + nach minus und am ersten Kondensator müsste doch das volle Potenzial anliegen.
Kann mir da jemand auf die Sprünge helfen? |
|
|
isi1
Anmeldungsdatum: 03.09.2006
Beiträge: 2902
Wohnort: München
|
| isi1 Verfasst am: 21. Dez 2010 00:52 Titel: |
|
|
| ph2010 hat Folgendes geschrieben: | | Nur was ich nicht ganz verstehe, am ersten Kondensator müsste doch eigentlich 1000V anliegen oder? |
Nein, wie GvC schon andeutete, sind die drei Teilkondensatoren (Dielektrika) in Reihe geschaltet, an jedem Teilkondensator kann also nur ein Teil der 1000V anliegen.
Oder vereinfacht: Eine Feldlinie von + nach - muss der Reihe nach durch die drei Dielektrika und an jedem durchläuft sie soviel Spannung wie nötig ist, die Ladung Q durch die Schicht passieren zu lassen.
_________________
Grüße aus München, isi •≡≈ ¹₁₂½√∠∞±∫αβγδεηκλπρσφω ΔΣΦΩ |
|
|
GvC
Anmeldungsdatum: 07.05.2009
Beiträge: 14861
|
| GvC Verfasst am: 21. Dez 2010 10:49 Titel: |
|
|
| ph2010 hat Folgendes geschrieben: | Nur was ich nicht ganz verstehe, am ersten Kondensator müsste doch eigentlich 1000V anliegen oder? Vielleicht habe ich da noch etwas grundlegendes nicht verstanden.
Der Strom fließt ja von + nach minus und am ersten Kondensator müsste doch das volle Potenzial anliegen. |
Du verwechselst Potential und Spannung. Spannung ist eine Potentialdifferenz. Zwar liegt "ganz vorne" das Potential 1000V an. Das ist sozusagen die Potentialdifferenz zwischen dem vorderen Punkt und dem "Endpunkt". Dazwischen gibt es jedoch noch zwei andere Punkte (zwischen Schicht 1 und Schicht 2 sowie zwischen Schicht 2 und Schicht 3). Die haben auch beide ein (jeweils niedrigeres) Potential gegenüber dem Endpunkt (Ende von Schicht 3). Die Spannungen über den einzelnen Schichten sind die jeweiligen Potentialdifferenzen. Keine dieser Potentialdifferenzen kann gleich der anliegenden Gesamtspannung sein, denn erst die Summe aller drei Potentialdifferenzen ist laut Maschensatz gleich der Gesamtspannung von 1000V. |
|
|
ph2010
Gast
|
| ph2010 Verfasst am: 21. Dez 2010 18:49 Titel: |
|
|
| GvC hat Folgendes geschrieben: |
Die Spannungen über den einzelnen Schichten sind die jeweiligen Potentialdifferenzen. Keine dieser Potentialdifferenzen kann gleich der anliegenden Gesamtspannung sein, denn erst die Summe aller drei Potentialdifferenzen ist laut Maschensatz gleich der Gesamtspannung von 1000V. |
Ah natürlich, jetzt verstehe ich das. Wenn man da neu bei der Sache ist, kann das schnell zu Unklarheiten führen wenn U eben auch die Potenzialdifferenz sein kann, wie in diesem Fall.
Vielen Dank noch einmal an dieser Stelle! Damit habt ihr alles gelöst und ich merke ich muss noch viel lernen und das hier gelernte nun verinnerlichen! |
|
|
|
Registrieren
Login
FAQ
Suchen
