| Autor |
Nachricht |
dj2289
Anmeldungsdatum: 31.07.2004
Beiträge: 39
|
 dj2289 Verfasst am: 28. März 2005 18:40 Titel: Pi (Physikalisch) dj2289 Verfasst am: 28. März 2005 18:40 Titel: Pi (Physikalisch) |
 |
|
Hallo,
gibt es eigentlich so etwas wie eine Physikalische PI-konstante ?
Denn rein Physikalisch gesehen, ist Pi ja begrentzt, selbst der kleinste
Kreis besteht aus Atomen ! Also müsste man nur wissen welchen Umfang
ein Atom hat. Stimmt das so ?
_________________
" Wer sich nicht mehr wundern, wer nicht mehr staunen kann, der ist sozusagen tot, sein Auge ist erloschen " Albert Einstein |
|
 |
Nikolas
Ehrenmitglied

Anmeldungsdatum: 14.03.2004
Beiträge: 1873
Wohnort: Freiburg im Brsg.
|
 Nikolas Verfasst am: 28. März 2005 20:04 Titel: Nikolas Verfasst am: 28. März 2005 20:04 Titel: |
 |
|
| Zitat: | Also müsste man nur wissen welchen Umfang
ein Atom hat. Stimmt das so ? |
Was willst du denn mit diesem pi anstellen?
_________________
Nikolas, the mod formerly known as Toxman.
Erwarte das Beste und sei auf das Schlimmste vorbereitet. |
|
 |
mr. black
Moderator

Anmeldungsdatum: 04.07.2004
Beiträge: 228
Wohnort: Krumbach/Österreich
|
 mr. black Verfasst am: 28. März 2005 21:10 Titel: mr. black Verfasst am: 28. März 2005 21:10 Titel: |
 |
|
Wer sagt die, dass ein Atom eine Kugel ist?
Also man darf sich von solchen sachen einfach kein Bild
machen.
Wer sagt, dass Elektronen Teilchen oder gar Kugeln sind?
Das Elektron ist doch nur eine gute Modellvorstellung.
Pi ist einfach nur die Zahl, die den Radius eines Kreises
mit desssen Umfang oder dessen Fläche im Euklidischen
Raum in Beziehung setzt.
Ein Kreis bzw. wie es mir besser gefällt: Eine
Kugel im R² ist definiert als dass jeder Punkt
der Kugel die selbe Entfernung zum Mittlepunkt derer hat.
Es hat nichts mit "dem Gegenstand Physik" zu tun.
|
|
 |
Gast
|
 Gast Verfasst am: 29. März 2005 08:01 Titel: Gast Verfasst am: 29. März 2005 08:01 Titel: |
 |
|
|
Atome sind nicht alle gleich groß, Atome sind nicht unbedingt kugelförmig, Atome sind nicht die kleinsten Elementarteilchen, diese sind auch nicht kreisförmig und deren Größe ist nicht zugänglich. Desweiteren ist der Schluss Kreis besteht aus Atomen, Pi beschränkt schleierhaft. Ein Kreis ist ein mathematisches Konstrukt und hat mit Atomen nichts zu tun und Pi ist nicht nur beschränkt, sondern konstant.
|
|
 |
Nikolas
Ehrenmitglied

Anmeldungsdatum: 14.03.2004
Beiträge: 1873
Wohnort: Freiburg im Brsg.
|
 Nikolas Verfasst am: 29. März 2005 09:27 Titel: Nikolas Verfasst am: 29. März 2005 09:27 Titel: |
 |
|
| Zitat: | | deren Größe ist nicht zugänglich |
Dass würde ich so nicht sagen. Das einfachste, um da eine Vorstellung zu bekommen, ist z.B. Rutherford.
_________________
Nikolas, the mod formerly known as Toxman.
Erwarte das Beste und sei auf das Schlimmste vorbereitet. |
|
 |
Gast
|
 Gast Verfasst am: 29. März 2005 13:18 Titel: Gast Verfasst am: 29. März 2005 13:18 Titel: |
 |
|
Selbst durch tiefinelastische Streuung ist die größe von Quarks nicht zugänglich. Sie sind punktförmig (im experimentellen Sinn), d.h., dass keine Effekte messbar sind, die auf eine Ausdehnung der Quarks zurückzuführen sind.
Aus Quantenchromodynamik folgt (bislang afaik auch "punktförmigkeit" (mit anderer Interpretation).
|
|
 |
Gast
|
 Gast Verfasst am: 29. März 2005 13:45 Titel: Gast Verfasst am: 29. März 2005 13:45 Titel: |
 |
|
Aber rein Theoretisch stimmt das schon was dj2289 geschrieben hat,
allerdings kann man nicht von Atomen ausgehen, sondern muss dies mit
den kleinsten möglichen Teilchen tun.
|
|
 |
Nikolas
Ehrenmitglied

Anmeldungsdatum: 14.03.2004
Beiträge: 1873
Wohnort: Freiburg im Brsg.
|
 Nikolas Verfasst am: 29. März 2005 14:04 Titel: Nikolas Verfasst am: 29. März 2005 14:04 Titel: |
 |
|
| Zitat: | | Aber rein Theoretisch stimmt das schon was dj2289 geschrieben hat, |
Nein, es stimmt nicht. Für den Wert von pi ist es doch völlig uninteressant, dass man damit Kreise berechnen kann, die nicht darstellbar sind.
_________________
Nikolas, the mod formerly known as Toxman.
Erwarte das Beste und sei auf das Schlimmste vorbereitet.
Zuletzt bearbeitet von Nikolas am 29. März 2005 19:56, insgesamt einmal bearbeitet |
|
 |
Mister S

Anmeldungsdatum: 06.01.2005
Beiträge: 426
|
 Mister S Verfasst am: 29. März 2005 14:06 Titel: Mister S Verfasst am: 29. März 2005 14:06 Titel: |
 |
|
|
Wie kommt ihr denn darauf, das Pi begrenzt ist, nur weil es keine unendlich kleinen Kreise gibt? Pi gibt das Verhältnis von Durchmesser und Umfang eines Kreises an. Da die Länge als Physikalische Einheit nicht gequantelt ist, ist Pi ja nicht automatisch endlich, sondern es ist ausdrücklich möglich, dass Pi eine unendliche Zahl von Nachkommastellen hat. Zumal auch etwa Wurzel 2 eine nicht endliche Zahl von Nachkommastellen hat, obwohl diese Zahl eine physikalisch sinnvolle Definition hat (Länge der Diagonalen des Einheitsquadrats).
|
|
 |
Gast
|
 Gast Verfasst am: 29. März 2005 17:16 Titel: Gast Verfasst am: 29. März 2005 17:16 Titel: |
 |
|
Hallo, hier sind grad mehrere Gäste unterwegs, den Mist mit "aber rein theoretisch" habe ich nicht geschrieben 
@Mister S: Begrenzt im Sinne von "Grenzwert von Funktionen/Folgen/etc." hat nichts mit der Anzahl der Nachkommastellen zu tun. Wurzel 2 ist eine stinknormale reelle Zahl und genau so "endlich" wie  . .
|
|
 |
Mister S

Anmeldungsdatum: 06.01.2005
Beiträge: 426
|
 Mister S Verfasst am: 29. März 2005 19:38 Titel: Mister S Verfasst am: 29. März 2005 19:38 Titel: |
 |
|
|
Dann versteh ich nicht, was ihr meint.
|
|
 |
dachdecker2
Administrator

Anmeldungsdatum: 15.06.2004
Beiträge: 1174
Wohnort: Zeppelinheim / Hessen
|
 dachdecker2 Verfasst am: 29. März 2005 20:26 Titel: dachdecker2 Verfasst am: 29. März 2005 20:26 Titel: |
 |
|
Wurzel aus zwei ist so weit ich weiss irrational, nicht reell. Das gleiche trifft auf Pi und seine Vielfache zu.
_________________
Gruß, dachdecker2
http://rettedeinefreiheit.de |
|
 |
bishop
Moderator

Anmeldungsdatum: 19.07.2004
Beiträge: 1133
Wohnort: Heidelberg
|
 bishop Verfasst am: 29. März 2005 20:39 Titel: bishop Verfasst am: 29. März 2005 20:39 Titel: |
 |
|
Irrational ist in der Reellen Zahlenmenge mit drin^^
_________________
Ein Physiker ist jemand, der über die ersten drei Terme einer divergenten Reihe mittelt |
|
 |
dachdecker2
Administrator

Anmeldungsdatum: 15.06.2004
Beiträge: 1174
Wohnort: Zeppelinheim / Hessen
|
 dachdecker2 Verfasst am: 29. März 2005 22:35 Titel: dachdecker2 Verfasst am: 29. März 2005 22:35 Titel: |
 |
|
Reelle Zahlen können als Brüche zweier ganzer Zahlen geschrieben werden. Das trifft auf Pi (meines Wissens nach sind über 10^12 Stellen bekannt) und auf viele Wurzeln nicht zu. Reelle Zahlen sind in Dezimaldarstellung (Kommazahl sozusagen) mit einer endlichen Zahl an nichtperiodischen Stellen ausgestattet (irgendwann wird es periodisch oder geht mit 000.. weiter).
_________________
Gruß, dachdecker2
http://rettedeinefreiheit.de |
|
 |
Nikolas
Ehrenmitglied

Anmeldungsdatum: 14.03.2004
Beiträge: 1873
Wohnort: Freiburg im Brsg.
|
 Nikolas Verfasst am: 29. März 2005 22:40 Titel: Nikolas Verfasst am: 29. März 2005 22:40 Titel: |
 |
|
| Zitat: | | Reelle Zahlen können als Brüche zweier ganzer Zahlen geschrieben werden. |
Waren das nicht die rationalen Zahlen?
_________________
Nikolas, the mod formerly known as Toxman.
Erwarte das Beste und sei auf das Schlimmste vorbereitet. |
|
 |
bishop
Moderator

Anmeldungsdatum: 19.07.2004
Beiträge: 1133
Wohnort: Heidelberg
|
 bishop Verfasst am: 29. März 2005 22:42 Titel: bishop Verfasst am: 29. März 2005 22:42 Titel: |
 |
|
doch^^
Es gibt übrigens mehr irrationale zahlen als rationale, und davon sinds ja schon unendlich viele 
_________________
Ein Physiker ist jemand, der über die ersten drei Terme einer divergenten Reihe mittelt |
|
 |
dachdecker2
Administrator

Anmeldungsdatum: 15.06.2004
Beiträge: 1174
Wohnort: Zeppelinheim / Hessen
|
|
 |
dachdecker2
Administrator

Anmeldungsdatum: 15.06.2004
Beiträge: 1174
Wohnort: Zeppelinheim / Hessen
|
 dachdecker2 Verfasst am: 29. März 2005 22:45 Titel: dachdecker2 Verfasst am: 29. März 2005 22:45 Titel: |
 |
|
Unendlich viele Elemente haben aber alle (Grund-)Zahlenmengen  , weil alle außer den irrationalen Zahlen (oder?) auf der Mange N, die auch unendlich viele Elemente hat, aufbauen. , weil alle außer den irrationalen Zahlen (oder?) auf der Mange N, die auch unendlich viele Elemente hat, aufbauen.
_________________
Gruß, dachdecker2
http://rettedeinefreiheit.de |
|
 |
Nikolas
Ehrenmitglied

Anmeldungsdatum: 14.03.2004
Beiträge: 1873
Wohnort: Freiburg im Brsg.
|
 Nikolas Verfasst am: 29. März 2005 22:50 Titel: Nikolas Verfasst am: 29. März 2005 22:50 Titel: |
 |
|
Unendlich wird ja erst interessant, wenn man dann die Mächtigkeiten vom Mengen vergleicht und dann sagt, dass im Intervall [0;1] so viele reele Zahlen wie im Intervall ]0;1[ sind. Oder wenn man Mengen dann auf abzählbarkeit überprüft
_________________
Nikolas, the mod formerly known as Toxman.
Erwarte das Beste und sei auf das Schlimmste vorbereitet. |
|
 |
bishop
Moderator

Anmeldungsdatum: 19.07.2004
Beiträge: 1133
Wohnort: Heidelberg
|
 bishop Verfasst am: 29. März 2005 22:58 Titel: bishop Verfasst am: 29. März 2005 22:58 Titel: |
 |
|
jop zum Beispiel ist die Mächtigkeit der Menge der ganzen Zahlen kleiner als die der Brüche, weil es schon unendlich viele Brüche im Intervall [0;1] gibt, die Menge der ganzen Zahlen in diesem Intervall aber nur zwei Elemente enthält. Ähnlich verhält es sich mit den transzendenten Zahlen wie 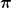 und und 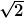
_________________
Ein Physiker ist jemand, der über die ersten drei Terme einer divergenten Reihe mittelt |
|
 |
Nikolas
Ehrenmitglied

Anmeldungsdatum: 14.03.2004
Beiträge: 1873
Wohnort: Freiburg im Brsg.
|
 Nikolas Verfasst am: 29. März 2005 23:11 Titel: Nikolas Verfasst am: 29. März 2005 23:11 Titel: |
 |
|
| Zitat: | | jop zum Beispiel ist die Mächtigkeit der Menge der ganzen Zahlen kleiner als die der Brüche, weil es schon unendlich viele Brüche im Intervall [0;1] gibt, die Menge der ganzen Zahlen in diesem Intervall aber nur zwei Elemente enthält |
Das ist leider falsch.
Zwei Mengen sind dann gleichmächtig, wenn eine bijective Zuordnungsvorschrift existiert.
Nimm dir einfach einen Zahlenstrahl nach rechts und beschrifte ihn mit den Zahlen aus N (>0), das gleiche nach oben.
Jetzt denkst du dir senkrechte und waagrechte Linien durch alle Zahlen und hast ein regelmäßiges Gitter. An die Kreuzungspunkte schreibst du jetzt die Brüche die sich aus den Randzahlen ergeben (Siehe Anhang)
Jetzt kannst du dich auf einem festgelegten Weg durch diese Brüche durcharbeiten und triffst so sicher auf alle Brüche. Die Brüche nummerierst du durch und schon hast du deine bijective Funktion und den Beweis dass N und Q gleich mächtig sind.
| Beschreibung: |
|
| Dateigröße: |
2.62 KB |
| Angeschaut: |
6288 mal |
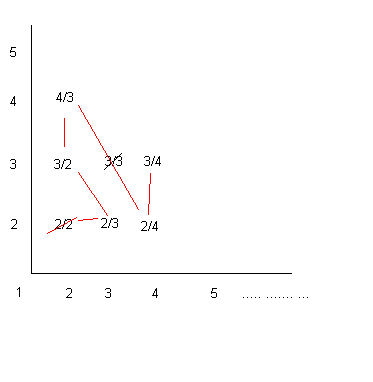
|
_________________
Nikolas, the mod formerly known as Toxman.
Erwarte das Beste und sei auf das Schlimmste vorbereitet. |
|
 |
bishop
Moderator

Anmeldungsdatum: 19.07.2004
Beiträge: 1133
Wohnort: Heidelberg
|
 bishop Verfasst am: 29. März 2005 23:20 Titel: bishop Verfasst am: 29. März 2005 23:20 Titel: |
 |
|
Und was ist, wenn du dir nur die Anzahl der Elemente im Intervall [0;1] anschaust? Du zählst wieviele ganze Zahlen sich in dem Intervall befinden (2 wenn ich das richtig sehe^^) und wieviele Dezimalzahlen (etwas mehr, wenn ich das richtig sehe^^) Ich sage nicht, dass du unrecht hast, nur ist imo die "Auflösung" Gitters zu niedrig, wenn ich das richtig sehe.
_________________
Ein Physiker ist jemand, der über die ersten drei Terme einer divergenten Reihe mittelt |
|
 |
Nikolas
Ehrenmitglied

Anmeldungsdatum: 14.03.2004
Beiträge: 1873
Wohnort: Freiburg im Brsg.
|
 Nikolas Verfasst am: 29. März 2005 23:22 Titel: Nikolas Verfasst am: 29. März 2005 23:22 Titel: |
 |
|
wie willst du denn die Auflösung erhöhen?
Nimm dir doch mal altternativ die Frage ob es mehr reele Zahlen oder reele Zahlen im Intervall [0;1] gibt, diese Mengen sind auch gleich mächtig, obwohl die eine eine echte Teilmenge der anderen ist. Einfach so mit anzählen gehts leider nicht.
_________________
Nikolas, the mod formerly known as Toxman.
Erwarte das Beste und sei auf das Schlimmste vorbereitet. |
|
 |
bishop
Moderator

Anmeldungsdatum: 19.07.2004
Beiträge: 1133
Wohnort: Heidelberg
|
 bishop Verfasst am: 29. März 2005 23:31 Titel: bishop Verfasst am: 29. März 2005 23:31 Titel: |
 |
|
meines Wissenstandes nach ist die bijektive Projektion eine Operation, bei der man versucht jedem Element einer Menge ein Element einer anderen Menge zu zu ordnen. Ist das gelungen so sind die beiden Mengen gleich mächtig. Okay nun schauen wir uns die Menge der Ganzen Zahlen an. Diese beinhaltet die Zahlen 1,2,3,4,5... und ihre negativen Pendants. Zu jeder Zahl n lässt sich ein weiteres Element mit Hilfe der Zuordnung n+1 konstruieren. Die Menge der Rationalen Zahlen beinhaltet auch dezimalzahlen welche als ein Bruch zweier ganzer Zahlen geschrieben werden können. Nun ich kann zwar dem Element 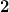 der Menge der ganzen Zahlen das Element der Menge der ganzen Zahlen das Element 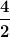 zuweisen, ich finde aber kein äquivalentes Element der ganzen Zahlen, das ich dem Bruch zuweisen, ich finde aber kein äquivalentes Element der ganzen Zahlen, das ich dem Bruch 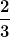 zuweisen könnte. Das ist für mich ein Beweis, dass die Menge der Rationalen Zahlen mächtiger als die Menge der Ganzen Zahlen ist zuweisen könnte. Das ist für mich ein Beweis, dass die Menge der Rationalen Zahlen mächtiger als die Menge der Ganzen Zahlen ist
_________________
Ein Physiker ist jemand, der über die ersten drei Terme einer divergenten Reihe mittelt |
|
 |
Nikolas
Ehrenmitglied

Anmeldungsdatum: 14.03.2004
Beiträge: 1873
Wohnort: Freiburg im Brsg.
|
 Nikolas Verfasst am: 29. März 2005 23:36 Titel: Nikolas Verfasst am: 29. März 2005 23:36 Titel: |
 |
|
Die Liste beginnt so:
1 -> 1/1
2 -> 2/1
3 -> 1/2
4 -> 3/1
5 -> 3/2
usw. einfach mal aufmalen und durchzeichnen. Im Endeffekt hast du da eine schöne Zuordnung. Die will ich zwar nicht exolizit angeben müssen, aber wenn es eine rekursive gibt, reicht das ja auch.
| Zitat: | | Das ist für mich ein Beweis, dass die Menge der Rationalen Zahlen mächtiger als die Menge der Ganzen Zahlen ist |
Für mich aber nicht 
_________________
Nikolas, the mod formerly known as Toxman.
Erwarte das Beste und sei auf das Schlimmste vorbereitet. |
|
 |
bishop
Moderator

Anmeldungsdatum: 19.07.2004
Beiträge: 1133
Wohnort: Heidelberg
|
 bishop Verfasst am: 29. März 2005 23:42 Titel: bishop Verfasst am: 29. März 2005 23:42 Titel: |
 |
|
Moment du hast es doch gerade eben selbst gezeigt oder? oO
Nach 5 Schritten bist du bei den Ganzen Zahlen bei 5, bei den Rationalen Zahlen aber erst bei 3/2, welches sich dezimal als 1,5 ausschreiben lässt. Das heisst, dass die Menge der Ganzen Zahlen "vorgeht" und quasi schneller auf die Unendlichkeit zustrebt, als die Rationalen Zahlen. 
_________________
Ein Physiker ist jemand, der über die ersten drei Terme einer divergenten Reihe mittelt |
|
 |
Nikolas
Ehrenmitglied

Anmeldungsdatum: 14.03.2004
Beiträge: 1873
Wohnort: Freiburg im Brsg.
|
 Nikolas Verfasst am: 29. März 2005 23:44 Titel: Nikolas Verfasst am: 29. März 2005 23:44 Titel: |
 |
|
Und dann bleiben die natürlichen Zahlen an der Unendlichkeits-Grenze hängen? Klingt etwas komisch, genau wie die Frage nach der [0;1]- Intervall in den reelen Zahlen, ist aber wirklich so 
_________________
Nikolas, the mod formerly known as Toxman.
Erwarte das Beste und sei auf das Schlimmste vorbereitet. |
|
 |
bishop
Moderator

Anmeldungsdatum: 19.07.2004
Beiträge: 1133
Wohnort: Heidelberg
|
 bishop Verfasst am: 29. März 2005 23:53 Titel: bishop Verfasst am: 29. März 2005 23:53 Titel: |
 |
|
das nicht, aber sie sind eben früher da...
hmm ich versuche das mal Anschaulich zu machen..
Wir haben zwei Gefässe. Wir wissen nicht, wie viel sie fassen, sehen aber, dass das eine ein viel grösseren Durchmesser hat, vermuten also, dass es mehr Volumen hat, könnn das aber nicht abmessen oder berechnen. Wir füllen die Gefässe also zu bestimmten Bruchteilen der Höhe, sagen wir 1/3, 1/4, und 1/2 und berechnen dann das Volumen des Wassers. Wenn die Wassermenge bei einem Gefäss stets höher ist als bei dem anderen schliessen wir darauf, dass dieses mehr fasst ohne dass wir implizit das Volumen messen mussten. Das ist doch der Satz von Avocardo oder wie der auch hiess, das kann man auch auf die Menge verwenden.
_________________
Ein Physiker ist jemand, der über die ersten drei Terme einer divergenten Reihe mittelt |
|
 |
Nikolas
Ehrenmitglied

Anmeldungsdatum: 14.03.2004
Beiträge: 1873
Wohnort: Freiburg im Brsg.
|
 Nikolas Verfasst am: 29. März 2005 23:57 Titel: Nikolas Verfasst am: 29. März 2005 23:57 Titel: |
 |
|
| Zitat: | | Wir füllen die Gefässe also zu bestimmten Bruchteilen der Höhe, sagen wir 1/3, 1/4, und 1/2 und berechnen dann das Volumen des Wassers. |
Wie füllst du ein Gefäß unbekannter Höhe zu Hälfze mit Wasser?
_________________
Nikolas, the mod formerly known as Toxman.
Erwarte das Beste und sei auf das Schlimmste vorbereitet. |
|
 |
bishop
Moderator

Anmeldungsdatum: 19.07.2004
Beiträge: 1133
Wohnort: Heidelberg
|
 bishop Verfasst am: 30. März 2005 00:02 Titel: bishop Verfasst am: 30. März 2005 00:02 Titel: |
 |
|
hmh na gut sagen wir ich fülle es eine bestimmte höhe vom Boden ab, so ging der Satz nämlich, dass zwei Körper genau dann dasselbe Volumen haben, wenn ihre Querschnittsfläche für jedes h gleich gross ist. Ich gehe zwar vom Volumen aus, ist aber dasselbe wenn ich vorraussetze, dass die zwei Gefässe einfache Prismen sind
_________________
Ein Physiker ist jemand, der über die ersten drei Terme einer divergenten Reihe mittelt |
|
 |
AndyRo
Anmeldungsdatum: 27.12.2004
Beiträge: 22
Wohnort: Hamburg
|
 AndyRo Verfasst am: 30. März 2005 02:21 Titel: AndyRo Verfasst am: 30. März 2005 02:21 Titel: |
 |
|
| Zitat: | Ähnlich verhält es sich mit den transzendenten Zahlen wie 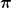 und und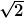 |
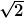 ist keine transzendente Zahl! ist keine transzendente Zahl!
MfG: AndyRo
_________________
- Wenn alle Stricke reißen, dann hänge ich mich auf - (Karl Krauss) |
|
 |
bishop
Moderator

Anmeldungsdatum: 19.07.2004
Beiträge: 1133
Wohnort: Heidelberg
|
 bishop Verfasst am: 30. März 2005 09:39 Titel: bishop Verfasst am: 30. März 2005 09:39 Titel: |
 |
|
oki habs nachgesehen, hast recht, ich hatte ein anderes Verständnis für die transzendenten Zahlen, es ändert aber nur minimal etwas an der Sache.
€dit: Hoffe das genügt in dieser Diskussion:
| Zitat: | | Im Jahr 1874 konnte Georg Cantor nicht nur abermals die Existenz von transzendenten Zahlen beweisen, sondern sogar zeigen, dass es "mehr" transzendente als algebraische Zahlen gibt. Im Gegensatz zu Liouville sicherte Cantor aber seine Erkenntnisse durch einen indirekten Beweis. Die mathematisch exakte Formulierung des Begriffs "mehr" war aber sicherlich das wichtigste Ergebnis von Cantors Arbeit, weil es das Wissen über das reelle Zahlensystem revolutionär vertiefte. Allerdings konnten sich seine neuartigen Ideen gegen einflussreiche konservative Kritiker wie Leopold Kronecker lange Zeit nicht durchsetzen. Er bewies, dass die Menge der algebraischen reellen Zahlen (in moderner Sprechweise) abzählbar ist, während die Menge aller reellen Zahlen überabzählbar (unendlich, aber nicht abzählbar) ist. Daraus folgt auch leicht, dass die Menge aller transzendenten Zahlen gleichmächtig mit der Menge aller reellen Zahlen (insbesondere: ebenfalls überabzählbar) ist. |
etwas weiter unten:
| Zitat: | Dieses kuriose Resultat, nämlich dass eine echte Teilmenge von 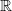 die gleiche Mächtigkeit haben kann wie die gleiche Mächtigkeit haben kann wie  selbst, konnte Cantor durch die Benutzung von Bijektionen erklären. selbst, konnte Cantor durch die Benutzung von Bijektionen erklären. |
€dit2:
und ach ja hier noch was:
| Zitat: | 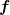 ist bijektiv, wenn für alle ist bijektiv, wenn für alle 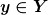 genau ein genau ein 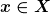 mit mit  = y) existiert. existiert.
(genau eins bedeutet eins und nur eins) |
Nun das ist bei den Ganzen und den Rationalen Zahlen nicht gegeben, da ich der Ganzen Zahl 1 unendlich viele Brüche zuweisen könnte wie 2/2, 3/3, 4/4 etc...
_________________
Ein Physiker ist jemand, der über die ersten drei Terme einer divergenten Reihe mittelt |
|
 |
SheepTrick

Anmeldungsdatum: 07.03.2005
Beiträge: 99
|
 SheepTrick Verfasst am: 30. März 2005 10:41 Titel: SheepTrick Verfasst am: 30. März 2005 10:41 Titel: |
 |
|
|
Es ist egal, wie voll Du das Gefäß mit der größeren Querschnittsfläche machst, Du kannst den Inhalt immer vollständig in das Gefäß mit der kleineren Querschnittsfläche kippen, ohne daß etwas überschwappt. Und so ähnlich argumentieren die Mathematiker auch,daß die Mengen Q und N gleich mächtig sind.
|
|
 |
Nikolas
Ehrenmitglied

Anmeldungsdatum: 14.03.2004
Beiträge: 1873
Wohnort: Freiburg im Brsg.
|
 Nikolas Verfasst am: 30. März 2005 11:00 Titel: Nikolas Verfasst am: 30. März 2005 11:00 Titel: |
 |
|
@ Bishop:
Du stellts dir in dieser Zuweisungsfunktion irgendwie immer nur eine Umformung einer Zahl vor. Die Brüche werden einfach nur in eine sinnvolle Reihenfolge gebracht und dann abgezählt. Ob dann die 5 aus N der 5/1 aus Q oder der 3/2 aus Q zugeordnet wird, ist uninteressant. Es geht nur darum zu zeigen, dass es eine Möglichkeit gibt, alle Brüche in eine Reihenfolge zu bringen.
| Zitat: | | Nun das ist bei den Ganzen und den Rationalen Zahlen nicht gegeben, da ich der Ganzen Zahl 1 unendlich viele Brüche zuweisen könnte wie 2/2, 3/3, 4/4 etc... |
Stimmt das könntest du und hättest damit keine bijektive Funktion gebildet. Aber nur weil deine Funktion nicht bijektiv ist, muss das ja nicht heissen, dass es keine gibt.
_________________
Nikolas, the mod formerly known as Toxman.
Erwarte das Beste und sei auf das Schlimmste vorbereitet. |
|
 |
bishop
Moderator

Anmeldungsdatum: 19.07.2004
Beiträge: 1133
Wohnort: Heidelberg
|
 bishop Verfasst am: 30. März 2005 11:24 Titel: bishop Verfasst am: 30. März 2005 11:24 Titel: |
 |
|
@Sheep:
Das Argument zieht nicht, ich kanns nämlich nicht andersrum machen, also würde ich das Grössere Gefäss in das kleinere umkippen würde es überlaufen. Und wenn du sagst, dass beide Gefässe unendlich hoch sind, so würde das Wasser im kleineren Gefäss höher stehen.
@tox:
Ich würde einfach über diese Definition der bijektivität fahren, wenn ich eine Folge konstruieren kann, die nicht bijektiv ist nach dieser Definition, so können die zwei Mengen nicht bijektiv und somit gleichmächtig sein. Ob es eine gibt interessiert mich ja nicht, ich will doch das Gegenteil beweisen^^
_________________
Ein Physiker ist jemand, der über die ersten drei Terme einer divergenten Reihe mittelt |
|
 |
Nikolas
Ehrenmitglied

Anmeldungsdatum: 14.03.2004
Beiträge: 1873
Wohnort: Freiburg im Brsg.
|
 Nikolas Verfasst am: 30. März 2005 11:56 Titel: Nikolas Verfasst am: 30. März 2005 11:56 Titel: |
 |
|
| Zitat: |
Ich würde einfach über diese Definition der bijektivität fahren, wenn ich eine Folge konstruieren kann, die nicht bijektiv ist nach dieser Definition, so können die zwei Mengen nicht bijektiv und somit gleichmächtig sein. |
Das ist aber falsch.
Ich nehme mal die Mengen 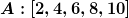 und und 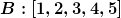 . Man kann gerade noch an einer Hand anzählen, dass die beiden Mengen gleichmächtig sind. . Man kann gerade noch an einer Hand anzählen, dass die beiden Mengen gleichmächtig sind.
Jetzt nehm ich die Funktion =1) Damit bilde ich alle Elemente aus A auf die 1 in B ab. Nach deiner Argumentation ein Beweis für die Nichtgleichmächtigkeit von A und B. Damit bilde ich alle Elemente aus A auf die 1 in B ab. Nach deiner Argumentation ein Beweis für die Nichtgleichmächtigkeit von A und B.
Aber z.B. die Funktion =a/2) ist bijektiv ist bijektiv =2b \ ] ) und beweist so, dass A und B gleichmächtig sind. und beweist so, dass A und B gleichmächtig sind.
Deine Argumentation ist also falsch.
_________________
Nikolas, the mod formerly known as Toxman.
Erwarte das Beste und sei auf das Schlimmste vorbereitet. |
|
 |
SheepTrick

Anmeldungsdatum: 07.03.2005
Beiträge: 99
|
 SheepTrick Verfasst am: 30. März 2005 12:04 Titel: SheepTrick Verfasst am: 30. März 2005 12:04 Titel: |
 |
|
| bishop hat Folgendes geschrieben: | @Sheep:
Das Argument zieht nicht, ich kanns nämlich nicht andersrum machen, also würde ich das Grössere Gefäss in das kleinere umkippen würde es überlaufen. Und wenn du sagst, dass beide Gefässe unendlich hoch sind, so würde das Wasser im kleineren Gefäss höher stehen. |
Aber genau das ist doch egal. Ein Gefäß in dem das Wasser höher steht als in einem anderen, kann doch trotzdem genausoviel fassen. (Könnte sogar mehr fassen) 
Gleichmächtige Mengen zeichnen sich dadurch aus, daß Du für jedes Element ein Element in der anderen Menge findest. Dir "gehen nie die Elemente aus". Oder in Deinem Beispiel: Da schwappt nie was über.
|
|
 |
dachdecker2
Administrator

Anmeldungsdatum: 15.06.2004
Beiträge: 1174
Wohnort: Zeppelinheim / Hessen
|
 dachdecker2 Verfasst am: 30. März 2005 13:14 Titel: dachdecker2 Verfasst am: 30. März 2005 13:14 Titel: |
 |
|
Deswegen hat Toxman ja auch das bild oben gemalt. Wenn alle Brüche nummeriert sind, hat man eine eineindeutige Zuordnungsvorschrift, um aus Natürlichen Zahlen Rationale zu machen und umgekerht. Diese Zuordnungsvorschrift dürfte zwar ziehmlich schwer mathematisch zu formulieren sein, aber das ist nicht von Bedeutung. Für jede Nummer (natürliche Zahlen) gibt es genau eine einzige rationale Zahl.
aber ich hab noch eine Frage: Was bedeutet eigentlich das Wort "Mächtigkeit"? Ist N0 mächtiger als N? Aus dem Text, der sich in den vorangegangenen Posts verteilt, schließe ich, dass N und N0 gleich mächtig sind, obwohl N0 offensichtlich ein Element mehr enthählt als N. Richtig?
_________________
Gruß, dachdecker2
http://rettedeinefreiheit.de |
|
 |
Nikolas
Ehrenmitglied

Anmeldungsdatum: 14.03.2004
Beiträge: 1873
Wohnort: Freiburg im Brsg.
|
 Nikolas Verfasst am: 30. März 2005 13:21 Titel: Nikolas Verfasst am: 30. März 2005 13:21 Titel: |
 |
|
2 Mengen sind dann gleich mächtig, wenn eine solche bijektive Zuordnungsvorschrift existiert. N0 und N sind gliechmachtig, weil ich mir der Funktion  = n+1 ) die Mengen bijektiv aufeinander Abbilden kann. die Mengen bijektiv aufeinander Abbilden kann.
_________________
Nikolas, the mod formerly known as Toxman.
Erwarte das Beste und sei auf das Schlimmste vorbereitet. |
|
 |
dachdecker2
Administrator

Anmeldungsdatum: 15.06.2004
Beiträge: 1174
Wohnort: Zeppelinheim / Hessen
|
 dachdecker2 Verfasst am: 30. März 2005 13:25 Titel: dachdecker2 Verfasst am: 30. März 2005 13:25 Titel: |
 |
|
Wie muss ich mir eine solche bijektive Zuordnungsvorschrift vorstellen, wenn es für die Zahlen der zu vergleichenden Mengen keine "Nachfolger" definiert sind? Etwa bei den Reellen zahlen ist das der Fall. Oder gibt es eine Vorschrift, die mir den Nachfolger von 1 im Bereich der reellen Zahlen bestimmt?
_________________
Gruß, dachdecker2
http://rettedeinefreiheit.de |
|
 |
|