| Autor |
Nachricht |
ahmedhos
Anmeldungsdatum: 18.06.2010
Beiträge: 10
|
|
 |
Fabian2206
Anmeldungsdatum: 16.01.2010
Beiträge: 53
Wohnort: Prüm
|
 Fabian2206 Verfasst am: 18. Jun 2010 20:09 Titel: |
 |
|
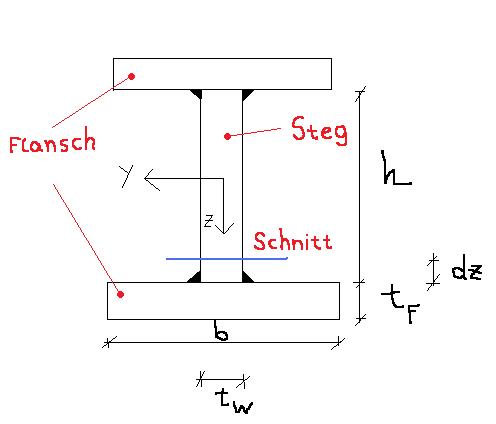
"Das Statische Moment, oder auch Flächenmoment 1. Grades, wird immer auf den Schwerpunkt bezogen berechnet. Es ist im Schwerpunkt am größten und in den am weitesten vom Schwerpunkt entferntesten differentiell kleinen Teilflächen am Kleinsten bzw. Null. Die Berechnung erfolgt analog der eines Momentes, nämlich: Summe aus Teilflächen mal achsenbezogener Abstand aus Teilflächenschwerpunkt zu Gesamtschwerpunkt (Summe aus Kraft mal Hebelarm). Es sind immer mindestens zwei Statische Momente in einem Querschnitt vorhanden. "
Auszug aus:
http://www.offroad-travel.de/conewa/Technik/Doku/Allgemeiner_Ueberblick_Querschnittskennwerte.html
In deinem Link wurde aber nicht einfach das Statische Moment berechnet oder? Den es wird noch durch eine größe klein s geteilt, welche ebenfalls die Dimension "cm" haben muss da sonst ein Einheitenfehler vorliegt.
EDIT: Hier hat jemand genauso ein I-Profil durchgerechnet:
http://www.t-l-net.de/t-l-downloads/querschnittswerte.pdf
|
|
|
ahmedhos
Anmeldungsdatum: 18.06.2010
Beiträge: 10
|
|
|
ahmedhos
Anmeldungsdatum: 18.06.2010
Beiträge: 10
|
| ahmedhos Verfasst am: 23. Jun 2010 07:42 Titel: Hallo, |
|
|
Ich fand bis zum heutigen Tag in keinem Buch, das ich in der Hand genommen habe, eine Integration bei solchen Problemen. Allerdings bin ich fest davon überzeugt, daß es funktioniert, deshalb frag ich und hoffe auf eine gut Antwort dazu. Danke schön.
lg
Ahmed
|
|
|
VeryApe
Anmeldungsdatum: 10.02.2008
Beiträge: 3247
|
|
|
VeryApe
Anmeldungsdatum: 10.02.2008
Beiträge: 3247
|
| VeryApe Verfasst am: 23. Jun 2010 10:53 Titel: |
|
|
Warum keiner über ein Rechteck integriert dürfte wohl klar sein.
P=\int z * dA = z * k * dz= k*z² * 0.5= k *z *z *0.5)
|
|
|
ahmedhos
Anmeldungsdatum: 18.06.2010
Beiträge: 10
|
|
|
VeryApe
Anmeldungsdatum: 10.02.2008
Beiträge: 3247
|
| VeryApe Verfasst am: 23. Jun 2010 21:24 Titel: |
|
|
| ahme.... hat Folgendes geschrieben: |
Ok, du willst also die Kreiskurve mit der Kreisgleichung mathematisch erfassen
|
hm, du wolltest doch wissen wie man mittels integrationsmethode ermittelt.
P=\int z (r-\sqrt {r²-z²}) *dz )
Integration durch Substitution
z=sin u
Das hast du nun zu integrieren, kannsd du integrieren?
wenn ja dann bitte tus, dann hast du das statische Moment.
Wie du es dann auf deinen gewollten Ursprung verschiebst hab ich dir ja auch geschrieben.
Denn die Integrationsmethode liefert dir das statische Moment auf den Kreismittelpunktursprung in z Richtung. mußt also nur noch die Ages * Verschiebelänge rechnen.
um was gehts hier denn hast du nur keine Ahnung wie man die Funktion zum Integrieren aufstellt oder kannsd du gar nicht integrieren.
ersteres hab ich dir ja bereit gestellt.
|
|
|
ahmedhos
Anmeldungsdatum: 18.06.2010
Beiträge: 10
|
| ahmedhos Verfasst am: 24. Jun 2010 08:58 Titel: Hallo, |
|
|
Jeder zweite Schüler kann mittlerweile integrieren. Aber verstehen kann ich deine Methode nicht. Besonders die komischen (A_100 bis A_10000000000). Außerdem mußt du zuerstmal überhaupt ein Integralausdruck zum Leben rufen ("Mit den sogenannten Integrationsgrenzen. Kennst du sie überhaupt?"), damit man "integrieren" kann.
(Denn die Integrationsmethode liefert dir das statische Moment auf den Kreismittelpunktursprung in z Richtung. mußt also nur noch die Ages * Verschiebelänge rechnen.)
Aber so will ich das nicht machen. Ich würde gern alles auf mein gezeichnetes y,z-Koordinatensystem beziehen.
(um was gehts hier denn hast du nur keine Ahnung wie man die Funktion zum Integrieren aufstellt oder kannsd du gar nicht integrieren.)
Wenn du nicht weißt, um was es hier geht, warum antwortest du denn?
peace.
Ahmed
Zuletzt bearbeitet von ahmedhos am 24. Jun 2010 12:22, insgesamt 3-mal bearbeitet |
|
|
ahmedhos
Anmeldungsdatum: 18.06.2010
Beiträge: 10
|
|
|
ahmedhos
Anmeldungsdatum: 18.06.2010
Beiträge: 10
|
|
|
ahmedhos
Anmeldungsdatum: 18.06.2010
Beiträge: 10
|
|
|
VeryApe
Anmeldungsdatum: 10.02.2008
Beiträge: 3247
|
| VeryApe Verfasst am: 24. Jun 2010 23:35 Titel: |
|
|
| Zitat: | Jeder zweite Schüler kann mittlerweile integrieren. Aber verstehen kann ich deine Methode nicht. Besonders die komischen (A_100 bis A_10000000000). Außerdem mußt du zuerstmal überhaupt ein Integralausdruck zum Leben rufen ("Mit den sogenannten Integrationsgrenzen. Kennst du sie überhaupt?"), damit man "integrieren" kann.
|
Also zum Integrieren braucht man keine Integrationsgrenzen. Diese braucht man wenn ich die Wertdifferenz der Stammfunktion bestimmen will die die Fläche der Ableitungsfunktion darstellt.
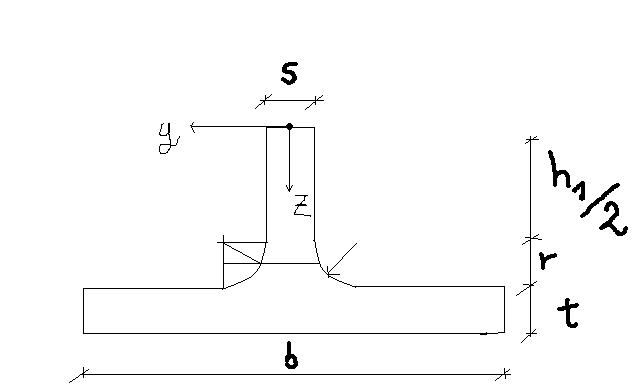
Das diese nur von 0 bis r gehen kann, kann man ja in meiner Skizze erkennen.
auf dein Koordinatensystem umgeschrieben
=\int (z+0.5 \cdot h_{1}) (r-\sqrt {r²-z²}) *dz )
mit integrationsgrenzen
=\int^{r}_{0} (z+0.5 \cdot h_{1}) (r-\sqrt {r²-z²}) *dz )
Auf deine gewollte Ausrundungsfläche, die aber den Ausrundungen entspricht plus die innere Fläche von s \cdot r.
=2 \cdot \int^{r}_{0} (z+0.5 \cdot h_{1}) (r-\sqrt {r²-z²}) *dz + s \cdot r \cdot (r*0.5 +h_{1} \cdot 0.5))
Das die meisten der Mittelstufe Schüler integrieren können kann sein, aber anscheinend wissen die meisten nicht das das mit Flächenbildung vergleichbar ist, die Umkehrung einer Steigungsbildung ist die Flächenbildung.
| ahme... hat Folgendes geschrieben: |
(um was gehts hier denn hast du nur keine Ahnung wie man die Funktion zum Integrieren aufstellt oder kannsd du gar nicht integrieren.)
Wenn du nicht weißt, um was es hier geht, warum antwortest du denn?
denn ich bin anscheinend doch nicht so falsch gelegen das du das nicht integrieren kannsd siehe.
|
um was es hier geht weiß ich eigentlich, nur ist mir dein Wissen nicht bekannt und ob du nur nen Ansatz brauchst oder alles.
| ahme.. hat Folgendes geschrieben: |
^2} \, dz
<br />
)
Will mir jemand helfen und sich an I herantasten?
|
Immerhin weiß ich jetzt das du das nicht integrieren kannsd.
Also du wolltest Ansatz plus Integration.
Aber es ist immerhin auch nicht so leicht und zeitaufwendig, das hier zu schreiben.
ich zeig dir das anhand meiner Gleichung und wenn du lieber die hergeleitete Formel von Matheboard angehen willsd, vielleicht zeigt dir das ein anderer oder du probierst es mal selber, wenn du das hier verstanden hast.
 (r-\sqrt {r²-z²}) *dz )
 (1-\sqrt {1-(\frac {z}{r})²}) *dz )
Integration durch Substitution:
z=r*sin u
 (1-\sqrt {1-(\frac {r \cdot sinu}{r})²}) *r \cdot cos u \cdot du )
 (1-\sqrt {1- sin²u}) \cdot cos u \cdot du )
 (1-cos u) \cdot cos u \cdot du )
 \cdot du )
 + 0.5 \cdot h_{1} (\int cos u - \int cos² u) \cdot du )
********************************
Produktintegration:
*********************************
b'=sin u c= cos u
b=- cos u c'= -sin u
************************
b'=sin u c= cos² u
b=- cos u c'=- 2 cos u * sin u
***************************************
b'=cos u c= cos u
b=sin u c'= -sin u
 * du)
****************************
+ 0.5 \cdot h_{1} (sin u - \frac {sin u \cdot cos u + u}{2})] )
+ 0.5 \cdot h_{1} \cdot (sin u - \frac {sin u \cdot cos u + u}{2})] )
 )
Grenzen z=0 und z=r
=0 )
=0.5 \pi )
=\cdot \int^{z=r}_{z=0} (z+0.5 \cdot h_{1}) (r-\sqrt {r²-z²}) *dz =\cdot \int^{u=0.5 \pi}_{u=0} r² \cdot [r \cdot cos²u \cdot (\frac {cos u}{3} - 0.5)+ 0.5 \cdot h_{1} \cdot (sin u - \frac {sin u \cdot cos u + u}{2})])
cos 0.5 pi=0 cos 0=1
sin 0.5 pi= 1 sin 0 =0
=0.5 \cdot h_{1} \cdot r² \cdot (1- 0.25 \pi) - r³ (\frac {1}{3} -0.5) )
**********************************************
Statisches Moment einer Ausrundung.
=h_{1} \cdot r² \cdot (0.5- 0.125 \pi) +\frac {1}{6} r³ )
**********************************************
Für deinen Ausrundungsteil kommt hier noch das statische Moment der inneren Fläche hinzu also s*r (0.5 r + 0.5 h1) =0.5 s*r (r+h1)
=2 [ h_{1} \cdot r² \cdot (0.5- 0.125 \pi) +\frac {1}{6} r³]+ 0.5 \cdot s \cdot r \cdot (r+h_{1})
<br />
)
Zuletzt bearbeitet von VeryApe am 25. Jun 2010 13:42, insgesamt 3-mal bearbeitet |
|
|
ahmedhos
Anmeldungsdatum: 18.06.2010
Beiträge: 10
|
| ahmedhos Verfasst am: 25. Jun 2010 10:14 Titel: Hallo, |
|
|
Leider helfen mir deine Tipps wenig. Mir gehts darum das Integral im Beitrag 9 zu loesen. Aber jemand wird schon helfen. Vielleicht in 2020. Ich bin ein Optimist und habs nicht eilig. Eigentlich ist es mir ziemlich egal, ob es ueberhaupt geloest wird. Das brauche ich naemlich nicht. Nur mein Neugier nach Wissen. Nutzloses Wissen macht bekanntlich Spass. Ausserdem denke ich, dass es mit der Physik sowas von vorbei ist. Es geht lediglich um ein Integral. Wenn ichs echt gern wissen will, wie man das Integral hinkriegt, dann frage ich auf ein Matheforum und nicht hier.
Also Bitte 
lg
Ahmed
|
|
|
VeryApe
Anmeldungsdatum: 10.02.2008
Beiträge: 3247
|
| VeryApe Verfasst am: 25. Jun 2010 20:35 Titel: |
|
|
gg SPAM du kannsd ja die gleiche Substitution verwenden nur mit 05h1 erweitern und die Integrale für cosu sinu und cosu gleich weiter verwenden
und im Endeffekt erhälst du dasselbe wie ich,
hättest dir also die Integration selbst erarbeiten können-
aber du hast Recht sowas solltest du im Mathe Forum erfragen, hat wenig mit Physik zu tun.
MFG
|
|
|
|
Registrieren
Login
FAQ
Suchen
