| Autor |
Nachricht |
soa
Anmeldungsdatum: 25.09.2005
Beiträge: 73
|
 soa Verfasst am: 29. Jun 2008 14:40 Titel: Energie im schwingenden System soa Verfasst am: 29. Jun 2008 14:40 Titel: Energie im schwingenden System |
 |
|
Hallo,
ich hätte da noch einmal eine Frage zur folgenden Aufgabe:
An einer (im folgenden als masselos angenommenen) Schraubenfeder ist ein Körper befestigt. Er führt ungedämpfte harmonische Schwingungen aus. m = 300 g ; T = 2 s ; Eges = 0,2 J
Berechnen Sie die maximale Amplitude der Masse.
Meine Frage nun : Beschreibt sich die Gesamtenergie desPendels zu
W = mgh mit h = ymax ?
oder ist W = Wkin + Wpot
W= 1/2 mv² + 1/2 Ds² nach v auflösen und dann einsetzen in
v wäre dann y0 * w und Ergebns in y = ymax sin(wt)
Welche Vorgehensweise wäre hier die Richtige ?
Danke |
|
 |
soa
Anmeldungsdatum: 25.09.2005
Beiträge: 73
|
 soa Verfasst am: 30. Jun 2008 12:29 Titel: soa Verfasst am: 30. Jun 2008 12:29 Titel: |
 |
|
Also ich meine , dass sich die Schwingungsenergie aus
Wkin = 1/2 mv² zusammensetzt.
Es wäre schön, wenn ich wüßte die sich Eges. berechnet.
Vielen Dank im Voraus. |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 30. Jun 2008 12:34 Titel: dermarkus Verfasst am: 30. Jun 2008 12:34 Titel: |
 |
|
Die Gesamtenergie ist die Summe aus kinetischer und potentieller Energie.
Magst du mal sagen, zu welchem Zeitpunkt die kinetische Energie maximal und die potentielle Energie Null ist?
Und zu welchem anderen Zeitpunkt die potentielle Energie maximal und die kinetische Energie Null ist?
Hilft dir das, um auf einfache Weise einen Zeitpunkt zu wählen, zu dem du besonders leicht die Gesamtenergie berechnen kannst? |
|
 |
soa
Anmeldungsdatum: 25.09.2005
Beiträge: 73
|
 soa Verfasst am: 30. Jun 2008 12:45 Titel: soa Verfasst am: 30. Jun 2008 12:45 Titel: |
 |
|
Also ist die Gesamt Energie immer
W = 1/2 mv² + 1/2 Ds²
kinetiasche Energie Maximum bei der Feder: wenn die Federlänge = Federlänge +s , also wenn die Feder absolut gedehnt ist. Oder beim Durchgang durch den Ruhepunkt ?
Bei einem Pendel würde die Kinetische Energie ein Maximum bei T/2 haben, also dort wo das Gewicht auf einer Höhe mit der Aufhängung ist ? |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 30. Jun 2008 13:34 Titel: dermarkus Verfasst am: 30. Jun 2008 13:34 Titel: |
 |
|
| soa hat Folgendes geschrieben: |
kinetiasche Energie Maximum bei der Feder: wenn die Federlänge = Federlänge +s , also wenn die Feder absolut gedehnt ist. Oder beim Durchgang durch den Ruhepunkt ?
|
Na, welches von beiden?
Tipp: Wo ist der schwingende Körper an der Feder am schnellsten? |
|
 |
soa
Anmeldungsdatum: 25.09.2005
Beiträge: 73
|
 soa Verfasst am: 30. Jun 2008 16:41 Titel: soa Verfasst am: 30. Jun 2008 16:41 Titel: |
 |
|
Ok. also beim Durchgang durch den Ruhepunkt ist v = max
In der Dehnung wird v irgenwann ja null.
Aber den Dreh zur Gesamtenergie sehe ich noch nicht.. |
|
 |
Nubler
Anmeldungsdatum: 04.06.2008
Beiträge: 120
|
 Nubler Verfasst am: 30. Jun 2008 16:59 Titel: Nubler Verfasst am: 30. Jun 2008 16:59 Titel: |
 |
|
wie hängt die gesamtenergie explizit von der zeit ab?
was folgt daraus? |
|
 |
soa
Anmeldungsdatum: 25.09.2005
Beiträge: 73
|
 soa Verfasst am: 30. Jun 2008 18:29 Titel: soa Verfasst am: 30. Jun 2008 18:29 Titel: |
 |
|
Ja, ich würde sagen, dass die Schwingungen kleiner werden und Energie verloren geht. Je größer t, desto größer der Energieverlust.
Was folgt daraus ? -- Weiß nicht genau worauf du hinaus willst.
Habe das hier gefunden:
Die Gesamtenergie des Körpers ist konstant und darauf bezogen, dass die Lageenergie im Nulldurchgang gleich Null ist, gilt:
E = mgh
Anscheinend scheint sich die Gesamtenergie durch mgh zu berechnen mit h = ymax ...
So ganz kann ich das nichnachvollziehen  |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 30. Jun 2008 18:36 Titel: dermarkus Verfasst am: 30. Jun 2008 18:36 Titel: |
 |
|
| soa hat Folgendes geschrieben: | Ok. also beim Durchgang durch den Ruhepunkt ist v = max
|
Einverstanden 
Den Nullpunkt für die potentielle Energie (h=0) würde ich in den Ruhepunkt, also in die Gleichgewichtslage der Feder mit Gewicht dran setzen. Dann ist die potentielle Energie beim Nulldurchgang gleich Null.
Also ist dann die Gesamtenergie der Schwingung gleich der kinetischen Energie im Nulldurchgang. Kannst du diese kinetische Energie im Nulldurchgang berechnen? |
|
 |
soa
Anmeldungsdatum: 25.09.2005
Beiträge: 73
|
 soa Verfasst am: 30. Jun 2008 19:12 Titel: soa Verfasst am: 30. Jun 2008 19:12 Titel: |
 |
|
Also im Nulldurchgang ist die potentielle Energie = 0. Un die kinetische Enerige berechnet sich zu E = 1/2 mv² . Das ist die Schwingungsenergie.
Die kinetische Energie erreicht Ihr Maximum, wenn die potentielle Energie gleich Null ist .
Jedoch ist die Energie (kin u. pot ) immer von der Amplitude abhängig.
Bei einer harmonischen Schwingung bleibt die Energie konstant, da reibungsfrei.
Die Gesamtenergie ist dann die potentielle Energie, die zu Beginn der Schwingung in das System gesteckt wurde.
Also : Eges = m * g * ymax
OK? |
|
 |
soa
Anmeldungsdatum: 25.09.2005
Beiträge: 73
|
 soa Verfasst am: 30. Jun 2008 19:19 Titel: soa Verfasst am: 30. Jun 2008 19:19 Titel: |
 |
|
Vielleicht noch einmal Präzise:
Energie der Schwingung: E = 1/2 mv²
Gsamtenergie des schw. Systems: E = mgh.
Kann man das so sagen ? |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 01. Jul 2008 12:58 Titel: dermarkus Verfasst am: 01. Jul 2008 12:58 Titel: |
 |
|
Bei der Feder ist die potentielle Energie nicht einfach gleich Hubenergie, weil es bei der Feder ja die Spannenergie gibt.
Möchtest du daher die Gesamtenergie der schwingenden Feder nicht viel einfacher aus dem Zeitpunkt berechnen, zu dem alle Energie kinetische Energie ist? |
|
 |
soa
Anmeldungsdatum: 25.09.2005
Beiträge: 73
|
 soa Verfasst am: 01. Jul 2008 18:53 Titel: soa Verfasst am: 01. Jul 2008 18:53 Titel: |
 |
|
Hallo,
Also ich benötige die Geschwindigkeit im Nulldurchgang. Das ist mein vmax. Wenn v also vmax , dann
ergibt sich E = 1/2 mv²
Ich hoffe, dass stimmt soweit.
----------------------------------------------------
Nehmen wir einmal diese Aufgabe:
Eine Masse wird zwischen zwei Federn mit D1 und D2 gespannt. Die Masse wird um x nach rechts ausgelenkt und losgelassen.
D1 / D2 /m / x gegeben.
Dann wäre x meine maximale Amplitude. Wäre hier
E = m g ymax richtig ?
VG
SOA |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 01. Jul 2008 18:57 Titel: dermarkus Verfasst am: 01. Jul 2008 18:57 Titel: |
 |
|
| soa hat Folgendes geschrieben: |
Also ich benötige die Geschwindigkeit im Nulldurchgang. Das ist mein vmax. Wenn v also vmax , dann
ergibt sich E = 1/2 mv²
Ich hoffe, dass stimmt soweit.
|
Einverstanden 
| soa hat Folgendes geschrieben: |
[...] Wäre hier
E = m g ymax richtig ?
|
Nein.
Denn die potentielle Energie in Federn ist ja Spannenergie und nicht Lageenergie. Also musst du natürlich die Formel für die Spannenergie nehmen und nicht die Formel für die Lageenergie. |
|
 |
soa
Anmeldungsdatum: 25.09.2005
Beiträge: 73
|
 soa Verfasst am: 01. Jul 2008 19:40 Titel: soa Verfasst am: 01. Jul 2008 19:40 Titel: |
 |
|
Also wäre E wäre demnach:
Eges = 1/2 D1s² + 1/2 D2s²
Und kann ich dann die Formel W = mgh völlig vergessen ?
Was ist mit dieser Aussage:
Die Gesamtenergie des Körpers ist konstant und darauf bezogen, dass die Lageenergie im Nulldurchgang gleich Null ist, gilt: E = mgh
Vielen Dank |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 01. Jul 2008 20:20 Titel: dermarkus Verfasst am: 01. Jul 2008 20:20 Titel: |
 |
|
Ich glaube, du fragst hier letztendlich nach fertigen Formeln, mit denen du diese Sorte von Aufgaben rechnen kannst, und hast auf der anderen Seite noch nicht so recht verstanden, was diese Sorte Aufgabe dir beibringen möchte bzw. welchen Lernstoff diese Aufgaben abfragen.
Natürlich kannst du erstmal alle möglichen Energien für so ein schwingendes Federsystem aufschreiben.
Wenn du dabei aber den Nullpunkt der potentiellen Energie geschickt wählst, dann werden auch diese komplizierten aussehenden Aufgaben wieder so einfach wie ein ganz normaler Federschwinger, bei dem die Energie immer zwischen Spannenergie und kinetischer Energie hin- und her umgewandelt wird.
So dass die Gesamtenergie bezüglich dieses Energienullpunktes
* beim Nulldurchgang gleich der kinetischen Energie 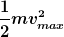 ist ist
* und an den Stellen maximaler Auslenkung gleich der Spannenergie 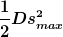 ist ist
Was dabei das 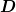 , das , das 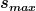 , das , das 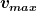 und der Energienullpunkt (der liegt am besten dort, wo die kinetische Energie der harmonischen Federschwingung maximal ist) ist, findest du je nach Aufgabe sehr leicht heraus, oder aber du musst dir dazu ein bisschen genauer all die zugehörigen Formeln zusammenstellen und betrachten. und der Energienullpunkt (der liegt am besten dort, wo die kinetische Energie der harmonischen Federschwingung maximal ist) ist, findest du je nach Aufgabe sehr leicht heraus, oder aber du musst dir dazu ein bisschen genauer all die zugehörigen Formeln zusammenstellen und betrachten.
------------------------
Magst du am besten mal eine konkrete Aufgabe aussuchen, und um die zu lösen dazusagen, was du in diesem Zusammenhang bereits in der Vorlesung gelernt hast? |
|
 |
soa
Anmeldungsdatum: 25.09.2005
Beiträge: 73
|
 soa Verfasst am: 03. Jul 2008 13:03 Titel: soa Verfasst am: 03. Jul 2008 13:03 Titel: |
 |
|
OK.
Eine Masse mit 50 g wird horizontal zwischen 2 Federn gespannt und kann reibungsfrei gleiten. Sie wird um 30 cm nach rechts ausgelenkt und dann losgelassen.
D1 = 20 N/m D2 = 30 D/m
Gesucht : E gesamt
s wären doch 0,3 m ?
D gesamt = D1 + D2 = 50 N/m
F1 = -F2
m* g = D * s
s = (m*g) / D // ich nehme gleich D gesamt
s = 0.0981 m // Das ist Käse...
E = D s² mit Dgesamt und smax
E = 50 N/m * 0,3 m = 4,5 J
Sind 4,5 J korrekt ?
Vielen Dank |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 03. Jul 2008 16:40 Titel: dermarkus Verfasst am: 03. Jul 2008 16:40 Titel: |
 |
|
Die 4,5 J sind nicht korrekt.
Zur Erinnerung: Die Formel für die Spannenergie einer Feder mit Federkonstante D, die um die Strecke s ausgelenkt wird, heißt
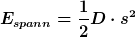
* Zeichne dir mal die Situation laut Aufgabenstellung auf. Siehst du dann, dass die Gewichtskraft nichts mit dieser Aufgabe zu tun hat?
* Woher hast du die Information, die Vermutung oder das Wissen genommen, dass die Gesamtfederkonstante dieser Anordnung gleich der Summe der beiden einzelnen Federkonstanten sei? Bist du dir mit dieser Ausage bereits sicher?
Falls nein, würde ich empfehlen, dass du dir das ganze einfach mal ohne der Verwendung dieser Information ausführlich aufschreibst und schaust, was für eine Gesamtfederkonstante dabei herauskommt. |
|
 |
soa
Anmeldungsdatum: 25.09.2005
Beiträge: 73
|
 soa Verfasst am: 04. Jul 2008 07:28 Titel: soa Verfasst am: 04. Jul 2008 07:28 Titel: |
 |
|
Hallo Markus,
bezüglich D Gesamt habe ich die folgende Argumentation:
Die potentielle Energie eines schwingenden Systems ist an 2 Punkten maximal:
In der vollkommenden Dehnung der Feder und in der vollkommenen Stauchung. Die beiden Punkte bilden Minimum und Maximum der Kurve.
Bei der maximalen Auslenkung des Wagens hat die eine Feder ein Minimum und die Andere ein Maximum. Beide Federn wirken also hier mit Ihren Kräften.
Das sich die Federn subtrahieren kann ich mir nicht vorstellen. Laut meinen Aufzeichnungen addieren sich die Federn...
Entschuldige meinen Fauxpas mit der Spannenergie, die ich wirklich bei 2,25 J vermute.
Nachtrag zu D: Wenn D ges = D1 + D2 , dann ich v von links nach rechts genauso schnell wie von rechts nach links.
Wie siehst Du das denn ?
Vielen Dank. |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 04. Jul 2008 11:15 Titel: dermarkus Verfasst am: 04. Jul 2008 11:15 Titel: |
 |
|
Mit den 2,25 J bin ich einverstanden 
Wenn in deinen Aufzeichnungen steht, dass die Gesamtfederkonstante in dieser Situation gleich der Summe der beiden Federkonstanten ist, dann haben deine Aufzeichnungen Recht.
Mit deiner Herleitung in Worten komme ich allerdings noch nicht auf diesen Zusammenhang.
Ich würde den Zusammenhang hier durch Hinschreiben der konkreten Formeln herleiten:
Ist das System in Ruhe und im Gleichgewicht, dann hat die Feder 1 mit 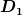 die Auslenkung die Auslenkung 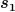 und die Feder 2 mit und die Feder 2 mit 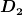 die Auslenkung die Auslenkung 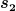 , also ist die Energie dann , also ist die Energie dann
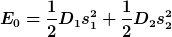
und beide Federkräfte sind gleich stark:
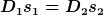 . .
Lenkt man das System nun um A=30 cm aus, dann wächst die Auslenkung der einen Feder um A, und die Auslenkung der anderen Feder sinkt um A, und die Energie ist gleich
^2 + \frac{1}{2}D_2(s_2 - A)^2 \\ &=& \underbrace{\frac{1}{2}D_1s_1^2 + \frac{1}{2}D_2 s_2^2}_{=E_0} + A \underbrace{(D_1 s_1 - D_2 s_2)}_{=0} + \frac{1}{2}D_1 A^2 + \frac{1}{2}D_2 A^2 \\ &=& E_0 + \frac{1}{2}(D_1+D_2) A^2)
Man wählt 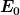 als Nullpunkt der potentiellen Energie und bekommt als Energie der Schwingung als Nullpunkt der potentiellen Energie und bekommt als Energie der Schwingung
}_{D_{\rm ges}}A^2)
und man sieht, dass hier in der Tat  ist. ist. |
|
 |
soa
Anmeldungsdatum: 25.09.2005
Beiträge: 73
|
 soa Verfasst am: 04. Jul 2008 12:28 Titel: soa Verfasst am: 04. Jul 2008 12:28 Titel: |
 |
|
Hallo Markus,
ich danke Dir. 
Das wirft nun allerdings wieder fragen auf. Woher nimmst du das A aus deiner Formel?
und : D1 = 20 N/m D2 = 30 D/m
In der Aufgabe habe ich unterschiedliche Werte für D.
Ist es egal, ob D1 = D2 ist oder < > D2 , ist dann D1s = D2s und ist
Dges. = D1 + D2 immer zutreffend ?
Viele Grüße |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 04. Jul 2008 16:09 Titel: dermarkus Verfasst am: 04. Jul 2008 16:09 Titel: |
 |
|
Magst du meine Herleitung gerne noch mal in Ruhe durchgehen, um sie nachzuvollziehen? Ich glaube, ich habe so ziemlich alles dazugeschrieben, was nötig ist, um sie für dich nachvollziehbar zu machen.
Magst du dir mal eine Skizze machen, in der du das zeichnest, was in ich Form von Worten, Variablenbezeichnungen und Formeln in dieser Herleitung geschrieben habe, und diese Skizze hier zeigen?
Ich habe ganz bewusst keinen der drei Abstände, die ich verwendet habe, einfach nur mit  bezeichnet, um Verwirrungen und Verwechslungen zu vermeiden und die Variablenbezeichnungen aussagekräftig und eindeutig zu machen. bezeichnet, um Verwirrungen und Verwechslungen zu vermeiden und die Variablenbezeichnungen aussagekräftig und eindeutig zu machen. |
|
 |
soa
Anmeldungsdatum: 25.09.2005
Beiträge: 73
|
 soa Verfasst am: 05. Jul 2008 11:41 Titel: soa Verfasst am: 05. Jul 2008 11:41 Titel: |
 |
|
Ich habe in der Tat nur flüchtig gelesen. Es steht ja alles da.
A ist die Auslenkung
und in der Ruhelage ist D1s1 = D2s2 ...
Ich danke Dir. |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 05. Jul 2008 12:56 Titel: dermarkus Verfasst am: 05. Jul 2008 12:56 Titel: |
 |
|
Ich glaube, ich habe auch noch eine Idee für dich, wie du das 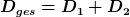 für die Anordnung der Federn in dieser Aufgabe auch direkt mit dem zeigen kannst, was du hier für die Anordnung der Federn in dieser Aufgabe auch direkt mit dem zeigen kannst, was du hier
| soa hat Folgendes geschrieben: |
Die potentielle Energie eines schwingenden Systems ist an 2 Punkten maximal:
In der vollkommenden Dehnung der Feder und in der vollkommenen Stauchung. Die beiden Punkte bilden Minimum und Maximum der Kurve.
Bei der maximalen Auslenkung des Wagens hat die eine Feder ein Minimum und die Andere ein Maximum. Beide Federn wirken also hier mit Ihren Kräften.
Das sich die Federn subtrahieren kann ich mir nicht vorstellen. Laut meinen Aufzeichnungen addieren sich die Federn...
|
angefangen hast, zu formulieren. Schaffst du es, ein ) -Diagramm zu zeichnen, das die Kraft -Diagramm zu zeichnen, das die Kraft ) der ersten Feder auf die schwingende Masse, die Kraft der ersten Feder auf die schwingende Masse, die Kraft ) der zweiten Feder auf die schwingende Masse und die Gesamtkraft der zweiten Feder auf die schwingende Masse und die Gesamtkraft =F_1(x) + F_2(x)) auf die schwingende Masse als Funktionen der Position auf die schwingende Masse als Funktionen der Position  der schwingenden Masse aufzutragen? Und magst du dieses Diagramm mal hier zeigen? der schwingenden Masse aufzutragen? Und magst du dieses Diagramm mal hier zeigen? |
|
 |
|


















