| Autor |
Nachricht |
frage1
Anmeldungsdatum: 20.02.2021
Beiträge: 569
Wohnort: bayern
|
 frage1 Verfasst am: 22. Mai 2022 07:54 Titel: Wanddruck, Druckänderung |
 |
|
Hallo alle!
Es handelt sich um den mikroskopischen Druck eines Gases auf die Wand. Ich soll hier folgendes berechnen:
a) Wie ändert sich der Druck, wenn sich bei konst. Teilchendichte, die mittlere Geschwindigkeit der Teilchen verdoppelt?
b) Wie ändert sich p, wenn bei konst. mittlerer Teilchengeschwindigkeit, die Masse des Teilchens verdoppelt wird?
Die Lösungen sind: a) p= 4 p b) p= 2p
Ich kann ehrlich gesagt nicht einschätzen, ob ich die Aufgabe verstanden habe. Der Druck hängt ja von der Masse, Dichte und der mittleren quadr. Geschw. der Teilchen ab, demzufolge muss ich ja die Formel P=1/3 N m v^2 verwenden. Bei a) müsste dann die Berechnung folgendermaßen aussehen: 1/3 N m * 4 v^2, oder? Dann müsste ja für p= 4/3 rauskommen? Denke ich da falsch?
Also so stelle ich mir das ganze vor:
| Beschreibung: |
|
| Dateigröße: |
21.81 KB |
| Angeschaut: |
967 mal |
|
|
|
 |
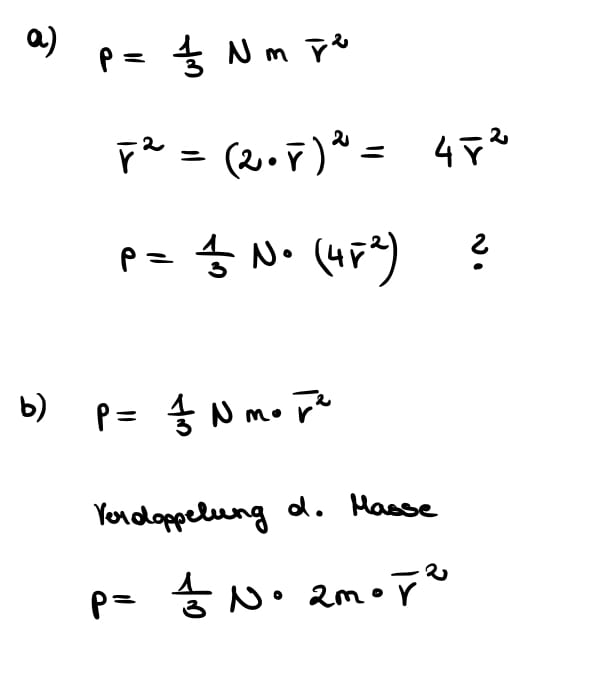
Füsik-Gast
Gast
|
| Füsik-Gast Verfasst am: 22. Mai 2022 10:41 Titel: Druck |
|
|
du hast die Formel für den Gasdruck im Teilchenmodell gegeben,wo u.a. die Masse und die Geschwindigkeit der Gasteilchen als Faktoren enthalten sind.
Man muß hier einfach schauen,wie der Druck von den jweiligen Faktoren abhängt,dabe sind Exponenten zu berücksichtigen.
Bei der Masse m ist der Esponent 1,daher bewirkt eine Verdopplung der Masse allein auch nur eine Verdopplung des Drucks.
Die Geschwindigkeit geht jedoch quadratisch ein(Exponent 2),daher wird eine Verdopplung von v zu einer Vervierfachung führen(2 hoch 2).
Wie sähe es bei einer Verdreifachung von v aus?
Füsik-Gast.
|
|
|
frage1
Anmeldungsdatum: 20.02.2021
Beiträge: 569
Wohnort: bayern
|
| frage1 Verfasst am: 22. Mai 2022 16:57 Titel: |
|
|
Erstmal danke für deine Antwort Füsik-Gast!
Bei einer verdreifachung von v^2 kämen wir auf eine versechsfachung, weil (v^2)^3 = v^6, also der druck nimmt dann zu, oder?
Was noch unklar ist: Warum betrachten wir hier nur die exponenten? Ich hätte einfach für die mittlere geschw. die zahl 2 eingesetzt, also 2*v^2 gerechnet, das stimmt ja so nicht, aber wieso? ich kann mir noch nicht erklären, warum mein Ansatz falsch ist
|
|
|
as_string
Moderator
Anmeldungsdatum: 09.12.2005
Beiträge: 5785
Wohnort: Heidelberg
|
| as_string Verfasst am: 23. Mai 2022 00:17 Titel: |
|
|
Nein, die Abhängigkeit von p von der mittleren Geschwindigkeit ist quadratisch und von der Masse linear. Wenn sich die mittlere Geschwindigkeit verdoppelt während die Masse gleich bleibt hast Du 2^2=4-fachen Druck, bei dreifacher mittl. Geschwindigkeit 3^2=9-fachen Druck.
Wenn Du m festhältst und v variierst, verhält sich das ganze doch wie eine Parabel und wenn Du die Geschwindigkeit fest hältst und m variierst, wie eine Ursprungsgerade.
Gruß
Marco
|
|
|
Aruna
Anmeldungsdatum: 28.07.2021
Beiträge: 795
|
| Aruna Verfasst am: 23. Mai 2022 06:08 Titel: |
|
|
| frage1 hat Folgendes geschrieben: | Erstmal danke für deine Antwort Füsik-Gast!
Bei einer verdreifachung von v^2 kämen wir auf eine versechsfachung, weil (v^2)^3 = v^6, also der druck nimmt dann zu, oder? |
Ja, der Druck nimmt zu. Die Frage ist allerdings, um wie viel der Druck zu nimmt.
In der Frage von Füsik-Gast verdreifacht sich nicht  sondern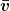 
Eine Funktion, die quadratisch von v abhängt, versechsfacht sich dann nicht
sondern nimmt um den Faktor  zu
Bei konstanter Masse und Teilchenzahl folgt bei Verdreifachung der mittleren Geschwindigkeit also für den Druck:
| frage1 hat Folgendes geschrieben: |
Was noch unklar ist: Warum betrachten wir hier nur die exponenten? Ich hätte einfach für die mittlere geschw. die zahl 2 eingesetzt, also 2*v^2 gerechnet, das stimmt ja so nicht, aber wieso? ich kann mir noch nicht erklären, warum mein Ansatz falsch ist |
Dein Ansatz ganz oben hat gestimmt.
Der Exponent bleibt 2 und Du schaust, wie sich der Exponent auf den Faktor auswirkt.
Also nicht 2*v^2 sondern (2*v)^2 = 4*v^2 wie es auch in Deiner (?) Rechnung im Eingangsbeitrag steht.
Du solltest allerdings den Druck vorher und nachher, (z.B. durch Indizes 1, 2 ) unterscheiden, wenn Du ein Gleichheitszeichen hinschreibst.
Das geht schon bei der Angabe der Lösung los:
| frage1 hat Folgendes geschrieben: |
Die Lösungen sind: a) p= 4 p b) p= 2p
|
Diese Gleichungen sind nur für p=0 richtig.
Ansonsten kann ich die durch p teilen und erhalte 1=4 bzw. 1=2
Also besser:
 p_2 = 4p_1 )
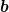 p_2 = 2p_1)
Desgleichen in Deiner Rechnung bezüglich v.
Da schreibst Du:
^2 = 4 \bar{v}^2)
für  kommt dann wieder 1=4 raus
| frage1 hat Folgendes geschrieben: | Bei a) müsste dann die Berechnung folgendermaßen aussehen: 1/3 N m * 4 v^2, oder? Dann müsste ja für p= 4/3 rauskommen? Denke ich da falsch?
|
Nein, Du denkst IMO nicht falsch, schreibst Deine Gedanken aber falsch hin:
Es kommt  raus.
Der Faktor 1/3 steckt ja auch schon in p_1
Also: wenn sich die Geschwindigkeit von v_1 auf v_2 ändert, gilt:
mit  folgt:
^2 = \frac{1}{3}Nm (2^2) \bar{v_1}^2 = 4( \frac{1}{3} Nm \bar{v_1}^2) = 4 p_1 )
p= 4/3 kommt nur raus, wenn p vorher 1/3 war, also N=1, m=1 und v=1 und alles dimensionslos.
|
|
|
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5852
|
| Myon Verfasst am: 23. Mai 2022 08:25 Titel: |
|
|
Nur eine Bemerkung: In der Gleichung für den Druck tritt nicht  auf, sondern  , also die mittlere quadratische Geschwindigkeit. An der Antwort auf die Frage ändert sich nichts, denn wenn v Maxwell-Boltzmann-verteilt ist, stehen die beiden Grössen in einem konstanten Verhältnis.
|
|
|
|
|
Registrieren
Login
FAQ
Suchen
