| Autor |
Nachricht |
MarkoOoooooo84
Anmeldungsdatum: 13.01.2022
Beiträge: 1
|
 MarkoOoooooo84 Verfasst am: 13. Jan 2022 17:13 Titel: Energie im diskreten und kontinuierlichem Spektrum MarkoOoooooo84 Verfasst am: 13. Jan 2022 17:13 Titel: Energie im diskreten und kontinuierlichem Spektrum |
 |
|
Meine Frage:
Hallo,
kann es in der Quantenmechanik vorkommen, dass der Energieeigenwert im diskreten und kontinuierlichem Spektrum vorkommt? Wie rechnet man in diesem Fall die Lösung der zeitabhängigen Schrödingergleichung aus, wenn solche Energien vorliegen ?
Vielen Dank im Voraus!
Meine Ideen:
keine Idee |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 13. Jan 2022 18:05 Titel: Re: Energie im diskreten und kontinuierlichem Spektrum TomS Verfasst am: 13. Jan 2022 18:05 Titel: Re: Energie im diskreten und kontinuierlichem Spektrum |
 |
|
| MarkoOoooooo84 hat Folgendes geschrieben: | | ... kann es in der Quantenmechanik vorkommen, dass der Energieeigenwert im diskreten und kontinuierlichem Spektrum vorkommt? Wie rechnet man in diesem Fall die Lösung der zeitabhängigen Schrödingergleichung aus, wenn solche Energien vorliegen ? |
Wenn die Schrödingergleichung sowohl ein diskretes als auch ein kontinuierliches Spektrum hat, dann ist offenbar
\,u_E(x) = 0)
 = \sigma_p(H) \cup \sigma_c(H))
Die rechts stehenden Terme bezeichnen das diskrete oder Punktspektrum, d.h. diskrete Eigenwerte mit normierbaren Eigenfunktionen, sowie das kontinuierliche Spektrum mit nicht-normierbaren "verallgemeinerten" Eigenfunktionen.
Dabei gilt in den mir bekannten Fällen immer
 < \sigma_c(H) = (0,+\infty))
wobei man den Energienullpunkt evtl. noch verschieben muss.
Ein Beispiel wäre das Wasserstoffatom mit
 = \left\{E_n \sim -n^{-2} \right\})
Die allgemeine Wellenfunktionen konstruiert man mittels
 = \sum_{E \in \sigma_p} \psi_E \, u_E(x) \, e^{-iEt} + \int_{\sigma_c} dE \, \psi(E) \, u_E(x) \, e^{-iEt} )
Üblicherweise würde man natürlich über Impulse summieren bzw. integrieren, d.h. man muss noch Entartungen sowie Normierungsfaktoren und Variablensubstitution berücksichtigen.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago.
Zuletzt bearbeitet von TomS am 14. Jan 2022 06:45, insgesamt 2-mal bearbeitet |
|
 |
Markooooo7
Anmeldungsdatum: 20.07.2021
Beiträge: 35
|
 Markooooo7 Verfasst am: 13. Jan 2022 18:15 Titel: Markooooo7 Verfasst am: 13. Jan 2022 18:15 Titel: |
 |
|
Hallo TomS,
vielen Dank für deine Antwort!
Was ich mich frage ist, was man macht, wenn man zwar für eine Energie, welche aus klassischer Sichtweise zu einer gebundenen Bewegung führt und damit dem diskreten Energiespektrum zugeordnet wird und man daraus für den speziellen Bereich, in dem die gebundene Bewegung abläuft eine Wellenfunktion berechnet, was ist dann mit den äußeren Bereichen, die bspw. klassisch verboten sind:
Würde man dann erst die Wellenfunktion aus dem gebundenen Bereich mit der Wellenfunktion im klassisch verbotenen Bereich verbinden und dann genau diese Wellenfunktion wie in deiner letzten Gleichung hingeschrieben, für die Lösung der Allgemeinen Schrödingergleichung benutzen und aufaddieren?
Vielen Dank im Voraus!
Mit freundlichen Grüßen
Marko |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 13. Jan 2022 18:26 Titel: TomS Verfasst am: 13. Jan 2022 18:26 Titel: |
 |
|
Jetzt geht was durcheinander.
Betrachte wieder das Wasserstoffatom. Sowohl gebundene Zustände E < 0 als auch ungebundene Zustände E > 0 haben Wellenfunktionen, die auf der gesamten reellen Zahlengerade definiert sind. D.h. die Aufenthaltswahrscheinlichkeit eines gebundenen Elektrons ist für beliebig große Abstände ungleich Null.
Um jeden möglichen Zustand eines Elektrons zu beschreiben, ist eben diese Darstellung notwendig.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Markooooo7
Anmeldungsdatum: 20.07.2021
Beiträge: 35
|
 Markooooo7 Verfasst am: 13. Jan 2022 19:51 Titel: Markooooo7 Verfasst am: 13. Jan 2022 19:51 Titel: |
 |
|
Hallo TomS,
was ich meine ist, was ist, wenn die Energie die ich betrachte in dem einen Intervall aufgrund des Potentials dem diskreten Spektrum zugeordnet wird, und in dem anderen Intervall der x-Achse dem kontinuierlichen Spektrum?
Wie konstruiere ich dann die allgemeine Wellenfunktion ähnlich deiner letzten Zeile deines ersten Beitrags?
Vielen Dank im Voraus!
Mit freundlichen Grüßen
Marko Pospiech |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 13. Jan 2022 22:47 Titel: TomS Verfasst am: 13. Jan 2022 22:47 Titel: |
 |
|
Also du meinst z.B.
 = - \frac{\alpha}{r})
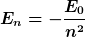
und zwei Bereiche
; \qquad r > r_n: \; E_n < V(r))
Eine zu einem n gehörige Eigenfunktionen gilt für den gesamten Definitionsbereich, also für die beiden genannten Bereiche. An der Stelle
)
passiert nichts außergewöhnliches (außer, wenn V(r) irgendwo unstetig ist und du die Schrödingergleichung je Bereich separat lösen musst; das ist aber in der Praxis nur in den einfachen Übungsbeispielen der Fall ;-)
Beispiel für die Relevanz: Stell dir vor, du hast ein Elektron in einem gebundenen Zustand mit festem E_n. Nun schaltest du eine zeitabhängige Störung h(t) im Hamiltonoperator ein, z.B. einen zeitabhängiges elektromagnetisches Feld. Dadurch wird die Wellenfunktion in einen neuen Zustand streuen, d.h. du erhältst den Übergang
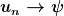
wobei zu psi i.A. alle Eigenfunktionen beitragen.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Markooooo7
Anmeldungsdatum: 20.07.2021
Beiträge: 35
|
 Markooooo7 Verfasst am: 14. Jan 2022 07:22 Titel: Markooooo7 Verfasst am: 14. Jan 2022 07:22 Titel: |
 |
|
Hallo TomS,
vielen Dank für deine Antwort!
Nein, ich meinte vielmehr ein Potential, stellen wir uns am besten eins vor, welches keine Radialsymmetrie hat, welches über den x-Bereich schwankt, also in Richtung x->>unendlich und x->>minus unendlich mehrere Minima hat.
Kann es dann vorkommen, dass es hier für eine GLEICHE Energie E, 2 Intervalle auf der x Achse gibt, wobei die Energie im ersten Intervall dem diskreten Spektrum und im zweiten Intervall dem kontinuierlichen Spektrum zugeordnet wird?
Vielen Dank im Voraus!
Mit freundlichen Grüßen
Marko |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 14. Jan 2022 09:06 Titel: TomS Verfasst am: 14. Jan 2022 09:06 Titel: |
 |
|
Nein.
1)
Siehe bitte nochmal das Beispiel des Wasserstoffatoms; ich habe genau diese Frage beantwortet ;-)
Jede einzelne Eigenfunktion der Schrödingergleichung ist eine Eigenfunktion auf dem gesamten dreidimensionalen Raum (in einfacheren Fälle auf der gesamten reellen Zahlengerade). Es ist sinnlos, den dreidimensionalen Raum oder die Zahlengerade in einzelne Bereiche zu unterteilen und dem Eigenwert hier oder dort unterschiedliche Eigenschaften zuzuschreiben. Wenn du diese Unterteilung doch vornimmst, weil das Potential stückweise stetig ist und du die Schrödingergleichung je Bereich separat löst, dann fügst du die Teile letztlich doch wieder zu einer Eigenfunktion zusammen.
Im Falle des Wasserstoffatoms habe ich je E_n die beiden Bereiche oben genannten; niemand würde aber auf die Idee kommen, die Eigenschaften des Spektrums separat zu betrachten
Man spricht manchmal von klassisch erlaubten und klassisch verbotenen Bereichen; im klassisch erlaubten Bereich findet man eine lokalisierte Wellenfunktion; diese Wellenfunktion wird im klassisch verbotenen Bereich klein sein und zum Beispiel exponentiell abfallen; trotzdem ist es eine Wellenfunktion, die als Ganzes - bzw. deren zugehöriger Eigenwert - entweder zum Punkt- oder zum kontinuierlichen Spektrum führt. Im Falle des Wasserstoffatoms ist für die Eigenfunktionen mit Eigenwert < 0 der gesamte rechte Bereich klassisch verboten. Das hat jedoch nichts mit der Frage der Spektren zu tun.
2)
Mathematisch kann man dies alles auf die Eigenschaften des Spektrums selbstadjungierter Operatoren zurückführen. Dabei betrachtet man die Eigenschaften der Operatorschar
^{-1})
für eine komplexe Zahl z. Insbs. geht es darum, ob diese sogenannte Resolvente R für ein bestimmtes z auf dem gesamten Hilbertraum definiert ist. Lax gesprochen besteht das Spektrum von H aus den Werten von z, für die dies nicht der Fall ist.
Wenn R definiert ist, dann gilt trivialerweise für eine Funktion f
 ^{-1} \, (H - z \text{id}) \, f = f )
Wenn R nicht definiert ist, weil
 \, f = 0)
d.h. wenn eine Eigenfunktion f zum Operator H mit Eigenwert z vorliegt, dann wird
 ^{-1} \, (H - z \text{id}) \, f = (H - z \text{id}) ^{-1} \, 0 = f )
offensichtlich sinnlos.
Wenn man nun das Spektrum genauer untersucht, so stellt man fest, dass es in drei Mengen zerfällt; in der Physik benötigt man meist nur zwei, nämlich das Punktspektrum und das diskrete Spektrum. Deren Eigenschaften folgen aus H als Ganzem, dazu muss in H noch nicht mal ein Potentialterm vorhanden sein.
In der Praxis sind die drei Teile des Spektrums disjunkt (ich weiß nicht, ob dies mathematisch beweisbar allgemein so ist). D.h. wenn man einen Eigenwert E hat, zu dem mehrere Eigenfunktionen gehören können (Entartung), dann sind alle Eigenfunktion entweder sämtlich normierbar - E gehört zum diskreten Spektrum, in einer genügend kleinen Umgebung zu E liegen keine weiteren Eigenwerte - oder nicht - E gehört zum kontinuierlichen Spektrum. Dies ist die wesentliche (physikalisch laxe) Unterscheidung zwischen den beiden Spektren. Wie du siehst, erfolgt dabei keine Betrachtung getrennter Bereiche der Koordinaten.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 14. Jan 2022 10:34 Titel: index_razor Verfasst am: 14. Jan 2022 10:34 Titel: |
 |
|
| TomS hat Folgendes geschrieben: |
Wenn man nun das Spektrum genauer untersucht, so stellt man fest, dass es in drei Mengen zerfällt; in der Physik benötigt man meist nur zwei, nämlich das Punktspektrum und das diskrete Spektrum.
|
Du meinst sicher das Punktspektrum und das kontinuierliche Spektrum.
| Zitat: |
In der Praxis sind die drei Teile des Spektrums disjunkt (ich weiß nicht, ob dies mathematisch beweisbar allgemein so ist).
|
Oft wird das kontinuierliche Spektrum so definiert, daß es disjunkt zum Punkt- und zum Restspektrum ist. (Dann gilt natürlich auch u = 0) nur für nur für 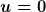 falls falls ) .) Zu Beweisen gibt es dann natürlich nichts. Manchmal definiert man das kontinuierliche Spektrum von H als das Spektrum der Einschränkung von H auf den Teilraum des Hilbertraums, dessen Elemente stetige Spektralmaße haben. Dann kann das kontinuierliche Spektrum auch Eigenwerte enthalten, beide Teilspektren sind dann also nicht disjunkt. (Normierbar sind die zugehörigen Eigenfunktionen natürlich in jedem Fall.) .) Zu Beweisen gibt es dann natürlich nichts. Manchmal definiert man das kontinuierliche Spektrum von H als das Spektrum der Einschränkung von H auf den Teilraum des Hilbertraums, dessen Elemente stetige Spektralmaße haben. Dann kann das kontinuierliche Spektrum auch Eigenwerte enthalten, beide Teilspektren sind dann also nicht disjunkt. (Normierbar sind die zugehörigen Eigenfunktionen natürlich in jedem Fall.) |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 14. Jan 2022 10:39 Titel: TomS Verfasst am: 14. Jan 2022 10:39 Titel: |
 |
|
Vorschlag für ein konkretes Beispiel:
Betrachte das Potential
 = \left\{ \begin{matrix} 0 & x < -b \\ V_0 & -b \le x \le -a \\ 0 & -a < x < +a \\ V_0 & +a \le x \le +b \\ 0 & x > +b \end{matrix} \right. )
mit zwei Potentialwällen 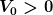 der Breite der Breite 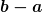 zwischen denen ein endlicher Potentialtopf eingeschlossen ist. zwischen denen ein endlicher Potentialtopf eingeschlossen ist.
1) Für Energien  folgen die Lösungen als ebene Wellen folgen die Lösungen als ebene Wellen
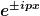
wobei der Zusammenhang zwischen p und E abschnittsweise durch
 )
])
gegeben ist.
Wie üblich muss also für eine Lösung geeignet aneinander gestückelt werden. Ich führe das jetzt nicht im Detail vor, aber die Strategie lautet wie folgt:
Für  = 0) gilt gilt

 = e^{\pm ipx})
Für  = V_0) gilt gilt
 = 2m[E - V_0] = p^2 - 2mV_0)
 = e^{\pm iqx})
Eine Eigenfunktion ) wird also durch diese zwei unterschiedlichen Exponentialfunktionen ausgedrückt. Es handelt sich aber nicht um zwei unterschiedliche Energie-Eigenfunktionen, je Bereich eine, einmal mit Eigenwert p und einmal mit q, sondern um ein und die selbe Eigenfunktion, in beiden Bereichen mit dem selben Energie-Eigenwert E. wird also durch diese zwei unterschiedlichen Exponentialfunktionen ausgedrückt. Es handelt sich aber nicht um zwei unterschiedliche Energie-Eigenfunktionen, je Bereich eine, einmal mit Eigenwert p und einmal mit q, sondern um ein und die selbe Eigenfunktion, in beiden Bereichen mit dem selben Energie-Eigenwert E.
2) Das selbe Verfahren funktioniert auch für Energien  , wobei jetzt innerhalb der Potentialwälle der obige Ansatz zu exponentieller Dämpfung führt. , wobei jetzt innerhalb der Potentialwälle der obige Ansatz zu exponentieller Dämpfung führt.
Soweit sollte das bekannt sein.
Nur zur Frage, zu welchem Spektrum eine Energie E als Eigenwert zum Hamiltonoperator H gehört: Die erlaubten Energien folgen bei derartigen Problemen üblicherweise aus den Anschlussbedingungen an den Sprungstellen des Potentials.
Wenn die erlaubten Eigenwerte E dann kontinuierlich sind, dann gehören sie zum kontinuierlichen Spektrum, andernfalls zum disktreten Spektrum. Das ist keine Aussage, die sich irgendwie auf einzelne Bereiche des Potentials bezieht.
Hinweis: die Lösung ist einfach aber algebraisch etwas aufwändig, da man die Anschlussbedingungen aufstellen und lösen muss. Außerdem sollte man die Symmetrie des Potentials beachten und statt der e-Funktionen besser Cosinus und Sinus verwenden, da dies zu Eigenfunktionen des Paritätsoperators führt.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Markooooo7
Anmeldungsdatum: 20.07.2021
Beiträge: 35
|
 Markooooo7 Verfasst am: 14. Jan 2022 18:32 Titel: Markooooo7 Verfasst am: 14. Jan 2022 18:32 Titel: |
 |
|
Ah, sehr gut, das hast du mir jetzt gut deutlich gemacht!
Vielen Dank! |
|
 |
|
|















