| Autor |
Nachricht |
DerNichtPhyisker
Anmeldungsdatum: 25.04.2021
Beiträge: 13
|
 DerNichtPhyisker Verfasst am: 09. Mai 2021 17:24 Titel: Elektrisches Feld und Potenzial DerNichtPhyisker Verfasst am: 09. Mai 2021 17:24 Titel: Elektrisches Feld und Potenzial |
 |
|
Hallo,
Ich habe eine Aufgabe bei der ich Probleme habe. Sie lautet:
"Betrachtet werden zwei [...] homogene geladene Kugelschalen mit Radius R_1 und R_2. Die innere Kugelschale mit R_1 hat eine Gesamtladung von +Q, die andere -Q."
Berechne Sie das Elektrische Feld für r < R_1 , R_1 < r < R_2 und r > R_2
und das elektrische Potenzial ("Unendliches Potenzial sei auf 0").
Folgende Lösung habe ich berechnet:
r < R_1:
E(r) = (+Q)/(2pi*epsilon_0) * 1/(R_1²)
Potenzial: Phi(r) = (+Q)/(2pi*epsilon_0) * 1/R_1
R_1 < r < R_2
E(r) = (-Q)/(2pi*epsilon_0) * 1/(R_2-R_1)²
Phi(r) = (-Q)/(2pi*epsilon_0) * ln(r_2-r_1)
r>R_2
E(r) = (+Q-Q^(-))/(2pi*epsilon_0) * 1/r²
Phi(r) = (+Q-Q^(-))/(2pi*epsilon_0) * 1/r
Meine Frage : Stimmen meine Ergebnisse?
Danke! |
|
 |
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5866
|
 Myon Verfasst am: 09. Mai 2021 17:36 Titel: Myon Verfasst am: 09. Mai 2021 17:36 Titel: |
 |
|
Nein, die Ergebnisse sind nicht richtig. Gut, das E-Feld für r>R2 ist gleich null, das stimmt.
Wie bist Du denn vorgegangen? Das E-Feld erhältst Du jeweils mit dem Gaussschen Gesetz, das Potential durch Integration des E-Felds. Das Potential ist nur bis auf eine Konstante bestimmt. Oft wird diese so gewählt, dass das Potential im Unendlichen verschwindet (ich sehe gerade, dass das sogar im Aufgabentext vorgegeben ist). |
|
 |
DerNichtPhyisker
Anmeldungsdatum: 25.04.2021
Beiträge: 13
|
 DerNichtPhyisker Verfasst am: 09. Mai 2021 17:44 Titel: DerNichtPhyisker Verfasst am: 09. Mai 2021 17:44 Titel: |
 |
|
Ich habe das Gauß-Gesetz aufgestellt, wobei ich das elektrische Feld als konstant angenommen habe. Das Flächenelement war einfach die halbe Kugeloberfläche, also 2pi*r².
Für das Potenzial habe ich Phi(r)= integral (E*ds) mit a = r und b = inf. |
|
 |
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5866
|
 Myon Verfasst am: 09. Mai 2021 17:58 Titel: Myon Verfasst am: 09. Mai 2021 17:58 Titel: |
 |
|
Die Annahme, dass das E-Feld konstant sei, ist nicht zulässig. Aus der Kugelsymmetrie der Anordnung und da das E-Feld konservativ ist folgt aber, dass das E-Feld nur von r abhängt und in radialer Richtung zeigt, d.h.
=E(r)\hat{e}_r)
Es genügt dann, nur E(r) zu bestimmen.
Um die Kugelsymmetrie auszunutzen, das Gausssche Gesetz immer auf Kugelschalen (natürlich mit gleichem Mittelpunkt wie die geladenen Schalen) anwenden. Es gilt dann
}\vec{E}(r)\cdot \dd \vec{\sigma}=4\pi r^2 E(r)=\frac{Q(r)}{\varepsilon_0})
wenn ) die Kugeloberfläche mit Radius r und Q(r) die darin eingeschlossene Ladung ist. die Kugeloberfläche mit Radius r und Q(r) die darin eingeschlossene Ladung ist. |
|
 |
DerNichtPhyisker
Anmeldungsdatum: 25.04.2021
Beiträge: 13
|
 DerNichtPhyisker Verfasst am: 09. Mai 2021 18:03 Titel: DerNichtPhyisker Verfasst am: 09. Mai 2021 18:03 Titel: |
 |
|
|
Warum ist das Flächenelement die komplette Oberfläche ? Ich dachte es wäre nur die halbe Oberfläche, weil es nur eine Kugelschale ist. |
|
 |
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5866
|
 Myon Verfasst am: 09. Mai 2021 22:34 Titel: Myon Verfasst am: 09. Mai 2021 22:34 Titel: |
 |
|
|
Mit Kugelschale ist die Oberfläche einer ganzen Kugel gemeint. |
|
 |
DerNichtPhyisker
Anmeldungsdatum: 25.04.2021
Beiträge: 13
|
 DerNichtPhyisker Verfasst am: 09. Mai 2021 22:44 Titel: DerNichtPhyisker Verfasst am: 09. Mai 2021 22:44 Titel: |
 |
|
|
Okay, danke. Was bedeutet eigentlich R_2 < r < R_1? Ich dachte ich müsste das Elektrische Feld der äußeren Kugelschale berechnen, weswegen ich deshalb R_2-R_1 gerechnet hatte. |
|
 |
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5866
|
 Myon Verfasst am: 09. Mai 2021 23:08 Titel: Myon Verfasst am: 09. Mai 2021 23:08 Titel: |
 |
|
Die Anordnung besteht ja aus 2 geladenen Kugelschalen mit Radius R1 und R2.
Das E-Feld soll angegeben werden für die 3 Bereiche
-das Innere der inneren Kugelschale, also für r<R1
-den Raum zwischen den beiden Kugelschalen, also für r zwischen R1 und R2 oder R1<r<R2
-den Raum ausserhalb der äusseren Kugelschale, also für r>R2. |
|
 |
DerNichtPhyisker
Anmeldungsdatum: 25.04.2021
Beiträge: 13
|
 DerNichtPhyisker Verfasst am: 09. Mai 2021 23:23 Titel: DerNichtPhyisker Verfasst am: 09. Mai 2021 23:23 Titel: |
 |
|
|
Warum war dann R_2-R_1 falsch? Ich verstehe nicht welchen Radius ich verwenden soll. Das Problem mit dem Flächenelement hat sich geklärt. Ich sehe auch grade, dass in meiner Aufgabe als Titel "Kugelkondensator" stand. Vielleicht hätte ich den Titel lesen sollen, dann wäre das Flächenelement richtig gewesen. |
|
 |
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5866
|
 Myon Verfasst am: 09. Mai 2021 23:32 Titel: Myon Verfasst am: 09. Mai 2021 23:32 Titel: |
 |
|
Das E-Feld zwischen den beiden Kugelschalen ist nicht konstant, sondern nimmt mit zunehmdem r ab.
Nach dem Gaussschen Gesetz gilt für ein r mit 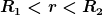 : :
=\frac{Q(r)}{\varepsilon_0}=\frac{Q}{\varepsilon_0})
Die letzte Gleichung gilt, da ja für eine Kugelschale zwischen R1 und R2 die eingeschlossene Ladung immer gleich +Q ist, die Ladung der inneren Kugelschale.
Die obige Gleichung einfach noch nach E(r) auflösen, dann ist das die Lösung für den 2. Bereich. |
|
 |
DerNichtPhyisker
Anmeldungsdatum: 25.04.2021
Beiträge: 13
|
 DerNichtPhyisker Verfasst am: 09. Mai 2021 23:40 Titel: DerNichtPhyisker Verfasst am: 09. Mai 2021 23:40 Titel: |
 |
|
|
Ich werde daraus nicht schlau. Dann unterscheiden sich die Bereiche nur über die Vorzeichen. Das heißt, dass es für r > R_2 gleich aussehen wird, nur dass ich die Ladung (+Q-Q^(-)) nehmen muss. Richtig? |
|
 |
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5866
|
 Myon Verfasst am: 10. Mai 2021 00:10 Titel: Myon Verfasst am: 10. Mai 2021 00:10 Titel: |
 |
|
Nur kurz: im 2. Bereich, zwischen den beiden Kugelschalen, gilt also
=\frac{Q}{4\pi\varepsilon_0 r^2},\quad R_1<r<R_2)
Für r<R1 und r>R2 ist die eingeschlossene Gesamtladung dagegen jeweils gleich null, deshalb gilt in diesen Bereichen nach dem Gaussschen Gesetz auch E(r)=0. |
|
 |
|















