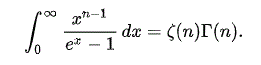| Autor |
Nachricht |
frage1
Anmeldungsdatum: 20.02.2021
Beiträge: 569
Wohnort: bayern
|
 frage1 Verfasst am: 10. März 2021 20:57 Titel: Energiedichte/Photonen frage1 Verfasst am: 10. März 2021 20:57 Titel: Energiedichte/Photonen |
 |
|
Meine Frage:
Hallo alle zusammen! Ich stecke wieder bei einer Aufgabe fest.
Die kosmische Hintergrundstrahlung des Universums ist äquivalent zu einem
Hohlraumstrahler bei einer Temperatur T = 2.7 K. Berechne
a) die Energiedichte des kosmischen Hintergrundes
b) die Anzahl der Photonen die diese in einem Würfel der Kantenlänge a = 1 cm beiträgt
Meine Ideen:
Meine Überlegung dazu wäre, dass man bei a) das plancksche Strahlungsgesetz anwendet und bei b) die Formel für die Leistung P= dE/dt bzw dN/dt= P/E. Aber was soll hier dises a=1? Wie soll ich damit rechnen? Müsste man hier nicht eine andere Formel verwenden? Aber ich kenne keine andere Formel, die diese situation beschreibt. Ich hoffe ihr könnt mir weiterhelfen. Danke schon mal im Voraus!
|
|
 |
Nils Hoppenstedt

Anmeldungsdatum: 08.01.2020
Beiträge: 2019
|
 Nils Hoppenstedt Verfasst am: 10. März 2021 21:59 Titel: Nils Hoppenstedt Verfasst am: 10. März 2021 21:59 Titel: |
 |
|
Hallo,
a) richtig
b) du teilst die spektrale Energiedichte u(f) durch die Energie eines Photons h*f und erhältst damit die spektrale Photonenzahldichte n(f). Integration über alle Frequenzen ergibt dann die Photonenzahldichte und anschließende Multiplikation mit dem Volumen schließlich die Photonenzahl.
Viele Grüße,
Nils
|
|
 |
frage1
Anmeldungsdatum: 20.02.2021
Beiträge: 569
Wohnort: bayern
|
 frage1 Verfasst am: 10. März 2021 23:46 Titel: frage1 Verfasst am: 10. März 2021 23:46 Titel: |
 |
|
|
Erstmals danke für deine Antwort. Aber wie soll ich das händisch integrieren, wenn man hier eine e funktion hat? Das plancksche szrahlungsgesetz beinhaltet ja eine e funktion und das Integral bilden ist ja sehr umfangreich. Oder denk ich da jetzt total falsch?
|
|
 |
Nils Hoppenstedt

Anmeldungsdatum: 08.01.2020
Beiträge: 2019
|
|
 |
frage1
Anmeldungsdatum: 20.02.2021
Beiträge: 569
Wohnort: bayern
|
 frage1 Verfasst am: 11. März 2021 14:43 Titel: frage1 Verfasst am: 11. März 2021 14:43 Titel: |
 |
|
|
Danke, nur das Problem ist, dass wir keinen Rechner verwenden dürfen, aber wir müssen trotzdem solche Aufgaben händisch rechnen können. Gibt´s da vielleicht eine andere Variante wie mans lösen kann? Wir haben in der VO auch nicht genau besprochen wie man solche formel integriert, nur kurz angeschnitten haben wir´s.
|
|
 |
frage1
Anmeldungsdatum: 20.02.2021
Beiträge: 569
Wohnort: bayern
|
 frage1 Verfasst am: 11. März 2021 14:45 Titel: frage1 Verfasst am: 11. März 2021 14:45 Titel: |
 |
|
|
Ich hab den Link erst jetzt gesehen. Ich schau mir das in Ruhe an und melde mich dann.
|
|
 |
Nils Hoppenstedt

Anmeldungsdatum: 08.01.2020
Beiträge: 2019
|
 Nils Hoppenstedt Verfasst am: 11. März 2021 15:37 Titel: Nils Hoppenstedt Verfasst am: 11. März 2021 15:37 Titel: |
 |
|
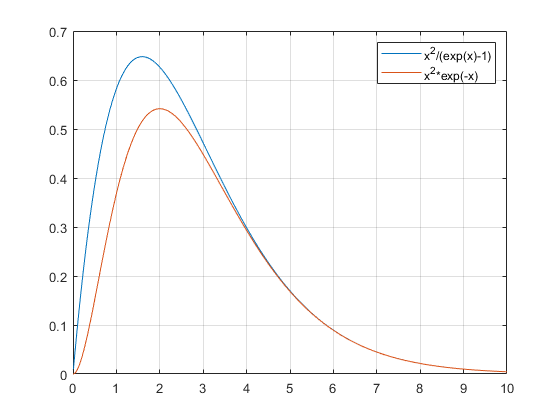
Wahrscheinlich erhält man auch eine ganz brauchbare Näherung für die Zahl der Photonen, wenn man einfach die Gesamtenergie in dem Volumen durch h*f_max teilt, wobei f_max die Frequenz ist, bei der die spektrale Energiedichte ihr Maximum besitzt.
Viele Grüße,
Nils
|
|
 |
frage1
Anmeldungsdatum: 20.02.2021
Beiträge: 569
Wohnort: bayern
|
 frage1 Verfasst am: 11. März 2021 16:01 Titel: frage1 Verfasst am: 11. März 2021 16:01 Titel: |
 |
|
|
Ich hab mir die Integration angeschaut und konnte es noch nicht ganz nachvollziehen. Könntest du mir vielleicht noch genauer erklären, wie ich das am besten lösen kann? danke!
|
|
 |
Nils Hoppenstedt

Anmeldungsdatum: 08.01.2020
Beiträge: 2019
|
 Nils Hoppenstedt Verfasst am: 11. März 2021 16:34 Titel: Nils Hoppenstedt Verfasst am: 11. März 2021 16:34 Titel: |
 |
|
Ich denke nicht, dass du in diesem Fall das Integral komplett selbst lösen musst. Es reicht bestimmt, wenn du das Integral so umschreibst, dass sie durch geeignete Substitution die obige Gestalt für n = 3 annimmt, sodass du einfach die Formel verwenden kannst. Das Integral ergibt dann Gamma(3)*Zeta(3) =~ 4.2.
Viele Grüße,
Nils
P.S.: die oben angesprochene Näherung funktioniert leider nicht so gut. Wenn ich mich nicht verrechnet habe, ist die so ermittelte Photonenzahl dann um einen Faktor 18 zu klein. Hier muss wohl doch exakt rechnen.
|
|
 |
frage1
Anmeldungsdatum: 20.02.2021
Beiträge: 569
Wohnort: bayern
|
 frage1 Verfasst am: 11. März 2021 20:43 Titel: frage1 Verfasst am: 11. März 2021 20:43 Titel: |
 |
|
|
Aber was soll ich mit a=1?
|
|
 |
Nils Hoppenstedt

Anmeldungsdatum: 08.01.2020
Beiträge: 2019
|
 Nils Hoppenstedt Verfasst am: 11. März 2021 21:11 Titel: Nils Hoppenstedt Verfasst am: 11. März 2021 21:11 Titel: |
 |
|
|
Was oben bereits gesagt, führt das Integral zunächst ja nur auf die Photonenanzahldichte. Um auf die Photonenanzahl zu kommen, muss man also noch mit dem Volumen des Würfels V = a³ multiplizieren.
|
|
 |
frage1
Anmeldungsdatum: 20.02.2021
Beiträge: 569
Wohnort: bayern
|
 frage1 Verfasst am: 11. März 2021 22:20 Titel: frage1 Verfasst am: 11. März 2021 22:20 Titel: |
 |
|
|
Ich komme beim Integrieren einfach nicht weiter. Vielleicht muss ich mir das noch genauer anschauen.
|
|
 |
Nils Hoppenstedt

Anmeldungsdatum: 08.01.2020
Beiträge: 2019
|
 Nils Hoppenstedt Verfasst am: 11. März 2021 23:40 Titel: Nils Hoppenstedt Verfasst am: 11. März 2021 23:40 Titel: |
 |
|
Also nochmal Schritt für Schritt:
1. Nimm die Plancksche Strahlungsformel für die Spektrale Energiedichte u(f)
2. Die spektrale Photonenzahldichte ist dann n(f) = u(f)/(hf)
3. Integriere nun über alle Frequenzen um auf die ("normale") Photonenzahldichte N zu kommen.
4. Im auftretendem Integral nun folgende Substitution verwenden:
f = kT/h*x, df = kT/h*dx
5. Wenn alles geklappt hat, müsste - bis auf Vorfaktoren - das obige Integral für n = 3 da stehen. Der Wert des Integrals ist 2.4.
6. Für die Zahl der Photonen im Würfel mit der Kantenlänge a folgt schließlich Z = N*a³
Viele Grüße,
Nils
|
|
 |
frage1
Anmeldungsdatum: 20.02.2021
Beiträge: 569
Wohnort: bayern
|
 frage1 Verfasst am: 13. März 2021 12:59 Titel: frage1 Verfasst am: 13. März 2021 12:59 Titel: |
 |
|
Wenn ich integriere bekomme ich komplett was anderes raus.
Wäre 8𝜋^5(𝑘𝑇)^4/15hc^3 falsch? Also ich schreib mal meine Rechnung auf:
Plancksches Strahlungsgesetz: u(f)=8𝜋hf^3/c^3(e^x -1). Jetzt durch hf teilen--> 8𝜋f^2/c^3*e^x -1. Und wenn ich das integriere bekomme ich: 8𝜋f^3/3c^3*e^x -1.
|
|
 |
Nils Hoppenstedt

Anmeldungsdatum: 08.01.2020
Beiträge: 2019
|
 Nils Hoppenstedt Verfasst am: 13. März 2021 14:43 Titel: Nils Hoppenstedt Verfasst am: 13. März 2021 14:43 Titel: |
 |
|
| frage1 hat Folgendes geschrieben: | | Plancksches Strahlungsgesetz: u(f)=8𝜋hf^3/c^3(e^x -1). Jetzt durch hf teilen--> 8𝜋f^2/c^3*e^x -1. Und wenn ich das integriere bekomme ich: 8𝜋f^3/3c^3*e^x -1. |
Du musst natürlich f überall ersetzen, wo es auftaucht und nicht nur in der e-Funktion. Und dann über x integrieren.
- Nils
|
|
 |
frage1
Anmeldungsdatum: 20.02.2021
Beiträge: 569
Wohnort: bayern
|
 frage1 Verfasst am: 15. März 2021 16:39 Titel: frage1 Verfasst am: 15. März 2021 16:39 Titel: |
 |
|
|
Was meinst du genau mit ersetzen? Ich hab´ ja nur nach der frequenz abgeleitet.
|
|
 |
Nils Hoppenstedt

Anmeldungsdatum: 08.01.2020
Beiträge: 2019
|
 Nils Hoppenstedt Verfasst am: 15. März 2021 17:09 Titel: Nils Hoppenstedt Verfasst am: 15. März 2021 17:09 Titel: |
 |
|
Na, du hast ja wohl offensichtlich im Exponent der e-Funktion f durch kT/h*x ersetzt (sonst würde da ja nicht e^x stehen). Und die gleiche Ersetzung musst du natürlich an ALLEN Stellen machen, wo f vorkommt. Also auch im Zähler der Strahlungsformel.
Zur Erinnerung: wir wollen das Integral durch Substitution f -> x lösen. In dem zu integrierenden Ausdruck darf dann natürlich kein f mehr vorkommen.
|
|
 |
Nils Hoppenstedt

Anmeldungsdatum: 08.01.2020
Beiträge: 2019
|
 Nils Hoppenstedt Verfasst am: 16. März 2021 00:18 Titel: Nils Hoppenstedt Verfasst am: 16. März 2021 00:18 Titel: |
 |
|
Ich meinte folgendes:
Die spektrale Photonenzahldichte ist nach Planck:

Integrieren über alle Frequenzen ergibt die integrale Photonenzahldichte:
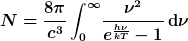
Nun wird substituiert:

 , ,
Man erhält:
^3\int_0^\infty \! \frac{x^2}{e^x-1} \, \dd x)
Mit Hilfe der obigen Formel aus dem Link ergibt dies:
^3\Gamma(3)\zeta(3)\approx 2.4\frac{8\pi}{c^3}\left(\frac{kT}{h}\right)^3)
Und die Zahl der Photonen in einem Würfel mit Kantenlänge a ist folglich:

Du musst jetzt nur noch die gegebenen Größen einsetzen.
Viele Grüße,
Nils
|
|
 |
frage1
Anmeldungsdatum: 20.02.2021
Beiträge: 569
Wohnort: bayern
|
 frage1 Verfasst am: 16. März 2021 23:28 Titel: frage1 Verfasst am: 16. März 2021 23:28 Titel: |
 |
|
Vielen lieben Dank! Ungelogen ich saß schon tagelang an dieser Rechnung. Ich wäre niemals auf die Idee gekommen, die Aufgabe so zu rechnen.. Bin echt dankbar für die ausführliche Erklärung.
Aber ich hätte noch paar Fragen: Muss ich das unbedingt integrieren? Denn man kann ja eine Näherung machen, so haben wir das zumindest immer in der VO gemacht. Und wie hätte man das Integral lösen können ohne jetzt den Link zu verwenden?
Ich schau mir die Rechnung morgen in Ruhe nochmal an und melde mich erneut falls Fragen auftauchen.
Und nochmal: vielen dank für die Hilfe!
|
|
 |
Nils Hoppenstedt

Anmeldungsdatum: 08.01.2020
Beiträge: 2019
|
|
 |
frage1
Anmeldungsdatum: 20.02.2021
Beiträge: 569
Wohnort: bayern
|
 frage1 Verfasst am: 18. März 2021 11:52 Titel: frage1 Verfasst am: 18. März 2021 11:52 Titel: |
 |
|
|
Perfekt, vielen vielen Dank! Bis jetzt hab ich alles verstanden. Falls etwas unklar sollte im Nachhinein, kann ich dir dann wieder Fragen stellen?
|
|
 |
frage1
Anmeldungsdatum: 20.02.2021
Beiträge: 569
Wohnort: bayern
|
 frage1 Verfasst am: 23. März 2021 19:04 Titel: frage1 Verfasst am: 23. März 2021 19:04 Titel: |
 |
|
Wie zu erahnen war, hab ich doch Fragen.
Ich habe den Rechenweg vom Prof. nicht ganz verstanden und kann die Rechnung irgendwie doch nicht ganz nachvollziehen.
|
|
 |
Nils Hoppenstedt

Anmeldungsdatum: 08.01.2020
Beiträge: 2019
|
 Nils Hoppenstedt Verfasst am: 23. März 2021 19:48 Titel: Nils Hoppenstedt Verfasst am: 23. März 2021 19:48 Titel: |
 |
|
|
Wo genau liegt das Problem?
|
|
 |
frage1
Anmeldungsdatum: 20.02.2021
Beiträge: 569
Wohnort: bayern
|
 frage1 Verfasst am: 24. März 2021 13:35 Titel: frage1 Verfasst am: 24. März 2021 13:35 Titel: |
 |
|
Wie ist man auf den Rechenweg gekommen?
| Beschreibung: |
|

Download |
| Dateiname: |
43DEE596-F8AF-4513-BD40-CB7EA2515648.jpeg |
| Dateigröße: |
73.95 KB |
| Heruntergeladen: |
144 mal |
|
|
 |
frage1
Anmeldungsdatum: 20.02.2021
Beiträge: 569
Wohnort: bayern
|
 frage1 Verfasst am: 24. März 2021 13:40 Titel: frage1 Verfasst am: 24. März 2021 13:40 Titel: |
 |
|
|
ich dachte, dass ich die Rechnung verstanden habe, aber anscheinend kann ichs immer noch nicht. Bin jetzt ziemlich verwirrt.
|
|
 |
frage1
Anmeldungsdatum: 20.02.2021
Beiträge: 569
Wohnort: bayern
|
 frage1 Verfasst am: 24. März 2021 13:49 Titel: frage1 Verfasst am: 24. März 2021 13:49 Titel: |
 |
|
bzw. :
| Beschreibung: |
|

Download |
| Dateiname: |
F2F3D547-3DA4-4F50-BFE1-AA5DFAD25185.jpeg |
| Dateigröße: |
96.32 KB |
| Heruntergeladen: |
392 mal |
|
|
 |
Nils Hoppenstedt

Anmeldungsdatum: 08.01.2020
Beiträge: 2019
|
 Nils Hoppenstedt Verfasst am: 24. März 2021 16:02 Titel: Nils Hoppenstedt Verfasst am: 24. März 2021 16:02 Titel: |
 |
|
Das ist jetzt war Aufgabenteil a (oben ging es ja in erster Linie um Aufgabenteil b), aber das Vorgehen ist immer gleich: Man kommt von der spektralen Dichte auf die "integrale" Dichte, in dem man über alle Frequenzen integriert. Im auftretenden Integral wird dann wie oben substituiert und dann das Integral gelöst. Entweder von Hand oder indem man die Lösung nachschlägt.
Viele Grüße,
Nils
|
|
 |
frage1
Anmeldungsdatum: 20.02.2021
Beiträge: 569
Wohnort: bayern
|
 frage1 Verfasst am: 24. März 2021 22:14 Titel: frage1 Verfasst am: 24. März 2021 22:14 Titel: |
 |
|
|
Naja, oke danke! Ich schau morgen nochmal drüber, hoffe, dass ichs dann verstehe.
|
|
 |
|