| Autor |
Nachricht |
Simon_7
Gast
|
 Simon_7 Verfasst am: 14. Aug 2020 21:23 Titel: SRT / Paradoxon (?) Simon_7 Verfasst am: 14. Aug 2020 21:23 Titel: SRT / Paradoxon (?) |
 |
|
Meine Frage:
Tag allerseits,
ich sitze seit geschlagenen 4 Tagen an folgendem, eigentlich recht einfachen Gedankenexperiment der SRT. Es ist eine Vereinfachung des Zwillingsparadoxons:
(Im Prinzip geht es um das Zwillingsparadoxon OHNE Rückflug)
Und zwar stellen wir uns zwei relativ zueinander bewegte Systeme A und B vor, sagen wir mit Geschwindigkeit  (so gewählt, dass der Lorentzfaktor (so gewählt, dass der Lorentzfaktor 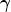 praktischerweise 2 gibt). praktischerweise 2 gibt).
Beide Systeme treffen sich / starten zum Zeitpunkt t (aus A) bzw t' (aus B) in x=x'=0.
Nun setzen wir uns in das Ruhesystem von A. Wir messen im Ruhesystem von A eine beliebige Länge in Bewegungsrichtung, (wie im Zwillingsparadoxon die Distanz zum nächsten Stern) und nennen diese  (z.B. 1000 000 000 meter). Aus Sicht von A sieh es so aus, dass B sich entlang (z.B. 1000 000 000 meter). Aus Sicht von A sieh es so aus, dass B sich entlang  bewegt und die Zeit dafür beträgt genau: bewegt und die Zeit dafür beträgt genau:

Aus der Sicht von A kommt B also nach 3.83 Sekunden beim "Ziel" in 1000 000 000 Meter Entfernung an.
Soweit so klar.
Die Länge  und die Zeit und die Zeit  erscheint im Ruhesystem des Beobachters in B verkürzt, gegeben durch die Zeitdilatation bzw Längenkontraktion: erscheint im Ruhesystem des Beobachters in B verkürzt, gegeben durch die Zeitdilatation bzw Längenkontraktion:

und

Mit  kommen wir darauf, dass B bis zum Ziel kommen wir darauf, dass B bis zum Ziel
 benötigt benötigt
und eine verkürzte Wegstrecke
 zurücklegt. zurücklegt.
Nun könnte man jedoch auch nach dem Relativitätsprinzip von System B als Ruhesystem ausgehen. Das führt dazu, dass  und und  als Ruhezeit bzw Ruhelänge betrachtet werden können. als Ruhezeit bzw Ruhelänge betrachtet werden können.
Jetzt kann man das Spiel umdrehen und System A als bewegend beobachten Demnach sagt Beobachter B, dass die Längen und Zeiten im Ruhesystem von A verkürzt werden zu:

und
 (gerundet) (gerundet)
Hier hört das bekannte Zwillingsparadoxon auf und sagt: Das widerspricht den realen Messungen von A. Das ist aber kein Problem solange sich A und B nicht treffen. Erst durch den Rückflug beschleunigt ein Beobachter und ist damit kein gleichwertiges Inertialsystem mehr (bzw hat es gewechselt), womit der Widerspruch aufgehoben ist.
Okay, aber was ist, wenn der Zwilling B NICHT umdreht? Dann bleibt dieses "Paradoxon" bestehen. Um die Antwort "Das ist kein Paradoxon solange sie nicht voneinander erfahren" vorwegzunehmen: Doch ist es, da:
Wir könnten uns nach dem Wechsel von A in B und zurück zu A (wie oben) ja einfach wieder in B setzen mit den zuletzt berechneten Werten  und und  . Dann hätte B selbst wieder die Hälfte der initialen Messwerte ( . Dann hätte B selbst wieder die Hälfte der initialen Messwerte (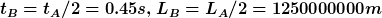 ). Das widerspricht den eigenen Messungen, die sich durch ein legitimes Wechseln der Bezugsysteme nicht verändern dürften. Allein schon, dass durch zweimaliges Wechseln der Perspektive (was physikalisch völlig erlaubt ist), die Längen und Zeiten nicht denselben entsprechen ist ein Paradoxon. ). Das widerspricht den eigenen Messungen, die sich durch ein legitimes Wechseln der Bezugsysteme nicht verändern dürften. Allein schon, dass durch zweimaliges Wechseln der Perspektive (was physikalisch völlig erlaubt ist), die Längen und Zeiten nicht denselben entsprechen ist ein Paradoxon.
Dazu kommt ein weiteres Paradoxon:
Man könnte nun wieder in A wechseln und so weiter... Das könnte man beliebig oft treiben und immer zwischen den zwei Inertialsystemen hin- und her wechseln, solange bis 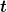 und und 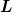 gegen Null gehen. Das macht keinen Sinn. gegen Null gehen. Das macht keinen Sinn.
Bei dieser Überlegung muss ein Logikfehler vorliegen. Ich suche ihn seit geraumer Zeit, komme aber leider nicht darauf.
Ich hoffe, dass mir ein paar SRT-Profis damit weiterhelfen können:)
Ich bedanke mich für eine Antwort!
LG Simon
Meine Ideen:
Alle "Ideen" sind im Problem integriert:)
Bzw: Das Problem "ist die Idee"  |
|
 |
DrStupid
Anmeldungsdatum: 07.10.2009
Beiträge: 5041
|
 DrStupid Verfasst am: 15. Aug 2020 15:22 Titel: DrStupid Verfasst am: 15. Aug 2020 15:22 Titel: |
 |
|
Da ich nicht wirklich nachvollziehen kann, was Du da beschreibst, habe ich es einfach mal selbst nachgerechnet. Angenommen, A und B starten im Ruhesystem von A bei X=(0,0). A bleibt am selben Ort und befindet sich nach der Zeit t bei Y=(t,0). B bewegt sich mit der Geschwindigkeit v und befindet sich nach der Zeit t bei Z=(t,v·t).
Jetzt transformiere ich das mittels

und

ins Ruhesystem von B und erhalte
)
)
)
Die Retransformation in das Ruhesystem von A (das sich gegenüber B mit -v bewegt) führt wieder zu
 = X)
 = Y)
 = Z)
Das von Dir vermutete Paradoxon kann ich nicht erkennen und da ich nicht wirklich verstehe, was Du genau tust (insbesondere beim Wechsel aus dem Ruhesystem von B zurück in das von A), kann ich auch nicht sagen, wo der Fehler liegt. Üblicherweise wird bei solchen Gedankenexperimenten die Relativität der Gleichzeitigkeit übersehen. In diesem Fall könnte das Problem darin liegen, dass die Ereignisse Y' und Z' nicht gleichzeitig stattfinden. |
|
 |
Simon98
Anmeldungsdatum: 07.08.2020
Beiträge: 8
|
 Simon98 Verfasst am: 15. Aug 2020 18:04 Titel: Simon98 Verfasst am: 15. Aug 2020 18:04 Titel: |
 |
|
Hi,
sorry, vielleicht beschreibe ich das Problem nochmal kürzer und kompakter:
Selbe Voraussetzungen wie eben, also System A und B bewegen sich relativ zueinander mit Geschwindigkeit v in x-Richtung, zum Zeitpunkt t=t'=0 sind beide Koordinatenursprünge am selben Ort. v sei wieder so gewählt, dass der Lorentzfaktor = 2 ist.
Nun platziere ich eine ruhende Uhr in A. Sagen wir bei ihr vergehen aus der Sicht vom Ruhesystem A genau 4 Sekunden (sie macht vier mal "tick").
Nun vergeht durch die Lorentztransformation in B genau 2 Sekunden, also eine Uhr, die in B ruht macht zwei mal "tick" . Das ist die Eigenzeit von B, also sind sich A und B in dem einig.
Wenn man nun aber B als Ruhesystem betrachtet, dann hat die Uhr zwei mal "tick" gemacht, aber A ist das bewegte System. Das bedeutet, dass nach der Lorentztransformation die Uhr in A nur 1 mal "tick" macht.
Wenn man dabei immer hin- und herwechselt und immer die Lorentztransformation benutzt, dann werden die Zeiten (analog für Längen) unendlich klein.
Ist das so besser ausgedrückt? Falls nicht kannst Du mir gerne sagen, wo ich mich nicht klar ausgedrückt habe!
LG |
|
 |
DrStupid
Anmeldungsdatum: 07.10.2009
Beiträge: 5041
|
 DrStupid Verfasst am: 15. Aug 2020 20:34 Titel: DrStupid Verfasst am: 15. Aug 2020 20:34 Titel: |
 |
|
| Simon98 hat Folgendes geschrieben: | Nun platziere ich eine ruhende Uhr in A. Sagen wir bei ihr vergehen aus der Sicht vom Ruhesystem A genau 4 Sekunden (sie macht vier mal "tick").
Nun vergeht durch die Lorentztransformation in B genau 2 Sekunden, also eine Uhr, die in B ruht macht zwei mal "tick" . Das ist die Eigenzeit von B, also sind sich A und B in dem einig. |
Bis hierhin kann ich Dir noch folgen. Offenbar vergleichst Du die Zeiten, die die Uhren von A und B am Endpunkt der Reise von B anzeigen.
| Simon98 hat Folgendes geschrieben: | | Wenn man nun aber B als Ruhesystem betrachtet, dann hat die Uhr zwei mal "tick" gemacht, aber A ist das bewegte System. Das bedeutet, dass nach der Lorentztransformation die Uhr in A nur 1 mal "tick" macht. |
Aber hier weiß ich nicht, was Du meinst. Von welchen Zeiten sprichst Du hier? Wenn die Sichtweise komplett umgekehrt werden soll, dann musst Du die Zeiten vergleichen, die die Uhren am Endpunkt der Reise von A anzeigen. Und da steht die Uhr von A bei 4 Sekunden und die von B bei 8 Sekunden. Das ist der gleiche Faktor wie bei B aus Sicht von A. |
|
 |
Simon98
Anmeldungsdatum: 07.08.2020
Beiträge: 8
|
 Simon98 Verfasst am: 16. Aug 2020 00:21 Titel: Simon98 Verfasst am: 16. Aug 2020 00:21 Titel: |
 |
|
Hi,
ja, genau - ich versuche die Sichtweise komplett umzukehren wie Du gesagt hast!
Das darf man ja nach dem Relativitätsprinzip.
Wieso sollte B dann 8 Sekunden haben? Eigentlich sollte die Uhr in B doch 2 Sekunden zeigen, oder nicht? Das wäre zumindest die Eigenzeit, die vorher berechnet wurde.
Genau dabei stoße ich auf das Problem!  Denn wenn es 2 Sekunden wären, dann konnte man wieder die Sichtweise komplett umkehren und hätte 1 Sekunde und so weiter.... Denn wenn es 2 Sekunden wären, dann konnte man wieder die Sichtweise komplett umkehren und hätte 1 Sekunde und so weiter....
Danke schon mal! |
|
 |
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5852
|
 Myon Verfasst am: 16. Aug 2020 08:20 Titel: Myon Verfasst am: 16. Aug 2020 08:20 Titel: |
 |
|
| Simon98 hat Folgendes geschrieben: | | Wenn man nun aber B als Ruhesystem betrachtet, dann hat die Uhr zwei mal "tick" gemacht, aber A ist das bewegte System. Das bedeutet, dass nach der Lorentztransformation die Uhr in A nur 1 mal "tick" macht. |
Aus meiner Sicht liegt der Irrtum darin, dass Du die Sichtweise nicht einfach „umkehren“ kannst. Die Strecke, die der Ursprung von B in System A zurücklegt, ruht im System A (Du kannst dir ja einen ruhenden Massstab in System A vorstellen).
Zwischen den beiden Ereignissen „Ursprung von System B passiert Anfang des Massstabs“ und „Ursprung von B passiert Ende des Massstabs“ messe ein Beobachter in A 4s, dann misst ein Beobachter in B hierfür 2s. Was kehrst Du nun genau um? |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18026
|
 TomS Verfasst am: 16. Aug 2020 08:29 Titel: TomS Verfasst am: 16. Aug 2020 08:29 Titel: |
 |
|
Jetzt habe ich dein Problem verstanden, du iterierst die Vorgehensweise.
Versuchen wir mal einen völlig anderen Zugang zum Zwillingsparadoxon. Betrachten wir zwei Reiserouten - zunächst mit gemeinsamen Start und Endpunkt - die ansonsten beliebig, also auch gekrümmt und beschleunigt verlaufen.
In diesem Fall kannst du deine wechselweise Betrachtung der Zwillinge (zunächst) nicht durchführen, da die Zeitdilatation eines beschleunigten Zwillings, betrachtet aus dem beschleunigten System des anderen Zwillings, extrem kompliziert zu berechnen ist. Deine Idee ist rein mathematisch nicht durchführbar, du benötigst andere Methoden.
Allerdings kann jeder einzelne Zwilling seine Uhr mitführen, beim Start mit dem Zwilling synchronisieren, unterwegs beliebig ablesen sowie am Ende direkt mit der des Bruders vergleichen. Er hat also immer noch seine objektive Eigenzeit.
Zur Berechnung der beiden Eigenzeiten (also jeweils der eigenen sowie der des Zwillings) können sich beide Zwillinge auf ein drittes, gedachtes Inertialsystem einigen, sie können unterschiedliche, sogar beliebige Inertialsysteme nutzen, wenn Ihre mathematischen Fähigkeiten ausreichen können sie tatsächlich auch ihr eigenes beschleunigtes Bezugsystem nutzen.
Betrachten wir Zwilling A mit Route C_A und die auf seiner Uhr gemessene Eigenzeit 
Nun betrachten wir diverse Berechnungen, z.B. in gedachten Inertialsystemen S, S‘ ... oder auch aus dem Bezugsystem von B, notiert mittels Indizes. Für die eindeutig gemessene sowie für sämtliche berechneten gilt Zeiten gilt

Für B analog.
Die auf der jeweils eigenen Uhr abgelesene Eigenzeit ist also eine objektive Größe, über die verschiedene Beobachter A, S, S‘, ... B und beliebige andere Beobachter objektive Einigkeit erzielen. Sie berechnen mittels unterschiedlicher Methoden einfach die eine eindeutige Zeit, die mit der tatsächlich auf der jeweiligen Uhr abgelesenen übereinstimmt - darüber muss ja Einigkeit bestehen.
Wir müssen nun nicht unbedingt Reisen mit gemeinsamen Endpunkten betrachten, dabei entfällt lediglich die Möglichkeit des direkten Uhrenvergleichs. Alternativ könnte ein Zwilling bei seiner Landung auf dem Mars ein Photo aufnehmen und seinem Bruder senden. Die o.g. Argumentation bleibt gültig, beide haben jeweils eine eindeutige Zeitanzeige auf ihrer eigenen Uhr, der eine im Moment der Landung, der andere im Moment des Empfangs des Photos. Und sie können beide die Zeitanzeige des jeweils anderen eindeutig berechnen.
Wenn du nun den objektiven und invarianten Charakter der Eigenzeit verstanden hast, sollte klar sein, dass die iterierte Betrachtung schlicht nicht zulässig ist.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Simon98
Anmeldungsdatum: 07.08.2020
Beiträge: 8
|
 Simon98 Verfasst am: 16. Aug 2020 12:55 Titel: Simon98 Verfasst am: 16. Aug 2020 12:55 Titel: |
 |
|
[quote="Myon"] | Simon98 hat Folgendes geschrieben: |
Zwischen den beiden Ereignissen „Ursprung von System B passiert Anfang des Massstabs“ und „Ursprung von B passiert Ende des Massstabs“ messe ein Beobachter in A 4s, dann misst ein Beobachter in B hierfür 2s. Was kehrst Du nun genau um? |
Die Sichtweise kehrt man um, also man nimmt System B als ruhend an, was ja nach dem Relativitätsprinzip möglich ist. |
|
 |
Simon98
Anmeldungsdatum: 07.08.2020
Beiträge: 8
|
 Simon98 Verfasst am: 16. Aug 2020 13:02 Titel: Simon98 Verfasst am: 16. Aug 2020 13:02 Titel: |
 |
|
| TomS hat Folgendes geschrieben: | Jetzt habe ich dein Problem verstanden, du iterierst die Vorgehensweise.
Wenn du nun den objektiven und invarianten Charakter der Eigenzeit verstanden hast, sollte klar sein, dass die iterierte Betrachtung schlicht nicht zulässig ist. |
@TomS:
Ich denke, Deine Antwort wahr sehr hilfreich!!
Habe ich den invarianten Charakter der Eigenzeit so richtig verstanden:
Aus der Sicht von A misst man die Eigenzeit z. B. 10 Jahre zum Mars (um bei Deinem Beispiel zu bleiben).
Man beobachtet andererseits, dass B 7 Jahre benötigt wegen der Zeitdilatation.
Beides sind die Eigenzeiten der jeweiligen Systeme.
Wenn man nun B als ruhend betrachtet, also das Ruhesystem wechselt, dann sieht man zwar Uhren in A langsamer ticken, jedoch bleibt die Eigenzeit von A, also 10 Jahre, invariant. Man kann diese aus B berechnen , aber nicht beobachten. Das bedeutet aber auch, dass wenn B so beschleunigen würde, dass es relativ zu A ruhen würde, dann würden sie sich auf die 10 Jahre einigen.
Was ich daran komisch finde ist, dass aus der Sicht des Ruhesystems B, A immer noch verlangsamt erscheinen muss.
Ich bedanke mich schon mal sehr bei allen, die mir gerade antworten  Das ist wirklich sehr nett! Das ist wirklich sehr nett!
Zuletzt bearbeitet von Simon98 am 16. Aug 2020 16:50, insgesamt einmal bearbeitet |
|
 |
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5852
|
 Myon Verfasst am: 16. Aug 2020 13:19 Titel: Myon Verfasst am: 16. Aug 2020 13:19 Titel: |
 |
|
| Simon98 hat Folgendes geschrieben: | | Die Sichtweise kehrt man um, also man nimmt System B als ruhend an, was ja nach dem Relativitätsprinzip möglich ist. |
Ein Körper kann in einem bestimmten System ruhen, das ist dann ein Ruhesystem des Körpers. Aber was meinst Du mit „man nimmt System B als ruhend an“? Das ergibt m.E. keinen Sinn. Ruhend bezüglich was? |
|
 |
Simon98
Anmeldungsdatum: 07.08.2020
Beiträge: 8
|
 Simon98 Verfasst am: 16. Aug 2020 16:53 Titel: Simon98 Verfasst am: 16. Aug 2020 16:53 Titel: |
 |
|
| Myon hat Folgendes geschrieben: | | Simon98 hat Folgendes geschrieben: | | Die Sichtweise kehrt man um, also man nimmt System B als ruhend an, was ja nach dem Relativitätsprinzip möglich ist. |
Ein Körper kann in einem bestimmten System ruhen, das ist dann ein Ruhesystem des Körpers. Aber was meinst Du mit „man nimmt System B als ruhend an“? Das ergibt m.E. keinen Sinn. Ruhend bezüglich was? |
Ruhend bezüglich uns als Beobachter. Man muss ja immer um eine Betrachtung in der SRT durchführen zu können, irgendein System als aktuelles Ruhesystem nehmen und aus der Sicht von diesem Ruhesystem dann die Beobachtungen und Messungen machen. |
|
 |
Container
Anmeldungsdatum: 16.08.2020
Beiträge: 2
|
 Container Verfasst am: 16. Aug 2020 17:12 Titel: Container Verfasst am: 16. Aug 2020 17:12 Titel: |
 |
|
| DrStupid hat Folgendes geschrieben: | Da ich nicht wirklich nachvollziehen kann, was Du da beschreibst, habe ich es einfach mal selbst nachgerechnet. Angenommen, A und B starten im Ruhesystem von A bei X=(0,0). A bleibt am selben Ort und befindet sich nach der Zeit t bei Y=(t,0). B bewegt sich mit der Geschwindigkeit v und befindet sich nach der Zeit t bei Z=(t,v·t).
Jetzt transformiere ich das mittels

und

ins Ruhesystem von B und erhalte
)
)
)
Die Retransformation in das Ruhesystem von A (das sich gegenüber B mit -v bewegt) führt wieder zu
 = X)
 = Y)
 = Z)
Das von Dir vermutete Paradoxon kann ich nicht erkennen und da ich nicht wirklich verstehe, was Du genau tust (insbesondere beim Wechsel aus dem Ruhesystem von B zurück in das von A), kann ich auch nicht sagen, wo der Fehler liegt. Üblicherweise wird bei solchen Gedankenexperimenten die Relativität der Gleichzeitigkeit übersehen. In diesem Fall könnte das Problem darin liegen, dass die Ereignisse Y' und Z' nicht gleichzeitig stattfinden. |
|
|
 |
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5852
|
 Myon Verfasst am: 16. Aug 2020 21:27 Titel: Myon Verfasst am: 16. Aug 2020 21:27 Titel: |
 |
|
| Simon98 hat Folgendes geschrieben: | | Ruhend bezüglich uns als Beobachter. Man muss ja immer um eine Betrachtung in der SRT durchführen zu können, irgendein System als aktuelles Ruhesystem nehmen und aus der Sicht von diesem Ruhesystem dann die Beobachtungen und Messungen machen. |
Natürlich kann man eine Situation immer von einem bestimmten System aus betrachten. Grundsätzlich aber sind alle Systeme gleichberechtigt, man wählt nicht ein „Ruhesystem“. Ein Ruhesystem bezieht sich immer auf einen Körper, eine Person etc., die in dem betreffenden System ruht.
Die beiden Ereignisse
-„Ursprung von System B fällt mit Ursprung von System A zusammen“
-„Ursprung von System B passiert Ende der in A ruhenden Strecke L“
können jeweils in Raumzeitkoordinaten bezüglich des Systems A oder Systems B angegeben werden, und die Koordinaten können durch Lorentztransformationen ineinander umgerechnet werden. Die Strecke L ruht aber in System A, und die Situation kann nicht einfach „umgekehrt“ werden. Es ist für ein Beobachter in System B, für welchen die Strecke verkürzt erscheint im Vergleich zur Ruhelänge L. |
|
 |
DrStupid
Anmeldungsdatum: 07.10.2009
Beiträge: 5041
|
 DrStupid Verfasst am: 23. Aug 2020 19:47 Titel: DrStupid Verfasst am: 23. Aug 2020 19:47 Titel: |
 |
|
| Simon98 hat Folgendes geschrieben: | | Wieso sollte B dann 8 Sekunden haben? |
Die Gleichungen für die Transformationen stehen oben. Rechne es nach.
| Simon98 hat Folgendes geschrieben: | | Eigentlich sollte die Uhr in B doch 2 Sekunden zeigen, oder nicht? |
Nicht nach meiner Rechnung.
| Simon98 hat Folgendes geschrieben: | | Das wäre zumindest die Eigenzeit, die vorher berechnet wurde. |
Auch auf die Gefahr hin, mich zu wiederholen: Welche Zeit ist das? Die Uhren zeigen alle möglichen Zeiten an - je nachdem, wann man sie abliest. Nach welchem Kriterien wählst Du den Zeitpunkt bzw. die Zeitspanne aus und was kommt mit denselben Kriterien im jeweils anderen Ruhesystem heraus? Ich habe die Zeiten ausgerechnet, bei denen ein Beobachter im Ruhesystem des jeweils anderen am Ziel ankommt. Von welchen Zeiten sprichst Du? |
|
 |
Simon98
Anmeldungsdatum: 07.08.2020
Beiträge: 8
|
 Simon98 Verfasst am: 24. Aug 2020 21:44 Titel: Simon98 Verfasst am: 24. Aug 2020 21:44 Titel: |
 |
|
Erst mal Danke an alle!
Ich habe inzwischen die Lösung für alle, die es interessiert:
Der Schlüssel ist, dass sich beide Beobachter grundsätzlich nicht einig sind, ob B angekommen ist oder nicht. Aus der Sicht von A kommt dieser nach einer Zeit t an, aus der Sicht von B bei t/2. B wird dann sehen, dass A's Uhr bei seiner Ankunft in der Tat t/4 misst, wird also darauf schließen, dass A sagt, dass B noch nicht angekommen ist. |
|
 |
DrStupid
Anmeldungsdatum: 07.10.2009
Beiträge: 5041
|
 DrStupid Verfasst am: 25. Aug 2020 01:03 Titel: DrStupid Verfasst am: 25. Aug 2020 01:03 Titel: |
 |
|
| Simon98 hat Folgendes geschrieben: | | Aus der Sicht von A kommt dieser nach einer Zeit t an, aus der Sicht von B bei t/2. |
Mir ist immer noch nicht klar, was Du meinst. Aus seiner eigenen Sicht bewegt sich Beobachter B doch gar nicht. Wie kann er da irgendwo ankommen? |
|
 |
VeryApe

Anmeldungsdatum: 10.02.2008
Beiträge: 3247
|
 VeryApe Verfasst am: 25. Aug 2020 08:43 Titel: VeryApe Verfasst am: 25. Aug 2020 08:43 Titel: |
 |
|
| Zitat: |
Nun platziere ich eine ruhende Uhr in A. Sagen wir bei ihr vergehen aus der Sicht vom Ruhesystem A genau 4 Sekunden (sie macht vier mal "tick").
Nun vergeht durch die Lorentztransformation in B genau 2 Sekunden, also eine Uhr, die in B ruht macht zwei mal "tick" . Das ist die Eigenzeit von B, also sind sich A und B in dem einig.
|
Für die von einem in A ruhenden Beobachter gemessene Länge braucht B nach der Zeit von A 4 ticks aber nach der mitgerführten Uhr von B 2 ticks
| Zitat: |
Wenn man nun aber B als Ruhesystem betrachtet, dann hat die Uhr zwei mal "tick" gemacht, aber A ist das bewegte System. Das bedeutet, dass nach der Lorentztransformation die Uhr in A nur 1 mal "tick" macht.
|
Ja die Uhr hat zweimal tick gemacht im Ruhsystem B und nach der Gleichzeitigkeit von B eruiert der dort anwesende das die Uhr von A nur 1 mal tick gemacht hat. Er kann aber nicht darausschließen nur aufgrund der Zeitdilatation das A nun urteilt er hätte nach seiner Zeit für die gesamte Strecke nur 1 tick gebraucht. Die Zeitdilatation alleine funktioniert nur wenn man immer dieselbe Uhr vergleicht. Dazu müsste man nun ein Lichtsignal von B nach A schicken, wenn B dort angelangt ist und wenn dieses Signal bei der zeitdilatierten A Uhr (aus sicht für B) ankommt, dann die Lichtlaufzeit nach A System abrechnen, oder man weiß das Uhren die für A ruhen und entlang der Strecke aufgestellt wären und sychron rennen, für B nicht nur zeitdilatiert rennen sondern ja nach Position vor und nachrechnen.
Am Start müsste man mit einer anderen Uhr vergleichen wie am Ende und diese Uhren rennen auch nun nicht synchron.
Wenn ich mich aber nur auf die Zeitdilatation begrenze, dann kommt mir das so vor.
A gibt an 4 tics is Gleichzeitig 2 tics von B
B gibt an 2 tics is gleichzeitig 1 tic von A
A gibt an 1 tic is gleichzeitig 0.5 tic von B
B gibt an 0.5 tic is gleichzeitig 0.25 tic von A usw.
das ist zwar alles richtig, aber für was gut?
Das erinnert mich doch an dieses Paradoxon https://www.lernhelfer.de/schuelerlexikon/mathematik-abitur/artikel/das-paradoxon-von-achilles-und-der-schildkroete
_________________
WAS IST LOS IN EUROPA? https://www.youtube.com/watch?v=a9mduhSSC5w |
|
 |
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5852
|
 Myon Verfasst am: 25. Aug 2020 12:21 Titel: Myon Verfasst am: 25. Aug 2020 12:21 Titel: |
 |
|
| Simon98 hat Folgendes geschrieben: | | B wird dann sehen, dass A's Uhr bei seiner Ankunft in der Tat t/4 misst, wird also darauf schließen, dass A sagt, dass B noch nicht angekommen ist. |
Ja, t/4 ist die Zeit(differenz), die B auf einer im System von A ruhenden Uhr abliest. Dies ist nicht die Zeit, die der Beobachter A für das Durchfahren der Strecke durch B misst.
Nochmals mit etwas anderen Worten als VeryApe: Um die Zeit zu messen, die B für die Strecke benötigt, kann A zwei in seinem System synchronisierte Uhren am Start- und Endpunkt der Strecke verwenden. Im System von B sind die Uhren nicht synchronisiert.
Wenn beim Start die Uhr am Startpunkt und die Uhr von B jeweils auf null gestellt sind, und A für das Zurücklegen der Strecke die Zeit t misst, so liest B am Ende der Strecke auf seiner Uhr die Zeit t/2 ab. Zum selben Zeitpunkt liest B bei der Uhr am Ende der Strecke die Zeit t ab, und für die Uhr beim Start misst er in seinem System den Stand t/4. Hoffe, das ist so richtig... |
|
 |
|
|

















 Denn wenn es 2 Sekunden wären, dann konnte man wieder die Sichtweise komplett umkehren und hätte 1 Sekunde und so weiter....
Denn wenn es 2 Sekunden wären, dann konnte man wieder die Sichtweise komplett umkehren und hätte 1 Sekunde und so weiter....