| Autor |
Nachricht |
positive
Anmeldungsdatum: 06.12.2013
Beiträge: 494
|
 positive Verfasst am: 21. Jan 2016 00:38 Titel: Der schiefe, positive Turm |
 |
|
[jh8979: Ich hab das folgende von dieser Diskussion hier abgespalten, da sie sich vom -durchaus interessanten- Thema arg weit entfernt hat:
http://www.physikerboard.de/ptopic,265235.html#265235 ]
Dem Artikel zufolge gibt es so gut wie keine exakten Lösungen, teilweise soll auch unklar sein, ob manche Lösungen richtig sind, etc, inwiefern soll sowas glaubwürdig dazu beitragen, dass irgendwann eine Theorie von Physikern aufgestellt wird, die die Welt erklären kann? Warum sollte das Ganze einem nicht eher als der Turm von Babel vorkommen?
|
|
 |
jh8979
Moderator
Anmeldungsdatum: 10.07.2012
Beiträge: 8575
|
| jh8979 Verfasst am: 21. Jan 2016 08:06 Titel: |
|
|
| positive hat Folgendes geschrieben: | | Dem Artikel zufolge gibt es so gut wie keine exakten Lösungen, teilweise soll auch unklar sein, ob manche Lösungen richtig sind, etc, inwiefern soll sowas glaubwürdig dazu beitragen, dass irgendwann eine Theorie von Physikern aufgestellt wird, die die Welt erklären kann? Warum sollte das Ganze einem nicht eher als der Turm von Babel vorkommen? |
Der Artikel ist wie gesagt unheimlich schlecht und z.T. falsch. Das ist also nur ein bedingt guter Ausgangspunkt als Diskussionsgrundlage für weiteres...
Zuletzt bearbeitet von jh8979 am 22. Jan 2016 10:15, insgesamt einmal bearbeitet |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18007
|
| TomS Verfasst am: 22. Jan 2016 07:48 Titel: |
|
|
| positive hat Folgendes geschrieben: | | Dem Artikel zufolge gibt es so gut wie keine exakten Lösungen, teilweise soll auch unklar sein, ob manche Lösungen richtig sind, etc, inwiefern soll sowas glaubwürdig dazu beitragen, dass irgendwann eine Theorie von Physikern aufgestellt wird, die die Welt erklären kann? Warum sollte das Ganze einem nicht eher als der Turm von Babel vorkommen? |
Ob die Lösung eines Problems mathematisch geschlossen formuliert werden kann, ist völlig irrelevant. Relevant und praktisch bedeutsam ist, dass eine Lösung prinzipiell existiert, eindeutig ist, und dass präzise Vorhersagen möglich sind. Wenn die Lösung durch eine konvergente Reihenentwicklung gegeben ist, ist das ausreichend.
Physik muss nicht unbedingt zum Welt erklären, Physik muss präzise und experimentell überprüfbare Vorhersagen machen.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
positive
Anmeldungsdatum: 06.12.2013
Beiträge: 494
|
| positive Verfasst am: 22. Jan 2016 17:54 Titel: |
|
|
| TomS hat Folgendes geschrieben: | Ob die Lösung eines Problems mathematisch geschlossen formuliert werden kann, ist völlig irrelevant. Relevant und praktisch bedeutsam ist, dass eine Lösung prinzipiell existiert, eindeutig ist, und dass präzise Vorhersagen möglich sind. Wenn die Lösung durch eine konvergente Reihenentwicklung gegeben ist, ist das ausreichend.
Physik muss nicht unbedingt zum Welt erklären, Physik muss präzise und experimentell überprüfbare Vorhersagen machen. |
Warum? Angenommen die Weltformel wäre 20 Meter lang, das muss mathematisch geschlossen formuliert werden können und präzise die Welt "erklären". Einzelne Bauteile bzw. Theorien für sich alleine reichen da nicht. Es wird ja entsprechend versucht die ART und Quantenmechanik zu vereinen, was bis dato nicht gelungen ist. Man gibt sich in der Physik nicht zufrieden mit den einzelnen Theorien.
Inwieweit ist also der Artikel unsachlich bzw. er die aktuelle Situation nicht wiedergibt?
|
|
|
jh8979
Moderator
Anmeldungsdatum: 10.07.2012
Beiträge: 8575
|
| jh8979 Verfasst am: 22. Jan 2016 19:32 Titel: |
|
|
| positive hat Folgendes geschrieben: |
Inwieweit ist also der Artikel unsachlich bzw. er die aktuelle Situation nicht wiedergibt? |
Das hat Tom weiter vorne recht detailliert geschrieben... falls du dir die mühe machen magst das zu lesen....
|
|
|
positive
Anmeldungsdatum: 06.12.2013
Beiträge: 494
|
| positive Verfasst am: 22. Jan 2016 20:24 Titel: |
|
|
| jh8979 hat Folgendes geschrieben: | | positive hat Folgendes geschrieben: |
Inwieweit ist also der Artikel unsachlich bzw. er die aktuelle Situation nicht wiedergibt? |
Das hat Tom weiter vorne recht detailliert geschrieben... falls du dir die mühe machen magst das zu lesen.... |
Wie soll das was TomS schreibt denn gehen, ohne mathematische Formulierung, wie sollen Vorhersagen in der Physik ohne Mathematik präzisiert werden?
|
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18007
|
| TomS Verfasst am: 23. Jan 2016 10:33 Titel: |
|
|
| positive hat Folgendes geschrieben: | | Angenommen die Weltformel wäre 20 Meter lang, das muss mathematisch geschlossen formuliert werden können und präzise die Welt "erklären". |
99% der Physik befasst sich nicht mit der Weltformel und nicht mit der "Erklärung" der Welt, sondern ganz pragmatisch mit einzelnen, nicht fundamentalen Problemen.
Selbst wenn die Weltformel bekannt und geschlossen darstellbar wäre, würde das noch lange nicht für die Lösungen gelten. Bisher können wir für 'zig Theorien geschlossene Formeln angeben (Schrödingergleichung der nicht.-rel. QM, QED, QCD, ART, ...), jedoch für realistische Probleme nie geschlossene Lösungen.
| positive hat Folgendes geschrieben: | | Einzelne Bauteile bzw. Theorien für sich alleine reichen da nicht. Es wird ja entsprechend versucht die ART und Quantenmechanik zu vereinen, was bis dato nicht gelungen ist. Man gibt sich in der Physik nicht zufrieden mit den einzelnen Theorien. |
s.o. - 99% der Physiker befassen sich mit anderen Themen; und selbst eine Vereinheitlichung garantiert keine geschlossene Lösung.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18007
|
| TomS Verfasst am: 23. Jan 2016 10:36 Titel: |
|
|
| positive hat Folgendes geschrieben: | | Wie soll das was TomS schreibt denn gehen, ohne mathematische Formulierung, wie sollen Vorhersagen in der Physik ohne Mathematik präzisiert werden? |
Ich habe nicht gesagt, dass es ohne präzise Mathematik geht, sondern dass keine geschlossene Lösung gefunden werden kann; verstehst du den Unterschied? verstehst du, dass ich eine Theorie geschlossen formulieren, jedoch nicht notwendigerweise geschlossen lösen kann?
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
positive
Anmeldungsdatum: 06.12.2013
Beiträge: 494
|
| positive Verfasst am: 23. Jan 2016 12:00 Titel: |
|
|
| TomS hat Folgendes geschrieben: |
Ich habe nicht gesagt, dass es ohne präzise Mathematik geht, sondern dass keine geschlossene Lösung gefunden werden kann; verstehst du den Unterschied? verstehst du, dass ich eine Theorie geschlossen formulieren, jedoch nicht notwendigerweise geschlossen lösen kann? |
Mit "geschlossen formulieren" meinst du, dass du dies zunächst in Worten beschreibst? Und mit "geschlossen lösen" meinst du, dies mathematisch zu tun? Wie weiß man, ob die geschlossene Formulierung richtig ist? Was bringt das geschlossen zu formulieren aber nicht geschlossen zu lösen?
| TomS hat Folgendes geschrieben: | | 99% der Physik befasst sich nicht mit der Weltformel und nicht mit der "Erklärung" der Welt, sondern ganz pragmatisch mit einzelnen, nicht fundamentalen Problemen. |
Ja, ok. Es ist eher ein Theoriegebäude, wird auch so im Artikel genannt. Warum ist der Vergleich mit dem Turm von Babel unzutreffend, wenn er sagt, dass es teilweise Risse gibt, keine Lösungen, usw.?
|
|
|
as_string
Moderator
Anmeldungsdatum: 09.12.2005
Beiträge: 5785
Wohnort: Heidelberg
|
| as_string Verfasst am: 23. Jan 2016 12:15 Titel: |
|
|
| positive hat Folgendes geschrieben: |
Mit "geschlossen formulieren" meinst du, dass du dies zunächst in Worten beschreibst? Und mit "geschlossen lösen" meinst du, dies mathematisch zu tun? Wie weiß man, ob die geschlossene Formulierung richtig ist? Was bringt das geschlossen zu formulieren aber nicht geschlossen zu lösen? |
Nein, Blödsinn. Geschlossen formuliert meint natürlich auch mathematisch. Sieh es doch einfach ein: Du hast einfach keine Ahnung, um was es überhaupt geht und es ist lächerlich, dass Du Dich unter diesen Bedingungen immer als der große Skeptiker und Kritiker verstehst. Lass es doch einfach! Oder mach vorher ein Physik-Studium, damit Du ein paar Grundbegriffe kennen lernst und verstehst!
Gruß
Marco
|
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18007
|
| TomS Verfasst am: 23. Jan 2016 21:02 Titel: |
|
|
| positive hat Folgendes geschrieben: | | Mit "geschlossen formulieren" meinst du, dass du dies zunächst in Worten beschreibst? |
Mit "geschlossen formulieren" meine ich z.B.
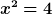
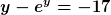
| positive hat Folgendes geschrieben: | | Und mit "geschlossen lösen" meinst du, dies mathematisch zu tun? |
Und mit "geschlossen lösen" meine ich dann
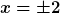
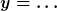
Im zweiten Fall existiert natürlich eine Lösung, aber keine geschlossene Lösung.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
Jayk
Anmeldungsdatum: 22.08.2008
Beiträge: 1450
|
| Jayk Verfasst am: 23. Jan 2016 22:15 Titel: |
|
|
| Jayk hat Folgendes geschrieben: | Wenn man sagt, die Gleichungen seien nicht lösbar, klingt das so, als ob die Gleichungen totaler Quatsch wären. Aber die Gleichungen sind lösbar, man kann eben bloß keine Lösung angeben. Nichtsdestoweniger kann man die Existenz einer Lösung beweisen.
Und verschwiegen wird das "Problem" wirklich nicht. Im Gegenteil: Es wird mehr Lärm darum gemacht, als es eigentlich verdient hätte. |
positive, nicht jede Funktion kann man explizit angeben. Man kann ja auch nicht jede Zahl explizit angeben, z.B. pi oder 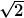 . Man kann aber die reellen Zahlen geeignet postulieren und auch konstruieren und diese haben eine sehr schöne Eigenschaft: Vollständigkeit. Das heißt, man kann 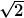als Grenzwert von solchen Zahlen, die man explizit angeben kann, angeben. Eine Möglichkeit, so eine Folge zu bekommen, ist das Heronsche Iterationsverfahren. Genauso kann man auch Lösungen von Differentialgleichungen durch Iteration gewinnen. Zum Beispiel kann man für die Differentialgleichung
)) mit  = a)
die äquivalente Integralgleichung
 = a + \int_0^t d\tau\,f(x(\tau )))
hernehmen und dann ausgehend von  = a) die Iterationsvorschrift
 := a + \int_0^t d\tau\,f(x_n (\tau )))
nehmen (Picard-Iteration) und unter sehr allgemeinen Bedingungen zeigen, daß diese konvergiert (als Hilfsmittel dient der Banachsche Fixpunktsatz, der entsprechende Satz für gewöhnliche Differentialgleichungen heißt Satz von Picard-Lindelöf).
[Anmerkung: Konvergenz bedeutet per definitionem(!), daß es einen Grenzwert gibt!]
Auch kann man kontrollieren, wie weit die Näherungslösungen von der exakten Lösung abweichen. Man hat also einen Rahmen, in dem experimentelle Ergebnisse liegen müssen, und damit eine falsifizierbare Theorie.
Zuletzt bearbeitet von Jayk am 23. Jan 2016 23:35, insgesamt einmal bearbeitet |
|
|
positive
Anmeldungsdatum: 06.12.2013
Beiträge: 494
|
| positive Verfasst am: 23. Jan 2016 22:41 Titel: |
|
|
| as_string hat Folgendes geschrieben: | | positive hat Folgendes geschrieben: |
Mit "geschlossen formulieren" meinst du, dass du dies zunächst in Worten beschreibst? Und mit "geschlossen lösen" meinst du, dies mathematisch zu tun? Wie weiß man, ob die geschlossene Formulierung richtig ist? Was bringt das geschlossen zu formulieren aber nicht geschlossen zu lösen? |
Nein, Blödsinn. Geschlossen formuliert meint natürlich auch mathematisch. Sieh es doch einfach ein: Du hast einfach keine Ahnung, um was es überhaupt geht und es ist lächerlich, dass Du Dich unter diesen Bedingungen immer als der große Skeptiker und Kritiker verstehst. Lass es doch einfach! Oder mach vorher ein Physik-Studium, damit Du ein paar Grundbegriffe kennen lernst und verstehst!
Gruß
Marco |
Ich frage ja nur. Bin kein Möchtegern so wie du der immer an der Sache vorbeiredet.
|
|
|
positive
Anmeldungsdatum: 06.12.2013
Beiträge: 494
|
| positive Verfasst am: 23. Jan 2016 22:49 Titel: |
|
|
| TomS hat Folgendes geschrieben: | | positive hat Folgendes geschrieben: | | Mit "geschlossen formulieren" meinst du, dass du dies zunächst in Worten beschreibst? |
Mit "geschlossen formulieren" meine ich z.B.
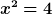
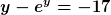
| positive hat Folgendes geschrieben: | | Und mit "geschlossen lösen" meinst du, dies mathematisch zu tun? |
Und mit "geschlossen lösen" meine ich dann
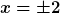
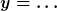
Im zweiten Fall existiert natürlich eine Lösung, aber keine geschlossene Lösung. |
Ok. Ich ging klar davon aus, dass man das Ganze auch mathematisch formuliert, aber du kennst ja das alte Problem. Möchtegerns suchen immer Ausreden, wenn die nicht mehr weiterwissen. Ist aber nicht auf dich bezogen momentan.
Was bringt jetzt also die zweite Gleichung, wenn ich keine geschlossene Lösung habe?
|
|
|
ML
Anmeldungsdatum: 17.04.2013
Beiträge: 3388
|
| ML Verfasst am: 23. Jan 2016 23:00 Titel: |
|
|
Hallo,
| Zitat: |
Möchtegerns suchen immer Ausreden, wenn die nicht mehr weiterwissen. Ist aber nicht auf dich bezogen momentan.
|
Aha, momentan also nicht. Das wird ihn sicher freuen.
| positive hat Folgendes geschrieben: |
Was bringt jetzt also die zweite Gleichung, wenn ich keine geschlossene Lösung habe? |
Es ist doch irgendwo klar, dass man mit dem begrenzten Vorrat an Funktionen, die einen eigenen Namen haben, nicht jedes Problem so elegant lösen kann, wie man das vielleicht gerne würde.
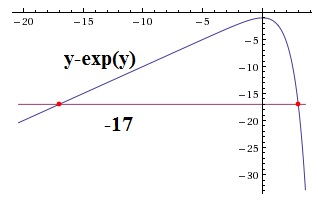
Insofern bist Du oft schon froh, wenn Du für ein mathematisch/physikalisch/technisches Problem überhaupt eine Gleichung aufschreiben kannst. So kannst Du zumindest nach Näherungslösungen suchen. Im Beispiel kannst Du sie auch leicht finden (siehe Plot).
Viele Grüße
Michael
| Beschreibung: |
|
| Dateigröße: |
14.4 KB |
| Angeschaut: |
5262 mal |
|
|
|
|
positive
Anmeldungsdatum: 06.12.2013
Beiträge: 494
|
| positive Verfasst am: 23. Jan 2016 23:25 Titel: |
|
|
| ML hat Folgendes geschrieben: |
| positive hat Folgendes geschrieben: |
Was bringt jetzt also die zweite Gleichung, wenn ich keine geschlossene Lösung habe? |
Es ist doch irgendwo klar, dass man mit dem begrenzten Vorrat an Funktionen, die einen eigenen Namen haben, nicht jedes Problem so elegant lösen kann, wie man das vielleicht gerne würde.
Insofern bist Du oft schon froh, wenn Du für ein mathematisch/physikalisch/technisches Problem überhaupt eine Gleichung aufschreiben kannst. So kannst Du zumindest nach Näherungslösungen suchen. Im Beispiel kannst Du sie auch leicht finden (siehe Plot).
Viele Grüße
Michael |
Ja, soviel Mathe kann ich schon noch ohne nachzurechnen. Ich wollte auf den Artikel und die Aussage des Autors und nicht auf die Näherungslösungen hinaus
|
|
|
Jayk
Anmeldungsdatum: 22.08.2008
Beiträge: 1450
|
| Jayk Verfasst am: 23. Jan 2016 23:33 Titel: |
|
|
| positive hat Folgendes geschrieben: | | Ich wollte auf den Artikel und die Aussage des Autors und nicht auf die Näherungslösungen hinaus |
Wie oft soll man es denn noch sagen: Die Aussage des Autors ist falsch!
Es gibt wenige Gleichungen, über deren Lösungen man nichts weiß. Die Navier-Stokes-Gleichung ist ein Beispiel, wenn Du dafür die Existenz von Lösungen beweisen oder widerlegen kannst, kannst Du sehr viel Geld verdienen. Die vom Autor genannten Beispiele gehören aber ganz sicher nicht dazu!
|
|
|
positive
Anmeldungsdatum: 06.12.2013
Beiträge: 494
|
| positive Verfasst am: 23. Jan 2016 23:58 Titel: |
|
|
| Jayk hat Folgendes geschrieben: |
Wie oft soll man es denn noch sagen: Die Aussage des Autors ist falsch!
Es gibt wenige Gleichungen, über deren Lösungen man nichts weiß. Die Navier-Stokes-Gleichung ist ein Beispiel, wenn Du dafür die Existenz von Lösungen beweisen oder widerlegen kannst, kannst Du sehr viel Geld verdienen. Die vom Autor genannten Beispiele gehören aber ganz sicher nicht dazu! |
Der Autor sagt z.B., dass man häufig nicht einmal wisse, ob eine gefundene Lösung korrekt sei, weil die Langrange-Methode beim Doppelpendel nicht mehr so simpel sei, wenn sich die Länge der Seile mit der Zeit ändert.
Das meinte ich, um bei simplen Sachen zu bleiben.
|
|
|
jh8979
Moderator
Anmeldungsdatum: 10.07.2012
Beiträge: 8575
|
| jh8979 Verfasst am: 24. Jan 2016 10:43 Titel: |
|
|
| positive hat Folgendes geschrieben: | | Bin kein Möchtegern so wie du der immer an der Sache vorbeiredet. |
Doch bist Du. Daher gibt es jetzt von mir wieder die gelbe Karte. Du weisst ja was bei einer roten passiert...
|
|
|
Jayk
Anmeldungsdatum: 22.08.2008
Beiträge: 1450
|
| Jayk Verfasst am: 24. Jan 2016 12:54 Titel: |
|
|
| positive hat Folgendes geschrieben: | Der Autor sagt z.B., dass man häufig nicht einmal wisse, ob eine gefundene Lösung korrekt sei, weil die Langrange-Methode beim Doppelpendel nicht mehr so simpel sei, wenn sich die Länge der Seile mit der Zeit ändert.
Das meinte ich, um bei simplen Sachen zu bleiben. |
Der Autor beschreibt eine Feder. Das stellt kein Problem für die Lagrange-Methode dar.
|
|
|
positive
Anmeldungsdatum: 06.12.2013
Beiträge: 494
|
| positive Verfasst am: 24. Jan 2016 13:19 Titel: |
|
|
| Jayk hat Folgendes geschrieben: | | positive hat Folgendes geschrieben: | Der Autor sagt z.B., dass man häufig nicht einmal wisse, ob eine gefundene Lösung korrekt sei, weil die Langrange-Methode beim Doppelpendel nicht mehr so simpel sei, wenn sich die Länge der Seile mit der Zeit ändert.
Das meinte ich, um bei simplen Sachen zu bleiben. |
Der Autor beschreibt eine Feder. Das stellt kein Problem für die Lagrange-Methode dar. |
Das kann ich so nirgendwo lesen. Ich beziehe mich auf Seite 64. Kannst du das mal reinstellen wo die Stelle mit der Feder ist?
|
|
|
Jayk
Anmeldungsdatum: 22.08.2008
Beiträge: 1450
|
| Jayk Verfasst am: 24. Jan 2016 13:54 Titel: |
|
|
Ach, okay. Ich dachte, Du beziehst Dich auf Seite 63.
Macht aber auch nichts. Selbst ein Labber-Seil kannst Du mit dem Lagrange-Formalismus beschreiben. Das ist dann ein bißchen komplizierter, weil Du dann eine Feldtheorie mit unendlich vielen Freiheitsgraden hast, aber prinzipiell möglich. Bücher wie der Scheck oder der Marsden/Rațiu behandeln auch kontinuierliche Systeme.
|
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18007
|
| TomS Verfasst am: 24. Jan 2016 15:50 Titel: |
|
|
| positive hat Folgendes geschrieben: | | Was bringt jetzt also die zweite Gleichung, wenn ich keine geschlossene Lösung habe? |
Es ist vollkommen irrelevant, ob eine Gleichung eine geschlossene Lösung hat. Viel wichtiger ist, ob eine Lösung existiert und ob diese exakt berechenbar ist. Letzteres ist im Falle der zweiten Gleichung der Fall.
Die geschlossene Lösung einer Gleichung im Sinne von
)
mag dir bekannt und daher sinnvoll vorkommen; und
)
mag dir schöner erscheinen als
})
Aber das ist völlig irrelevant, denn beides bezeichnet mathematisch das selbe.
Für das Pendel existiert gemäß dem o.g. Artikel lediglich eine Näherungslösung für kleine Winkel
 = \phi_0\,\cos(\omega t + \delta))
Tatsache ist, dass eine exakte und geschlossene Lösung für beliebige Winkel existiert, nämlich mittels elliptischer Integrale; allerdings sind diese nur Experten vertraut, und werden damit für Laien nicht als "geschlossen" bezeichnet. Sind diese Lösungen jetzt schlechter, nur weil sie komplizierter sind?
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
positive
Anmeldungsdatum: 06.12.2013
Beiträge: 494
|
| positive Verfasst am: 24. Jan 2016 18:01 Titel: |
|
|
| Jayk hat Folgendes geschrieben: | Ach, okay. Ich dachte, Du beziehst Dich auf Seite 63.
Macht aber auch nichts. Selbst ein Labber-Seil kannst Du mit dem Lagrange-Formalismus beschreiben. Das ist dann ein bißchen komplizierter, weil Du dann eine Feldtheorie mit unendlich vielen Freiheitsgraden hast, aber prinzipiell möglich. Bücher wie der Scheck oder der Marsden/Rațiu behandeln auch kontinuierliche Systeme. |
Was ist ein Labber-Seil?
Der Autor meint, dass einem Physiker spätestens dann die Freude am Problem verginge, wenn man das Seil durch eine Feder ersetze. Kannst du evtl. ein Beispiel für eine sogenannte exakte Lösung dieses Pendels mit einer Feder vorzeigen?
|
|
|
positive
Anmeldungsdatum: 06.12.2013
Beiträge: 494
|
| positive Verfasst am: 24. Jan 2016 18:18 Titel: |
|
|
| TomS hat Folgendes geschrieben: |
Tatsache ist, dass eine exakte und geschlossene Lösung für beliebige Winkel existiert, nämlich mittels elliptischer Integrale; allerdings sind diese nur Experten vertraut, und werden damit für Laien nicht als "geschlossen" bezeichnet. Sind diese Lösungen jetzt schlechter, nur weil sie komplizierter sind? |
Der Autor ist ein Experte und meint aber, dass es gar keine exakten Lösungen gäbe, jedenfalls nicht im Sinne elementarer Funktionen wie Sinus, Cosinus. Auch soll mal lange darüber diskutieren können, ob "exakt" bei der Kompliziertheit der mathematischen Thermen überhaupt noch zutreffend sei.
Exakt im Fall des Doppelpendels ist im Sinne der Realität so zu verstehen, dass bei entsprechenden Anfangsbedingungen vorherzusagen ist, was es zu beliebigen Zeitpunkten macht. Es geht weniger um Schönheit oder Komplexität von Formeln, sondern, ob "exakt" mit der Realität übereinstimmt. Warum ist das unzutreffend was der Autor sagt. Kannst du anhand eines Pendelbeispiels dies evtl. genauer erklären?
|
|
|
schnudl
Moderator
Anmeldungsdatum: 15.11.2005
Beiträge: 6979
Wohnort: Wien
|
| schnudl Verfasst am: 24. Jan 2016 18:37 Titel: |
|
|
| positive hat Folgendes geschrieben: |
Der Autor meint, dass einem Physiker spätestens dann die Freude am Problem verginge, wenn man das Seil durch eine Feder ersetze. Kannst du evtl. ein Beispiel für eine sogenannte exakte Lösung dieses Pendels mit einer Feder vorzeigen? |
Ob man das mit Lagrange-Formalismus löst oder anders ist unerheblich. Die Differentialgleichungen sind die gleichen. Geschlossen lösbar ist natürlich nicht alles, aber wo spielt das in dem Kontext eine Rolle? Niemand erwartet das auch...Hier wird den Physikern eine Haltung unterstellt, die unrichtig ist. Solange man ein physikalisches System PRINZIPIELL vorhersagend beschreiben kann, ist das doch toll, unabhängig von der Art des Lösungsansätzes für die Rechnung.
_________________
Wenn du eine weise Antwort verlangst, musst du vernünftig fragen (Goethe) |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18007
|
| TomS Verfasst am: 24. Jan 2016 19:19 Titel: |
|
|
| positive hat Folgendes geschrieben: | | TomS hat Folgendes geschrieben: | | Tatsache ist, dass eine exakte und geschlossene Lösung für beliebige Winkel existiert, nämlich mittels elliptischer Integrale; allerdings sind diese nur Experten vertraut, und werden damit für Laien nicht als "geschlossen" bezeichnet. Sind diese Lösungen jetzt schlechter, nur weil sie komplizierter sind? |
Der Autor ist ein Experte und meint aber, dass es gar keine exakten Lösungen gäbe, jedenfalls nicht im Sinne elementarer Funktionen wie Sinus, Cosinus. Auch soll mal lange darüber diskutieren können, ob "exakt" bei der Kompliziertheit der mathematischen Thermen überhaupt noch zutreffend sei. |
Bitte unterscheide exakt und geschlossen. Exakt bedeutet, dass ich den Wert bzw. die Lösung ohne Näherung bzw. beliebig genau angeben kann. Geschlossen bedeutet, dass ich eine "elementare Funktion" hinschreiben kann. Wenn keine "elementare Funktion" und damit keine geschlossene Lösung existiert, kann immer noch eine exakte Lösung existieren. Z.B. werden viele Probleme durch eine Reihenentwicklung gelöst; aber auch ein Sinus ist letztlich nur eine Reihenentwicklung.
Wenn keine exakte Lösung sondern nur eine Näherungslösung bekannt ist, dann ist das grundsätzlich auch kein Problem, da man die Näherung üblicherweise prinzipiell beliebig verbessern kann, nämlich wenn die Näherungsmethode konvergiert. Z.B. sind die meisten Probleme der QM nur näherungsweise und demnach zunächst weder exakt noch geschlossen lösbar, jedoch aufgrund der (beweisbaren) Konvergenzeigenschaften der Störungstheorie mit beliebiger Genauigkeit. Damit ist die fehlende Exaktheit völlig unkritisch, ich kann prinzipiell jede beliebige Genauigkeit erreichen. Nichts anderes macht der Taschenrechner mit dem Sinus.
| positive hat Folgendes geschrieben: | | Exakt im Fall des Doppelpendels ist im Sinne der Realität so zu verstehen, dass bei entsprechenden Anfangsbedingungen vorherzusagen ist, was es zu beliebigen Zeitpunkten macht. Es geht weniger um Schönheit oder Komplexität von Formeln, sondern, ob "exakt" mit der Realität übereinstimmt. Warum ist das unzutreffend was der Autor sagt. Kannst du anhand eines Pendelbeispiels dies evtl. genauer erklären? |
Im Falle eines komplizierten (hier: chaotischen) Systems ist zunächst keine geschlossene Lösung verfügbar. Außerdem sind i.A. die Anfangsbedingungen nicht exakt bekannt, und demnach auch nicht die Lösung.
Das wesentliche Problem bei einem chaotischen System ist, dass kleine Abweichungen in den Anfangsbedingungen zu großen Abweichungen in den Lösungen führen. Üblicherweise bleiben Abweichungen klein, nicht so bei Chaos. D.h. dass übliche Näherungsmethoden versagen bzw. nicht auf beliebige Zeiträume angewandt werden können.
Ich sehe darin aber kein prinzipielles Problem, lediglich ein praktisches; wenn die Anfangsbedingungen exakt benannt wären und wenn Computer mit beliebiger Genauigkeit rechnen könnten, dann würden auch die Ergebnisse exakt folgen, d.h. es läge Exaktheit vor. Das Problem liegt in der angewandten Methode, nicht im System selbst.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18007
|
| TomS Verfasst am: 24. Jan 2016 19:21 Titel: |
|
|
Das ist alles aber überhaupt nicht das Problem, das wir mit dem Artikel haben!
Der Autor suggeriert, die Physiker wären sich dieser Probleme nicht bewusst, würden sie unter den Teppich kehren oder sonst irgendwie schummeln. Es klingt so, als würden Physiker lügen und betrügen. Aber das stimmt nicht. Ich würde sogar sagen, das ist glatt gelogen!
Die Physiker sind sich der Probleme bewusst: sie kennen und verstehen die Grenzen von Näherungslösungen; sie versuchen, diese zu verbessern; sie geben für ihre Resultaten die jeweiligen Fehlerbalken an, die aus Näherungen resultieren; sie wissen, was Chaos ist, sie verstehen das zeitliche Divergieren zweier näherungsweiser identischer Anfangsbedingungen; sie wissen, dass die Störungstheorie der QFT nur eine asymptotische Reihenentwicklung darstellt, sie arbeiten an Alternativen, ...
Physiker ticken anders und argumentieren anders, als der Autor uns glauben machen will. Ich weiß nicht, welche Physiker der Autor meint (ich habe lediglich eine Vermutung) jedenfalls nicht mein (ehemaliges) Umfeld.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
positive
Anmeldungsdatum: 06.12.2013
Beiträge: 494
|
| positive Verfasst am: 24. Jan 2016 20:29 Titel: |
|
|
| TomS hat Folgendes geschrieben: | | Wenn keine exakte Lösung sondern nur eine Näherungslösung bekannt ist, dann ist das grundsätzlich auch kein Problem, da man die Näherung üblicherweise prinzipiell beliebig verbessern kann, nämlich wenn die Näherungsmethode konvergiert. |
Insgesamt betrachtet ist das alles was du sagst, aber trotzdem nicht exakt. Man kann z.B. nicht unendlich lange konvergieren. Und geschlossen ist dann offensichtlich auch nichts, denn wenn eine "elementare Funktion" auch nicht exakt ist, weil sie nur eine Reihenentwicklung ist, ist die Definition von geschlossen auch ungenau.
| TomS hat Folgendes geschrieben: | Außerdem sind i.A. die Anfangsbedingungen nicht exakt bekannt, und demnach auch nicht die Lösung.
|
Warum nicht? Ich ziehe das Pendel und lasse es los, dann ist die Anfangsbedingung in der Realität exakt und bekannt. Ansonsten braucht man nicht nach der Lösung zu suchen.
| TomS hat Folgendes geschrieben: | | wenn die Anfangsbedingungen exakt benannt wären und wenn Computer mit beliebiger Genauigkeit rechnen |
Sicher, das Problem ist jedoch, dass du diese nur dann kennst, wenn du es schaffst aus den Abweichungen bzw. unexakt auf exakte Anfangsbedingungen zu schließen. Wie willst du das anstellen?
Nach meiner Ansicht hat der Autor aufgrund mancher Unmöglichkeiten die Stellung der Physik richtig erkannt auf dem Weg zum (besseren) Verständnis der Natur. Natürlich darf jeder seine eigene Meinung haben wenn ihm eine Näherungslösung gut genug ist.
| TomS hat Folgendes geschrieben: | | Der Autor suggeriert, die Physiker wären sich dieser Probleme nicht bewusst, würden sie unter den Teppich kehren oder sonst irgendwie schummeln. Es klingt so, als würden Physiker lügen und betrügen. Aber das stimmt nicht. Ich würde sogar sagen, das ist glatt gelogen! |
Als ich meine Antwort schrieb, habe ich deinen letzten Beitrag nicht gesehen. Ich kann das nicht beurteilen, inwieweit Betrug oder Schummelei in der Physik vorhanden sein mag oder warum der Artikel aus deiner Sicht so hart verfasst wurde.
|
|
|
DrStupid
Anmeldungsdatum: 07.10.2009
Beiträge: 5040
|
| DrStupid Verfasst am: 24. Jan 2016 21:08 Titel: |
|
|
| positive hat Folgendes geschrieben: | | Insgesamt betrachtet ist das alles was du sagst, aber trotzdem nicht exakt. Man kann z.B. nicht unendlich lange konvergieren. |
Wozu auch? Die Rechnung muss nur so exakt sein, wie die experimentelle Beobachtung.
| positive hat Folgendes geschrieben: | | Ich ziehe das Pendel und lasse es los, dann ist die Anfangsbedingung in der Realität exakt und bekannt. |
Sie ist nur so gut bekannt, wie Du sie messen kannst.
| positive hat Folgendes geschrieben: | Nach meiner Ansicht hat der Autor aufgrund mancher Unmöglichkeiten die Stellung der Physik richtig erkannt auf dem Weg zum
(besseren) Verständnis der Natur. |
Persönliche Meinungen sind in der Physik irrelevant.
|
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18007
|
| TomS Verfasst am: 24. Jan 2016 21:27 Titel: |
|
|
| DrStupid hat Folgendes geschrieben: | | Persönliche Meinungen sind in der Physik irrelevant. |
Sehe ich nicht so; ich bin z.B. persönlich der Meinung, dass positive keine Ahnung von Physik hat
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
positive
Anmeldungsdatum: 06.12.2013
Beiträge: 494
|
| positive Verfasst am: 24. Jan 2016 22:24 Titel: |
|
|
| DrStupid hat Folgendes geschrieben: | | positive hat Folgendes geschrieben: | | Insgesamt betrachtet ist das alles was du sagst, aber trotzdem nicht exakt. Man kann z.B. nicht unendlich lange konvergieren. |
Wozu auch? Die Rechnung muss nur so exakt sein, wie die experimentelle Beobachtung.
| positive hat Folgendes geschrieben: | | Ich ziehe das Pendel und lasse es los, dann ist die Anfangsbedingung in der Realität exakt und bekannt. |
Sie ist nur so gut bekannt, wie Du sie messen kannst. |
Ja, aber Deine beiden Aussagen widersprechen sich ein wenig. Du kannst nicht einmal sagen, die Genauigkeit ist genau genug aufgrund der Beobachtung und einmal sagen, naja ich kann zwar nichts vorhersagen, aber ich könnte es, wenn ich besser messen könnte. Es ist eine unphysikalische Aussage. Da könnte jemand auf die Idee kommen und dir sagen, komm wieder wenn du die Anfangsbedingungen exakt messen kannst.
| DrStupid hat Folgendes geschrieben: | | Persönliche Meinungen sind in der Physik irrelevant. |
Kommt drauf an. Mir ging es aber um den Artikel an sich. Möglich dass der Autor sich tiefere Gedanken über die Natur gemacht hat und mit den Antworten unzufrieden war. Ich denke, dies geht aus dem Artikel ein bißchen auch hervor.
|
|
|
positive
Anmeldungsdatum: 06.12.2013
Beiträge: 494
|
| positive Verfasst am: 24. Jan 2016 22:28 Titel: |
|
|
| TomS hat Folgendes geschrieben: |
Sehe ich nicht so; ich bin z.B. persönlich der Meinung, dass positive keine Ahnung von Physik hat |
Ich bin der Meinung, dass es eine gute Unterhaltung mit dir und den anderen war.
|
|
|
as_string
Moderator
Anmeldungsdatum: 09.12.2005
Beiträge: 5785
Wohnort: Heidelberg
|
| as_string Verfasst am: 24. Jan 2016 22:30 Titel: |
|
|
| positive hat Folgendes geschrieben: | | Da könnte jemand auf die Idee kommen und dir sagen, komm wieder wenn du die Anfangsbedingungen exakt messen kannst. |
Du kannst nie exakt messen! Deshalb gibt man immer eine Messungenauigkeit an.
Komm wieder, wenn Du ein paar Grundbegriffe der Physik verstanden hast. Es nervt einfach nur noch..
Gruß
Marco
|
|
|
Jayk
Anmeldungsdatum: 22.08.2008
Beiträge: 1450
|
| Jayk Verfasst am: 24. Jan 2016 22:32 Titel: |
|
|
| positive hat Folgendes geschrieben: | | Man kann z.B. nicht unendlich lange konvergieren. |
positive, Du hast keinen blassen Schimmer, was Du da sagst.
Konvergenz bedeutet per definitionem, daß es einen Grenzwert gibt, wobei in jeder noch so kleinen Umgebung dieses Grenzwerts alle bis auf endlich viele Folgenglieder liegen. Dieser ist dann auch immer eindeutig, wie man normalerweise in der 10. Klasse Gymnasium in Mathe lernt. Ich frage mich, wo Du da warst...
Von Konvergenz zu sprechen, ist überhaupt nur dann sinnvoll, wenn es unendlich viele Folgenglieder gibt.
https://de.wikipedia.org/wiki/Grenzwert_%28Folge%29
https://de.wikipedia.org/wiki/Cauchy-Folge
https://de.wikipedia.org/wiki/Vollst%C3%A4ndiger_Raum
https://de.wikipedia.org/wiki/Irrationale_Zahl
https://de.wikipedia.org/wiki/Funktion_%28Mathematik%29#Begriffsgeschichte
https://de.wikipedia.org/wiki/Satz_von_Picard-Lindelöf
Vermutlich sind auch irrationale Zahlen wie ^n) nicht exakt definiert. Vermutlich sind die ganzen Prozesse der Analysis wie Differentiation und Integration auch nicht exakt definiert. Wahrscheinlich schreiben die Mathematiker die Beweise, die Du in jedem Analysis-Lehrbuch finden kannst, einfach zur Unterhaltung auf... Soo unterhaltsam sind sie in den allermeisten Fällen nun doch nicht.^^
Zuletzt bearbeitet von Jayk am 24. Jan 2016 22:33, insgesamt einmal bearbeitet |
|
|
positive
Anmeldungsdatum: 06.12.2013
Beiträge: 494
|
| positive Verfasst am: 24. Jan 2016 22:33 Titel: |
|
|
| as_string hat Folgendes geschrieben: | | positive hat Folgendes geschrieben: | | Da könnte jemand auf die Idee kommen und dir sagen, komm wieder wenn du die Anfangsbedingungen exakt messen kannst. |
Du kannst nie exakt messen! Deshalb gibt man immer eine Messungenauigkeit an.
Komm wieder, wenn Du ein paar Grundbegriffe der Physik verstanden hast. Es nervt einfach nur noch..
Gruß
Marco |
Ich habe auch nicht gesagt, dass man exakt messen kann und auch nicht, der Teilnehmer DrStupid solle wiederkommen wenn er exakt messen könne. Ich sagte jemand. ;-)
|
|
|
positive
Anmeldungsdatum: 06.12.2013
Beiträge: 494
|
| positive Verfasst am: 24. Jan 2016 22:37 Titel: |
|
|
| Jayk hat Folgendes geschrieben: | | Von Konvergenz zu sprechen, ist überhaupt nur dann sinnvoll, wenn es unendlich viele Folgenglieder gibt. |
Was ja anzunehmen ist, wenn TomS meint, er könne beliebig genau messen.
Komm wieder wenn du sachlich und im Kontext und nicht zusammenhanglos wie jetzt argumentierst.
|
|
|
Jayk
Anmeldungsdatum: 22.08.2008
Beiträge: 1450
|
| Jayk Verfasst am: 24. Jan 2016 22:42 Titel: |
|
|
| positive hat Folgendes geschrieben: | | Jayk hat Folgendes geschrieben: | | Von Konvergenz zu sprechen, ist überhaupt nur dann sinnvoll, wenn es unendlich viele Folgenglieder gibt. |
Was ja anzunehmen ist, wenn TomS meint, er könne beliebig genau messen. |
Unsinn.
| Zitat: |
Komm wieder wenn du sachlich und im Kontext und nicht zusammenhanglos wie jetzt argumentierst. |
Komm wieder, wenn Du was gelernt hast. Es ist nicht meine Schuld, daß Du den Zusammenhang nicht verstehst, weil Du offensichtlich in der Schule gepennt hast. Ob eine Differentialgleichung eine Lösung hat oder nicht, ist eine mathematische Frage, die eine mathematische Antwort besitzt (Picard-Lindelöf). Was der Zusammenhang zur Meßgenauigkeit ist, habe u.a. ich weiter oben bereits sehr ausführlich dargelegt.
Zuletzt bearbeitet von Jayk am 24. Jan 2016 22:51, insgesamt einmal bearbeitet |
|
|
positive
Anmeldungsdatum: 06.12.2013
Beiträge: 494
|
| positive Verfasst am: 24. Jan 2016 22:50 Titel: |
|
|
| Jayk hat Folgendes geschrieben: | | positive hat Folgendes geschrieben: | | Jayk hat Folgendes geschrieben: | | Von Konvergenz zu sprechen, ist überhaupt nur dann sinnvoll, wenn es unendlich viele Folgenglieder gibt. |
Was ja anzunehmen ist, wenn TomS meint, er könne beliebig genau messen. |
Unsinn.
| Zitat: |
Komm wieder wenn du sachlich und im Kontext und nicht zusammenhanglos wie jetzt argumentierst. |
Komm wieder, wenn Du was gelernt hast. |
Du hast nicht unendlich viel Zeit zur Verfügung, um beliebig genau zu messen. So wird man nie den Wert erfahren. So war das gemeint. Hast du das nun verstanden?
|
|
|
Jayk
Anmeldungsdatum: 22.08.2008
Beiträge: 1450
|
| Jayk Verfasst am: 24. Jan 2016 22:52 Titel: |
|
|
|
Einen Verweis auf die Antwort findest Du in meinem Edit.
|
|
|
|
|
Registrieren
Login
FAQ
Suchen
