| Autor |
Nachricht |
Quantenmechaniker
Gast
|
 Quantenmechaniker Verfasst am: 07. Nov 2015 13:06 Titel: Quantenmechanik und Lie-Algebra Quantenmechaniker Verfasst am: 07. Nov 2015 13:06 Titel: Quantenmechanik und Lie-Algebra |
 |
|
Hallo
Ich habe mich hobbymäßig schon viel mit der Quantenmechanik beschäftigt. Am Rande tauchte immer mal der Begriff der Lie-Algebra auf, womit ich mich aber nicht weiter beschäftigt haben. Ich würde aber gern den Zusammenhang von der Quantenmechanik zur Lie-Algebra wissen.
Soweit ich weiß braucht man für eine Liealgebra einen  -Vektorraum mit einer Verknüpfung, die Lie-Klammer heißt bzw. was in der Quantenmechanik dann meistens durch den Kommutator realisiert ist. -Vektorraum mit einer Verknüpfung, die Lie-Klammer heißt bzw. was in der Quantenmechanik dann meistens durch den Kommutator realisiert ist.
Jetzt hat man bspw die Kommutatorrelationen des Drehimpulses

Für eine Lie-Algebra müssten doch jetzt die Drehimpulsoperatoren Elemente eines  -Vektorraums sein. Heißt das die Operatoren spannen solch einen Vektorraum auf und die Komponenten des Drehimpulsoperators sind die Basis? Also dass ein beliebiges Element dieses Vektorraums durch -Vektorraums sein. Heißt das die Operatoren spannen solch einen Vektorraum auf und die Komponenten des Drehimpulsoperators sind die Basis? Also dass ein beliebiges Element dieses Vektorraums durch  mit a, b und c als komplexe Zahlen gegeben ist? Ich finde das komisch, weil ich kenne in der Quantenmechanik nur die kets als Vektorraum, aber es sind ja nicht die kets welche man in einen Kommutator bzw einer Lie Klammer packt. Kann mich hier jemand aufklären? mit a, b und c als komplexe Zahlen gegeben ist? Ich finde das komisch, weil ich kenne in der Quantenmechanik nur die kets als Vektorraum, aber es sind ja nicht die kets welche man in einen Kommutator bzw einer Lie Klammer packt. Kann mich hier jemand aufklären?
Ich finde auch keine Literatur dazu, die für mich gut ist. Entweder ist sie so mathematisch und abstrakt, dass ich es nicht verstehe oder so einfach, dass meine Fragen nicht wirklich beantwortet werden.
Vielen Dank |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 07. Nov 2015 17:21 Titel: Re: Quantenmechanik und Lie-Algebra index_razor Verfasst am: 07. Nov 2015 17:21 Titel: Re: Quantenmechanik und Lie-Algebra |
 |
|
| Quantenmechaniker hat Folgendes geschrieben: | Hallo
Ich habe mich hobbymäßig schon viel mit der Quantenmechanik beschäftigt. Am Rande tauchte immer mal der Begriff der Lie-Algebra auf, womit ich mich aber nicht weiter beschäftigt haben. Ich würde aber gern den Zusammenhang von der Quantenmechanik zur Lie-Algebra wissen.
|
Das ist ein ziemlich weitläufiges Thema. Vielleicht der wichtigste Zusammenhang wird, würde ich sagen, über die Darstellungstheorie von Gruppen und Lie-Algebren vermittelt. Die vorkommenden Lie-Algebren sind normalerweise "infinitesimale" Symmetrietransformationen, erzeugen also Lie-Gruppen, die eine Darstellung auf dem Hilbert-Raum besitzen. Zustände können nach ihrem Transformationsverhalten unter dieser Darstellung klassifiziert werden. So kann man z.B. wichtige Aussagen über das System gewinnen (Energiespektrum, Auswahlregeln, Entartung, etc.) ohne die Schrödingergleichung im Detail lösen zu müssen.
| Zitat: |
Jetzt hat man bspw die Kommutatorrelationen des Drehimpulses

Für eine Lie-Algebra müssten doch jetzt die Drehimpulsoperatoren Elemente eines  -Vektorraums sein. Heißt das die Operatoren spannen solch einen Vektorraum auf und die Komponenten des Drehimpulsoperators sind die Basis? Also dass ein beliebiges Element dieses Vektorraums durch -Vektorraums sein. Heißt das die Operatoren spannen solch einen Vektorraum auf und die Komponenten des Drehimpulsoperators sind die Basis? Also dass ein beliebiges Element dieses Vektorraums durch  mit a, b und c als komplexe Zahlen gegeben ist? mit a, b und c als komplexe Zahlen gegeben ist?
|
Ja, die Drehimpulsalgebra wird allerdings typischerweise als reeller Vektorraum aufgefaßt, nicht als komplexer. Die Koeffizienten a,b,c definieren ja im Prinzip eine Drehrichtung im Raum relativ zur gewählten Basis. Ansonsten hast du aber im Prinzip recht. Die Operatoren  sind eine Basis der Algebra. Es gibt aber natürlich noch beliebig viele andere Basen. sind eine Basis der Algebra. Es gibt aber natürlich noch beliebig viele andere Basen.
| Zitat: |
Ich finde das komisch, weil ich kenne in der Quantenmechanik nur die kets als Vektorraum, aber es sind ja nicht die kets welche man in einen Kommutator bzw einer Lie Klammer packt. Kann mich hier jemand aufklären?
|
Ich verstehe nicht, was daran komisch ist. Lineare Strukturen tauchen immer wieder an verschiedenen Stellen auf. Daß der Hilbertraum selbst ein Vektorraum ist, hindert ja nicht die Drehimpulsalgebra daran, auch einer zu sein.
| Zitat: |
Ich finde auch keine Literatur dazu, die für mich gut ist. Entweder ist sie so mathematisch und abstrakt, dass ich es nicht verstehe oder so einfach, dass meine Fragen nicht wirklich beantwortet werden.
|
Zu welchen deiner Fragen konntest du denn keine Antwort finden? Mir fällt jetzt auch keine wirklich empfehlenswerte Lektüre ein, ohne noch genauer zu wissen in welche Richtung dein Interesse an dem Thema genau geht. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18062
|
 TomS Verfasst am: 08. Nov 2015 08:58 Titel: TomS Verfasst am: 08. Nov 2015 08:58 Titel: |
 |
|
Die Generatoren L der so(3) - oder verallgemeinert der su(2) - Algebra, definieren formal tatsächlich einen Vektorraum. Die Frage ist doch, welche Bedeutung einem allgemeinen Element G dieses Vektorraumes zukommt.
Dazu betrachtet man


Wie man leicht nachweist, ist U ein unitärer Operator, der eine Rotation mit Drehwinkeln theta auf den l-Darstellungen der Algebra erzeugt (das entspricht einer Drehung auf dem 2l+1 dimensionalen Vektorraum, aufgespannt durch die Kets |l,m> Zu festem l).
Übersetzt man dies in Wellenfunktionen, so folgt
 = \langle \Omega|\psi\rangle)
 = \langle \Omega |U[\theta]| \psi\rangle)
Omega steht für die Winkel theta, phi in sphärischen Koordinaten; die Radialkoordinate r ist irrelevant, da die Rotation nicht auf r wirkt; U ist der oben eingeführte Rotationsoperator; R ist eine entsprechende Rotationsmatrix, die auf das Argument Omega der Wellenfunktion psi wirkt, d.h. einer Rotation U auf den Kets kann eine entsprechende Rotation R im Ortsraum zugeordnet werden.
Der Zusammenhang zwischen den Kets |lm> als Basis des abstrakten Vektorraumes und einer Basis für die Wellenfunktionen in Ortsdarstellung folgt mittels der Kugelflächenfunktionen
 = \langle \Omega | lm\rangle)
 = \sum_{lm} \psi_{lm}\,Y_{lm}(\Omega))
G als Element der Algebra erzeugt also die Rotation U, die ein Element der Gruppe darstellt. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 08. Nov 2015 11:31 Titel: index_razor Verfasst am: 08. Nov 2015 11:31 Titel: |
 |
|
Die Koeffizienten in Linearkombinationen von Generatoren haben nicht die Bedeutung von Drehwinkeln. Das kann man sich daran klar machen, daß Drehwinkel im allgemeinen nur modulo 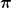 oder oder 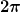 definiert sein können, die Algebra aber Linearkombinationen mit beliebigen Koeffizienten erlaubt und dabei definiert sein können, die Algebra aber Linearkombinationen mit beliebigen Koeffizienten erlaubt und dabei  nicht dasselbe Element ergibt wie nicht dasselbe Element ergibt wie  (auch wenn es dieselbe Drehung erzeugt). (auch wenn es dieselbe Drehung erzeugt).
| TomS hat Folgendes geschrieben: | Die Generatoren L der so(3) - oder verallgemeinert der su(2) - Algebra, definieren formal tatsächlich einen Vektorraum. Die Frage ist doch, welche Bedeutung einem allgemeinen Element G dieses Vektorraumes zukommt.
Dazu betrachtet man


Wie man leicht nachweist, ist U ein unitärer Operator, der eine Rotation mit Drehwinkeln theta auf den l-Darstellungen der Algebra erzeugt (das entspricht einer Drehung auf dem 2l+1 dimensionalen Vektorraum, aufgespannt durch die Kets |l,m> Zu festem l).
|
 dreht aber nicht jeweils im Winkel dreht aber nicht jeweils im Winkel 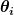 um die Achse um die Achse 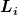 , sondern um den Winkel , sondern um den Winkel

um die Achse 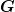 . Dies läßt sich möglicherweise als sukzessive Drehungen um die einzelnen Achsen schreiben . Dies läßt sich möglicherweise als sukzessive Drehungen um die einzelnen Achsen schreiben

aber die Drehwinkel  entsprechen dann nicht den Koeffizienten entsprechen dann nicht den Koeffizienten 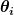 . .
Die Bedeutung der Vektorraumstruktur der so(3) liegt in der adjungierten Darstellung der SO(3) begründet, also in der Tatsache, daß Drehungen und infinitesimale Drehungen selbst wieder gedreht werden können. Dabei stellt man fest, daß sich jedes Element aus so(3) genauso transformiert wie ein gewöhnlicher Vektor im 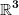 , also eine ganz normale Richtung im Raum definiert. Die Koeffizienten in , also eine ganz normale Richtung im Raum definiert. Die Koeffizienten in  transformieren also insbesondere linear unter SO(3), was für Drehwinkel nicht der Fall sein kann. transformieren also insbesondere linear unter SO(3), was für Drehwinkel nicht der Fall sein kann. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18062
|
 TomS Verfasst am: 08. Nov 2015 14:14 Titel: TomS Verfasst am: 08. Nov 2015 14:14 Titel: |
 |
|
Ich habe auch nicht behauptet, dass diese Koeffizienten theta direkt den Drehwinkeln (z.B. Eulerwinkeln) um bestimmte Achsen entsprechen. Evtl. hätte ich besser von Koeffizienten statt von Winkeln sprechen sollen.
Grundsätzlich ist dennoch G ein so(3) Element, das einer Drehung U der SO(3) entspricht.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 08. Nov 2015 18:05 Titel: index_razor Verfasst am: 08. Nov 2015 18:05 Titel: |
 |
|
| TomS hat Folgendes geschrieben: | Ich habe auch nicht behauptet, dass diese Koeffizienten theta direkt den Drehwinkeln (z.B. Eulerwinkeln) um bestimmte Achsen entsprechen. Evtl. hätte ich besser von Koeffizienten statt von Winkeln sprechen sollen.
Grundsätzlich ist dennoch G ein so(3) Element, das einer Drehung U der SO(3) entspricht. |
Naja, wenn es sich nicht um Drehwinkel um irgendeine bestimmte Achse handelt, worum handelt es sich dann? Das genau war ja die Frage. Wenn du die Koeffizienten theta als "Drehwinkel" bezeichnest, wirft das im dreidimensionalen die Frage auf, um welche Achse da gedreht wird. Daß du diesen Punkt undefiniert gelassen hast, macht deine Aussage ja noch nicht korrekt, sondern m.E. zunächst mal irreführend.
Worauf ich hinauswollte: Jedem Element der Drehalgebra entspricht ein bestimmter Bivektor, der die Drehebene im Raum aufspannt. Im zweidimensionen gibt es nur eine solche Ebene. Im vierdimensionalen sechs linear unabhängige Ebenen. Im dreidimensionalen gibt es drei. Deswegen gehört zu jedem solchen Bivektor ein dualer Vektor, dessen Richtung die Drehachse und dessen Betrag den Drehwinkel bestimmt. Elemente der Drehalgebra so(3) sind also normale räumliche Vektoren. Das klärt m.E. vollständig die Bedeutung der linearen Struktur der Drehalgebra, nach der ursprünglich gefragt wurde. Die Koeffizienten in Linearkombinationen  solcher Vektoren haben weder direkt noch indirekt irgendwas mit Drehwinkeln in irgendeiner der beteiligten Drehebenen zu tun (allerhöchstens mit den Richungskosinus der Winkel zwischen verschiedenen Drehachsen: solcher Vektoren haben weder direkt noch indirekt irgendwas mit Drehwinkeln in irgendeiner der beteiligten Drehebenen zu tun (allerhöchstens mit den Richungskosinus der Winkel zwischen verschiedenen Drehachsen: ) ). Nur dem Betrag des resultierenden Bivektors (Vektors) entspricht direkt ein Drehwinkel. Darüber sind wir uns sicher einig, ich wollte nur Quantenmechaniker darauf hinweisen und ein mögliches Mißverständnis ausräumen. ). Nur dem Betrag des resultierenden Bivektors (Vektors) entspricht direkt ein Drehwinkel. Darüber sind wir uns sicher einig, ich wollte nur Quantenmechaniker darauf hinweisen und ein mögliches Mißverständnis ausräumen. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18062
|
 TomS Verfasst am: 08. Nov 2015 19:18 Titel: TomS Verfasst am: 08. Nov 2015 19:18 Titel: |
 |
|
| index_razor hat Folgendes geschrieben: | | Naja, wenn es sich nicht um Drehwinkel um irgendeine bestimmte Achse handelt, worum handelt es sich dann? Das genau war ja die Frage. |
Die ursprüngliche Frage war die nach dem Zusammenhang zwischen Liealgebra und Quantenmechanik. Das habe ich im Detail erklärt.
Die Verwendung des Begriffs "Drehwinkel" ist nicht ganz präzise, der Rest passt.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
|
|















