| Autor |
Nachricht |
Gast0011
Gast
|
 Gast0011 Verfasst am: 25. Apr 2015 12:36 Titel: Bell-Zustände unverständliche Notation |
 |
|
Meine Frage:
Guten Tag,
ich habe eine Aufgabe bezüglich reduzierter Dichtematrizen zu lösen, aber verstehe bereits die Notation in der Aufgabenstellung nicht. Vielleicht kann mir ja jemand helfen. Hier die Aufgabe:
Aufgabe:
Gegeben seien die Bell-Zustände
<br />
<br />
\left|B_{01} \right\rangle = \begin{pmatrix} \begin{pmatrix} 0 \\ \frac{1}{\sqrt{2}} \end{pmatrix} \\ \begin{pmatrix} \frac{1}{\sqrt{2}} \\ 0 \end{pmatrix} \\ \end{pmatrix}
<br />
<br />
\left|B_{10} \right\rangle = \begin{pmatrix} \begin{pmatrix} \frac{1}{\sqrt{2}} \\ 0 \end{pmatrix} \\ \begin{pmatrix}0 \\ -\frac{1}{\sqrt{2}} \end{pmatrix} \\ \end{pmatrix}
<br />
<br />
\left|B_{11} \right\rangle = \begin{pmatrix} \begin{pmatrix} 0 \\ \frac{1}{\sqrt{2}} \end{pmatrix} \\ \begin{pmatrix} -\frac{1}{\sqrt{2}} \\ 0 \end{pmatrix} \\ \end{pmatrix}
<br />
)
welches jeweils ein verschränktes System aus Zuständen der Unterräume A und B beschreiben. Die Basis der Unterräume sei so gewählt, dass ^T , \quad \left|-\right\rangle_{A,B} = \left( 0,1 \right)^T )
Zeigen Sie, dass obwohl die Dichtematrizen  für die jeweiligen Zustände unterschiedlich sind, ihre reduzierten Dichtematrizen stets gleich sind.
Ich verstehe allerdings schon nicht, wie man aus der obigen Darstellung im Beispiel von  auf die Dastellung mit Tensorprodukt kommt.
Wäre net wenn mir jemand kurz zeigen/erklären könnte, wie das geht, anstonsten sollte die Aufgabe nicht schwer sein. Danke schon mal.
Meine Ideen:
Ich gehe mal davon aus, dass die Vektoren in der Darstellung der B jeweils die  sein sollen, also
aber auch nach etwas rumprobieren verstehe ich nicht wie man auf die andere Darstllung der Zustände kommt |
|
 |
jh8979
Moderator
Anmeldungsdatum: 10.07.2012
Beiträge: 8582
|
| jh8979 Verfasst am: 25. Apr 2015 12:50 Titel: Re: Bell-Zustände unverständliche Notation |
|
|
| Gast0011 hat Folgendes geschrieben: | Meine Frage:
Ich verstehe allerdings schon nicht, wie man aus der obigen Darstellung im Beispiel von auf die Dastellung mit Tensorprodukt kommt.
|
Es gibt vier verschiedene Basisvektoren im Produktraum:
|+>|+>, |->|+>, |+>|-> und |->|->
Deren Darstellung als Vektor wäre dann
(1,0,0,0), (0,1,0,0) , (0,0,1,0) und (0,0,0,1) |
|
|
Gast0011
Gast
|
| Gast0011 Verfasst am: 25. Apr 2015 13:14 Titel: |
|
|
Hallo, danke erst mal, das hab ich glaube ich auch schon mal bei Wikipedia gesehen. Leider weiß ich immer noch nicht so recht wie ich das jetzt benutzen kann um die Zustände umzuformen.
Mit dem Tensorprodukt habe ich immer so meine Probleme. Könntest du mir evtl. noch einen kleinen Tipp geben? |
|
|
jh8979
Moderator
Anmeldungsdatum: 10.07.2012
Beiträge: 8582
|
| jh8979 Verfasst am: 25. Apr 2015 14:19 Titel: |
|
|
| Gast0011 hat Folgendes geschrieben: | | Hallo, danke erst mal, das hab ich glaube ich auch schon mal bei Wikipedia gesehen. Leider weiß ich immer noch nicht so recht wie ich das jetzt benutzen kann um die Zustände umzuformen. |
Welche Zustände umformen? Du sollst doch Dichtematrizen berechnen. |
|
|
Gast0011
Gast
|
| Gast0011 Verfasst am: 25. Apr 2015 16:11 Titel: |
|
|
Also, ich dachte, ich müsste erst die restlichen Zustände so umformen, wie bei um die Dichtematrizen zu berechnen. Mittlerweile habe ich festgestellt, dass das gar nicht nötig ist. Die Dichtematrizen habe ich also bestimmt. Zum Beispiel:
Ich gehe mal davon aus, dass das jetzt stimmen wird. Sorry manchmal stehe ich etwas auf dem Schlauch  . Danke nochmal.
(Es wäre aber trotdem gut zu wissen, wie man auf die andere Darstellung der B kommt.  ) |
|
|
jh8979
Moderator
Anmeldungsdatum: 10.07.2012
Beiträge: 8582
|
| jh8979 Verfasst am: 25. Apr 2015 16:19 Titel: |
|
|
| Gast0011 hat Folgendes geschrieben: |
(Es wäre aber trotdem gut zu wissen, wie man auf die andere Darstellung der B kommt. ) |
Na, wenn Du z.B. weisst, dass:
Dann lässt sich das doch leicht rauskriegen...
(Ich würde die extra klammern im Vektor mal weglassen, die machen hier nicht so richtig viel Sinn, ich glaub das ist auch was Dich verwirrt.) |
|
|
Gast0011
Gast
|
| Gast0011 Verfasst am: 25. Apr 2015 17:21 Titel: |
|
|
Das verstehe ich jetzt leider auch noch nicht ganz, wenn ich das Produkt der Vektoren bilde, also
gilt dann:
oder wie genau ist das jetzt definiert. Und was hat es dann mit den Indizes A und B auf sich? |
|
|
jh8979
Moderator
Anmeldungsdatum: 10.07.2012
Beiträge: 8582
|
| jh8979 Verfasst am: 25. Apr 2015 17:23 Titel: |
|
|
Viel einfacher:
Du hast vier Basisvektoren im (vierdimensionalen) Produktraum. Bezüglich dieser Basis haben diese Basisvektoren dann natürlich die Darstellungen: (1,0,0,0), (0,1,0,0),... (das gilt für jede Basis)
Du musst also gar nichts rechnen. Das ist einfach der Zustand geschrieben als vierdimensionaler Vektor in einer bestimmten Basis (und nicht mehr als Tenorprodukt geschrieben). |
|
|
Gast0011
Gast
|
| Gast0011 Verfasst am: 25. Apr 2015 18:41 Titel: |
|
|
Also ich habe mir das gerade nochmal auf Wikipedia durchgelesen, dort steht das, wenn
 eine Basis des Vektorraums U ist und  eine Basis des Vektorraums V
dann ist die Basis des Tensorproduktraums  gerade \}) . Das Element dieser Basis wird geschrieben als 
Müsste dann nicht
sein, oder ist mit der Definition von Wikipedia einfach nur gemeint
Ich bekomme nicht zusammen, wieso bei dem Tensorprodukt dann (ohne Rechnung) sonst der Vierervektor mit lediglich einem 1 Element rauskommt. (Außer das es für einen vierdimensionalen, kartesischen Vektorraum intuitiv Sinn macht die Basisvektoren so zu wählen.)
Tut mir leid, vielleicht bin ich heute etwas schwer von Begriff.  |
|
|
jh8979
Moderator
Anmeldungsdatum: 10.07.2012
Beiträge: 8582
|
| jh8979 Verfasst am: 25. Apr 2015 18:56 Titel: |
|
|
Das wäre eine andere Schreibweise (welche irgendwie von den Extraklammern in Deiner Aufgabenstellung impliziert wird, dort aber offensichtlich nicht gemeint ist).
Von vorne: Es gibt einen Basisvektor eines vierdimensionalen Raumes:
Und in dieser Basis ist b_1 der erste Basisvektor, also in Komponentenschreibweise gegeben durch:
 |
|
|
Gast0011
Gast
|
| Gast0011 Verfasst am: 25. Apr 2015 19:29 Titel: |
|
|
Hallo,
also ist das dann jetzt mehr eine Konvention, dass 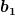 , wenn es der erste Basisvektor ist, genauso aussieht?
Dann müssten jetzt
sein, oder nicht? |
|
|
jh8979
Moderator
Anmeldungsdatum: 10.07.2012
Beiträge: 8582
|
| jh8979 Verfasst am: 25. Apr 2015 19:37 Titel: |
|
|
Das ist korrekt. Das ist aber keine Konvention (zumindest keine ungewöhnliche), das ist die Definition dessen was die Komponentendarstellung meint:
Die Komponenten von a ändern sich natürlich, wenn man eine andere Basis wählt. |
|
|
Gast0011
Gast
|
| Gast0011 Verfasst am: 25. Apr 2015 20:05 Titel: |
|
|
|
Ok, danke dir. Ich werde dann mal versuchen den Rest der Aufgabe damit zu machen. Sollte ich noch fragen haben melde ich wieder. |
|
|
|
Registrieren
Login
FAQ
Suchen
