| Autor |
Nachricht |
Mark97
Gast
|
 Mark97 Verfasst am: 15. Jun 2014 14:01 Titel: Spannung und Frequenz am Transformator |
 |
|
Meine Frage:
Hallo,
ich habe ein Problem mit dem Verständnis des Transformators.
Ich weis natürlich, dass am idealen Transformator das Verhältnis der Spannungen dem Verhältnis der Wicklungen entspricht. Die Sekundärspannung ist somit nur von der Primärspannung sowie dem Wicklungsverhältnis abhängig. Dementsprechend ist sie NICHT abhängig von der Frequenz der Wechselspannung auf der Primärseite (dass dies im realen Transformator durch den Eisenkern nicht ganz der Fall ist ist mir bewusst).
Jetzt gilt jedoch nach Faraday, dass die induzierte Spannung die Ableitung des magnetischen Flusses ist. Der magnetische Fluss müsste direkt proportional zur Primärspannung sein, durch welche er "entsteht". Dementsprechend müsste bei höherer Frequenz der Wechelspannung doch auch die induzierte Spannung auf der Sekundärseite höher sein, da die Ableitung auch größer ist ( sin(wt)' = w*sin(wt) ).
Ich beziehe mich der einfachheit halber auf eine Sinusschwingung, wie es mit anderen Schwingungen aussehen würde, sei dahingestellt.
Meine Ideen:
In der Transformatorenhauptgleichung kommt die Frequenz als Parameter vor, wie ich das erwartet hätte. Möglicherweise habe ich die Anwendung der Transformatorenhauptgleichung jedoch nicht ganz verstanden.
Ich würde mich freuen, wenn mir jemand meinen Gedankenfehler bezüglich der oben dargestellten Überlegung aufzeigen würde und mir vielleicht erklären könnte, wann man die Transformatorenhauptgleichung anwendet.
Grüße
|
|
 |
GvC
Anmeldungsdatum: 07.05.2009
Beiträge: 14861
|
| GvC Verfasst am: 15. Jun 2014 14:25 Titel: |
|
|
| Mark97 hat Folgendes geschrieben: | | Dementsprechend müsste bei höherer Frequenz der Wechelspannung doch auch die induzierte Spannung auf der Sekundärseite höher sein, da die Ableitung auch größer ist ( sin(wt)' = w*sin(wt) ). |
Mal abgesehen von der Unmöglichkeit dessen, was ich fett markiert habe, gilt dasselbe Argument auch auf der Primärseite. Du tust hier so, als sein der Fluss konstant und nur die Frequenz veränderlich. Dann ist die Spannung auf der Primärseite aber um genau denselben Frequenzerhöhungsfaktor erhöht wie die der Sekundärseite.
Normalerweise ist aber die Primärspannung konstant. Bei höherer Frequenz "produziert"*) sie einen um den Frequenzerhöhungsfaktor geringeren Fluss. Die Sekundärspannung bleibt deshalb frequenzunabhängig, solange die Primärspannung frequenzunabhängig ist. In Formeln:
}=N_1\cdot\hat{\Phi}\cdot\omega\cdot\sin{(\omega t)})
Der Scheitelwert lässt sich direkt ablesen zu
Durch die Sekundärspule fließt derselbe Fluss. Also gilt
}=N_2\cdot\hat{\Phi}\cdot\omega\cdot\sin{(\omega t)})
Und damit
*) Die folgende Formulierung wäre besser, aber länger: Der Strom durch die Primärspule stellt sich so ein, dass er einen Fluss erzeugt, der das Induktionsgesetz erfüllt.
|
|
|
Mark97
Gast
|
| Mark97 Verfasst am: 15. Jun 2014 14:39 Titel: |
|
|
Danke für die Antwort und tut mir leid für den Fehler mit der Ableitung des Sinus, sollte natürlich dann ein Kosinus sein..
Wenn ich dich jetzt richtig verstanden habe heißt das, dass mit größerer Frequenz auf der Primärspule der Fluss auch entsprechend kleiner wird. Ist dies nur beim Transformator der Fall, oder sinkt generell bei jeder Spule (die nicht mit einer anderen gekoppelt ist) der Fluss mit steigende Frequenz?
Gruß
|
|
|
GvC
Anmeldungsdatum: 07.05.2009
Beiträge: 14861
|
| GvC Verfasst am: 15. Jun 2014 15:00 Titel: |
|
|
Das gilt allgemein. Auch die Herleitung in meinem vorigen Beitrag bezieht sich ja jeweils nur auf eine Spule.
Im Grunde habe ich mit dem Induktionsgesetz nichts anderes hergeleitet als das ohmsche Gesetz für eine Spule bei Wechselspannung. Ausgehend vom ohmschen Gesetz kommst Du rückwärts natürlich wieder auf das Induktionsgesetz:
oder für die Beträge (Effektivwerte):
Die Induktivität ist definiert als Flussverkettung dividiert durch erregenden Strom, also
Einsetzen
bzw.
|
|
|
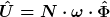
Mark97
Gast
|
| Mark97 Verfasst am: 15. Jun 2014 16:29 Titel: |
|
|
Eine Sache verstehe ich nun aber nicht ganz. Die Induktivität ist ja dementsprechend die Proportionalitätskonstante zwischen magnetischem Fluss und der Stromstärke. Die Induktivität ist doch aber ein fester Wert, der letztlich durch die Bauteilgeometrie bestimmt wird. Wie kann dann der Fluss bei höherer Spannung geringer werden, wenn sich die Induktivität nicht ändert? Oder stehe ich gerade komplett auf dem Schlauch?
Gruß
|
|
|
Mark97
Gast
|
| Mark97 Verfasst am: 15. Jun 2014 16:32 Titel: |
|
|
Tut mir leid für die dumme Frage, ich denke ich habe das jetzt so verstanden. Das heißt also bei höherer Frequenz wird der Strom primärseitig geringer, damit der Fluss ebenfalls geringer wird und das Induktionsgesetz somit erfüllt wird?
Hängt der Strom aber nicht auch vom Übersetzungsverhältnis ab und ist Frequenzunabhängig?
Gruß
|
|
|
GvC
Anmeldungsdatum: 07.05.2009
Beiträge: 14861
|
| GvC Verfasst am: 15. Jun 2014 17:34 Titel: |
|
|
| Mark97 hat Folgendes geschrieben: | Die Induktivität ist ja dementsprechend die Proportionalitätskonstante zwischen magnetischem Fluss und der Stromstärke.
...
Wie kann dann der Fluss bei höherer Spannung geringer werden, wenn sich die Induktivität nicht ändert? |
Da hast Du irgendwie einen falschen Zusammenhang hergestellt. Der Fluss wird nur dann geringer, wenn sich bei konstanter Spannung die Frequenz erhöht. Der Fluss kann auch bei höherer Spannung geringer werden; dann muss die Frequenz nur entsprechend weiter erhöht werden.
| Mark97 hat Folgendes geschrieben: | | Das heißt also bei höherer Frequenz wird der Strom primärseitig geringer, damit der Fluss ebenfalls geringer wird und das Induktionsgesetz somit erfüllt wird? |
Richtig.
| Mark97 hat Folgendes geschrieben: | | Hängt der Strom aber nicht auch vom Übersetzungsverhältnis ab und ist Frequenzunabhängig? |
Bislang haben wir nur über den Magnetisierungsstrom gesprochen. Die in den Spulen eines belasteten Trafos fließenden Ströme sind dagegen im Wesentlichen von der Belastung abhängig. Der Magnetisierungsstrom bleibt bei konstanter Primärspannung und konstanter Frequenz immer derselbe. Der primäre Gesamtstrom setzt sich zusammen aus dem Magnetisierungsstrom und dem über das Windungszahlenverhältnis umgerechneten Sekundärstrom.
Die prinzipielle Funktion eines Trafos ist doch diese:
Bei konstanter Primärspannung kann sich wegen des Induktionsgesetzes der magnetische Fluss nicht ändern. Wenn der Trafo nun aber belastet wird, also ein sekundärseitiger Strom fließt, erzeugt dieser sekundärseitige Strom einen Fluss, der nach Lenzscher Regel dem ursprünglichen Fluss entgegengesetzt ist, der den Fluss also zu schwächen sucht. Da der Fluss aber konstant bleiben muss (sofern die Primärspannung konstant bleibt), muss sich der Primärstrom erhöhen.
Fazit: Der Fluss im Eisenkern eines Trafos hängt nicht vom Primärstrom ab, sondern von der Primärspannung. Damit ist der Fluss nur vom Magnetisierungsstrom abhängig, der im Allgemeinen nur einen ganz kleinen Teil des Primärstromes ausmacht.
|
|
|
Mark97
Gast
|
| Mark97 Verfasst am: 15. Jun 2014 18:32 Titel: |
|
|
Ich denke ich verstehe das ganze nun. Das heißt wenn man bei gegebener Primärspannung die Frequenz erhöht, sinkt damit der primärseitige Magnetisierungsstrom?
Mir stellt sich letztlich jedoch die Frage, wieso nun der Fluss (durch den kleineren Magnetisierungsstrom) sinkt, statt dass sich die sekundäre Spannung erhöhen würde. Welches physikalisch Prinzip sorgt dafür, dass die Sekundärspannung im Verhältnis der Windungen zur Primärspannung steht? Wieso stellt sich der Magnetisierungsstrom und damit auch der Fluss so ein, dass diese Relation erfüllt wird?
| Zitat: | | Bei konstanter Primärspannung kann sich wegen des Induktionsgesetzes der magnetische Fluss nicht ändern. Wenn der Trafo nun aber belastet wird, also ein sekundärseitiger Strom fließt, erzeugt dieser sekundärseitige Strom einen Fluss, der nach Lenzscher Regel dem ursprünglichen Fluss entgegengesetzt ist, der den Fluss also zu schwächen sucht. Da der Fluss aber konstant bleiben muss (sofern die Primärspannung konstant bleibt), muss sich der Primärstrom erhöhen. |
Diesen Teil verstehe ich nicht ganz. Meinst du mit konstanter Primärspannung, dass die Frequenz und Amplitude konstant bleibt? Weil mit einer wirklich konstante Spannung, also Gleichspannung, würde ein Transformator doch garnicht funktionieren, oder?
|
|
|
GvC
Anmeldungsdatum: 07.05.2009
Beiträge: 14861
|
| GvC Verfasst am: 16. Jun 2014 00:06 Titel: |
|
|
| Mark97 hat Folgendes geschrieben: | Welches physikalisch Prinzip sorgt dafür, dass die Sekundärspannung im Verhältnis der Windungen zur Primärspannung steht?
|
Das Induktionsgesetz. Das hatten wir doch weiter oben bereits erörtert.
| Mark97 hat Folgendes geschrieben: | | Wieso stellt sich der Magnetisierungsstrom und damit auch der Fluss so ein, dass diese Relation erfüllt wird? |
Selbe Antwort. Der Magnetisierungsstrom stellt sich gerade so ein, dass das Induktionsgesetz erfüllt ist.
| Mark97 hat Folgendes geschrieben: | | Diesen Teil verstehe ich nicht ganz. Meinst du mit konstanter Primärspannung, dass die Frequenz und Amplitude konstant bleibt? |
Wir reden doch die ganze Zeit von sinusförmiger Wechselspannung, oder? Konstante Wechselspannung bedeutet also Wechselspannung mit konstanter Amplitude. Die Frequenz ist bei den bisherigen Betrachtungen ja gerade nicht konstant. Nach den Auswirkungen bei sich ändernder Frequenz fragst Du doch die ganze Zeit.
|
|
|
Mark97
Gast
|
| Mark97 Verfasst am: 16. Jun 2014 21:17 Titel: |
|
|
Ok vielen Dank, dann habe ich das jetzt so verstanden.
| Zitat: | | Bei konstanter Primärspannung kann sich wegen des Induktionsgesetzes der magnetische Fluss nicht ändern. |
Dies verstehe ich aber noch nicht ganz. Der magnetische Fluss sinkt doch eben, wenn man die Frequenz primärseitig erhöht, oder habe ich das immer noch nicht verstanden? Bei höherer Frequenz nimmt der Blindwiderstandprimärseitig zu, die Stromstärke damit ab und somit wird auch der Fluss kleiner. Oder etwa nicht?
Gruß
|
|
|
PhysikNerd
Gast
|
| PhysikNerd Verfasst am: 24. Dez 2020 18:42 Titel: Nachfrage |
|
|
Hallo GvC,
| GvC hat Folgendes geschrieben: |
Normalerweise ist aber die Primärspannung konstant. Bei höherer Frequenz "produziert"*) sie einen um den Frequenzerhöhungsfaktor geringeren Fluss. Die Sekundärspannung bleibt deshalb frequenzunabhängig, solange die Primärspannung frequenzunabhängig ist.
|
Ich sehe deinen Erklärungsansatz etwas kritisch:
Wie kann es sein, dass bei einer höheren Frequenz sich der magnetische Fluss verkleinert? Dies widerspricht meiner Intuition.
Eine höhere Frequenz von Spannung bedeutet auch eine höhere Frequenz des Magnetisierungsstroms in der Primärspule. Daher ändern sich die magnetischen Wirbelfelder vom Magnetisierungsstrom schneller, die die Querschnittsfläche vom Eisenkern durchstoßen und WÜRDEN einen höheren magnetischen Fluss bewirken, da die Frequenz ja die Änderrungsrate vorgibt.
ABER mit steigender Frequenz wird der Betrag der Stromstärke in der Primärspule (Magnetisierungsstrom) um denselben Faktor kleiner:
Daher wird auch der Scheitelwert des Magnetfelds im Inneren der Spule um denselben Wert kleiner.
Verdoppelt man also die Frequenz:
- verdoppelt sich die Änderungsrate von Stromstärke und Magnetfeld
- halbiert sich der Betrag von Stromstärke und Magnetfeld
Dies sorgt insgesamt dafür, dass der magnetische Fluss sich in der Primärspule nicht mit der Frequenz ändert.
KURZ: Der magnetische Fluss ist frequenzunabhängig, somit ist die Transformation frequenzunabhängig.
Ich würde mich auf eine Rückmeldung freuen, da ich momentan eine Bestätigung brauche 
|
|
|
ML
Anmeldungsdatum: 17.04.2013
Beiträge: 3390
|
| ML Verfasst am: 24. Dez 2020 23:38 Titel: Re: Nachfrage |
|
|
Hallo,
| PhysikNerd hat Folgendes geschrieben: |
Wie kann es sein, dass bei einer höheren Frequenz sich der magnetische Fluss verkleinert? Dies widerspricht meiner Intuition.
|
Die Flussänderung (ausgehend vom Zustand Fluss = 0) ist letztlich das zeitliche Integral über die Primärspannung:
=\Phi_\text{w}(0) + \frac{1}{N} \cdot \int\limits_{0}^t U_\mathrm{i}(\tau)\,\text{d}\tau)
Der Index w steht hier für eine Windung.
Wenn der Sinus zeitlich schneller auf seinen Maximalwert und wieder auf null geht, ist die zugehörige Fläche (das Integral über u) geringer.
| Zitat: |
ABER mit steigender Frequenz wird der Betrag der Stromstärke in der Primärspule (Magnetisierungsstrom) um denselben Faktor kleiner:
|
Was heißt hier "ABER"? Du hast Doch gerade beschrieben, dass der Magnetisierungsstrom (und damit auch die magnetische Flussdichte) mit steigender Frequenz sinkt. Genau das hat GvC doch auch behauptet.
Viele Grüße
Michael
|
|
|
PhysikNerd
Anmeldungsdatum: 24.12.2020
Beiträge: 32
Wohnort: Dortmund
|
| PhysikNerd Verfasst am: 25. Dez 2020 12:50 Titel: Re: Nachfrage |
|
|
Schönen guten Tag,
| ML hat Folgendes geschrieben: |
Die Flussänderung (ausgehend vom Zustand Fluss = 0) ist letztlich das zeitliche Integral über die Primärspannung:
Der Index w steht hier für eine Windung.
Wenn der Sinus zeitlich schneller auf seinen Maximalwert und wieder auf null geht, ist die zugehörige Fläche (das Integral über u) geringer.
|
Das Integral über eine Schwingungsdauer von einer COS - Funktion ist stets 0. Das ist auch sinnvoll, da der magnetische Fluss in der ersten Hälfte der Schwingungsdauer positiv gerichtet und in der anderen Hälfte negativ gerichtet ist.
Dein Beispiel unterstützt meine Annahme, dass die Frequenz überhaupt keinen Einfluss auf den magnetischen Fluss hat, denn:
Betrachtet man nun den magnetischen Fluss der doppelten Frequenz und integriert über seine halbe Schwingungsdauer, dann entspricht das der viertel Periode der einfachen Frequenz. Die Flächen sind in beiden Fällen gleich. Dein Fehler liegt einfach in der Tatsache, dass du über zwei unterschiedliche Zeiten integrierst, da die Schwingungsdauer der beiden Spannungen sich unterscheiden.
| Zitat: |
ABER mit steigender Frequenz wird der Betrag der Stromstärke in der Primärspule (Magnetisierungsstrom) um denselben Faktor kleiner:
|
| ML hat Folgendes geschrieben: |
Was heißt hier "ABER"? Du hast Doch gerade beschrieben, dass der Magnetisierungsstrom (und damit auch die magnetische Flussdichte) mit steigender Frequenz sinkt. Genau das hat GvC doch auch behauptet.
|
Nein, wenn der Betrag der Stromstärke mit steigender Frequenz gleich bleiben würde, dann würde der magnetische Fluss sich sogar erhöhen, da mit der Frequenz seine Änderungsrate steigt. Doch da der Betrag der Stromstärke um denselben Faktor kleiner wird, ändert sich der magnetische Fluss insgesamt nicht.
Um es nun nochmal mit Formeln auszudrücken:
mit
)
Mit der Ableitung ergibt sich:
)
Somit scheint sich der magnetische Fluss zunächst erhöht zu haben. ABER die Stromstärke ist aufgrund des induktiven Widerstands auch frequenzanhängig. Für die Stromstärke in der Spule gilt:
Setzt man die Stromstärke in die obige Formel, so ergibt sich:
)
Die Frequenzen kürzen sich weg, sodass der Betrag des magnetischen Flusses frequenzunabhängig ist:
)
Unabhängig von Formeln: Natürlich DARF der magnetische Fluss NICHT abhängig von der Frequenz sein, sonst würde sich die Ausgangsspannung auch mit der Frequenz ändern, was ja bei einem Transformator eben nicht der Fall ist.
Viele Grüße,
Yakup
|
|
|
ML
Anmeldungsdatum: 17.04.2013
Beiträge: 3390
|
| ML Verfasst am: 25. Dez 2020 18:53 Titel: Re: Nachfrage |
|
|
Hallo,
| Zitat: |
Dein Beispiel unterstützt meine Annahme, dass die Frequenz überhaupt keinen Einfluss auf den magnetischen Fluss hat, denn:
|
Wenn Du die Spannung =U_0 \cdot \sin(\omega t)) bei einer Spule über eine halbe Periode integrierst (beispielwsweise von 0...T/2), so erhältst Du das Doppelte des maximalen magnetischen Flusses, der in dem Transformator auftritt. In diesem Zeitbereich verändert sich die Flussdichte von ihrem Minimalwert (negative Amplitude) zu ihrem Maximalwert (positive Amplitude).
Wenn das Integral groß ist, ist auch der maximale Fluss groß. Wenn es klein ist, beispielsweise weil die Periodendauer klein ist, ist auch der maximale Fluss klein.
| Zitat: |
Dein Fehler liegt einfach in der Tatsache, dass du über zwei unterschiedliche Zeiten integrierst, da die Schwingungsdauer der beiden Spannungen sich unterscheiden.
|
Genau. Die Schwingungsdauern unterscheiden sich. Darum geht es gerade.
| Zitat: |
Nein, wenn der Betrag der Stromstärke mit steigender Frequenz gleich bleiben würde, dann würde der magnetische Fluss sich sogar erhöhen, da mit der Frequenz seine Änderungsrate steigt.
|
Auf welchem physikalischen Gesetz basiert Deine Behauptung?
Viele Grüße
Michael
|
|
|
PhysikNerd
Anmeldungsdatum: 24.12.2020
Beiträge: 32
Wohnort: Dortmund
|
| PhysikNerd Verfasst am: 25. Dez 2020 20:15 Titel: Re: Nachfrage |
|
|
| ML hat Folgendes geschrieben: |
Auf welchem physikalischen Gesetz basiert Deine Behauptung?
|
Ich hatte meinen Beitrag oben editiert. Die Rechnung findet sich dort ☺️
Lg
|
|
|
ML
Anmeldungsdatum: 17.04.2013
Beiträge: 3390
|
| ML Verfasst am: 25. Dez 2020 21:52 Titel: Re: Nachfrage |
|
|
Hallo,
| PhysikNerd hat Folgendes geschrieben: | | ML hat Folgendes geschrieben: |
Auf welchem physikalischen Gesetz basiert Deine Behauptung?
|
Ich hatte meinen Beitrag oben editiert. Die Rechnung findet sich dort ☺️
|
Ja, ich hab's gesehen. Du vermischst dort die Rechnung im Zeitbereich mit den reellwertigen zeitabhängigen Größen , i(t), \phi(t)) mit der Rechnung im Frequenzbereich mit den komplexwertigen Wechselstromgrößen , \underline I(j\omega), \underline \phi(j\omega)) . Der Fehler ist so grob, dass jede weitere Analyse im Detail Zeitverschwendung ist.
| Zitat: |
Unabhängig von Formeln: Natürlich DARF der magnetische Fluss NICHT abhängig von der Frequenz sein, sonst würde sich die Ausgangsspannung auch mit der Frequenz ändern, was ja bei einem Transformator eben nicht der Fall ist. |
Wir das mal Schritt für Schritt.
Wir geben für eine Spule/einen unbelasteten Transformator die Spannung vor:
 = U_0 \cdot \cos(2 \pi f t))
Nach dem Induktionsgesetz gilt dann bei einer Windungszahl von N:
=\Phi_0 + \frac{1}{N} \int \limits_0^t u(t) \mathrm{d}t = \Phi_0 + \frac{U_0}{N \cdot 2 \pi f} \cdot \sin(2 \pi f t))
Zur Darstellung wählen wir  .
Und jetzt gibst Du die zweite Formel bitte mal für ein festes  und ein festes  in ein Programm ein, das Formeln darstellen kann (z. B. Geogebra, Wolfram Alpha, Matlab o. ä.)
Zunächst wählst Du die Frequenz 10 Hz, dann 100 Hz und dann 1000 Hz. Berichte mir nachher mal, ob sich die Amplitude des Flusses verändert oder nicht.
Und danach können wir uns darüber unterhalten, WESHALB der Fluss bei gegebener Spannung von der Frequenz abhängt und nicht, OB das überhaupt der Fall ist.
Ich unterhalte mich doch auch nicht darüber, ob ein Apfel auf den Boden fällt, wenn man ihn loslässt, sondern nur darüber, wie man das beschreiben kann.
Viele Grüße
Michael
|
|
|
PhysikNerd
Anmeldungsdatum: 24.12.2020
Beiträge: 32
Wohnort: Dortmund
|
|
|
ML
Anmeldungsdatum: 17.04.2013
Beiträge: 3390
|
| ML Verfasst am: 26. Dez 2020 03:26 Titel: |
|
|
Hallo,
| PhysikNerd hat Folgendes geschrieben: |
Ich betrachte nun als Beispiel zwei sinusförmige Spannungen, einmal mit einfacher Frequenz und einmal mit doppelter Frequenz und integriere diese über eine gemeinsame Zeit:
|
"Gemeinsame Zeit" ist das Problem.
| Zitat: |
Falls du es mir immer noch nicht glauben möchtest, habe ich dir zusätzlich eine Skizze der beiden Flächen als Anhang hinzugefügt. Schau dir die beiden Skizzen an und sag mir, ob sich die beiden Flächen unterscheiden.
|
Die von Dir gezeichneten Flächen sind nicht relevant.
Du musst jeweils so lange integrieren wie der Fluss noch steigt, d. h. jeweils eine komplette positive Halbwelle des Sinus. Bei einer hohen Frequenz musst Du dann wenig Fläche integrieren und bei einer niedrigen Frequenz hast Du viel Fläche.
Nur so bekomst Du heraus, wie groß der Unterschied zwischen dem größten und dem kleinsten (d. h. dem betragsmäßig größten negativen) Fluss im Kern ist?
Viele Grüße
Michael
|
|
|
PhysikNerd
Anmeldungsdatum: 24.12.2020
Beiträge: 32
Wohnort: Dortmund
|
| PhysikNerd Verfasst am: 26. Dez 2020 21:30 Titel: |
|
|
Hallo Michael,
| ML hat Folgendes geschrieben: |
Du musst jeweils so lange integrieren wie der Fluss noch steigt, d. h. jeweils eine komplette positive Halbwelle des Sinus. Bei einer hohen Frequenz musst Du dann wenig Fläche integrieren und bei einer niedrigen Frequenz hast Du viel Fläche.
Nur so bekomst Du heraus, wie groß der Unterschied zwischen dem größten und dem kleinsten (d. h. dem betragsmäßig größten negativen) Fluss im Kern ist?
|
Okay, so macht es Sinn. Sorry!
Wir wollen ja den maximalen Fluss berechnen, daher muss ich solange integrieren, bis der Scheitelwert des magnetischen Flusses erreicht wird.
Ich habe es auch online geplottet: Bei doppelter Frequenz, halbiert sich der magnetische Fluss.
Das erstaunt mich sehr, da die ganzen vorherigen Gedanken von mir somit komplett ungültig sind..
Wenn man den magnetischen Fluss über das Magnetfeld berechnet, so muss man wahrscheinlich damit argumentieren, dass sich aufgrund des induktiven Widerstands die Stromstärke und mit diesem auch der Betrag des Magnetfelds verkleinert.
Gleichzeitig hatte ich den Gedankengang, dass bei einer höheren Frequenz sich ja auch die Steigung  vergrößert. Somit müsste sich der magnetische Fluss schneller ändern. Ich weiß nur nicht, was an dem Gedanken falsch ist.
Vielen Dank für deine Zeit !
|
|
|
PhysikNerd
Anmeldungsdatum: 24.12.2020
Beiträge: 32
Wohnort: Dortmund
|
| PhysikNerd Verfasst am: 30. Dez 2020 21:20 Titel: |
|
|
Ich habe nun das Rätsel gelöst.
Du sprichst von dem magnetischen Fluss 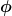 , während ich die ganze Zeit von der Änderungsrate vom magnetischen Fluss  gesprochen habe.
Verdoppelt man die Frequenz der Wechselspannung, so halbiert sich der magnetische Fluss 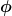zwar, aber die Änderungsrate bleibt konstant, da wir bei der doppelten Frequenz lediglich die Hälfte der Zeit in Betracht gezogen haben (siehe Integral). Man dividiert hier also die Hälfte des magnetischen Flusses mit der Hälfte der Zeit.
Doch auch wenn der magnetische Fluss in der Primärspule mit steigender Frequenz sinkt, hat dies keinen Einfluss auf die Transformatorgleichung. Man betrachtet hier nämlich NICHT den magnetischen Fluss sondern die Änderung des magnetischen Flusses durch eine einzelne Windung  . In Formeln gefasst:
Auf der Primärseite gilt:
Auf der Sekundärseite gilt:
Setzt man die beiden Gleichungen gleich, so kommt man insgesamt wieder auf die gewöhnliche Transformatorgleichung:
|
|
|
ML
Anmeldungsdatum: 17.04.2013
Beiträge: 3390
|
| ML Verfasst am: 31. Dez 2020 02:33 Titel: |
|
|
Hallo,
| PhysikNerd hat Folgendes geschrieben: | | Ich habe nun das Rätsel gelöst. |
Das freut mich!
| Zitat: |
Du sprichst von dem magnetischen Fluss 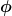, während ich die ganze Zeit von der Änderungsrate vom magnetischen Fluss gesprochen habe.
|
Jetzt seh ich es auch. Immerzu hast Du von der Änderungsrate des magnetischen Flusses gesprochen. Und immerzu habe ich es überlesen. Das geht mir jetzt noch manchmal so! 
| PhysikNerd hat Folgendes geschrieben: |
Wie kann es sein, dass bei einer höheren Frequenz sich der magnetische Fluss verkleinert? Dies widerspricht meiner Intuition. |
| PhysikNerd hat Folgendes geschrieben: |
KURZ: Der magnetische Fluss ist frequenzunabhängig, somit ist die Transformation frequenzunabhängig.
|
| PhysikNerd hat Folgendes geschrieben: |
Dein Beispiel unterstützt meine Annahme, dass die Frequenz überhaupt keinen Einfluss auf den magnetischen Fluss hat, denn:
|
| PhysikNerd hat Folgendes geschrieben: |
Unabhängig von Formeln: Natürlich DARF der magnetische Fluss NICHT abhängig von der Frequenz sein, sonst würde sich die Ausgangsspannung auch mit der Frequenz ändern, was ja bei einem Transformator eben nicht der Fall ist.
|
| PhysikNerd hat Folgendes geschrieben: |
Bei doppelter Frequenz ist der magnetische Fluss genau derselbe wie bei einfacher Frequenz.
|
| PhysikNerd hat Folgendes geschrieben: |
Wir wollen ja den maximalen Fluss berechnen, daher muss ich solange integrieren, bis der Scheitelwert des magnetischen Flusses erreicht wird.
|
Viele Grüße
Michael
|
|
|
PhysikNerd
Anmeldungsdatum: 24.12.2020
Beiträge: 32
Wohnort: Dortmund
|
| PhysikNerd Verfasst am: 31. Dez 2020 02:59 Titel: |
|
|
Hi Michael, das sollte auch überhaupt gar kein Vorwurf an dich sein. Es ist ganz klar mein Fehler, da ich mich schlicht und einfach falsch ausgedrückt habe.
Ich habe die ganze Zeit die „Änderungsrate vom magnetischen Fluss“ gemeint und habe blöderweise aber immer nur vom „magnetischen Fluss“ gesprochen. Meine Rechnung zeigte ja die Änderungsrate, die konstant bleibt:
| PhysikNerd hat Folgendes geschrieben: |
Um es nun nochmal mit Formeln auszudrücken:
mit
Mit der Ableitung ergibt sich:
Somit scheint sich der magnetische Fluss zunächst erhöht zu haben. ABER die Stromstärke ist aufgrund des induktiven Widerstands auch frequenzanhängig. Für die Stromstärke in der Spule gilt:
Setzt man die Stromstärke in die obige Formel, so ergibt sich:
Die Frequenzen kürzen sich weg, sodass der Betrag des magnetischen Flusses frequenzunabhängig ist:
Unabhängig von Formeln: Natürlich DARF der magnetische Fluss NICHT abhängig von der Frequenz sein, sonst würde sich die Ausgangsspannung auch mit der Frequenz ändern, was ja bei einem Transformator eben nicht der Fall ist.
|
Deswegen hatte ich immer wieder darauf bestanden, den magnetischen Fluss über die gemeinsame Zeit zu integrieren, da sonst die Zeit in der Änderungsrate unterschiedlich wäre:
| PhysikNerd hat Folgendes geschrieben: |
Betrachtet man nun den magnetischen Fluss der doppelten Frequenz und integriert über seine halbe Schwingungsdauer, dann entspricht das der viertel Periode der einfachen Frequenz. Die Flächen sind in beiden Fällen gleich. Dein Fehler liegt einfach in der Tatsache, dass du über zwei unterschiedliche Zeiten integrierst, da die Schwingungsdauer der beiden Spannungen sich unterscheiden.
|
Naja, echt blöd 😂 Jetzt haben wir das Problem gelöst, vielen lieben Dank dafür ☺️
|
|
|
ML
Anmeldungsdatum: 17.04.2013
Beiträge: 3390
|
| ML Verfasst am: 31. Dez 2020 03:53 Titel: |
|
|
Hehe,
| PhysikNerd hat Folgendes geschrieben: | | Hi Michael, das sollte auch überhaupt gar kein Vorwurf an dich sein. Es ist ganz klar mein Fehler, da ich mich schlicht und einfach falsch ausgedrückt habe. |
Keine Sorge, habe Dich nur ein wenig aufgezogen
Viele Grüße
Michael
|
|
|
|
|
Registrieren
Login
FAQ
Suchen
