| Autor |
Nachricht |
Margarita90
Anmeldungsdatum: 30.11.2009
Beiträge: 61
|
 Margarita90 Verfasst am: 13. Feb 2014 18:48 Titel: Existenz Bewegungsintegral Margarita90 Verfasst am: 13. Feb 2014 18:48 Titel: Existenz Bewegungsintegral |
 |
|
Hey,
ich fang mal ganz allgemein an:
Gibt es eigentlich für jedes Anfangswertproblem ein Integral of Motion / Bewegungsintegral?
Liebe Grüße! |
|
 |
jumi
Gast
|
 jumi Verfasst am: 13. Feb 2014 18:54 Titel: jumi Verfasst am: 13. Feb 2014 18:54 Titel: |
 |
|
Nein!
Es gibt auch Anfangswertprobleme, die nichts mit Motion oder Bewegungsintegralen zu tun haben. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18062
|
 TomS Verfasst am: 13. Feb 2014 19:16 Titel: Re: Existenz Bewegungsintegral TomS Verfasst am: 13. Feb 2014 19:16 Titel: Re: Existenz Bewegungsintegral |
 |
|
| Margarita90 hat Folgendes geschrieben: | | Gibt es eigentlich für jedes Anfangswertproblem ein Integral of Motion / Bewegungsintegral? |
Ein Bewegungsintegral hat doch nichts mit einer Anfangsbedingung zu tun.
Kennst du den Lagrangeformalismus und das Noethertheorem?
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Margarita90
Anmeldungsdatum: 30.11.2009
Beiträge: 61
|
 Margarita90 Verfasst am: 13. Feb 2014 20:36 Titel: Margarita90 Verfasst am: 13. Feb 2014 20:36 Titel: |
 |
|
Hm, naja in meinem Fall schon irgendwie...
Ich habe das AWP
 \\
<br />
\dot x_2=x_1 x_2\\
<br />
x_1(0),x_2(0) \in M=\lbrace (x_1,x_2) \in \mathbb{R}^2:x_2>0\rbrace)
gegeben und soll dafür ein Bewegungsintegral finden.
Auf "gut Glück" hat es bisher nicht geklappt. Habt ihr eine Idee?
Liebe Grüße! |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18062
|
 TomS Verfasst am: 13. Feb 2014 23:09 Titel: TomS Verfasst am: 13. Feb 2014 23:09 Titel: |
 |
|
Das Bewegungsintegral findest du systematisch, indem du auf die Lagrangefunktion das Noethertheorem anwendest.
Also solltest du zuerst die Lagrangefunktion konstruieren, aus der diese Bewegungsgleichungen folgen. Anschließend ermittelst du die Symmetrien und daraus letztlich die Erhaltungsgrößen.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18062
|
 TomS Verfasst am: 14. Feb 2014 06:45 Titel: TomS Verfasst am: 14. Feb 2014 06:45 Titel: |
 |
|
Eine ander Frage: deineBewegungsgleichungen sind sicher von erster Ordnung, d.h. es kommen nur die Geschwindigkeiten, nicht die Beschleunigungen vor??
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Margarita90
Anmeldungsdatum: 30.11.2009
Beiträge: 61
|
 Margarita90 Verfasst am: 14. Feb 2014 08:56 Titel: Margarita90 Verfasst am: 14. Feb 2014 08:56 Titel: |
 |
|
| TomS hat Folgendes geschrieben: | | Eine ander Frage: deineBewegungsgleichungen sind sicher von erster Ordnung? |
Ja, ich denke schon.
Dann probier ich den oben beschriebenen Weg mal... |
|
 |
Margarita90
Anmeldungsdatum: 30.11.2009
Beiträge: 61
|
 Margarita90 Verfasst am: 14. Feb 2014 10:39 Titel: Margarita90 Verfasst am: 14. Feb 2014 10:39 Titel: |
 |
|
Ich weiß nicht, wie ich auf die Lagrangefunktion kommen soll...
Ich bin jetzt davon ausgegangen, dass sich die erste Gleichung von
 kommt, also kommt, also
) . .
Entstand die zweite Gleichung aus
 kommt man auf kommt man auf

Diese beiden Funktionen  kann ich jetzt nicht zu dem gesuchten kann ich jetzt nicht zu dem gesuchten 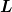 zusammenführen, ohne dass sie sich "gegenseitig behindern". Die Ableitungen gehen dann also nicht mehr auf. Ich weiß auch nicht, wie ich das reparieren kann. Natürlich könnte noch ein komplizierteres System dahinterstecken, aber darauf komme ich nicht zusammenführen, ohne dass sie sich "gegenseitig behindern". Die Ableitungen gehen dann also nicht mehr auf. Ich weiß auch nicht, wie ich das reparieren kann. Natürlich könnte noch ein komplizierteres System dahinterstecken, aber darauf komme ich nicht 
Kann mir noch jemand helfen, bitte! |
|
 |
Huggy
Anmeldungsdatum: 16.08.2012
Beiträge: 785
|
 Huggy Verfasst am: 14. Feb 2014 12:44 Titel: Huggy Verfasst am: 14. Feb 2014 12:44 Titel: |
 |
|
Kurz und schmerzlos: Mit  ergibt sich ergibt sich
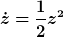
Man hat also das komplexe Bewegungsintegral
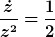
Daraus ergeben sich die reellen Bewegungsintegrale
= \frac {1}{2})
= 0)
Edit: Man könnte bei dem gegebenen DGL-System auch gleich durch die rechten Seiten teilen und hat dann ohne Umweg über das Komplexe 2 Bewegungsintegrale dastehen. |
|
 |
Margarita90
Anmeldungsdatum: 30.11.2009
Beiträge: 61
|
 Margarita90 Verfasst am: 15. Feb 2014 13:29 Titel: Margarita90 Verfasst am: 15. Feb 2014 13:29 Titel: |
 |
|
Hallo Huggy,
ich weiß leider gar nicht, was du da gemacht hast. Also was du gerechnet hast schon, aber nicht, warum.
Du hast es auf eine 1-dim DGL reduziert. Aber wieso bildest du Real- und Imaginärteil?
Ein Bewegungsintegral soll bei meiner Aufgabe eine Abb. ) sein, deren zeitliche Ableitung verschwindet. Das trifft zwar auf sein, deren zeitliche Ableitung verschwindet. Das trifft zwar auf 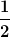 auch zu, aber das ist ja unabhängig vom DGL-System... auch zu, aber das ist ja unabhängig vom DGL-System... |
|
 |
Huggy
Anmeldungsdatum: 16.08.2012
Beiträge: 785
|
 Huggy Verfasst am: 15. Feb 2014 15:41 Titel: Huggy Verfasst am: 15. Feb 2014 15:41 Titel: |
 |
|
Was ist bei dieser Aufgabenstellung mit Bewegungsintegral gemeint?
Mir ist der Begriff Bewegungsintegral im Zusammenhang mit den üblichen Bewegungsgleichungen physikalischer Systeme bekannt. Das sind Differentialgleichungen 2. Ordnung. Als Bewegungsintegrale bezeichnet man dort zeitlich konstante Funktionen der Ortskoordinaten und deren ersten Ableitungen, den Geschwindigkeiten. Beispiel: die Gesamtenergie eines Systems.
Hier beginnt man schon mit einem DGL-System 1. Ordnung. Das lässt sich immer so umschreiben, dass auf einer Seite nur Konstanten stehen, siehe das Edit zu meiner vorigen Antwort. Es macht hier also wenig Sinn, eine zeitlich konstante Funktion der Variablen und ihrer ersten Ableitungen als Bewegungsintegral zu bezeichnen. Aber auf diese Interpretation bezieht sich meine Antwort.
Du bezeichnest jetzt eine zeitlich konstante Funktion lediglich der Variablen als Bewegungsintegral. Dann wäre Bewegungsintegral eine andere Bezeichnung für die Bahnkurve. Diese bekommt man, indem man aus den Lösungen , x_2(t)}) des DGL-Systems die Zeit eliminiert. Die Bahnkurve lässt sich in der Form des DGL-Systems die Zeit eliminiert. Die Bahnkurve lässt sich in der Form =0) darstellen. darstellen.
Was also ist hier mit Bewegungsintegral gemeint? |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18062
|
 TomS Verfasst am: 15. Feb 2014 15:55 Titel: TomS Verfasst am: 15. Feb 2014 15:55 Titel: |
 |
|
@Huggy: deine Lösung ist sehr elegant - Lösen durch hinschauen; ich habe dagegen echt Probleme, eine Lagrangefunktion zu finden, die die Bewegungsgleichungen reproduziert; und eine Symetrietrnsformation fehlt mir dann auch noch; hast du dir das mal angeschaut?
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Huggy
Anmeldungsdatum: 16.08.2012
Beiträge: 785
|
 Huggy Verfasst am: 15. Feb 2014 19:41 Titel: Huggy Verfasst am: 15. Feb 2014 19:41 Titel: |
 |
|
| TomS hat Folgendes geschrieben: | | @Huggy: deine Lösung ist sehr elegant - Lösen durch hinschauen; ich habe dagegen echt Probleme, eine Lagrangefunktion zu finden, die die Bewegungsgleichungen reproduziert; und eine Symetrietrnsformation fehlt mir dann auch noch; hast du dir das mal angeschaut? |
Das habe ich nicht probiert und da fehlt mir auch eine Idee. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18062
|
 TomS Verfasst am: 15. Feb 2014 19:51 Titel: TomS Verfasst am: 15. Feb 2014 19:51 Titel: |
 |
|
| Huggy hat Folgendes geschrieben: | | Das habe ich nicht probiert und da fehlt mir auch eine Idee. |
Was funktioniert denn bei dir nicht?
Ich hab' zunächst L als bilinear in den Orten und Geschwindigkeiten angenommen. Dann bekomme ich die Terme erster Ordung hin, aber im Potential passen nie alle Vorzeichen.
Dann hab' ich versucht, das Gleichungssystem als Hamiltonsche Bewegungsgleichungen in x und p zu interpretieren; wieder funktioniert das nicht mit allen Vorzeichen (oder ich verrechne mich immer an der selben Stelle)
Anyway - das Potential sähe sowieso komisch aus, eine Symmetrie kann ich mir da kaum vorstellen. Die Erhaltungsgröße die du konstruiert hast sieht auch irgendwie merkwürdig aus. Wahrscheinlich muss man irgendeine (einfache) nichtlineare Koordinatentransformation raten, dann passt wieder alles.
@Margarita90: hast du irgendeinen gemeinsamen Vorfaktor gekürzt, oder sind das wirklich die originalen Bewegungsgleichungen? Wie lautet denn die originale Aufgabe?
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Huggy
Anmeldungsdatum: 16.08.2012
Beiträge: 785
|
 Huggy Verfasst am: 16. Feb 2014 09:12 Titel: Huggy Verfasst am: 16. Feb 2014 09:12 Titel: |
 |
|
| TomS hat Folgendes geschrieben: | | Was funktioniert denn bei dir nicht? |
Da ich gar keinen Versuch in diese Richtung unternommen hatte, konnte weder etwas funktionieren noch nicht funktionieren.
Bildet man  und eliminiert daraus die ersten Ableitungen mittels der gegebenen Gleichungen, sieht man jedenfalls, dass diese Bewegungsgleichungen nicht durch ein konservatives Kraftfeld erzeugt werden können. und eliminiert daraus die ersten Ableitungen mittels der gegebenen Gleichungen, sieht man jedenfalls, dass diese Bewegungsgleichungen nicht durch ein konservatives Kraftfeld erzeugt werden können. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18062
|
 TomS Verfasst am: 16. Feb 2014 15:23 Titel: TomS Verfasst am: 16. Feb 2014 15:23 Titel: |
 |
|
| Huggy hat Folgendes geschrieben: | bildet man  und eliminiert daraus die ersten Ableitungen mittels der gegebenen Gleichungen, sieht man jedenfalls, dass diese Bewegungsgleichungen nicht durch ein konservatives Kraftfeld erzeugt werden können. und eliminiert daraus die ersten Ableitungen mittels der gegebenen Gleichungen, sieht man jedenfalls, dass diese Bewegungsgleichungen nicht durch ein konservatives Kraftfeld erzeugt werden können. |
Lass' uns das mal weiterverfolgen (auf die Idee bin ich noch nicht gekommen, ich habe direkt mit den ersten Ableitungen gearbeitet)
Du setzt
)

Dann berechnest du (bitte prüfen, ob Rechenfehler)
)
)
Das wären jetzt ganz gewöhnliche Euler-Lagrange-Gleichungen, für die eine Lagrangefunktion der Form L=T-V zu konstruieren ist. Versuchen wir's mit einem Potenzansatz
 = ax^4 + bx^3y + cx^2y^2 + dxy^3 + ey^4)
Wenn ich nun die rechten Seiten der Bewegungleichungen daraus ableiten will, also
}{\partial x,y})
berechnen, dann lande ich mittels Koeffizientenvergleich bei


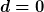

und
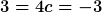
Ist es das, was du meinst?
Ja, egal welchen Ansatz ich wähle - Lagrangefunktion linear in den Geschwindigkeiten, Lagrangefunktion quadratisch in den Geschwindigkeiten, Hamiltonfunktion in (x,y) d.h. y entspr. kan. konj. Impuls - es geht immer eine Gleichung um ein Vorzeichen nicht auf. D.h. ich finde kein L oder H, das die Gleichungen reproduzieren kann.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18062
|
 TomS Verfasst am: 16. Feb 2014 16:15 Titel: TomS Verfasst am: 16. Feb 2014 16:15 Titel: |
 |
|
Ich hab jetzt nochmal versucht, das System als Hamiltonsches Gleichungssystem zu interpretieren. Egal ob ich x oder y dann mit p identifiziere, ich muss immer ein Vorzeichen in
)
in der ersten Gleichung umdrehen, sonst passt das nicht.
Dann nochetwas: ich habe festgestellt, dass man deinen Ansatz mit z=x+iy benutzen kann, um nach einer komplexen Transformation

die Bewegungleichung

abzuleiten. Das wäre ein freies Teilchen, allerdings nicht mit beliebiger sondern fester Geschwindigkeit

Ich kann es nicht beweisen, aber ich bezweifle, dass es sich um ein korrektes Lagrangesches System handelt. Und beim Hamiltonschen System habe ich auch meine Zweifel.
Die ursprüngliche und vollständige Aufgabenstellung wäre interessant.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18062
|
 TomS Verfasst am: 16. Feb 2014 17:29 Titel: TomS Verfasst am: 16. Feb 2014 17:29 Titel: |
 |
|
So, jetzt hab ich alles zusammen. Es handelt sich um ein freies Teilchen in der komplexen w-Ebene. Die Lagrangefunktion lautet
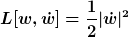
Die Bewegungsgleichungen lauten

Die Erhaltungsgröße entspricht gerade dem Impuls, also

Nun kann man eine komplexe Funktion z(w) der Form

einführen und das Problem in dieser neuen Funktion z formulieren. Dann ist

Die Lagrangefunktion in z lautet dann

Da es sich um ein freies Teilchen handelt ist dies auch gleich der erhaltenen Gesamtenergie

Daneben kann man mit w = u+iv auch den Drehimpuls umformulieren
)
Den Ausdruck für J[z] spare ich mir.
Was jetzt noch fehlt sind die Symmetrien von L[w] sowie L[z], um das Noether-Theorem anwenden zu können. Im Falle von L[w] ist das trivial, es handelt sich einfach um die Translationsinvarianz

sowie die Rotationsinvarianz

Um deren Entsprechung in z zu finden, muss man sich nur überlegen, was die Funktion z(w) in der komplexen Ebene bewirkt und wie sie Geraden sowoe Kreise um den Ursprung abbildet.
Ich habe noch nicht verifiziert, dass die o.g. Lagrangefunktion L[z] die korrekten Bewegungsgleichungen liefert. Der Ansatz dafür lautet

Analog für z*.
Dafür muss man die Lagrangefunktion als

in den unabhängigen Variablen z und z* auffassen.
Wichtig: die ursprünglichen Gleichungen waren m.E. nicht die allgemeinen Bewegunggleichungen, sondern bereits die Gleichungen für einen speziellen Wert

also ein spezielles Anfangswertproblem.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Margarita90
Anmeldungsdatum: 30.11.2009
Beiträge: 61
|
 Margarita90 Verfasst am: 16. Feb 2014 18:36 Titel: Margarita90 Verfasst am: 16. Feb 2014 18:36 Titel: |
 |
|
Hallo ihr beiden,
ich habe an der Aufgabenstellung tatsächlich nichts verändert.
Gegeben ist die Menge 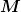 , die ich schon erwähnt hatte, das AWP mit den Anfangswerten , die ich schon erwähnt hatte, das AWP mit den Anfangswerten ,x_2(0) \in M) und Aufgabenteil 1 heißt (original): und Aufgabenteil 1 heißt (original):
Find an integral of motion.
Hinterher ist noch der Fluss zu bestimmen und das Phasenportait zu skizzieren.
Liebe Grüße |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18062
|
 TomS Verfasst am: 16. Feb 2014 18:40 Titel: TomS Verfasst am: 16. Feb 2014 18:40 Titel: |
 |
|
OK, danke ...
... hoffe, meine Ideen helfen weiter
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Huggy
Anmeldungsdatum: 16.08.2012
Beiträge: 785
|
 Huggy Verfasst am: 17. Feb 2014 11:11 Titel: Huggy Verfasst am: 17. Feb 2014 11:11 Titel: |
 |
|
@TomS
| TomS hat Folgendes geschrieben: |
)
)
Das wären jetzt ganz gewöhnliche Euler-Lagrange-Gleichungen, für die eine Lagrangefunktion der Form L=T-V zu konstruieren ist. |
Das kam bei mir auch heraus. Auf der rechten Seite stehen bis auf den Massefaktor die Kraftkomponenten 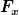 und und 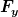 . Leitet man nun . Leitet man nun 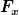 nach y und nach y und 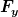 nach x ab, sieht man, dass diese Ableitungen nicht gleich sind. Die für die Existenz eines Potentials erforderliche Integrabilitätsbedingung ist also nicht erfüllt. nach x ab, sieht man, dass diese Ableitungen nicht gleich sind. Die für die Existenz eines Potentials erforderliche Integrabilitätsbedingung ist also nicht erfüllt.
@Margarita90
| Margarita90 hat Folgendes geschrieben: | Aufgabenteil 1 heißt (original):
Find an integral of motion. |
Leider hast du immer noch nicht beantwortet, wie ihr in der Vorlesung "integral of motion" definiert habt. Im Moment neige ich zu der Vermutung, dass damit nicht das Bewegungsintegral im physikalischen Sinne gemeint ist, sondern eine Größe, die mir in der Mathematik in der Theorie der exakten Differentialgleichungen in der deutschsprachigen Literatur als "Erstes Integral" der DGL in trüber Erinnerung ist. Das folgende bezieht sich auf diese Vermutung.
Aus den Ausgangsgleichungen ergibt sich für die Trajektorien (Bahnkurven) die DGL

oder anders geschrieben
 \mathrm dy =0)
 \mathrm dx + B(x,y) \mathrm dy =0)
Wegen  ist diese DGL nicht exakt. Das ist die Aussage, zu den Bewegungsgleichungen existiert kein Potential, in anderer Form. Nun kann man versuchen, einen integrierenden Faktor ist diese DGL nicht exakt. Das ist die Aussage, zu den Bewegungsgleichungen existiert kein Potential, in anderer Form. Nun kann man versuchen, einen integrierenden Faktor ) zu finden, mit dem die DGL zu finden, mit dem die DGL
M(x,y) \mathrm dx + B(x,y)M(x,y) \mathrm dy =0)
exakt wird. Im allgemeinen ist das recht schwierig. Einfacher ist es, falls es einen integrierenden Faktor gibt, der nur von x oder nur von y abhängt. Da
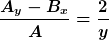
nur von y abhängt, gibt es einen nur von y abhängenden integrierenden Faktor. Man erhält ihn aus der DGL
)
Das führt zu

Man sollte allerdings meine Rechnungen noch mal prüfen. Nach Multiplikation mit M lautet die DGL für die Trajektorien
\mathrm dy =0)
Es ist jetzt eine Funktion G(x,y) zu finden, die

erfüllt. Man erhält:

Dieses G wird nun, wenn mich meine Erinnerung nicht trügt, als ein "Erstes Integral" der DGL bezeichnet. Auf den Trajektorien der DGL ist G konstant. Das würde zu einer englischen Bezeichnung "integral of motion" oder "constant of motion" passen. |
|
 |
Margarita90
Anmeldungsdatum: 30.11.2009
Beiträge: 61
|
 Margarita90 Verfasst am: 17. Feb 2014 15:20 Titel: Margarita90 Verfasst am: 17. Feb 2014 15:20 Titel: |
 |
|
Oh, entschuldigt bitte. Mir war nicht bewusst, wie vielseitig die Begriffe in Mathematik und Physik benutzt werden.
Es geht tatsächlich eher um einen mathematischen Zusammenhang. Wir haben "integral of motion" definiert als Funktion ) , deren zeitliche Ableitung verschwindet. , deren zeitliche Ableitung verschwindet.
Das trifft auf dein 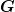 zu. Ich danke dir dafür! zu. Ich danke dir dafür!
Und ich danke auch TomS für seine Mühe und Zeit, auch wenn es mich in dem Fall nicht zur Lösung gebracht hat.
Also noch eine schöne Woche und nochmal: Tut mir leid, dass ich mich so unpräzise ausgedrückt habe. |
|
 |
Margarita90
Anmeldungsdatum: 30.11.2009
Beiträge: 61
|
 Margarita90 Verfasst am: 17. Feb 2014 16:39 Titel: Margarita90 Verfasst am: 17. Feb 2014 16:39 Titel: |
 |
|
Ach und außerdem gilt für ein Integral of Motion F:
=F) , wobei , wobei 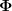 der Fluss ist. der Fluss ist.
Wenn ich noch weiter fragen dürfte: Der Fluss ist doch die Menge der Lösungen der DGL in Abh. von den Anfangsbedingungen, oder?
Um ihn zu bestimmen, löse ich also die DGL, bekomme Integrationskonstanten  und bestimme deren Werte über und bestimme deren Werte über
=x_{10} \in M) und und =x_{20} \in M) . .
Ist das so richtig? |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18062
|
 TomS Verfasst am: 17. Feb 2014 17:53 Titel: TomS Verfasst am: 17. Feb 2014 17:53 Titel: |
 |
|
| Margarita90 hat Folgendes geschrieben: | ... Das trifft auf dein 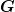 zu ... zu ...
Und ich danke auch TomS für seine Mühe und Zeit, auch wenn es mich in dem Fall nicht zur Lösung gebracht hat. |
Gerne - und schade.
Jetzt schauen wir uns mal an, wie das mit meinen Überlegungen zusammenhängt. Zunächst haben wir



Mit der Definition

folgt

Hat das jetzt irgendwas miteinander zu tun? Die Größe G ist sicher kein Integral der Bewegung im Sinne der Lagrangeschen Mechanik
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Huggy
Anmeldungsdatum: 16.08.2012
Beiträge: 785
|
 Huggy Verfasst am: 18. Feb 2014 09:50 Titel: Huggy Verfasst am: 18. Feb 2014 09:50 Titel: |
 |
|
@Margarita90
Deine Definition von Fluss ist naheliegend. Wirklich bestätigen kann ich sie nicht. In meinem alten Büchlein über DGLs kommt der Begriff Fluss gar nicht vor. Da musst du zur Sicherheit dein Skript konsultieren. Das weitere Vorgehen stimmt dann.
@TomS
Meine gegenwärtige Meinung zur Möglichkeit der physikalischen Interpretation des gegebenen DGL-Systems stimmt mit deiner überein.
Interpretiert man x und y als verallgemeinerte Ortskoordinaten, hätte man ein System mit 2 räumlichen Freiheitsgraden. Die nochmalige Differentiation der DGLs zeigt, dass es zu ihnen kein Potential geben kann und daher auch keine Lagrangefunktion, weil die Integrabilitätsbedingung nicht erfüllt ist.
Interpretiert man x als verallgemeinerte Ortskoordinate und y als kanonisch konjugierten Impuls oder umgekehrt, hätte man ein System mit einem räumlichen Freiheitsgrad. Da auch hier die Integrabilitätsbedingung nicht erfüllt ist, gibt es keine dazu passende Hamiltonfunktion.
| TomS hat Folgendes geschrieben: | So, jetzt hab ich alles zusammen. Es handelt sich um ein freies Teilchen in der komplexen w-Ebene. Die Lagrangefunktion lautet
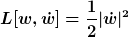
Die Bewegungsgleichungen lauten
 |
Das kann ich allerdings nicht nachvollziehen. Es ist doch dann

Diese L ist also rein reell und führt zu

was man auch zu

zusammenfassen kann. Dieses System erfüllt aber nicht die ursprünglichen DGLs.
@Margarita90
Wäre für die DGL der Trajektorien die Integrabilitätsbedingung erfüllt, entspräche das "Erste Integral" der DGL der Hamiltonfunktion. Seine Konstanz auf den Trajektorien entspricht dann dem Satz, das die Hamiltonfunktion auf den Trajektorien im (q, p)-Raum konstant ist. Es gibt also schon Verbindungen zwischen dem rein mathematisch definierten "Ersten Integral" und den physikalischen Bewegungsintegralen. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18062
|
 TomS Verfasst am: 18. Feb 2014 12:28 Titel: TomS Verfasst am: 18. Feb 2014 12:28 Titel: |
 |
|
| Huggy hat Folgendes geschrieben: | @TomS
Meine gegenwärtige Meinung zur Möglichkeit der physikalischen Interpretation des gegebenen DGL-Systems stimmt mit deiner überein. |
Ja, passt, danke für die Bestätigung.
| Huggy hat Folgendes geschrieben: | | TomS hat Folgendes geschrieben: | | Es handelt sich um ein freies Teilchen in der komplexen w-Ebene |
Das kann ich allerdings nicht nachvollziehen … |
Du hast einen wesentlichen Punkt übersehen:
| TomS hat Folgendes geschrieben: | Nun kann man eine komplexe Funktion z(w) der Form

einführen … Die Lagrangefunktion in z lautet dann

… |
Das hier diskutierte System in der z-Ebene mit z=x+iy wird durch die von oben eingeführte Transformation z=-2/w auf das freie Teilchen in der w-Ebene abgebildet.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18062
|
 TomS Verfasst am: 18. Feb 2014 13:46 Titel: TomS Verfasst am: 18. Feb 2014 13:46 Titel: |
 |
|
Aus

sowie

folgt


Die Bewegungsgleichung
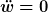
wird dann zu

Diese Gleichung ist mit p = const. und
 = \dot{z}^2 + z\ddot{z} )
identisch erfüllt.
Berechnen wir doch mal den Ausdruck für p auf Basis der ursprünglichen Bewegungsgleichungen
}{x^2-y^2+2ixy} )
Setzen wir nun die ursprüngliche gegebenen Bewegungsgleichungen im Zähler ein, so folgt

Damit ergibt sich wieder meine Schlussfolgerung
| TomS hat Folgendes geschrieben: | … die ursprünglichen Gleichungen waren m.E. nicht die allgemeinen Bewegungsgleichungen, sondern bereits die Gleichungen für einen speziellen Wert
 |
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Huggy
Anmeldungsdatum: 16.08.2012
Beiträge: 785
|
 Huggy Verfasst am: 19. Feb 2014 08:17 Titel: Huggy Verfasst am: 19. Feb 2014 08:17 Titel: |
 |
|
| TomS hat Folgendes geschrieben: | | Huggy hat Folgendes geschrieben: | | TomS hat Folgendes geschrieben: | | Es handelt sich um ein freies Teilchen in der komplexen w-Ebene |
Das kann ich allerdings nicht nachvollziehen … |
Du hast einen wesentlichen Punkt übersehen:
| TomS hat Folgendes geschrieben: | Nun kann man eine komplexe Funktion z(w) der Form
 |
|
Mein Fehler! An die Transformation z <-> w hatte ich in dem Moment nicht mehr gedacht. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18062
|
 TomS Verfasst am: 19. Feb 2014 08:20 Titel: TomS Verfasst am: 19. Feb 2014 08:20 Titel: |
 |
|
Macht nichts ;-)
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
|
















