| Autor |
Nachricht |
Sirius
Anmeldungsdatum: 22.11.2008
Beiträge: 119
|
 Sirius Verfasst am: 30. Dez 2013 18:07 Titel: Konservatives System (Newton - Lagrange) Sirius Verfasst am: 30. Dez 2013 18:07 Titel: Konservatives System (Newton - Lagrange) |
 |
|
Hallo,
in der Newton'schen Mechanik definiert man ein konservatives System als ein System, in dem nur konservative Kräfte vorherrschen. Ein einzelner Massenpunkt (zeitl. konstante Masse) mit der Bewegungsgleichung

ist ein konservatives "System", wenn gilt:
=-\mathbf{F}\cdot\dot{\mathbf{r}}\quad\text{bzw.}\quad\mathbf{F}=-\nabla V(\mathbf{r}))
In der Kraft  sind sowohl treibende Kräfte sind sowohl treibende Kräfte  als auch eventuelle Zwangskräfte als auch eventuelle Zwangskräfte  vorhanden, d.h. das Potential definiert sich über diese beiden Anteile: vorhanden, d.h. das Potential definiert sich über diese beiden Anteile:
=\mathbf{K}+\mathbf{Z})
Ist  also konservativ, dann ist die gesamte mechanische Energie des Massenpunkts erhalten, also also konservativ, dann ist die gesamte mechanische Energie des Massenpunkts erhalten, also
=\text{const})
Bei der Herleitung der Lagrange'schen Bewegungsgleichungen wird zunächst das Prinzip der virtuellen Arbeit ausgenutzt (hier für ein Teilchen), was mit der Newton'schen Bewegungsgleichung auf das d'Alembert'sche Prinzip führt:
\cdot\delta\mathbf{r}=0)
Schreibt man das ganze nun noch auf  generalisierte Koordinaten um, so erhält man: generalisierte Koordinaten um, so erhält man:

Ein konservatives System wird dann charakterisiert als:

Anschließend definiert man die Lagrange-Funktion, um die  in die partiellen Ableitungen hineinziehen zu können. in die partiellen Ableitungen hineinziehen zu können.
Hier stellt sich mir die Frage, ob obige Aussage für ein konservatives System das gleiche ist, wie die für ein konservatives System in der Newton'schen Mechanik, welches ja auch die Zwangskräfte im Potential beinhaltet? Später stoße ich nämlich auf das Problem der Interpretation der Erhaltungsgröße 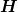 (Hamilton-Funktion), die nur im Falle konservativer (nach Lagrange'scher Definition), holonom-skleronomer Systeme als Gesamtenergie interpretiert werden darf. Bei konservativen, holonom-rheonomen Systemen ist (Hamilton-Funktion), die nur im Falle konservativer (nach Lagrange'scher Definition), holonom-skleronomer Systeme als Gesamtenergie interpretiert werden darf. Bei konservativen, holonom-rheonomen Systemen ist  hingegen keine Erhaltungsgröße, was für mich auf den ersten Blick im Widerspruch zur Newton'schen Mechanik steht. Liegt der Grund dafür also tatsächlich in der unterschiedlichen Definition der Potentiale bzw. eines "konservativen Systems"? hingegen keine Erhaltungsgröße, was für mich auf den ersten Blick im Widerspruch zur Newton'schen Mechanik steht. Liegt der Grund dafür also tatsächlich in der unterschiedlichen Definition der Potentiale bzw. eines "konservativen Systems"? |
|
 |
kingcools
Anmeldungsdatum: 16.01.2011
Beiträge: 700
|
 kingcools Verfasst am: 30. Dez 2013 18:27 Titel: kingcools Verfasst am: 30. Dez 2013 18:27 Titel: |
 |
|
H ist nicht identisch mit T + V aus dem von dir genannten Grund, d.h. die Hamiltonfunktion ist nicht identisch mit dem Energieerhaltungssatz.
Nur für dH/dt = 0 gilt, dass H identisch T + V ist. |
|
 |
Sirius
Anmeldungsdatum: 22.11.2008
Beiträge: 119
|
 Sirius Verfasst am: 30. Dez 2013 20:03 Titel: Sirius Verfasst am: 30. Dez 2013 20:03 Titel: |
 |
|
Vielen Dank schon mal für die Antwort!
Was mich noch interessieren würde ist, ob der Begriff "konservativ" wirklich unterschiedlich definiert ist?
Als Beispiel kann ich eine gleitende Perle auf einem Draht nennen, der mit einem Ende an der z-Achse eines Koordinatensystems befestigt ist und um diese mit der konstanten Winkelgeschwindikeit  rotiert. Es wirke dabei weder Schwerkraft noch Reibung. rotiert. Es wirke dabei weder Schwerkraft noch Reibung.
Die Newton'sche Bewegungsgleichung in ebenen Polarkoordinaten ist dann:
\mathbf{e}_r+2\dot{r}\omega\mathbf{e}_\varphi)
Bildet man z.B. die Rotation der rechten Seite, so sieht man, dass das System nicht-konservativ ist.
Schaue ich mir die gleiche Aufgabe im Lagrange-Formalismus an, so sehe ich zunächst eine skleronome Zwangsbedingung (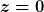 ) und eine rheonome ( ) und eine rheonome ( ). Das System wird hier aber als konservativ angenommen und die Lagrange'schen Bewegungsgleichungen als gültig angenommen. ). Das System wird hier aber als konservativ angenommen und die Lagrange'schen Bewegungsgleichungen als gültig angenommen.
Wie passt das zusammen? Liegt es daran, dass die Zwangkraft, die die rheonome Zwangsbedingung realisiert, im Newton'schen Formalismus mit auftaucht und das System dort nicht-konservativ macht? |
|
 |
Namenloser324
Gast
|
 Namenloser324 Verfasst am: 30. Dez 2013 20:26 Titel: Namenloser324 Verfasst am: 30. Dez 2013 20:26 Titel: |
 |
|
|
Die Zwangskräfte in deinem Beispiel leisten (in Summe) keine Arbeit, daher ist das System konservativ. Falls die Zwangskräfte Arbeit leisten ist das System allerdings auch nicht konservativ. |
|
 |
Sirius
Anmeldungsdatum: 22.11.2008
Beiträge: 119
|
 Sirius Verfasst am: 31. Dez 2013 14:21 Titel: Sirius Verfasst am: 31. Dez 2013 14:21 Titel: |
 |
|
|
Warum leisten die Zwangskräfte in Summe in meinem Beispiel keine Arbeit? Es gibt doch nur eine Zwangskraft (zur Realisierung der Drehung) und die leistet tatsächlich Arbeit. Meinst du vielleicht, dass keine virtuelle Arbeit in Summe geleistet wird? |
|
 |
kingcools
Anmeldungsdatum: 16.01.2011
Beiträge: 700
|
 kingcools Verfasst am: 31. Dez 2013 14:44 Titel: kingcools Verfasst am: 31. Dez 2013 14:44 Titel: |
 |
|
Pardon, ich hatte eine andere Anordnung im Kopf.
Dein Beispiel ist NICHT konservativ. Die Gesamtenergie ist nicht erhalten, denn die Perle gewinnt stetig an Energie und es gibt kein Potential welches dies "auffangen" könnte. Folglich kann T + V auch gar nicht konstant sein.
Hier leistet die Zwangskraft Arbeit, der Antrieb pumpt quasie Energie ins System. |
|
 |
Sirius
Anmeldungsdatum: 22.11.2008
Beiträge: 119
|
 Sirius Verfasst am: 31. Dez 2013 15:02 Titel: Sirius Verfasst am: 31. Dez 2013 15:02 Titel: |
 |
|
Genau hier komme ich aber in Konflikt mit dem Begriff konservativ, denn die Bewegungsgleichung der Perle auf dem Draht kann anscheinend mit den Lagrange'schen Bewegungsgleichungen zweiter Art hergeleitet werden, die für konservative, holonome Systeme gelten. Offenbar ist das System aber eben gerade nicht-konservativ.
Daher ist meine Vermutung ja die, dass in der Lagrange-Mechanik der Begriff "konservativ" die Zwangskräfte nicht einbezieht. |
|
 |
kingcools
Anmeldungsdatum: 16.01.2011
Beiträge: 700
|
 kingcools Verfasst am: 31. Dez 2013 15:27 Titel: kingcools Verfasst am: 31. Dez 2013 15:27 Titel: |
 |
|
Das Beispiel stammt aus dem Nolting, oder? Hab den auch gerade vor mir liegen. In meinen Augen ist das System nicht konservativ, denn die Gesamtenergie ist nicht erhalten.
Jedoch lassen sich die nicht Zwangskräfte, das sind die relavanten für die Lagrangegleichung da ja bekanntlich die Zwangskräfte rausfallen, alle aus einem Potential ableiten (dem Nullpotential bzw. einem anderen konstanten), deswegen lässt sich das System auch mit der Lagrangegleichung 2. Art beschreiben.
Der Begriff des konservativen Systems ist hier meines Erachtens nach falsch, denn darin steckt ja die Bedeutung des Bewahrens.
An sich ist der Begriff aber in der Analytischen Mechanik nicht anders zu verstehen als in der Newtonschen. |
|
 |
Sirius
Anmeldungsdatum: 22.11.2008
Beiträge: 119
|
 Sirius Verfasst am: 31. Dez 2013 16:53 Titel: Sirius Verfasst am: 31. Dez 2013 16:53 Titel: |
 |
|
|
Genau, das Beispiel ist aus dem Nolting. Ich finde es auch ziemlich verwirrend, dass dort von einem konservativen System gesprochen wird, wenn nur die äußeren Kräfte von einem Potential ableitbar sind (siehe Gl. 1.28 ). Normalerweise muss ja die Gesamtkraft konservativ sein, also äußere Kräfte + Zwangskräfte (siehe Gl. 1.17), damit die Energie erhalten ist. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18025
|
 TomS Verfasst am: 31. Dez 2013 17:59 Titel: TomS Verfasst am: 31. Dez 2013 17:59 Titel: |
 |
|
Ich halte die Diskussion über konservative Kräfte für ziemlich verwirrend.
Notwendig und hinreichend für die Energieerhaltung ist, dass die Lagrangefunktion als Ganzes (inkl. Zusatztermen mit Lagrangemultiplikatoren für Zwangsbedingungen) invariant bzgl. Zeittranslationen ist.
Die Frage, ob Gradientenfelder vorliegen ist sekundär. Wenn das Integral über ein geschlossenes Kraftfeld Null ist, bzw. wenn ein Gradientenfeld vorliegt, dann spricht man von einer konservativen Kraft. Und damit ist implizit auch gemeint, dass das zugrundeliegende Potential nicht explizit zeitabhängig ist.
Aber es gibt auch nicht-konservative Kräfte, die sich nicht aus einem skalaren Potential ableiten lassen, und für die dennoch Energieerhaltung gilt. Einfachstes Beispiel sind Magnetfelder.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Sirius
Anmeldungsdatum: 22.11.2008
Beiträge: 119
|
 Sirius Verfasst am: 31. Dez 2013 20:38 Titel: Sirius Verfasst am: 31. Dez 2013 20:38 Titel: |
 |
|
|
Ok, das leuchtet mir soweit ein. Trotzdem verstehe ich nicht, warum das System in obigem Beispiel, in dem die Energie nicht erhalten ist, im Nolting als konservativ bezeichnet wird. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18025
|
 TomS Verfasst am: 01. Jan 2014 09:06 Titel: TomS Verfasst am: 01. Jan 2014 09:06 Titel: |
 |
|
Die Perle auf dem Draht führt eine Rotation in der xy-Ebene durch, sowie eine lineare Bewegung entlang des Drahtes; erstere ist erzwungen, letztere ist aus den Bewegungsgleichungen zu bestimmen. Man formuliert das Problem nun nicht in Koordinaten x,y,z sondern in r und phi; z setzen wir der Einfachheit halber direkt Null; dann gilt:
 - \lambda(\phi - \psi(t)))
lambda steht für den Lagrangemultiplikator, und psi steht für die Winkelkoordinate des Drahtes; im einfachsten Fall einer konstanten Rotation gilt

aber man kann auch allgemeinere Zeitabhängigkeiten beschreiben.
Die Kräfte (hier: reine Zwangskräfte) sowie die Zwangsbedingung selbst folgen nun formal durch Gradientenbildung
))
Das System ist offensichtlich über psi explizit zeitabhängig, d.h. es liegt (außer in Spezialfällen) keine erhaltene Gesamtenergie vor.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Sirius
Anmeldungsdatum: 22.11.2008
Beiträge: 119
|
 Sirius Verfasst am: 01. Jan 2014 21:20 Titel: Sirius Verfasst am: 01. Jan 2014 21:20 Titel: |
 |
|
Habe nochmal einiges an Rechenarbeit investiert und glaube, dass mein Verständnisproblem mit der Lagrange-Funktion allgemein zu tun, da ich je nach Quelle scheinbar widersprüchliche Sachen dazu lese.
Im Landau/Lifschitz steht z.B.:
Die allgemeinste Formulierung des Bewegungsgesetzes mechanischer Systeme ist durch das Hamilton'sche Prinzip gegeben. Nach diesem Prinzip ist jedes mechanische System durch eine Funktion =L(\mathbf{q},\dot{\mathbf{q}},t)) charakterisiert. Die Bewegung des Systems zwischen zwei Zeitpunkten verläuft dann auf eine solche Weise, dass das Integral charakterisiert. Die Bewegung des Systems zwischen zwei Zeitpunkten verläuft dann auf eine solche Weise, dass das Integral
\,\mathrm{d}t)
extremal wird.
Die  sind hierbei voneinander unahängige, generalisierte Koordinaten. sind hierbei voneinander unahängige, generalisierte Koordinaten.
Hierzu zunächst zwei Fragen:
1) Da es heißt, dies sei die allgemeinste Formulierung, nehme ich an, dass obige Darstellung auch für Systeme mit nicht-holonomen Zwangsbedingungen gilt? Stimmt es, dass man dann obiges Integral unter zusätzlichen Nebenbedingungen extremal werden lassen muss, d.h. die  sind bei nicht-holonomen Zwangsbedinungen nicht mehr unabhängig voneinander? sind bei nicht-holonomen Zwangsbedinungen nicht mehr unabhängig voneinander?
2) Kann man wirklich für alle mechanischen Systeme eine Lagrange-Funktion finden? Wie sieht diese dann aus und vor allem wie komme ich auf deren Gestalt? Das Hamilton'sche Prinzip erlaubt mir ja nur die Herleitung Lagrange'scher Gleichungen, sagt mir aber nichts über die Form der Lagrange-Funktion an sich. Ich kann also die partiellen Ableitungen der Lagrange-Funktion ohne weiteres Wissen erst gar nicht ausführen. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18025
|
 TomS Verfasst am: 01. Jan 2014 21:43 Titel: TomS Verfasst am: 01. Jan 2014 21:43 Titel: |
 |
|
Zu 1) Zwangsbedingungen können zur Lagrangefunktion mittels Lagrangemultiplikatoren addiert werden; habe ich oben an einem Beispiel gezeigt. Nehmen wir Koordinaten q, Zwangsbedingungen Gamma mit Lagrangemultiplikatoren lambda; die ursprüngliche Lagrangefunktion sei
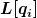
die Zwangsbedingungen

die erweiterte Lagrangefunktion lautet

Die Zwangsbedingungen folgen als Euler-Lagrange-Gleichungen

Die Bewegungsgleichungen folgen als Euler-Lagrangegleichungen aus der erweiterten Lagrangefunktion

Zu 2) Es ist richtig, die Kunst besteht im Finden der Lagrangefunktion. Aber das ist einfacher, als direkt die Bewegungsgleichungen aufzustellen.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Sirius
Anmeldungsdatum: 22.11.2008
Beiträge: 119
|
 Sirius Verfasst am: 02. Jan 2014 15:14 Titel: Sirius Verfasst am: 02. Jan 2014 15:14 Titel: |
 |
|
Vielen Dank, so langsam kommt Licht ins Dunkel! Die Herleitung der Lagrange'schen Bewegungsgleichungen aus dem Hamilton'schen Prinzip müsste ich jetzt verstanden haben.
Nun gibt es ja den Schritt zur Hamiltonfunktion, indem man die Lagrangefunktion ) Legendre-transformiert. Nun steht dazu im Landau/Lifschitz, dass man dabei allgemein von einem unabhängigen Variablensatz zu einem anderen übergeht. In diesem Fall also Legendre-transformiert. Nun steht dazu im Landau/Lifschitz, dass man dabei allgemein von einem unabhängigen Variablensatz zu einem anderen übergeht. In diesem Fall also  . Wie stellt man nun die Hamiltonfunktion eines Systems auf, das nicht-holonomen Zwangsbedingungen unterliegt? In einem solchen Fall sind die . Wie stellt man nun die Hamiltonfunktion eines Systems auf, das nicht-holonomen Zwangsbedingungen unterliegt? In einem solchen Fall sind die  doch nicht unabhängig voneinander. Nimmt man hierzu vielleicht die von dir erwähnte erweiterte Lagrange-Funktion und transformiert sie? doch nicht unabhängig voneinander. Nimmt man hierzu vielleicht die von dir erwähnte erweiterte Lagrange-Funktion und transformiert sie? |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18025
|
 TomS Verfasst am: 02. Jan 2014 15:45 Titel: TomS Verfasst am: 02. Jan 2014 15:45 Titel: |
 |
|
| Sirius hat Folgendes geschrieben: | | Nimmt man hierzu vielleicht die von dir erwähnte erweiterte Lagrange-Funktion und transformiert sie? |
So ist das - in etwa.
Das Problem ist, dass die Legendretransformation in Anwesendheit von Zwangsbedingungen singulär ist. Man benötigt also einen neuen Satz Koordinaten, der explizit zwischen "physikalischen Bewegungen" und "theoretischen Bewegungen in die per Zwangsbedingung verbotene Richtung" unterscheidet. Erstere ergeben dann die physikalische Hamiltonfunktion. Leider sind diese Koordinaten jedoch i.A. nicht explizit bekannt.
Die Unterscheidung zwischen holonom und anholonom ist dabei nicht so entscheidend. Wichtig sind eher sogenannte "primary", "secondary", ... Constraints sowie die Unterscheidung zwischen "first-" und "second-class" Constraints. In Anwesendheit letzterer muss die Poissonklammer durch die sogenannte Dirac-Klammer ersetzt werden.
Leider kenne ich dazu keine gute und zugleich einfache Zusammenfassung. Im Landau und im Goldstein findest du jedenfalls nichts dazu. In der englischen Wikipedia findest du folgendes
http://en.wikipedia.org/wiki/Primary_constraint
http://en.wikipedia.org/wiki/First_class_constraint
http://en.wikipedia.org/wiki/Dirac_bracket
Die Orginalarbeiten von Dirac sind empfehlenswert.
Lies dir dazu mal was durch und stell deine Fragen.
Eine wesentliche Anwendung sind übrigens Feldtheorien mit lokaler Eichsymmetrie.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Sirius
Anmeldungsdatum: 22.11.2008
Beiträge: 119
|
 Sirius Verfasst am: 02. Jan 2014 16:29 Titel: Sirius Verfasst am: 02. Jan 2014 16:29 Titel: |
 |
|
Mein Fokus lag deswegen auf den nicht-holonomen Zwangsbedingungen, da man ja bei Systemen mit ausschließlich holonomen Zwangsbedingungen die Lagrangefunktion immer durch unabhängige Koordinaten ausdrücken und dann die Legendre-Transformation "normal" durchführen kann.
Das mit den Constraints führt wahrscheinlich etwas zu weit für mich, trotzdem danke für deine Links, vielleicht kann ich da später darauf zurückkommen.
Alle Lehrbücher und Quellen die ich bisher gesehen habe, geben die Hamiltonfunktion in der Form
=\sum\limits_ip_i\dot{q}_i-L(\mathbf{q},\dot{\mathbf{q}},t))
an, nachdem sie ) mit dem normalen Verfahren Legendre-transformiert haben. Kann ich davon ausgehen, dass in einem solchen Fall vorausgesetzt wurde, dass keine anholonomen Zwangsbedingungen vorliegen? Ich nehme an, dass man die Lagrangefunktion in der obigen Hamiltonfunktion auch nicht einfach durch die erweiterte ersetzen kann (falls anholonome Zwänge)? mit dem normalen Verfahren Legendre-transformiert haben. Kann ich davon ausgehen, dass in einem solchen Fall vorausgesetzt wurde, dass keine anholonomen Zwangsbedingungen vorliegen? Ich nehme an, dass man die Lagrangefunktion in der obigen Hamiltonfunktion auch nicht einfach durch die erweiterte ersetzen kann (falls anholonome Zwänge)? |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18025
|
 TomS Verfasst am: 02. Jan 2014 16:44 Titel: TomS Verfasst am: 02. Jan 2014 16:44 Titel: |
 |
|
Man muss bei Anwesendheit von constraints immer zunächst die erweiterte Lagrangefunktion sowie die erweiterte Hamiltonfunktion konstruieren. Dann klassifiziert man die constraints nach first- und second-class, dann reduziert man die Hamiltonfunktion ggf. durch explizite Lösung der second-class constraints.
Du hast recht, im Falle holonomer Zwangsbedingungen kann man neue, unabhängige Koordinaten finden. Aber wer sagt dir die? Du musst sie konstruieren. Und der von mir genannte Mechanismus erlaubt dies für alle eine größere Klasse von Zwangsbedingungen.
Du solltest das echt mal lesen, zumindest die Wikipedia-Artikel.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Sirius
Anmeldungsdatum: 22.11.2008
Beiträge: 119
|
 Sirius Verfasst am: 03. Jan 2014 21:08 Titel: Sirius Verfasst am: 03. Jan 2014 21:08 Titel: |
 |
|
Ich muss doch noch mal kurz auf das Hamilton'sche Prinzip zurückkommen, da ich zwei Aussagen dazu gefunden habe, die ich nicht unbedingt vereinen kann:
Landau/Lifschitz:Jedes mechanische System ist durch eine Lagrangefunktion definierbar und die Bewegung zwischen zwei Zeitpunkten verläuft so, dass es dem Hamilton'schen Prinzip genügt.
Goldstein: Das Hamilton'sche Integralprinzip beschreibt die Bewegung mechanischer Systeme, für die alle Kräfte (außer den Randbedingungen) aus einem verallgemeinerten Skalarpotential (das von den Koordinaten der Teilchen, ihren Geschwindigkeiten und der Zeit abhängen kann) ableitbar sind. Solche Systeme heißten monogen.
1) Widersprechen sich jetzt beide Bücher oder sind einfach alle mechanischen Systeme monogen? Hier fällt mir allerdings ein System mit Reibung ein, für dass es meines Wissens nach keine Lagrangefunktion gibt und somit auch das Hamilton'sche Prinzip nicht anwendar ist. Von daher glaube ich eher der Aussage aus dem Goldstein.
2) Ist die Aussage "alle Kräfte (außer den Randbedingungen) aus einem verallgemeinerten Potential herleitbar" gleichzusetzen mit der folgenden Forderung für die generalisierten Kraftkomponenten?

Die fodert man ja z.B. auch, wenn man aus dem d'Alembert'schen Prinzip die Lagrange'schen Gleichungen herleiten will. Das würde für mich aber bedeuten, dass das Hamilton'sche Prinzip in der Mechanik nur aus einem Spezialfall des d'Alembert'schen Prinzips ableitbar ist. Das hört sich für mich auch eher nach einer Bestätigung der Aussage im Goldstein an, da das d'Alembert'sche Prinzip ja oBdA gilt. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18025
|
 TomS Verfasst am: 03. Jan 2014 22:10 Titel: TomS Verfasst am: 03. Jan 2014 22:10 Titel: |
 |
|
Landau spricht von einem Lagrangeschen System, Goldstein von einem Skalarpotential. Mir ist der Zusammenhang nicht offensichtlich klar - und ich mag jetzt nicht in den beiden Büchern suchen. Kannst du noch mehr zum Kontext sagen.
Was ist das U? Ein Potential aus T-U o.ä.? Da gibt es sicherlich allgemeinere Formen, z.b. das relativistische Teilchen.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Jayk
Anmeldungsdatum: 22.08.2008
Beiträge: 1450
|
 Jayk Verfasst am: 03. Jan 2014 23:14 Titel: Jayk Verfasst am: 03. Jan 2014 23:14 Titel: |
 |
|
Ich mische mich einfach mal ein, weil mich das auch etwas verwundert. Im Landau/Lifschitz wird ganz am Anfang das hamiltonsche Prinzip postuliert, alles andere wird darauf aufgebaut:
| Zitat: | §2. Das Prinzip der kleinsten Wirkung
Die allgemeinste Formulierung des Bewegungsgesetzes mechanischer Systeme ist durch das sogenannte Prinzip der kleinsten Wirkung (oder Hamiltonsches Prinzip) gegeben. Nach diesem Prinzip ist jedes mechanische System durch eine bestimmte Funktion charakterisiert:
)
oder in abgekürzter Schreibweise L(q, q., t). Die Bewegung des Systems ergibt sich daraus folgendermaßen:
Angenommen, in den Zeitpunkten t=t1 und t=t2 nehme das System bestimmte Lagen ein, die durch zwei Koordinatenkonfigurationen }) und und }) charakterisiert sind. Die Bewegung des Systems zwischen diesen beiden Lagen verläuft dann auf eine solche Weise, daß das Integral charakterisiert sind. Die Bewegung des Systems zwischen diesen beiden Lagen verläuft dann auf eine solche Weise, daß das Integral
 d t)
den kleinstmöglichen Wert annimmt. (Fußnote: Es muß jedoch darauf hingewiesen werden, daß das Prinzip der kleinsten Wirkung nicht immer für die Bahn im Ganzen gilt, sondern nur für jeden genpgend kleinen Abschnitt; für die gesamte Bahn kann es sich zeigen, daß das Integral (2,1) lediglich einen extremalen, aber nicht einen minimalen Wert annimmt. Dieser Umstand ist jedoch ganz unwesentlich bei der Ableitung der Bewegungsgleichungen, welche nur die Extremalbedingung benutzt.) |
Allerdings wird doch im Landau/Lifschitz später der Impuls als Erhaltungsgröße, die sich aus der Homogenität des Raumes ergibt, definiert, d.h. als  und die Kraft einfach als und die Kraft einfach als  , was ja die Aussage beinhaltet, dass Kräfte aus einem Skalarpotential ableitbar sind. , was ja die Aussage beinhaltet, dass Kräfte aus einem Skalarpotential ableitbar sind.
EDIT: Vergessen zu sagen. Hier wird noch nichts gesagt in die Richtung, dass L=T-U sei oder so. In Kap. VI, §38 werden Zwangsbedingungen behandelt. Kap. VI, §39 wird auch die Form der Lagrange-Funktion für beschleunigte Bezugssysteme hergeleitet |
|
 |
Sirius
Anmeldungsdatum: 22.11.2008
Beiträge: 119
|
 Sirius Verfasst am: 04. Jan 2014 18:59 Titel: Sirius Verfasst am: 04. Jan 2014 18:59 Titel: |
 |
|
Hab nochmal etwas in der Literatur gestöbert und bin mir jetzt sicher, dass das Hamilton'sche Prinzip in der Form
\,\dd t=0\quad\text{mit}\quad\vec{q}=(q_1,\dots,q_s))
dann gilt, wenn sich die generalisierten Kraftkomponenten aus einem verallgemeinerten Skalarpotential ableiten lassen (N Teilchen):
\quad\text{und}\quad j=1,\dots,s)
Für die Lagrangefunktion gilt dann im Allgemeinen immer:
=T(\vec{q},\dot{\vec{q}},t)-U(\vec{q},\dot{\vec{q}},t))
| Jayk hat Folgendes geschrieben: | Allerdings wird doch im Landau/Lifschitz später der Impuls als Erhaltungsgröße, die sich aus der Homogenität des Raumes ergibt, definiert, d.h. als  und die Kraft einfach als und die Kraft einfach als  , was ja die Aussage beinhaltet, dass Kräfte aus einem Skalarpotential ableitbar sind. , was ja die Aussage beinhaltet, dass Kräfte aus einem Skalarpotential ableitbar sind.
EDIT: Vergessen zu sagen. Hier wird noch nichts gesagt in die Richtung, dass L=T-U sei oder so. In Kap. VI, §38 werden Zwangsbedingungen behandelt. Kap. VI, §39 wird auch die Form der Lagrange-Funktion für beschleunigte Bezugssysteme hergeleitet |
Hier muss man aufpassen, da es sich im Allgemeinen ja um generalisierte Koordinaten handelt. Der Zusammenhang

gilt z.B. nicht für ein Teilchen im elektromagnetischen Feld, obwohl sich die Lorentz-Kraft aus einem generalisierten Potential ableiten lässt. Ich kann dir Kapitel 3 aus dem folgenden Skript empfehlen, das hat mir geholfen:
http://wwwcp.tphys.uni-heidelberg.de/admin/vorlesung/mech.pdf |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18025
|
 TomS Verfasst am: 05. Jan 2014 01:43 Titel: TomS Verfasst am: 05. Jan 2014 01:43 Titel: |
 |
|
Die Form L = T - V ist ein Spezialfall
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Sirius
Anmeldungsdatum: 22.11.2008
Beiträge: 119
|
 Sirius Verfasst am: 05. Jan 2014 16:50 Titel: Sirius Verfasst am: 05. Jan 2014 16:50 Titel: |
 |
|
| TomS hat Folgendes geschrieben: | | Die Form L = T - V ist ein Spezialfall |
Ich kann soweit nur für die klassische Mechanik sprechen. Ist es selbst dort nur ein Spezialfall? Wenn ja, wie schaut denn der allgemeinste Fall aus? |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18025
|
 TomS Verfasst am: 05. Jan 2014 21:38 Titel: TomS Verfasst am: 05. Jan 2014 21:38 Titel: |
 |
|
Das einfachste Beispiel für eine andere Form findest du in der Relativitätstheorie sowie für ein nicht-rel. Teilchen im externen el.-mag. Feld.
Und es gibt keine allgemeinste Form.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Sirius
Anmeldungsdatum: 22.11.2008
Beiträge: 119
|
 Sirius Verfasst am: 06. Jan 2014 14:08 Titel: Sirius Verfasst am: 06. Jan 2014 14:08 Titel: |
 |
|
|
Stimmt, ich hätte sagen sollen, dass ich nur von der klassischen nicht-relativistischen Mechanik rede. Dort müsste aber L = T - U schon der allgemeine Fall sein, wenn sich die Kräfte aus einem verallgemeinerten Potential U herleiten lassen, also einem Potential, das auch geschwindigkeitsabhängig sein kann. Dies ist ja z.B. auch bei einem nicht-relativistischen Teilchen im elektromagnetischen Feld möglich. Meintest du mit V vielleicht ein Potential im herkömmlichen Sinne, also ein nur vom Ort und evtl. der Zeit abhängiges? Das wäre dann nämlich tatsächlich ein Speziallfall von U und somit ist dann L = T - V auch ein Spezialfall. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18025
|
 TomS Verfasst am: 06. Jan 2014 15:05 Titel: TomS Verfasst am: 06. Jan 2014 15:05 Titel: |
 |
|
Für ein Teilchen im elektromagnetischen Feld benötigst du den Term
)
wobei es irreführend von mir war, das als nicht-relativistisch zu bezeichnen - sorry. Aber ein Potentialterm ist das nicht, und L = T - V gilt auch nicht.
Ach ja, Bewegungen von Teilchen in Strömungen liefern sicher ebenfalls Beispiele, wo L = T -V nicht gilt.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Sirius
Anmeldungsdatum: 22.11.2008
Beiträge: 119
|
 Sirius Verfasst am: 09. Jan 2014 16:47 Titel: Sirius Verfasst am: 09. Jan 2014 16:47 Titel: |
 |
|
|
Ok, vielen Dank für die zahlreichen Antworten! Auf das mit den Constraints werde ich evtl. zurückkommen, wenn ich Zeit gefunden habe die Artikel durchzulesen. |
|
 |
|















