| Autor |
Nachricht |
TruEnemy
Anmeldungsdatum: 01.11.2010
Beiträge: 516
|
 TruEnemy Verfasst am: 02. Mai 2013 23:29 Titel: Wirkung des harmonischen Oszillators TruEnemy Verfasst am: 02. Mai 2013 23:29 Titel: Wirkung des harmonischen Oszillators |
 |
|
Hallo!
Meine Frage:
Es soll ein 1-dimensionaler harmonischer Oszillator betrachtet und die Wir-
kung 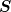 durch Lösen der Hamilton-Jacobi-Gleichung berechnet werden. durch Lösen der Hamilton-Jacobi-Gleichung berechnet werden.
Mein Ansatz:
Leider geht aus der Aufgabe nicht hervor, ob es sich um ein zeitabhängiges
Problem und/oder ein quantenmechanisches Teilchen handelt. Ich nehme mal
einfach beides an. Nach meinem Skript lautet die Hamilton-Jacobi-Gleichung
 = 0 )
Zunächst einmal verwirrt mich die Zeitabhängigkeit der Hamilton-Funktion.
Letztere lautet ja für einen 1-dimensionalen harmonischen Oszillator
^2}{2m} + \frac{1}{2} m\omega_0^2 q^2 )
Wo stecke ich hier die Zeitabhängigkeit rein? Ins Potential? Eingesetzt folgt

Ist das bisher formal korrekt und bin ich auf dem richtigen Weg?
Grüße!
_________________
'Dass ich erkenne, was die Welt im Innersten zusammenhält' Faust, Goethe |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8576
|
 jh8979 Verfasst am: 03. Mai 2013 00:47 Titel: jh8979 Verfasst am: 03. Mai 2013 00:47 Titel: |
 |
|
|
Bis auf einen Tippfehler (die ^2 beim S) ja. Jetzt nur noch lösen mit einem geeigneten Ansatz zur Zeitabhängigkeit. Da dies so ziemlich das Standardbeispiel zur Berechnung der Prinzipalfunktion ist, sollte das nicht so schwer zu finden sein. |
|
 |
TruEnemy
Anmeldungsdatum: 01.11.2010
Beiträge: 516
|
 TruEnemy Verfasst am: 03. Mai 2013 20:30 Titel: TruEnemy Verfasst am: 03. Mai 2013 20:30 Titel: |
 |
|
Ja, du hast Recht, für einen 1-dimensionalen harmonischen Oszillator muss es
 = \frac{\partial S}{\partial t} + \frac{1}{2m} \frac{\partial^2 S}{\partial q_j^2} + \frac{1}{2} m\omega_0^2 q_j^2 = 0 )
mit  = \frac{1}{2m} \left(\frac{\partial S}{\partial q_j}\right)^2+ \frac{1}{2} m\omega_0^2 q_j^2 ) heißen. heißen.
Ich habe mir nun sagen lassen, dass es sich hierbei nicht um ein zeitabhäng-
iges Problem und quantenmechanisches Teilchen handelt, da die Hamilton'
sche charakterisitische Funktion nur für klassische Systeme definiert ist.
Als Lösungsansatz wird wohl wieder - wie sooft - eine e-Funktion dienen?!?
_________________
'Dass ich erkenne, was die Welt im Innersten zusammenhält' Faust, Goethe |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8576
|
 jh8979 Verfasst am: 03. Mai 2013 20:51 Titel: jh8979 Verfasst am: 03. Mai 2013 20:51 Titel: |
 |
|
Wenn die Hamiltonfunktion keine explizite Zeitabhängigkeit enthält, ist S gegeben durch
=S_0(q) - \alpha t)
Fuer eine zu bestimmende Konstante  |
|
 |
TruEnemy
Anmeldungsdatum: 01.11.2010
Beiträge: 516
|
 TruEnemy Verfasst am: 03. Mai 2013 21:10 Titel: TruEnemy Verfasst am: 03. Mai 2013 21:10 Titel: |
 |
|
Jetzt hat's Klick gemacht  Wir betrachten ein zeitunabhängiges Problem Wir betrachten ein zeitunabhängiges Problem
 = \frac{\partial S}{\partial t} + \frac{1}{2m} \frac{\partial^2 S}{\partial q_j^2} + \frac{1}{2} m\omega_0^2 q_j^2 = 0 )
mit  = \frac{1}{2m} \left(\frac{\partial S}{\partial q_j}\right)^2+ \frac{1}{2} m\omega_0^2 q_j^2 ) , also eine zeit- , also eine zeit-
unabhängige Hamilton-Funktion. Könntest Du mir Deinen Ansatz erklären?
 = S(q_j, t = 0) - \alpha t = S_0 (q_j) - \alpha t ) mit mit 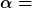 konstant. konstant.
_________________
'Dass ich erkenne, was die Welt im Innersten zusammenhält' Faust, Goethe |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8576
|
 jh8979 Verfasst am: 03. Mai 2013 22:04 Titel: jh8979 Verfasst am: 03. Mai 2013 22:04 Titel: |
 |
|
Es ist vermutlich nur ein Tippfehler, aber
^2 \neq \frac{\partial^2 S}{\partial q_j^2} )
(Ich hab da am Anfang auch nicht so genau hingeschaut um ehrlich zu sein.)
Der Ansatz ist im wesentlichen einfach Trennung der Variablen. Nimm als Ansatz: S(q,t) = S1(q) + S2(t). Dann einsetzen und alles mit S1 auf eine Seite, alles mit S2 auf die andere. Eine Seite hängt dann nur von q ab, die andere nur von t, also muessen beide konstant sein. Das gibt Dir: S2(t)=-a*t. |
|
 |
TruEnemy
Anmeldungsdatum: 01.11.2010
Beiträge: 516
|
 TruEnemy Verfasst am: 03. Mai 2013 22:51 Titel: TruEnemy Verfasst am: 03. Mai 2013 22:51 Titel: |
 |
|
Mensch, klar, das Quadrat einer partiellen Ableitung ist formal nicht weiter
zu vereinfachen. Also haben wir es nun endlich beisammen, denn es ist
 = \frac{\partial S}{\partial t} + \frac{1}{2m} \left( \frac{\partial S}{\partial q_j} \right)^2 + \frac{1}{2} m\omega_0^2 q_j^2 = 0 )
Den Ansatz  = S_1(q) + S_2(t) ) kann ich nachvollziehen, vielen kann ich nachvollziehen, vielen
Dank. Dann werde ich das mal ausführen, was Du mir hier erläutert hast,
und melde mich dann wieder! Vll kommt's mir dann mit der Konstantenbe-
stimmung ...
_________________
'Dass ich erkenne, was die Welt im Innersten zusammenhält' Faust, Goethe |
|
 |
TruEnemy
Anmeldungsdatum: 01.11.2010
Beiträge: 516
|
 TruEnemy Verfasst am: 05. Mai 2013 13:11 Titel: TruEnemy Verfasst am: 05. Mai 2013 13:11 Titel: |
 |
|
Sorry, ich bin nicht mehr dazu gekommen. Ich mach's jetzt schnell:
 + \frac{1}{2m} \left( \frac{\partial}{\partial q_j} S(q_j, t) \right)^2 + \frac{1}{2} m\omega_0^2 q_j^2
<br />
)
 + S_2 (t) \right) + \frac{1}{2m} \left( \frac{\partial}{\partial q_j} \left(S_1(q_j) + S_2 (t) \right) \right)^2 + \frac{1}{2} m\omega_0^2 q_j^2
<br />
)
}{\partial t} + \frac{1}{2m} \left( \frac{\partial S_1(q_j)}{\partial q_j} \right)^2 + \frac{1}{2} m\omega_0^2 q_j^2
<br />
)
}{\partial q_j} \right)^2 + S_0(q_j) = - \frac{\partial S_2 (t)}{\partial t}
<br />
) mit mit  = \frac{1}{2} m\omega_0^2 q_j^2 )
Soweit formal korrekt? Und nun muss - da der linke Ausdruck nur
von q_j, und der rechte nur von t abhängt - beide Parameter kon-
stant sein. (EDIT) Nennen wir diese Konstante also einfach mal c.
_________________
'Dass ich erkenne, was die Welt im Innersten zusammenhält' Faust, Goethe
Zuletzt bearbeitet von TruEnemy am 05. Mai 2013 21:07, insgesamt einmal bearbeitet |
|
 |
TruEnemy
Anmeldungsdatum: 01.11.2010
Beiträge: 516
|
 TruEnemy Verfasst am: 05. Mai 2013 21:06 Titel: TruEnemy Verfasst am: 05. Mai 2013 21:06 Titel: |
 |
|
Also, ich habe nun die zwei folgenden Gleichungen durch Integrieren zu lösen?!
}{\partial q} \right)^2 + \frac{1}{2} m\omega_0^2 q^2 = c = - \frac{\partial S_2(t)}{\partial t}
<br />
)
}{\partial q} \right)^2 + \frac{1}{2} m\omega_0^2 q^2= c
<br />
\Leftrightarrow \boxed{\frac{\partial S_1(q)}{\partial q} = \sqrt{2mc - m^2\omega_0^2 q^2}}
<br />
)
}{\partial t} = -c}
<br />
)
_________________
'Dass ich erkenne, was die Welt im Innersten zusammenhält' Faust, Goethe |
|
 |
TruEnemy
Anmeldungsdatum: 01.11.2010
Beiträge: 516
|
 TruEnemy Verfasst am: 06. Mai 2013 08:53 Titel: TruEnemy Verfasst am: 06. Mai 2013 08:53 Titel: |
 |
|
 = -\int dt\;c = -ct + S_{2,0} )
 = \int dq \;\sqrt{2mc - m^2\omega_0^2 q^2} = \frac{1}{2} \sqrt{2mc - m^2\omega_0^2 q^2} \left( \frac{2c \tan^{-1} \left( \frac{\sqrt{m \omega_0^2 q^2}}{\sqrt{2c - m\omega_0^2 q^2}} \right)}{\omega_0 \sqrt{2mc - m^2\omega_0^2 q^2}} \right) + S_{1,0})
Das Zweite habe ich online berechnen lassen, da bin ich mir nicht sicher. Also ist die Lösung
 = S_1(q) + S_2(t) = \int dq \;\sqrt{2mc - m^2\omega_0^2 q^2} -\int dt\;c
<br />
)
bzw.
 = S_1(q) + S_2(t) = \frac{1}{2} \sqrt{2mc - m^2\omega_0^2 q^2} \left( \frac{2c \tan^{-1} \left( \frac{\sqrt{m \omega_0^2 q^2}}{\sqrt{2c - m\omega_0^2 q^2}} \right)}{\omega_0 \sqrt{2mc - m^2\omega_0^2 q^2}} \right) + S_{1,0} -ct + S_{2,0}
<br />
)
mit 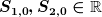 , also zweier Konstanten, die man wohl aus Anfangsbedingungen bekommt? , also zweier Konstanten, die man wohl aus Anfangsbedingungen bekommt?
_________________
'Dass ich erkenne, was die Welt im Innersten zusammenhält' Faust, Goethe |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8576
|
 jh8979 Verfasst am: 06. Mai 2013 09:38 Titel: jh8979 Verfasst am: 06. Mai 2013 09:38 Titel: |
 |
|
S ist (offensichtlich) nur bis auf additive Konstanten bestimmt (und zwei machen in der Weise ja schonmal noch weniger Sinn).
Davon abgesehen muss ich nur einmal googlen um z.B. das hier zu finden:
http://www.uni-tuebingen.de/faessler/Mechanik/ThMetotal7.pdf
Ich versteh ja, dass man um Hilfe fragt, wenn man nicht weiter kommt. Ich versteh nicht, dass man nicht vorher mal selber nach einfach zu findender Hilfe sucht.... |
|
 |
TruEnemy
Anmeldungsdatum: 01.11.2010
Beiträge: 516
|
 TruEnemy Verfasst am: 06. Mai 2013 17:10 Titel: TruEnemy Verfasst am: 06. Mai 2013 17:10 Titel: |
 |
|
Ich verstehe zwar nicht, wieso Du mich jetzt derart 'anpampst', aber OK.
Natürlich hatte ich, bevor ich den Thread gestartet hatte, Google bemüht
und u. a. auch den von Dir besagten Link gefunden und durchgelesen,
allerdings nicht verstanden. Zudem wollte ich es auch selbst rechnen.
Nichtsdestotrotz habe ich eine allgemeine Vorgehensweise und die De-
monstration selbiger am Beispiel des 1-dimensionalen harmonischen
Oszillators im Nolthing gefunden. Heute Abend werde ich es im Detail
durchgehen und die Lösung gegebenenfalls hier posten. Vielen Dank!
_________________
'Dass ich erkenne, was die Welt im Innersten zusammenhält' Faust, Goethe |
|
 |
TruEnemy
Anmeldungsdatum: 01.11.2010
Beiträge: 516
|
 TruEnemy Verfasst am: 06. Mai 2013 23:54 Titel: TruEnemy Verfasst am: 06. Mai 2013 23:54 Titel: |
 |
|
Ich weiß nicht, ob das urheberrechtlich OK wäre, wenn ich die Passage aus
dem Nolting-eBook hier reinstellen würde. Also erläute ich nun Schritt für
Schritt das und auch mein Vorgehen bzgl. des 1-dimensionalen HO:
 = H(q, p) = \frac{1}{2m} p^2 + \frac{1}{2}m \omega_0^2 q^2 ) und mit und mit  folgt folgt
 = \frac{1}{2m} \left( \frac{\partial S}{\partial q}\right)^2 + \frac{1}{2}m \omega_0^2 q^2 )
HJG:  = 0 ) und eingesetzt mit dem Ausdruck von oben: und eingesetzt mit dem Ausdruck von oben:
^2 + \frac{1}{2}m \omega_0^2 q^2 = 0 )
Separationsansatz für  ) : :  = S_1(q, P) + S_2(P, t) ) : :
 + S_2(P, t))}{\partial t} + \frac{1}{2m} \left( \frac{\partial (S_1(q, P) + S_2(P, t))}{\partial q}\right)^2 + \frac{1}{2}m \omega_0^2 q^2 = \frac{\partial S_2(P, t)}{\partial t} + \frac{1}{2m} \left( \frac{\partial S_1(q, P)}{\partial q}\right)^2 + \frac{1}{2}m \omega_0^2 q^2 = 0 )
}{\partial q}\right)^2 + \frac{1}{2}m \omega_0^2 q^2 = - \frac{\partial S_2(P, t)}{\partial t}
<br />
)
Die linke Seite hängt nur von q und die rechte nur von t ab, also sind beide konstant:
}{d q}\right)^2 + \frac{1}{2}m \omega_0^2 q^2 = a
<br />
)
 = m \omega_0 \int dq\;\sqrt{\frac{2a}{m\omega_0^2} - q^2} + S_{1,0}
<br />
)
}{dt} = -a
<br />
)
 = -at + S_{2,0}
<br />
)
Beide Integrationskonstanten sind unbedeutend und können wegbleiben. Zugleich erkannt
man, dass der neue Impuls  der Konstanten entspricht. der Konstanten entspricht.
 = S_1(q, P = a) + S_2(P, t) = m \omega_0 \int dq\;\sqrt{\frac{2a}{m\omega_0^2} - q^2} -at
<br />
)
Also soweit habe ich alles verstanden und ist relativ einfach. Ist damit der Aufgabenteil
"Berechnung der Wirkung S aus der HJG" erledigt? Ja, oder?
Wenn ich nun die Hamilton'sche charakteristische Funktion bei gegebenen Anfangsbeding-
ungen, daraus die jeweils nicht spezifizierte Anfangskoordinate und mit alle dem q(t) be-
rechnen soll, ist damit gemeint, dass ich das Integral in S_1 explizit ausführen soll?
 = 0 ) und und  = 0 )
^{-1/2} - t)
Auch die neue Ortskoordinate Q muss konstant sein, also wählen wir Q =: b:
^{-1/2} - t = b)
 - t = b)
) )
}{dq} = m \omega_0 \frac{d}{dq} \int dq\;\sqrt{\frac{2a}{m\omega_0^2} - q^2} = m \omega_0 \sqrt{\frac{2a}{m\omega_0^2} - q^2} )
Nun kann man q in p einsetzen und erhält:
)} = m \omega_0 \sqrt{\frac{2a}{m\omega_0^2}\left(1 - \sin^2 (\omega_0 (t + b)) \right)} = m \omega_0 \sqrt{\frac{2a}{m\omega_0^2}} \cos (\omega_0 (t + b)) = \sqrt{2ma} \cos (\omega_0 (t + b)) )
Hier müssten nun die Anfangsbedingungen zum Spiel kommen, um die Konstanten a
und b berechnen zu können, oder? Diese dann einsetzen und man hat q(t) und p(t)?
_________________
'Dass ich erkenne, was die Welt im Innersten zusammenhält' Faust, Goethe |
|
 |
TruEnemy
Anmeldungsdatum: 01.11.2010
Beiträge: 516
|
 TruEnemy Verfasst am: 07. Mai 2013 09:23 Titel: TruEnemy Verfasst am: 07. Mai 2013 09:23 Titel: |
 |
|
Bitte, ein kurzes Statement wäre wirklich hilfreich :/
_________________
'Dass ich erkenne, was die Welt im Innersten zusammenhält' Faust, Goethe |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8576
|
 jh8979 Verfasst am: 07. Mai 2013 09:38 Titel: jh8979 Verfasst am: 07. Mai 2013 09:38 Titel: |
 |
|
Nicht jede Kritik ist 'anpampen'.
Aber ganz ehrlich, was möchtest du hören?
Dass der Nolting das richtig gerechnet hat? In jedem Buch oder Skript, das die Hamilton-Jacobi Theorie behandelt und in dem ich gerade nachgeschlagen hab, steht diese Rechnung (Nolting, Greiner, Goldstein, Kuypers,...). Der harmonische Oszillator ist das Standardbeispiel für die Hamilton-Jacobi-Theorie. Möchtest Du, dass ich nachprüfe, ob Du richtig abgeschrieben hast? Langsam wird das wirklich lächerlich... |
|
 |
TruEnemy
Anmeldungsdatum: 01.11.2010
Beiträge: 516
|
 TruEnemy Verfasst am: 07. Mai 2013 09:51 Titel: TruEnemy Verfasst am: 07. Mai 2013 09:51 Titel: |
 |
|
Ich habe hier nichts abgeschrieben! All die Schritte, die ich hier aufgezeichnet habe,
habe ich selbst gerechnet und nur zur Kontrolle mit dem Nolting verglichen! Proble-
me bereitet mir aber OFFENSICHTLICH noch der zweite Teil der Aufgabe: "Hamilton
sche charakteristische Funktion bei gegebenen Anfangsbedingungen, daraus die je-
weils nicht spezifizierte Anfangskoordinate und mit alle dem q(t) berechnen".
Zudem weiß ich nicht, was an meinen FRAGEN, die ich gestellt habe, lächerlich sein soll.
Wie verfahre ich hier denn nun, ausgehend von meiner ermittelten Wirkung S?
Ich habe die Anfangsbedingungen  = 0 ) und und  = 0 ) . .
und bereits die Formeln für , p(a, q) ) hergeleitet: hergeleitet:
) )

Es ist doch jetzt wahrscheinlich das Ziel, mit Hilfe der Anfangsbedingungen a
und b herauszufinden, oder?? Diese in q einzusetzen, bringt erst ein Mal nichts.
Daher nehme ich an, diese erst ein Mal in p einsetzen zu müssen??

_________________
'Dass ich erkenne, was die Welt im Innersten zusammenhält' Faust, Goethe |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8576
|
 jh8979 Verfasst am: 07. Mai 2013 09:57 Titel: jh8979 Verfasst am: 07. Mai 2013 09:57 Titel: |
 |
|
| TruEnemy hat Folgendes geschrieben: | Ich habe hier nichts abgeschrieben! All die Schritte, die ich hier aufgezeichnet habe,
habe ich selbst gerechnet und nur zur Kontrolle mit dem Nolting verglichen! |
Und jetzt schreibst Du es hier nochmal hin, damit wir es nochmal abgleichen? Ganz ehrlich, merkst Du es wirklich nicht...
Im Englischen gibt es ein schönes Wort für dieses Verhalten: Neediness. |
|
 |
TruEnemy
Anmeldungsdatum: 01.11.2010
Beiträge: 516
|
 TruEnemy Verfasst am: 07. Mai 2013 10:00 Titel: TruEnemy Verfasst am: 07. Mai 2013 10:00 Titel: |
 |
|
Jetzt reicht's langsam. Ja, von mir aus hätte ich den Weg bis zu S
weglassen können. Aber wie oft muss ich noch betonen, dass ich
beim zweiten Aufgabenteil Probleme habe? Das ist doch wohl of-
fensichtlich! Und Nein, das ist nicht im Nolting angegeben. Also
bitte ich hier um Hilfe, weil ich nicht weiterkommen! Meine Güte!
_________________
'Dass ich erkenne, was die Welt im Innersten zusammenhält' Faust, Goethe |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8576
|
 jh8979 Verfasst am: 07. Mai 2013 10:03 Titel: jh8979 Verfasst am: 07. Mai 2013 10:03 Titel: |
 |
|
| TruEnemy hat Folgendes geschrieben: | | Jetzt reicht's langsam. |
Seh ich ähnlich... |
|
 |
TruEnemy
Anmeldungsdatum: 01.11.2010
Beiträge: 516
|
 TruEnemy Verfasst am: 07. Mai 2013 10:10 Titel: TruEnemy Verfasst am: 07. Mai 2013 10:10 Titel: |
 |
|
Du ignorierst einfach den Sachverhalt, dass es jetzt um einen Aufgabenteil
geht, den ich nicht irgendwo nachschlagen kann (bzw. dazu nichts finde)
und bei dem ich offensichtlich Probleme habe. Und deine Hilfe beschränkt
sich in dem Punkt nur auf den Verweis, dass ich mir den Aufschrieb bis
zum Punkt der ermittelten Wirkung hätte sparen können. Davon mal ab-
gesehen, hast du vorher schon in keinster Weise geholfen. Es ist schon toll,
andere zu verhöhnen, sich selbst ins Fäustchen zu lachen und für den Größten
zu halten, nur weil man 'nen Link gepostet hat. Ja, Neediness, aber von dir.
_________________
'Dass ich erkenne, was die Welt im Innersten zusammenhält' Faust, Goethe |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8576
|
 jh8979 Verfasst am: 08. Mai 2013 03:51 Titel: jh8979 Verfasst am: 08. Mai 2013 03:51 Titel: |
 |
|
| TruEnemy hat Folgendes geschrieben: | Du ignorierst einfach den Sachverhalt, dass es jetzt um einen Aufgabenteil
geht, den ich nicht irgendwo nachschlagen kann (bzw. dazu nichts finde)
und bei dem ich offensichtlich Probleme habe. Und deine Hilfe beschränkt
sich in dem Punkt nur auf den Verweis, dass ich mir den Aufschrieb bis
zum Punkt der ermittelten Wirkung hätte sparen können. |
1. Ich hab gerade im Nolting (8.Auflage) nachgeschlagen. Es steht drin. Genau das Beispiel des harmonischen Oszillators ist dort ausführlich vorgerechnet, inklusive wie man die Anfangsbedingungen benutzt.
2. Den Aufgaben, nach denen Du fragst, zu urteilen bist Du nicht mehr im ersten Semester. Wenn Du also zwei Funktionen q(t) und p(t) mit Variablen a und b hast, dann solltest Du in der Lage sein aus q(0) und p(0) a und b zu bestimmen.
3. Nicht immer nur rechnen, sondern auch mal nachdenken: Wenn Du einen harmonischen Oszillator hast mit q(0)=0 und p(0)=0, was passiert dann wohl? Die Lösung solltest Du ohne zu Rechnen hinschreiben können.
| Zitat: |
Davon mal ab-
gesehen, hast du vorher schon in keinster Weise geholfen. Es ist schon toll,
andere zu verhöhnen, sich selbst ins Fäustchen zu lachen und für den Größten
zu halten, nur weil man 'nen Link gepostet hat. Ja, Neediness, aber von dir. |
Ich habe Dich ganz sicher nicht verhöhnt und lach mir nicht ins Fäustchen. Den Link hab ich gepostet, weil ich keine Lust hatte das alles hier selber aufzuschreiben, gerade weil es ein Standardbeispiel ist, das man überall finden kann. Und da versteh ich dann auch nicht dass Du das nicht selber finden kannst oder willst. Das zeugt imho von Faulheit und wenig Respekt den Leuten hier gegenüber, die Dir helfen sollen (und wollen).
Und 'Neediness' hast Du offensichtlich nicht verstanden:
Es beschreibt Deine Art eine Rechnung anscheinend nicht selbstständig durchführen zu wollen, sondern bei jedem kleinen Schritt nachzufragen, anstatt einfach mal zu rechnen und gucken was passiert (und was man u.U. korrigieren muss).
Glaub mir: Physik lernt man nicht dadurch, dass man es immer erklärt kriegt, sondern dadurch dass man es selber macht; Versucht einen Weg zu finden, sich verläuft, es falsch macht (wichtig!), neu anfängt, eine Ahnung kriegt wie es gehen könnte, sich überlegt wieso dieser Weg dann wohl richtig sein könnte, korrigiert, sich verbessert... usw... bis man am Ende hoffentlich auf das richtige Ergebnis kommt. Und bevor man andere fragt sollte man diesen Weg zumindest schon ein wenig alleine gegangen sein (und wenn man eine Antwort erhalten hat, versuchen wieder alleine weiterzukommen). Und dieses selber machen sieht man bei Dir so gut wie gar nicht. Es mag sein dass Du es tust, aber man merkt es nicht wirklich, daran was Du fragst, wie Du es fragst und -nicht unwesentlich- wie schnell nach einer Antwort Du wieder fragst...
Das ist nicht böse gemeint, sondern nur ein Tipp wie man Physik lernt (ob Du mir glaubst, dass ich wovon ich rede, oder nicht). Wenn Du meinen Ton verletzend fandest, tut es mit leid. Verletzend ist es ganz sicher nicht gemeint. |
|
 |
TruEnemy
Anmeldungsdatum: 01.11.2010
Beiträge: 516
|
 TruEnemy Verfasst am: 08. Mai 2013 16:00 Titel: TruEnemy Verfasst am: 08. Mai 2013 16:00 Titel: |
 |
|
Spar's Dir, ich habe alles gesagt, was von meiner Seite her zu sagen war. Danke.
_________________
'Dass ich erkenne, was die Welt im Innersten zusammenhält' Faust, Goethe |
|
 |
|
















 Wir betrachten ein zeitunabhängiges Problem
Wir betrachten ein zeitunabhängiges Problem