| Autor |
Nachricht |
Elektriker345
Gast
|
 Elektriker345 Verfasst am: 03. Aug 2005 16:37 Titel: Kirchhoffsche Regel(schweres Beispiel) Elektriker345 Verfasst am: 03. Aug 2005 16:37 Titel: Kirchhoffsche Regel(schweres Beispiel) |
 |
|
Hallo
Ich hab ein Problem das ich nicht lösen kann. Ich will den Ersatzwiderstand, und die Teilsapnnungen berechnen für die untere Schaltung.
+______R1_____R4___
| | |
| | |
| R3 |
| | |
R2_______ |___R5__| -
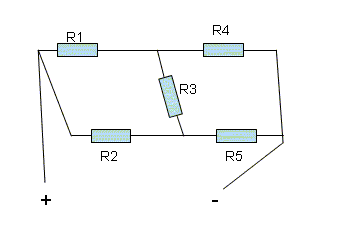
R1,R2,R3,R4,R5 und die Spannung zwischen + und - ist bekannt.
Auserdem, könnte mir jemand die Maschenregel genauer erklären.
Danke im Vorraus
|
|
 |
elektrik345
Gast
|
 elektrik345 Verfasst am: 03. Aug 2005 16:40 Titel: elektrik345 Verfasst am: 03. Aug 2005 16:40 Titel: |
 |
|
oops
da hats ein problem gegeben, sollte etwa so aussehen, nur ohne Punkte.
+______R1_____R4___
| ..................| ...........|
| .................| ...........|
|................ R3 .........|
| ................| ...........|
R2_______ |___R5__| -
|
|
 |
sax

Anmeldungsdatum: 10.05.2005
Beiträge: 377
Wohnort: Magdeburg
|
 sax Verfasst am: 03. Aug 2005 17:38 Titel: sax Verfasst am: 03. Aug 2005 17:38 Titel: |
 |
|
|
am besten zeichen die Schaltung nochmal mit paint oder so, und hänge sie an, auf deiner Zeichung ist nicht wirklich was zu erkennen, ich weiß zum Beispiel nicht wo die Kontakte bei bei R_5 (leks oer rechts vom widerstand) liegen.
|
|
 |
Dieter5858
Moderator

Anmeldungsdatum: 02.08.2004
Beiträge: 696
Wohnort: Hamburg
|
 Dieter5858 Verfasst am: 03. Aug 2005 17:49 Titel: Dieter5858 Verfasst am: 03. Aug 2005 17:49 Titel: |
 |
|
Obwohls wirklich nicht schön gezeichnet ist kann man doch die Grundfunktion erkeffen.
Du kannst doch damit anfangen ein Ersatzschaltbild zu malen (zeichnen).
Dann siehst du auch wieviele verschiedene Wege der Strom gehen kann, auf dem weg von - zu +.
Man darf mich auch korrigiern :-)
1. Kirchhoffes Gesetz:
Die Summe aller Ströme in einem Knotenpunktist 0.
Kommt durch die unterschiedlichen Vorzeichen der Ströme, zum Knotenpunkt hin und vom Knotenpunkt weg(also alles was da hin fliesst muss auch wieder wegfliessen).
2. Kirchhoffsches Gesetz:
Die Summe aller Spannungen in einer Masche ist 0.
KOmmt dadurch das du eine Spannungsquelle hast die eine Spannung erzeugt, diese Spannung allerding entgegengesetzt der Spannung steht die an deinem Verbraucher verbraucht wird.
sollte man sich merken:-)
|
|
 |
elekrik345
Gast
|
 elekrik345 Verfasst am: 03. Aug 2005 17:54 Titel: elekrik345 Verfasst am: 03. Aug 2005 17:54 Titel: |
 |
|
Ok, hab leider kein paint aber es trotzdem hingekriegt.[/img]
| Beschreibung: |
|
| Dateigröße: |
3.46 KB |
| Angeschaut: |
8523 mal |
|
|
|
 |
elektriker345
Gast
|
 elektriker345 Verfasst am: 03. Aug 2005 18:06 Titel: elektriker345 Verfasst am: 03. Aug 2005 18:06 Titel: |
 |
|
Den Ersatzwiderstand, der Gesamtstrom und die Geamtspannung heisen bei mir R6, I6 und U6.
Die Restlichen Ströme und Spannungen sind nach ihren widerständen benannt, also Un/Rn =In.
Nun ist
I1+I2=I6
I6=I4+I5
I1=I4+I3
I3+I2=I5
Da fehlen doch aber doch noch ein paar gelichungen um alles zu berechnen könne.
|
|
 |
Gast
|
 Gast Verfasst am: 03. Aug 2005 18:20 Titel: Gast Verfasst am: 03. Aug 2005 18:20 Titel: |
 |
|
Sollst du das explizit mit den Kirchoffschen Regeln machen? Ich habe da gerade so positive Erfahrungen mit der Maschenstromanalyse gemacht. ;)
Wenn's schnell gehen soll (und es keine Hausaufgabe ist ^^), kannst du die Schaltung auch simulieren. Ansonsten kannst du ja mal die Widerstände und die Spannung sowie deine Ansätze posten.
Oben ist jetzt nur die Knotenregel verarbeitet, wenn du noch die Maschenregel dazunimmst sollte es klappen.
|
|
 |
Gast
|
 Gast Verfasst am: 03. Aug 2005 19:08 Titel: Gast Verfasst am: 03. Aug 2005 19:08 Titel: |
 |
|
|
ich verstehe aber nicht wie man in dieser Schaltung die Maschenregel anwendet.
|
|
 |
Frank11NR
Anmeldungsdatum: 15.06.2005
Beiträge: 82
|
 Frank11NR Verfasst am: 03. Aug 2005 19:52 Titel: Frank11NR Verfasst am: 03. Aug 2005 19:52 Titel: |
 |
|
Beitrag Editiert, da ich (wenn auch spät) gemerkt hab, dass ein grundlegender saudummer Fehler drin steckt.
Kann Dir aber sagen, dass Du mit einer Dreieck- Stern- Umwandlung weiterkommen müsstest.
Gruß
Frank
Zuletzt bearbeitet von Frank11NR am 04. Aug 2005 00:39, insgesamt einmal bearbeitet |
|
 |
sax

Anmeldungsdatum: 10.05.2005
Beiträge: 377
Wohnort: Magdeburg
|
|
 |
Dieter5858
Moderator

Anmeldungsdatum: 02.08.2004
Beiträge: 696
Wohnort: Hamburg
|
 Dieter5858 Verfasst am: 04. Aug 2005 16:41 Titel: Dieter5858 Verfasst am: 04. Aug 2005 16:41 Titel: |
 |
|
Hi Sax
Sag mal meinst du das ernst mit deinen Gleichungen?
Es ist zwar schon fast bekannt das ich nicht so der Typ für Formeln bin (ok bei dieser Rechnung würde auch ich mir Formeln erstellen und danach rechnen aber das was du da hast ist echt  ). ).
Erstmal zur Maschenregel.
In deinem Netzwerk sehe ich 2 Maschen eine "links" und eine "rechts", der R3 ist in beiden Maschen enthalten.
Bei den Maschen musst du die Widerstände sozusagen im Kreis sehen ein Kreis ergibt immer eine Masche.
Wenn du alle Spannungen an den Widerständen ,mit Pfeilrichtung, einzeichnest wirst du sehen das jeweils ein Pfeil andes gepolt ist als die anderen 2.
Und das dieser eine Pfeil die Spannung der anderen 2 damit "aufhebt".
Nun zu deinem Netzwerk:
Berechne doch einfach über die Widerstandsverhältnisse, dann sollte das ganze etwas leichter gehen.
Dann siehst du auch ganz schnell in welche Richtung der Strom durch R3 fliesst.
|
|
 |
elektriker345
Gast
|
 elektriker345 Verfasst am: 04. Aug 2005 18:27 Titel: elektriker345 Verfasst am: 04. Aug 2005 18:27 Titel: |
 |
|
ok dann gilt also
U1+U3=U2
U4=U3+U5
daraus folgt
R1*I1+R3*I3=R2*I2
R4*I4=R3*I3+R5*I5
und das hat mir noch zur berechnung gefehlt?
|
|
 |
sax

Anmeldungsdatum: 10.05.2005
Beiträge: 377
Wohnort: Magdeburg
|
 sax Verfasst am: 08. Aug 2005 22:14 Titel: sax Verfasst am: 08. Aug 2005 22:14 Titel: |
 |
|
@Dieter5858
Wenn du den Kreis ganz außen lang gehts ist das auch eine Masche, oder wenn du die von der Spannungsquelle über R3, R4 wieder zur Quelle gehst ist auch das ne Masche, die habe ich micht masche oben bezeichnet.
Wahrscheinlich kann man die Aufgabe einfacher Lösen, ich habe einfach nur mal maple schnell ausrechnen lassen, was rauskommt ohne große Überlegungen reinzustecken. Aber letzlich ist es doch nur ein lineares Gleichugssystem mit 6 unbekannten, es ist zwar nicht angenehm sowas per Hand auszurechnen, aber dafür gibts ja Computeralgebrasysteme.
Die Stromrichtungen habe ich nur insofern willkürlich gewählt, um z.B. bei R3 festzulegen an welchem Knoten er positiv und an welchem er negativ gezählt wird, denn einmal muß er ja zufließen und einmal abfließen. Es kann aber immer noch was negatives rauskommen, dann fließt er halt in die andere Richtung.
Ich denke jedenfalls das das Ergebnis richtig ist.
edit: Man kann ja mal einige einfache Spezialfälle anschauen:
a) alle Widerstände sind gleich(R1=R;R2=R usw.). Hier ist aus der Symmetrie sofort ersichtlich, das durch R3 kein Strom fließt, man kann also R1 und R4 als in Reihe geschaltet auffassen, R2 und R5 auch, dann hat man effektiv 2 Parallel geschaltete Widerstände mit dem Widerstand 2R und es kommt als effektiver Widerstand der gesamten Schaltung R raus. Wenn man in meiner Geichung alle Widerstände gleich R setzt kommt auch R raus, das stimmt also schonmal.
b) 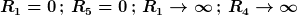
Hier sollte offenbar  rauskommen. Wenn man erstmal rauskommen. Wenn man erstmal  und und  in die obere Gleichung einsetzt und dann in die obere Gleichung einsetzt und dann  und und  gegen unendlich gehen läßt erhält man gegen unendlich gehen läßt erhält man
 , stimmt also auch. Vieleicht kann man es einfacher ableiten, aber wenn meine Geichung stimmt, wird das Ergebnis nicht einfacher aussehen. Solange die ganzen Widerstände frei wählbar sind, kommt eben ein längerer Ausdruck raus. , stimmt also auch. Vieleicht kann man es einfacher ableiten, aber wenn meine Geichung stimmt, wird das Ergebnis nicht einfacher aussehen. Solange die ganzen Widerstände frei wählbar sind, kommt eben ein längerer Ausdruck raus.
|
|
 |
yeti777

Anmeldungsdatum: 10.11.2004
Beiträge: 160
Wohnort: Schweiz
|
 yeti777 Verfasst am: 09. Aug 2005 16:18 Titel: yeti777 Verfasst am: 09. Aug 2005 16:18 Titel: |
 |
|
Hallo sax,
ich habe das Beispiel ebenfalls durchgerechnet und komme exakt auf dasselbe Resultat wie du  ! !
Sei Z der Zähler von  . Z ist ungleich Null, denn er besteht aus einer Summe von lauter positiven Summanden. Für den Strom, der durch . Z ist ungleich Null, denn er besteht aus einer Summe von lauter positiven Summanden. Für den Strom, der durch 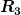 fliesst, gilt: fliesst, gilt: }{Z} ) . Für . Für  folgt daraus, wenn folgt daraus, wenn  ungleich Null ist: ungleich Null ist:  . Das ist die klassische Brückenschaltung für die Bestimmung eines unbekannten Widerstandes, wenn 3 der Widerstände bekannt sind! . Das ist die klassische Brückenschaltung für die Bestimmung eines unbekannten Widerstandes, wenn 3 der Widerstände bekannt sind!
Vielleicht war dies auch der Hintergedanke des Aufgabenstellers.
Gruss yeti
_________________
Ich weiss, dass ich nichts weiss.
Sokrates 470 - 399 v.Ch. |
|
 |
sax

Anmeldungsdatum: 10.05.2005
Beiträge: 377
Wohnort: Magdeburg
|
 sax Verfasst am: 10. Aug 2005 01:04 Titel: sax Verfasst am: 10. Aug 2005 01:04 Titel: |
 |
|
Schön, dann wird es wohl richtig sein.
Ja ja, die Brückenschaltung, haben wir in grauer vorzeit mal im Grundpraktikum benutzt. Das waren noch Zeiten... .Okay solange ist's dann uch wieder nicht her.
Hast du die Aufgabe einfacher gelöst. Ich finde das ist mehr eine Aufgabe um das Lösen von Gleichungssystemen zu üben, als dafür die Knoten und die Maschenregel zu vertiefen.
|
|
 |
Alex
Gast
|
 Alex Verfasst am: 20. Aug 2005 00:02 Titel: Frage zu Kirchhoff u.a. Alex Verfasst am: 20. Aug 2005 00:02 Titel: Frage zu Kirchhoff u.a. |
 |
|
Liebe Physiker!
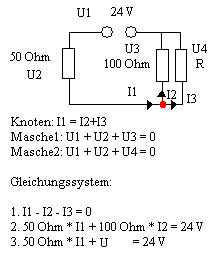
Habe eine Paint Schaltskizze des betreffenden Schaltkreises angefügt.
Gesucht ist die Spannung, die an R abfällt.
Um die Aufgabe zu lösen habe ich die Knoten- und Maschenregel angewandt. Das entstehende Gleichungssystem, bestehend aus 3 Gleichungen und 4 Unbekannten, ist ebenfalls der angefügten Grafik zu entnehmen.
Um eine Lösung erhalten zu können, habe ich eine 4. Gleichung durch ersetzen der drei Widerstände durch einen Ersatzwiderstand erstellt:
4. I1= 24 / ( 50 + (1/100 + 1/(U/I3) )^(-1) )
Schön und gut, gebe alles bei Maple ein und er kann es nicht lösen.
Wo ist mein (Denk-)Fehler? Durch einsetzen der 4. Gleichung in die dritte hat man doch in der 3. nurnoch I1 und I3, und somit ein adäquates Gleichungssystem aus 3 Gleichungen mit 3 Unbekannten.
Oder ist eine Lösung der Aufgabe auf diese Weise nicht möglich, da zuwenig Informationen gegeben sind?
Vielen Dank und ich hoffe auf schnelle Hilfe!
| Beschreibung: |
|
| Dateigröße: |
3.04 KB |
| Angeschaut: |
5511 mal |
|
|
|
 |
yeti777

Anmeldungsdatum: 10.11.2004
Beiträge: 160
Wohnort: Schweiz
|
 yeti777 Verfasst am: 20. Aug 2005 11:52 Titel: yeti777 Verfasst am: 20. Aug 2005 11:52 Titel: |
 |
|
Hallo Alex!
Neben Knoten- und Maschenregeln musst du noch das ohmsche Gesetz bezüglich den Spannungsabfällen über den Widerständen berücksichtigen. Wenn du es richtig machst, erhältst du ein lineares Gleichungssystem für die 5 Unbekannten I1, I2, I3, U2, U4. Der Rang der Matrix ist 5, dh. es existiert eine eindeutige Lösung.
Zur Kontrolle, Spannung über R :  , wobei R1 = 100 [Ohm], R2 = 50 [Ohm]. , wobei R1 = 100 [Ohm], R2 = 50 [Ohm].
Gruss yeti
_________________
Ich weiss, dass ich nichts weiss.
Sokrates 470 - 399 v.Ch. |
|
 |
Alex
Gast
|
 Alex Verfasst am: 20. Aug 2005 15:53 Titel: Alex Verfasst am: 20. Aug 2005 15:53 Titel: |
 |
|
|
Vielen Dank, kannst du mir denn die Gleichungen mal hierreinposten?
|
|
 |
|

















 ).
).
 !
!
