| Autor |
Nachricht |
Erster Admiral
Anmeldungsdatum: 07.05.2021
Beiträge: 69
|
 Erster Admiral Verfasst am: 10. Aug 2021 11:13 Titel: Energie auf kosmologischer Ebene nicht erhalten |
 |
|
Energie ist gemäß des Noether-Theorems aufgrund der Ausdehnung des Universums auf Kosmologischer Ebene nicht erhalten.
Siehe:
https://www.youtube.com/watch?v=ZYM6HMLgIKA
Kann es also sein, dass sich das Universum mit der Zeit einfach auflöst? Quasi einfach verpufft und im Nichts verschwindet? |
|
 |
willyengland
Anmeldungsdatum: 01.05.2016
Beiträge: 676
|
| willyengland Verfasst am: 10. Aug 2021 12:56 Titel: |
|
|
Wenn ich das aktuelle kosmologische Weltbild richtig verstehe, gibt es gegen Ende nur noch schwarze Löcher. Diese zerstrahlen dann auch noch ganz langsam durch die Hawking-Strahlung. Am Ende bleibt also nur ein bisschen Strahlung übrig.
_________________
Gruß Willy |
|
|
Erster Admiral
Anmeldungsdatum: 07.05.2021
Beiträge: 69
|
| Erster Admiral Verfasst am: 10. Aug 2021 13:38 Titel: |
|
|
| willyengland hat Folgendes geschrieben: | | Wenn ich das aktuelle kosmologische Weltbild richtig verstehe, gibt es gegen Ende nur noch schwarze Löcher. Diese zerstrahlen dann auch noch ganz langsam durch die Hawking-Strahlung. Am Ende bleibt also nur ein bisschen Strahlung übrig. |
gemäß der kosmologischen Rotverschiebung sollte diese Reststrahlung aber auch immer weiter an Energie verlieren bis dann eigentlich garnichts mehr vorhanden ist. |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18027
|
| TomS Verfasst am: 10. Aug 2021 14:57 Titel: Re: Energie auf Kosmologischer Ebene nicht erhalten |
|
|
| Erster Admiral hat Folgendes geschrieben: | | Energie ist gemäß des Noether-Theorems aufgrund der Ausdehnung des Universums auf Kosmologischer Ebene nicht erhalten. |
So einfach ist das nicht.
In einem expandierenden Universum kann man eine (erhaltene) Energie als Volumenintegral nicht sinnvoll definieren. Die Energiedichte ist jedoch weiterhin kovariant konstant.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
Erster Admiral
Anmeldungsdatum: 07.05.2021
Beiträge: 69
|
| Erster Admiral Verfasst am: 10. Aug 2021 16:20 Titel: Re: Energie auf Kosmologischer Ebene nicht erhalten |
|
|
| TomS hat Folgendes geschrieben: |
In einem expandierenden Universum kann man eine (erhaltene) Energie als Volumenintegral nicht sinnvoll definieren. Die Energiedichte ist jedoch weiterhin kovariant konstant. |
Kann man aus einer konstanten Energiedichte in einem zunehmenden Volumen keine Zunahme der Energie folgern?
Wie ist das dann mit der kosmologischen Rotverschiebung? Wie in oben erwähntem Video gesagt wird, verschwindet die Energie einfach weil es keine Zeit-translationsinvarianz gibt.
weitere Frage:
Wie kann ich die konstanz der Energie-Dichte eigentlich im Friedmann-Modell verstehen? Da erhält man doch:
=\rho_{mat}(t)c^2=konst \cdot c^2/R(t)^3)
mit dem Skalenfaktor R |
|
|
Erster Admiral
Anmeldungsdatum: 07.05.2021
Beiträge: 69
|
| Erster Admiral Verfasst am: 10. Aug 2021 17:10 Titel: Re: Energie auf Kosmologischer Ebene nicht erhalten |
|
|
| TomS hat Folgendes geschrieben: |
In einem expandierenden Universum kann man eine (erhaltene) Energie als Volumenintegral nicht sinnvoll definieren. Die Energiedichte ist jedoch weiterhin kovariant konstant. |
Ist die Energiedichte denn überhaupt kovariant konstant, wenn keine Zeittranslationsinvarianz gilt? |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18027
|
| TomS Verfasst am: 11. Aug 2021 10:03 Titel: |
|
|
In einer flachen Raumzeit hast du eine erhaltene Energie-Impuls-Dichte
In einer gekrümmten Raumzeit musst du die kovariante Ableitung verwenden, d.h.
^{\mu} = 0)
Die Zustatzterne bewirken, dass weder die Zeitableitung alleine verschwindet, noch direkt ein Volumenintegral für eine erhaltene Energie konstruiert werden kann.
Wenn ein Killing-Feld k existiert, dann folgt ein erhaltenes Vektorfeld
Aber aufgrund der Expansion existiert kein derartiges zeitartiges k.
Es ist jedoch irreführend, zu meinen, die Energieerhaltung wäre verletzt; es ist eher so, dass bereits der Konstruktion der Energie als Volumenintegral nicht sinnvoll ist.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
Günther
Anmeldungsdatum: 23.11.2010
Beiträge: 305
|
| Günther Verfasst am: 11. Aug 2021 11:05 Titel: |
|
|
Für das grundsätzliche Verständnis kommt man ohne Mathe aus:
https://www.preposterousuniverse.com/blog/2010/02/22/energy-is-not-conserved/
In the case of dark energy, that evolution is pretty simple: the density of vacuum energy in empty space is absolute constant, even as the volume of a region of space (comoving along with galaxies and other particles) grows as the universe expands. So the total energy, density times volume, goes up. |
|
|
Erster Admiral
Anmeldungsdatum: 07.05.2021
Beiträge: 69
|
| Erster Admiral Verfasst am: 11. Aug 2021 11:15 Titel: |
|
|
| TomS hat Folgendes geschrieben: | In einer flachen Raumzeit hast du eine erhaltene Energie-Impuls-Dichte
In einer gekrümmten Raumzeit musst du die kovariante Ableitung verwenden, d.h.
Die Zustatzterne bewirken, dass weder die Zeitableitung alleine verschwindet, noch direkt ein Volumenintegral für eine erhaltene Energie konstruiert werden kann.
Wenn ein Killing-Feld k existiert, dann folgt ein erhaltenes Vektorfeld
Aber aufgrund der Expansion existiert kein derartiges zeitartiges k.
Es ist jedoch irreführend, zu meinen, die Energieerhaltung wäre verletzt; es ist eher so, dass bereits der Konstruktion der Energie als Volumenintegral nicht sinnvoll ist. |
ok danke das hilft mir weiter.
Aber folgt dann daraus, dass die photonen-Energie E=hf, wenn man sie in der üblichen weise definiert nicht erhalten ist? |
|
|
Ich
Anmeldungsdatum: 11.05.2006
Beiträge: 913
Wohnort: Mintraching
|
| Ich Verfasst am: 11. Aug 2021 15:21 Titel: |
|
|
| TomS hat Folgendes geschrieben: | | Es ist jedoch irreführend, zu meinen, die Energieerhaltung wäre verletzt; es ist eher so, dass bereits der Konstruktion der Energie als Volumenintegral nicht sinnvoll ist. |
Das sehe ich nicht so. Die Energieerhaltung ist verletzt, eben weil kein zeitartiges Killingfeld vorliegt. Dass die Divergenz des Energie-Impuls-Tensors verschwindet, ist eine andere Aussage.
Das Problem ist auch nicht, dass man kein Volumenintegral definieren könnte. Im Fall einer Friedman-Metrik z.B. hat man eine räumlich konstante Energiedichte und ein vernünftiges Volumenelement, so dass man Energieerhaltung defineren kann als
bzw.
=0)
Stattdessen gilt aber:
=0) .
Das heißt, wenn man die Raumzeit auf Zeit und Raum und entsprechend den Energie-Impuls-Tensor auf Energie und Impuls (Druck) herunterbricht, ist beides nicht erhalten. Impulse dissipieren mit 1/a weg (das ist die Killing-Symmetrie in der FRW-Metrik), und die Energie kann verschwinden oder ins Unendliche wachsen, je nach Druck. Das ist eine direkte Konsequenz daraus, dass die Koordinaten nicht zeitinvariant sind. |
|
|
Erster Admiral
Anmeldungsdatum: 07.05.2021
Beiträge: 69
|
| Erster Admiral Verfasst am: 12. Aug 2021 08:54 Titel: |
|
|
| TomS hat Folgendes geschrieben: |
Aber aufgrund der Expansion existiert kein derartiges zeitartiges k.
Es ist jedoch irreführend, zu meinen, die Energieerhaltung wäre verletzt; es ist eher so, dass bereits der Konstruktion der Energie als Volumenintegral nicht sinnvoll ist. |
Worin genau liegt denn eigentlich das Problem mit dem Volumenintegral?
Ich definiere die Energie jetzt mal als:
 |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18027
|
| TomS Verfasst am: 12. Aug 2021 12:40 Titel: |
|
|
Genau darin liegt das Problem.
Zunächst mal ist die Energiedichte eben nicht durch die Nullkomponente eines Vektorfeldes j sondern durch die 00-Komponente eines Tensorfeldes T gegeben. Zum Vektorfeld j gelangst du nur mittels eines Killingvektorfeldes k, aber ohne dessen Existenz funktioniert das nicht; das Vektorfeld j ist dann nicht erhalten.
Wenn du stattdessen
definierst, dann hat diese Energie E kein vernünftiges Transformationsverhalten. Außerdem funktioniert der bekannte Trick mittels des Oberflächenintegrals und der Kontinuitätsgleichung nicht, da die Kontinuitätsgleichung
^\mu = 0 )
nicht nur Ableitungsterme enthält.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
| index_razor Verfasst am: 12. Aug 2021 13:19 Titel: |
|
|
| Erster Admiral hat Folgendes geschrieben: | | TomS hat Folgendes geschrieben: |
Aber aufgrund der Expansion existiert kein derartiges zeitartiges k.
Es ist jedoch irreführend, zu meinen, die Energieerhaltung wäre verletzt; es ist eher so, dass bereits der Konstruktion der Energie als Volumenintegral nicht sinnvoll ist. |
Worin genau liegt denn eigentlich das Problem mit dem Volumenintegral?
Ich definiere die Energie jetzt mal als:
|
Ich glaube es spricht nichts dagegen. Vielleicht nochmal aus einer etwas algemeineren Perspektive. Lokale Erhaltungssätze haben in gekrümmten (torsionsfreien) Raumzeiten die Form
(Die erste Gleichheit folgt aus der Torsionsfreiheit, aber die zweite gilt universell für lokale Erhaltungsgrößen.) Um aus einem lokal erhaltenen Viererstrom eine Erhaltungsgröße zu berechnen, benutzt man das verallgemeinerte Gaußsche Gesetz
Wenn also  die obige Kontinuitätsgleichung erfüllt und man für 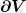 einfach zwei raumartige Hyperflächen zu verschiedenen Zeiten wählt, dann ergibt das also eine konstante Energie nach deiner Definition.
In der allgemeinen Relativitätstheorie gibt es aber im allgemeinen keinen lokal erhaltenen Vektor , der die Vierer-Energie-Impulsstromdichte beschreibt. Warum? Nehmen wir an, wir haben eine Familie von Beobachtern mit 4-Geschwindigkeit  , also
Wegen der kovarianten Konstanz von T gilt also
Würde die rechte Seite verschwinden, dann hätte man also einen erhaltenen Strom, und die von dir definierte Energie wäre erhalten. Die rechte Seite verschwindet aber genau dann, wenn das zeitartige Vektorfeld  die Bedingung
erfüllt (wegen der Symmetrie von T). Die letzte Bedingung ist aber gerade die Bedingung an ein Killingfeld, was eben in der FRW-Raumzeit nicht existiert.
Also die Integration etc. ist nicht das Problem, sondern daß statt  für alle Beobachter lediglich
)
gilt. Also existiert keine lokal erhaltene 4-Stromdichte für Energie und Impuls und dein Integral ist abhängig von der gewählten raumartigen Hyperfläche, sprich: nicht konstant in der Zeit.
Zuletzt bearbeitet von index_razor am 12. Aug 2021 14:39, insgesamt 2-mal bearbeitet |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18027
|
| TomS Verfasst am: 12. Aug 2021 14:02 Titel: |
|
|
Schön erklärt.
(die Integration ist tatsächlich nur für die 00-Komponente eines Tensorfeldes problematisch, nicht für ein Vektorfeld).
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
Erster Admiral
Anmeldungsdatum: 07.05.2021
Beiträge: 69
|
| Erster Admiral Verfasst am: 12. Aug 2021 16:03 Titel: |
|
|
Danke für eure Antworten.
Aber mir ist noch nicht ganz klar was jetzt der Unterschied zwischen
und
ist.
Bzw. was genau ist j^0 überhaupt, wenn T^{00} die eigentliche Energiedichte ist? |
|
|
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
| index_razor Verfasst am: 12. Aug 2021 16:22 Titel: |
|
|
| Erster Admiral hat Folgendes geschrieben: | Danke für eure Antworten.
Aber mir ist noch nicht ganz klar was jetzt der Unterschied zwischen
und
ist.
Bzw. was genau ist j^0 überhaupt, wenn T^{00} die eigentliche Energiedichte ist? |
Der Unterschied besteht lediglich in der Wahl des Koordinatensystems. Für eine beliebige Schar von Beobachtern, repräsentiert durch ein zeitartiges Vektorfeld , ist  der Kovektor der Vierer-Energiestromdichte. Also ist genau  die von diesen Beobachtern gemessene Energiedichte. In einem Koordinatensystem mit  (falls so eins existiert), gilt folglich
also insbesondere  .
Allerdings gilt diese Beziehung, im Gegensatz zu , eben nur in diesem speziellen Koordinatensystem. |
|
|
|
Registrieren
Login
FAQ
Suchen
