| Autor |
Nachricht |
FelixO
Gast
|
 FelixO Verfasst am: 21. Jan 2021 11:16 Titel: Temperatur und Widerstand im Leiter FelixO Verfasst am: 21. Jan 2021 11:16 Titel: Temperatur und Widerstand im Leiter |
 |
|
Meine Frage:
Folgende Aufgabe bereitet mir Probleme:
Ein Widerstand besteht aus zwei Bereichen unterschiedlichen Materials mit gleichem Querschnitt A = 10 mm^2 und den Längen l1 und l1.
Es gilt für 20 Grad: rho1 = 10 , alpha1 = 0,012, rho2 = 5 und alpha2 = -0,008
a) bestimmen Sie allgemein den Gesamtwiderstand R der Anordnung bei 20 Grad und geben Sie für den Fall R = 25 Ohm eine Beziehung zwischen l1 und l2 in der Form l1 = f(l2) an.
b) Die Temperatur ist nun veränderlich.
Bestimmen Sie allgemein den Gesamtwiderstand der Anordnung R(T) und bringen Sie die Beziehung in die Form R(T) = R(bei 20 Grad) + f(l1,l1)*(delta)T
c) Es soll nun unabhängig von der Temperatur gelten R(T) = 25 Ohm
Bestimmen Sie konkrete Längen l1 und l2
Meine Ideen:
a) Hier habe ich überhaupt keine Idee, wie ich da vorgehen soll. Die Aufgabenstellung leuchtet mir auch nicht ganz ein, was genau ist hier die Vorgehensweise und wie müsste das Ergebnis (nur allgemeiner Form, richtig?) aussehen?
b) Selbiges hier...
c) Hier habe ich für l1 = 25m und für l2 = 50m raus. Ist das soweit korrekt?
Ich wäre wirklich mehr als dankbar für Unterstützung! |
|
 |
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5850
|
 Myon Verfasst am: 21. Jan 2021 15:01 Titel: Re: Temperatur und Widerstand im Leiter Myon Verfasst am: 21. Jan 2021 15:01 Titel: Re: Temperatur und Widerstand im Leiter |
 |
|
a) Gegeben sind der spezifische Widerstand und die Temperaturkoeffizienten alpha (die Grössen haben übrigens eine Einheit;)). Nun R in Abh. von l1, l2 ausdrücken. Falls der Zusammenhang zw. Widerstand und spezifischem Widerstand nicht bekannt ist, hier nachschauen. Dann diese Gleichung für R nach l1 auflösen.
b) Auch hier hilft ein Blick in den obigen Wikipedia-Artikel. Dort ist angegeben, wie der spezifische Widerstand von der Temperatur abhängt bei gegebenem Koeffizienten alpha. |
|
 |
FelixO
Gast
|
 FelixO Verfasst am: 21. Jan 2021 15:44 Titel: FelixO Verfasst am: 21. Jan 2021 15:44 Titel: |
 |
|
Danke, ich hab mir den Artikel durchgelesen. Das haben wir allerdings auch schon alles in den Vorlesungen thematisiert.
Dennoch habe ich Schwierigkeiten beim Aufstellen der Gleichungen... ich komme genau wie vorher nicht weiter. |
|
 |
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5850
|
 Myon Verfasst am: 21. Jan 2021 16:27 Titel: Myon Verfasst am: 21. Jan 2021 16:27 Titel: |
 |
|
Der Widerstand ist die Summe der einzelnen Widerstände der beiden Bereiche. Mit der Gleichung aus Wikipedia folgt
)
Das kannst Du noch gleich 25Ohm setzen, um eine Funktion l1(l2) zu erhalten.
Zu b) Statt 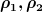 setzt Du nun in der obigen Gleichung die temperaturabhängigen Werte setzt Du nun in der obigen Gleichung die temperaturabhängigen Werte
=\rho_i(T=293\,\mathrm{K})(1+\alpha_i(T-293\,\mathrm{K})))
ein.
Zu c): Wie bist Du auf die Lösungen gekommen, ohne a) und b) zu lösen?
Damit der Widerstand temperaturunabhängig wird, müssen sich die Widerstandsänderungen der beiden Bereiche aufheben, die Funktion f(l1,l2) aus b) muss also gleich null sein. Das ist der Fall, wenn
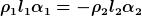
Zusammen mit der ersten Gleichung für den Widerstand bei 20°C hat man damit 2 Gleichungen für die beiden Unbekannten l1, l2. Zur Überprüfung: ich erhalte l1=1cm, l2=3cm - sofern die spez. Widerstände in der Aufgabenstellung die Einheit Ohm*mm haben. |
|
 |
FelixO
Gast
|
 FelixO Verfasst am: 21. Jan 2021 16:46 Titel: FelixO Verfasst am: 21. Jan 2021 16:46 Titel: |
 |
|
Danke! a) und b) habe ich jetzt verstanden.
Bei c)
Stand ja: Temperaturunabhängig. Hab für R(T) = 25 Ohm genommen und das umgestellt nach
l1 = 25 Ohm * A / Rho,1
l2 = 25 Ohm * A / Rho,2
Und dafür die entsprechenden Werte erhalten. Ist dieser Weg falsch? |
|
 |
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5850
|
 Myon Verfasst am: 21. Jan 2021 16:57 Titel: Myon Verfasst am: 21. Jan 2021 16:57 Titel: |
 |
|
| FelixO hat Folgendes geschrieben: | l1 = 25 Ohm * A / Rho,1
l2 = 25 Ohm * A / Rho,2 |
Nur kurz: diese Gleichungen gelten nicht. Es gilt -bei 20°C- die erste Gleichung in meinem vorherigen Beitrag. Nun noch die Gleichung
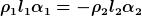
hinzunehmen, und Du hast ein Gleichungssystem mit 2 Gleichungen für die beiden Unbekannten l1, l2. |
|
 |
|
|















