| Autor |
Nachricht |
bloebb
Anmeldungsdatum: 24.07.2017
Beiträge: 139
|
 bloebb Verfasst am: 14. Okt 2017 13:50 Titel: Tensorrechnung, Mannigfaltigkeit, Hyperfläche, Normale bloebb Verfasst am: 14. Okt 2017 13:50 Titel: Tensorrechnung, Mannigfaltigkeit, Hyperfläche, Normale |
 |
|
Hallo!
Ich habe heute leider eine komplizierte Frage. Ich hatte schon mal eine Frage zum gleichen Thema in einem Matheforum gepostet, dort aber keine Antwort bekommen. Zum Glück habe ich selbst meinen Fehler gefunden. Das Thema ist doch etwas kompliziert. Ich versuche jetzt einfach hier mal mein Glück.
Es geht um Tensoren, Mannigfaltigkeit, Hyperflächen und Normalen. Siehe Video https://www.youtube.com/watch?v=c07r4pARzHw Um Normale geht geht es von 1:01:50 bis 1:05:36 Und ich verstehe leider nur Bahnhof.
Mein großes Problem ist, dass ich scheinbar diese "Hyperfläche" nicht verstehe. Im nächsten Videos tauchen wieder derartige Flächen auf, aber dort verstehe ich alles. Aber in diesem Video stehe ich total auf dem Schlauch. Ich kann mir einfach nichts darunter vorstellen. Irgendwie muss es doch einen Zusammenhang geben zwischen einem n-dimensionalen Objekt und irgendwelchen zugehörigen n-1-dimensionalen Hyperflächen, oder?
Auch bekomme ich das einfach nicht auf die Reihe, dass die folgende Formel gelten soll:
_i = (grad \ \lambda)_i = \frac{\partial \lambda}{\partial x^i})
ich habe verstanden, dass der Normalvektor kein Einheitsvektor sein muss. Ich weiß auch, was ein Gradient ist: ein Vektor, der in Richtung der max. Steigung zeigt. Und ich verstehe auch die partielle Ableitung: Ableitung des Skalars (abhängig von Ortskoordinaten) nach den Basisvektoren des Koordinatensystem (hier ein kartesisches Koordinatensystem).
Aber ich verstehe nicht, wie ein Gradient plötzlich zu einem Normalvektor werden kann. Irgendwie wird aus einem Volumen eine Fläche, woraufhin ein ursprünglicher Gradient dann eine Normale auf die Fläche wird???? O.o
Ich bin mir auch nicht sicher, ob ich diese "Niveaufläche" verstanden habe. Soll das eine Ebene sein?
|
|
 |
bloebb
Anmeldungsdatum: 24.07.2017
Beiträge: 139
|
 bloebb Verfasst am: 14. Okt 2017 18:14 Titel: bloebb Verfasst am: 14. Okt 2017 18:14 Titel: |
 |
|
Ich bin vielleicht einen Schritt weitergekommen.
Vielleicht muss man diese Niveau-"Fläche" so ähnlich betrachten wie die Hyper-"Fläche".
Die Hyperfläche muss nicht eine Fläche sein, die kann alles mögliche sein. Nur wenn man von etwas 3dimensionalen ausgeht, erhält man dann eine 2dimensionale Fläche. Geht man aber von etwas 2dimensionalen erhält man ... ähm ... eine Kurve.?
Vielleicht ist das bei der Niveaufläche ähnlich.
Ich habe mir das Beispiel 4 von http://www2.iazd.uni-hannover.de/~erne/Mathematik2/dateien/maple/MB_7_4.pdf angeschaut. Dort ist die Rede von einer Niveau-"Kurve".
Aber die Sache mit dem Gradienten, der die Normale sein soll, ist mir noch immer total schleierhaft. Vielleicht hilft mir das Beispiel 6 weiter. Schaue ich mir aber dann erst morgen oder übermorgen an.
|
|
 |
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5852
|
 Myon Verfasst am: 15. Okt 2017 11:00 Titel: Myon Verfasst am: 15. Okt 2017 11:00 Titel: |
 |
|
Das Skalarprodukt zwischen dem Gradienten und einem Tangentialvektor verschwindet, vgl. die 4. Gleichung auf der 4. Seite im von Dir verlinkten Skript. Allerdings finde ich die Darstellung hier nicht sehr klar, auf Anhieb ist nicht einmal offensichtlich, dass es sich um ein Skalarprodukt handelt.
Dass der Gradient senkrecht auf einer Äquipotentialfläche steht, sieht man sofort, wenn man das vollständige Differential des Potentials bildet, vgl. z.B. in diesem Skript, Gleichung 2.
|
|
 |
bloebb
Anmeldungsdatum: 24.07.2017
Beiträge: 139
|
 bloebb Verfasst am: 15. Okt 2017 15:36 Titel: bloebb Verfasst am: 15. Okt 2017 15:36 Titel: |
 |
|
Ok, ich glaube, langsam verstehe ich es. Allerdings kommt mir da noch etwas seltsam vor.
---------------------------
Ein einfaches Beispiel:
Zuerst mal eine Grafik im Anhang, damit man sich was vorstellen kann.
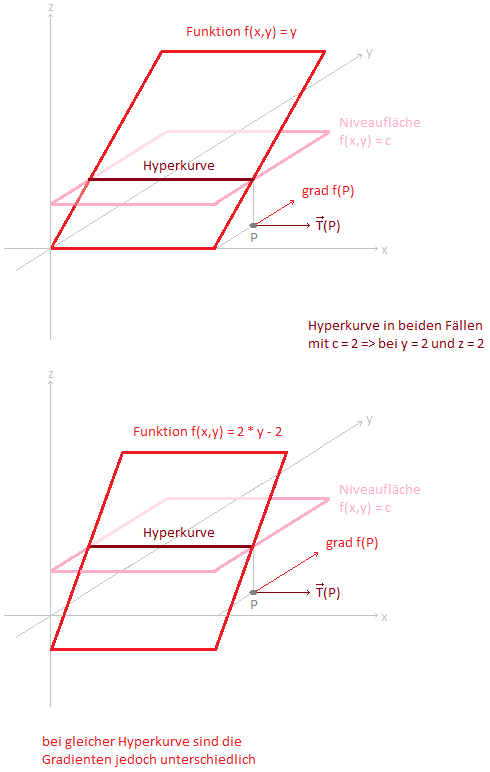
Gegeben ist die Funktion f(x,y) = y
Weiters wähle ich eine Niveaufläche mit f(x,y) = c (ist eine Konstante, z. B. 2)
Schneide ich die Funktion f(x,y) = y mit der Nivaufläche f(x,y) = c, erhalte ich eine Hyperkurve, die in diesem Fall eine Gerade ist.
Die Tangente dieser Gerade zeigt in die Richtung dieser Geraden. Das ist so, als bewege man sich in Richtung dieser Gerade. Der Tangentenvektor zeigt in x-Richtung.
Der Gradient der Funktion f(x,y) = y zeigt in y-Richtung.
Das dot-Produkt von Gradienten- und Tangenten-Vektor ist somit je Punkt auf der Hyperkurve immer 0.
D. h. für einen best. Punkt der Funktion f(x,y) = y steht der Gradient immer normal auf den Punkt der zugehörigen Hyperkurve.
--------------
Jetzt dieses Beispiel ein klein wenig verändert.
Die Funktion soll nun sein: f(x,y) = 2 * y - 2
Die Funktion ist also steiler. Dadurch verändert sich auch der Gradient.
Das seltsame ist nun, dass die Hyperkurve in diesem Beispiel genau so ausschaut wie im vorhergehenden Beispiel, aber der ihr zugedachten Gradienten unterschiedlich sind. Gleiche Gerade, aber unterschiedliche Gradienten.
Das bedeutet dann ja wohl, dass alleine die Richtung des Gradienten eine nützliche Information für die Hyperkurve darstellt, und man den Betrag des Gradienten bei der Betrachtung der Hyperkurve vergessen muss.
Ist das richtig?
| Beschreibung: |
|
| Dateigröße: |
16.63 KB |
| Angeschaut: |
1872 mal |
|
|
|
 |
bloebb
Anmeldungsdatum: 24.07.2017
Beiträge: 139
|
 bloebb Verfasst am: 16. Okt 2017 11:44 Titel: bloebb Verfasst am: 16. Okt 2017 11:44 Titel: |
 |
|
Die Sache mit der Richtung erscheint mir aber auch suspekt.
Ich habe mir 2 Formeln angeschaut, zu denen es im Anhang einige Grafiken gibt. Links sind die Grafiken zur Formel:
sin(x) + 2 * y
und rechts sind die Grafiken zur Formel:
sin(x) - 2 * y
Zuerst sieht man jeweils eine 3D-Grafik, dann eine 2D-Grafik (beide mit freundlicher Unterstützung von wolframalpha.com) und schließlich einen Vektor-Plot der Gradienten (mit freundlicher Unterstützung von desmos.com).
Links zeigen die Gradienten alle irgendwie nach oben, rechts alle irgendwie nach unten. Und das obwohl bei beiden Formeln die Hyperkurve ein Sinus ist.
Dazu braucht man sich nur die jeweils zweite Grafik zu jeder Formel ansehen. Sofern ich die Sache mit den Hyperflächen richtig verstanden habe, ist jede Welle (Sinus) eine mögliche Hyperkurve.
Obwohl beide Hyperkurven gleich sind, zeigen die Gradienten in unterschiedliche Richtungen. Sofern der Gradient der Fläche die Normale der Hyperkurve darstellt, würden also auch die Normalen bei diesen beiden Funktionen in entgegengesetzte Richtungen zeigen.
Also irgendwas ist hier seltsam. Scheinbar verstehe ich diese Materie noch nicht. Könnt ihr mir auf die Sprünge helfen?
| Beschreibung: |
|

Download |
| Dateiname: |
0.png |
| Dateigröße: |
107.64 KB |
| Heruntergeladen: |
237 mal |
|
|
 |
G4mm4G0bl1n
Anmeldungsdatum: 10.05.2017
Beiträge: 93
Wohnort: Darmstadt
|
 G4mm4G0bl1n Verfasst am: 20. Okt 2017 14:28 Titel: G4mm4G0bl1n Verfasst am: 20. Okt 2017 14:28 Titel: |
 |
|
Ich würde es mal hiermit versuchen: https://de.wikipedia.org/wiki/Euklidische_Norm
https://de.wikipedia.org/wiki/Euklidische_Norm#/media/File:Vector-2-Norm_qtl1.svg
Dein Gradiant wird auf die Normebene projeziert. So wie das bei diesem Zylinder & seiner 2 dimensionalen Projektion auch geschieht. Allerdings muss die Koordination der Gradientschnitte mit auf die 2 dimensionale Normfläche projeziert werden. Wozu man das ganze überhaupt macht ist recht einfach. Es dient der Analytik von 3dimensionalen Objekten. Aus der Euklidschen Norm lässt sich z.b auch beweisen das die Volumina eines Zylinders mit dem einer Kugel übereinstimmen, wenn der Radius des Zylinders mit dem Radius einer Kreisfläche der Kugel übereinstimmt.
Da der Satz des Pythagoras gillt, kann entweder Trigonometrisch oder mit der Wurzel gearbeitet werden.
|
|
 |
bloebb
Anmeldungsdatum: 24.07.2017
Beiträge: 139
|
 bloebb Verfasst am: 20. Okt 2017 17:15 Titel: bloebb Verfasst am: 20. Okt 2017 17:15 Titel: |
 |
|
Ich müsste mal ein konkretes Beispiel sehen, wo die erwähnten Hyperflächen, Normflächen, Niveauflächen, weiß-der-Teufel-was-sonst-noch-für-Flächen und zumindest ein Gradient eingezeichnet sind. Dazu noch die Formel und eine zum Gradienten zugehörige Normale, und schon bin ich glücklich.

Kennst du zufällig so eine Grafik?
Was meinst du eigentlich mit "Normfläche"? Ist das die vom Prof erwähnte Niveaufläche? Ist das die virtuelle Ebene, mit der der Kegel geschnitten wird, und aufgrund dessen sich der blaue Kreis am Kegel ergibt? Also nicht der untere blaue Kreis auf der Ebene, sondern der obere blaue Kreis am Kegel?
Was sagst du eigentlich zu meinen Einträgen und Grafiken? Was davon stimmt, was nicht?
|
|
 |
|
|

















