| Autor |
Nachricht |
eva1
Anmeldungsdatum: 06.10.2010
Beiträge: 532
|
 eva1 Verfasst am: 23. Okt 2012 18:49 Titel: Wasserstoffatom im zeitabhaengigen Magnetfeld |
 |
|
Hi Leute,
ich hab ein Problem.
Gegeben sei ein Wasserstoffatom im Zustand:
d.h. glaub n=1 , l=1 , ml = 0 , ms=1/2
Nun wird ein Magnetfeld eingeschaltet, was folgenden Hamiltonian hat:
 \left(\hat L_x + 2 \hat S_x\right))
Nun sollen die moeglichen Endzustaende bestimmt werden.
Jetzt hab ich nicht so wirklich viel Ahnung was ich tun soll. Mein erster Gedanke war die Schroedingergleichung zu loesen, aber diesen habe ich schnell wieder verforgen, da ich ja noch den alten Hamiltonian habe. Muss man das mit ueberlegen loesen oder mit rechnen.
Habt ihr eine Idee?
Viele Gruesse,
eva  |
|
 |
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18027
|
|
|
eva1
Anmeldungsdatum: 06.10.2010
Beiträge: 532
|
| eva1 Verfasst am: 23. Okt 2012 19:00 Titel: |
|
|
Mhm, das wuerde mir etwas komisch vorkommen, da wir in diesem Kurs keine zeitabhaengige Stoerungstheorie gemacht haben.
Sonst noch welche Ideen? |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18027
|
| TomS Verfasst am: 23. Okt 2012 19:16 Titel: |
|
|
Na, du kannst den kompletten Hamiltonian als H=H°+H' schreiben und versuchen zu lösen, aber das wäre komisch und ggf. schwierig.
Aber wenn das steht "Nun sollen die moeglichen Endzustaende bestimmt werden" dann sehe ich nur die zwei Möglichkeiten.
Andere Methoden?
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
eva1
Anmeldungsdatum: 06.10.2010
Beiträge: 532
|
| eva1 Verfasst am: 23. Okt 2012 19:24 Titel: |
|
|
Die Aufgabenstellung ist auf Englisch, vll. hab ich auch etwas falsch verstanden, ich kanns ja mal hier hereinstellen.
"A hydrogen atom in state |1,1,0,1/2> is subjected to a time-dependent magnetic field  \boldsymbol{e_x} ) . Neglecting terms quadratic in the magnetic field, the interaction between the electron and the external magnetic field, B , is described by the Hamiltonian:
 \boldsymbol{B})
Determine the possible final states.
Vielleicht ist die Aufgabe nur verstehentlich auf den Uebungszettel. Koennte ja sein.
Danke schon mal fuer deine Hilfe.  |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18027
|
| TomS Verfasst am: 23. Okt 2012 22:47 Titel: |
|
|
Wir schreiben mal den Hamiltonian auf:
 \vec{B} = H_0 + \frac{\mu_B\,B_0}{\hbar} \,\sin\omega t\,\left(L_x+ 2 S_x\right) )
Dann schreiben die x-Komponente von Bahndrehimpuls und Spin mittels der Leiteroperatoren um
 )
Nun betrachten wir den Zeitentwicklungsoperator
 = e^{-iH(t-t_0)/\hbar} = \sum_{n=0}^\infty \frac{(-i)^n(t-t_0)^n}{n!\,\hbar^n}H^n)
Jetzt würde ich mal den o.g. Hamiltonoperator H auf den genannten Zustand anwenden. Der Zustand ist dabei ein Eigenzustand zum ungestörten Hamiltonoperator. Die Störung H' wirkt nur über die Leiteroperatoren, d.h. du musst dir überlegen, wie diese Terme auf die Zustände wirken
|1,1,0,1/2\rangle )
|1,1,0,1/2\rangle )
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
eva1
Anmeldungsdatum: 06.10.2010
Beiträge: 532
|
| eva1 Verfasst am: 23. Okt 2012 22:54 Titel: |
|
|
Hab ich mir auch schon ueberlegt, aber ich dachte der Zeitentwicklungsoperator gilt nur fuer zeitunabhaengige Hamiltonians, oder?
Daher dachte ich, dass man die Schroedinger-EQ loesen muss. |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18027
|
| TomS Verfasst am: 23. Okt 2012 23:42 Titel: |
|
|
Puh, ja, das ist ein Punkt den ich übersehen habe.
Man kann das lösen, und zwar über die (zunächst nur formale) Dyson-Reihe
 = \text{T}\,\text{exp} \left[ -\frac{i}{\hbar}\int_{t_0}^tdt\,H(t) \right])
Dabei treten Integrale der Form
\,H(t_2)\,\ldots\,H(t_{i+1})\,\ldots)
auf. Die Struktur des (iterierten) Drehimpulsterms und damit die Wirkung auf den ungestörten Eigenzustand bleibt dabei unverändert. D.h. die Schlussfolgerung bzgl. der erreichbaren Endzustände bleibt gültig.
Aber das bedeutet mit Kanonen auf Spatzen schießen!
Außerdem sind die Gleichungen und insbs. die Integrale nicht wohldefiniert, wenn man eine oder beiden Zeiten gegen unendlich gehen lässt. Das ändert wieder nichts an der algebraischen Struktur, aber unschön ist es trotzem.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18027
|
| TomS Verfasst am: 24. Okt 2012 00:02 Titel: |
|
|
| eva1 hat Folgendes geschrieben: | | "A hydrogen atom in state |1,1,0,1/2> is subjected to a time-dependent magnetic field ... Neglecting terms quadratic in the magnetic field, the interaction between the electron and the external magnetic field, B , is described by ... Determine the possible final states. |
Zunächst nochmal eine generelle Feststellung: der Hamiltonoperator H' wirkt nicht auf n und l, d.h. zunächst mal können nur folgende Terme entstehen
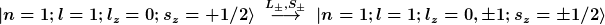
Dann könnte man auch auf die Idee kommen, dass | eva1 hat Folgendes geschrieben: | | "Neglecting terms quadratic in the magnetic field ... |
auch bedeuten könnte, man solle generell nur Terme bis zur ersten Ordnung in H' betrachten (käme mir aber komisch vor). Wenn dem so wäre, dann wäre man mit dem Hinschreiben der Schrödingergleichung praktisch schon fertig; alle o.g. Terme in B² fallen weg und man muss jeweils nur den ersten Term auswerten (das ist aber zunächst keine vernünftige Näherung sondern ein sehr eingeschränkte Interpretation der Aufgabenstellung, da für kleine B aber dafür genügend große t diese Näherung nicht mehr gelten muss.
Hast du mal einen allgemeinen = exakten Ansatz versucht? Könnte es sein, dass man das Problem exakt lösen kann?
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
jh8979
Moderator
Anmeldungsdatum: 10.07.2012
Beiträge: 8576
|
| jh8979 Verfasst am: 24. Okt 2012 01:14 Titel: |
|
|
| TomS hat Folgendes geschrieben: |
... zunächst mal können nur folgende Terme entstehen
|
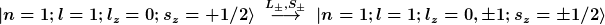
Ich glaub mehr war gar nicht gefragt in der Aufgabe. Es ging nur um die moeglichen Endzustaende, keine Uebergangswahrscheinlichkeiten oder so ... |
|
|
eva1
Anmeldungsdatum: 06.10.2010
Beiträge: 532
|
| eva1 Verfasst am: 24. Okt 2012 11:45 Titel: |
|
|
Also sind die moeglichen Endzustaende:
L+ :
L- :
S-:
S+ geht nicht, da ja schon m_s=1/2 .
Aber warum ist das so? Nur weil ich den Hamilton auf den Anfangszustand anwende bekomme ich doch nicht die Endzustaende? |
|
|
|
Registrieren
Login
FAQ
Suchen
