| Autor |
Nachricht |
Ultima
Anmeldungsdatum: 15.04.2005
Beiträge: 151
|
 Ultima Verfasst am: 19. Nov 2008 16:21 Titel: Feldstärketensor und Invariante Ultima Verfasst am: 19. Nov 2008 16:21 Titel: Feldstärketensor und Invariante |
 |
|
Guten Abend,
es sei 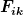 der bekannte Feldstärketensor, z.b. hier zu finden, http://de.wikipedia.org/wiki/Elektromagnetischer_Feldst%C3%A4rketensor der bekannte Feldstärketensor, z.b. hier zu finden, http://de.wikipedia.org/wiki/Elektromagnetischer_Feldst%C3%A4rketensor
und der dazu duale Feldstärketensor  gegeben. gegeben.
(wobei in der mir vorliegenden Version die Komponenten des elektr. Feldes nicht durch die Lichtgeschwindigkeit c geteilt wurden. Für mein Problem sollte das aber keine Probleme bereiten.)
Es gilt zu zeigen: 
Mein Problem ist jetzt einfach, dass ich nicht weiß wie man das Skalarprodukt dieser Tensoren bildet. Bei diesen Tensoren handelt es sich ja an und für sich um Matrizen. Wir haben bisher aber nur das Skalarprodukt für Vierervektoren eingeführt und es folgendermaßen definiert:

Aber wie funktioniert das bei obigen Tensor? vielen Dank schonmal. |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 19. Nov 2008 19:30 Titel: dermarkus Verfasst am: 19. Nov 2008 19:30 Titel: |
 |
|
Analog wie bei Vektoren: Die jeweiligen Matrixelemente paarweise multiplizieren und das dann addieren.
Magst du mal den oben genannten dualen Feldstärkevektor aufschreiben? Klappt es dann schon? |
|
 |
Ultima
Anmeldungsdatum: 15.04.2005
Beiträge: 151
|
 Ultima Verfasst am: 19. Nov 2008 22:31 Titel: Ultima Verfasst am: 19. Nov 2008 22:31 Titel: |
 |
|
Ja gerne, also der duale Feldstärkevektor lautet bei uns:

Der "normale" Feldstärketensor lautet so:

Von den beiden Tensoren soll ich jetzt das Skalarprodukt berechnen und mir ist nicht klar, nach welchen Kriterien man die Vorzeichen richtig setzt. Klar weiß ich was heraus kommt, dass soll ich ja gerade zeigen, aber ich würde es gerne auch verstehen.
Wenn man nämlich die erste Zeile vom dualen Feldstärkevektor mit der ersten Spalte des Feldstärkevektors multipliziert stimmen ja die Vorzeichen nicht mehr. Es kommt ja alles mit Plus, richtig wäre aber alles mit Minus als Vorzeichen.
Kannst du mir das erklären? |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 19. Nov 2008 22:51 Titel: dermarkus Verfasst am: 19. Nov 2008 22:51 Titel: |
 |
|
| Ultima hat Folgendes geschrieben: | Ja gerne, also der duale Feldstärkevektor lautet bei uns:

|
Kann es sein, dass du rechts unten (4-3 und 3-4 - Komponente) noch die Vorzeichen vertauscht hast? Wie bekommst du den dualen Tensor aus dem "normalen"?
| Zitat: |
Wenn man nämlich die erste Zeile vom dualen Feldstärkevektor mit der ersten Spalte des Feldstärkevektors multipliziert
|
Ah, Vorsicht, das wäre die normale Matrizenmultiplikation. Dafür müsste man die Indices unten anders schreiben (a la A_ij * A_jk).
Was hier steht, ist eine "Kontraktion zweier Tensoren auf einen Skalar", da multipliziert man nicht Zeile mit Spalte, sondern jeweils immer die Matrixelemente miteinander, die genau an derselben Stelle in ihrer Matrix stehen.
| Zitat: |
Von den beiden Tensoren soll ich jetzt das Skalarprodukt berechnen und mir ist nicht klar, nach welchen Kriterien man die Vorzeichen richtig setzt.
|
Ach, du denkst da zum Beispiel an so etwas wie einen metrischen Tensor, wie du ihn von den Vektoren her kennst? Ich glaube nicht, dass man hier für die zweidimensionalen Matrizen so etwas braucht; wenn ich das ohne so etwas rechne, komme ich auf das Ergebnis der Aufgabenstellung. |
|
 |
Ultima
Anmeldungsdatum: 15.04.2005
Beiträge: 151
|
 Ultima Verfasst am: 20. Nov 2008 08:27 Titel: Ultima Verfasst am: 20. Nov 2008 08:27 Titel: |
 |
|
Naja dann war das einfach mein Fehler, dass ich die normale Matrizenmultiplikation immer machen wollte. Wir haben den dualen Tensor duch Multiplikation mit dem total antisymmetrischen Tensor  bekommen. Laut meiner Vorlage stimmen die Vorzeichen, aber vielleicht hat sich jemand verschrieben. bekommen. Laut meiner Vorlage stimmen die Vorzeichen, aber vielleicht hat sich jemand verschrieben.
Ansonsten haben wir tatsächlich das Skalarprodukt dadurch definiert, dass wir einen metrischen Tensor eingeführt haben, dessen Diagonalelemente 1, -1,-1,-1 sind, so komme ich auch auf die Definiton von oben. Bei Tensoren war mir das allerdings nicht klar. Wir haben bspw. aus dem Tensor 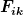 den Tensor den Tensor  bestimmt, indem man zweimal den metrischen Tensor vorne herand multipliziert hat, also so: bestimmt, indem man zweimal den metrischen Tensor vorne herand multipliziert hat, also so:

Ich dachte jetzt, dass kann ich bei dieser Aufgaben ebenfalls verwenden. |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 20. Nov 2008 10:24 Titel: dermarkus Verfasst am: 20. Nov 2008 10:24 Titel: |
 |
|
| Zitat: |
Wir haben bspw. aus dem Tensor 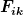 den Tensor den Tensor  bestimmt, indem man zweimal den metrischen Tensor vorne herand multipliziert hat, also so: bestimmt, indem man zweimal den metrischen Tensor vorne herand multipliziert hat, also so:

|
Ach so, das brauchst du nur, wenn die Indices noch bei beiden Tensoren unten stehen. Wenn du bereits die Tensoren in der Form dastehen hast, dass beim einen Tensor die beiden Indices oben stehen und beim anderen unten, dann ist die "Arbeit mit den metrischen Tensoren schon getan", und man kann direkt die Vorzeichen, die drinstehen, fürs Rechnen nehmen.
| Ultima hat Folgendes geschrieben: | Wir haben den dualen Tensor duch Multiplikation mit dem total antisymmetrischen Tensor  bekommen. Laut meiner Vorlage stimmen die Vorzeichen, aber vielleicht hat sich jemand verschrieben. bekommen. Laut meiner Vorlage stimmen die Vorzeichen, aber vielleicht hat sich jemand verschrieben.
|
Dann könntest du ja, wenn du magst, das mal nachrechnen, um das zu kontrollieren. Habt ihr das direkt in der Schreibweise mit den Indices aufgeschrieben und gerechnet? Wie sieht damit die komplette Gleichung für die Matrixmultiplikation aus, mit der du den dualen Tensor bekommst
(Kann es übrigens sein, dass ihr die Bezeichnung des total antisymmetrischen Tensors als  geschrieben habt und nicht als geschrieben habt und nicht als  ?) ?) |
|
 |
Ultima
Anmeldungsdatum: 15.04.2005
Beiträge: 151
|
 Ultima Verfasst am: 20. Nov 2008 19:58 Titel: Ultima Verfasst am: 20. Nov 2008 19:58 Titel: |
 |
|
Hi,
bei uns heißt der totale antisymmetrische Tensor wirklich  , der steht sogar so im Landau drinnen. Das nachrechnen könnte ich wirklich mal probieren und dann habe ich den dualen Tensor nochmals selbst bestimmt. Rein theoretisch wird das Vorzeichen wohl falsch sein. , der steht sogar so im Landau drinnen. Das nachrechnen könnte ich wirklich mal probieren und dann habe ich den dualen Tensor nochmals selbst bestimmt. Rein theoretisch wird das Vorzeichen wohl falsch sein.
Aber kann ich mir nun allg. merken, dass ich einfach die Tensoren komponentenweise multipliziere und dann aufaddiere um das Skalarprodukt zu berechnen? Kannst du mir vielleicht sagen, wo ich diese Aussage finde, denn ich soll das ja nachrechnen, dass die obige Aussage stimmt und dann wäre die Aufgabe ja doch sehr sehr einfach. |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 20. Nov 2008 20:08 Titel: dermarkus Verfasst am: 20. Nov 2008 20:08 Titel: |
 |
|
| Ultima hat Folgendes geschrieben: | | Kannst du mir vielleicht sagen, wo ich diese Aussage finde, |
Na, diese Aussage steht ja direkt in der Schreibweise mit den Indices schon drin: Weil das bei jedem der beiden Tensoren dieselben Indices in derselben Reihenfolge (ik) sind, muss man natürlich dementsprechend auch immer jeweils dieselben Tensorelemente miteinander multiplizieren. |
|
 |
Ultima
Anmeldungsdatum: 15.04.2005
Beiträge: 151
|
 Ultima Verfasst am: 21. Nov 2008 10:49 Titel: Ultima Verfasst am: 21. Nov 2008 10:49 Titel: |
 |
|
Achso, jetzt habe ich es verstanden. Und warum kann ich in diesem Fall hier unbekümmert alles aufaddieren und im anderen Fall, also z.b. bei
 bekomme ich ja die räumlichen Komponenten immer mit - und nur die erste Komponente mit plus. Das liegt ja eben daran weil ich diesen metrischen Tensor verwende um die Indices beide unten zu haben. Müsste so stimmten was ich sage, oder? bekomme ich ja die räumlichen Komponenten immer mit - und nur die erste Komponente mit plus. Das liegt ja eben daran weil ich diesen metrischen Tensor verwende um die Indices beide unten zu haben. Müsste so stimmten was ich sage, oder? |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 21. Nov 2008 11:49 Titel: dermarkus Verfasst am: 21. Nov 2008 11:49 Titel: |
 |
|
Damit bin ich noch nicht ganz einverstanden. Ich versuchs mal umgangssprachlich zu formulieren:
Wenn die Indices beim einen oben stehen und beim anderen unten, dann kannst du "unbekümmert drauflosmultiplizieren" und das Skalarprodukt bilden. Denn dann sind die Vektoren bzw. Tensoren "bereit dafür".
Wenn die Indices aber zum Beispiel noch bei beiden unten stehen, dann muss man erst beim einen von beiden den Index bzw. die Indices mit dem metrischen Tensor "hochziehen", damit die beiden Vektoren bzw. Tensoren bereit für das Bilden des Skalarproduktes sind.
Formal und präziser formuliert würde man das mit Begriffen wie kovarianter und kontravarianter Vektor, ... sagen. Habt ihr so etwas schon genau in der Vorlesung gehabt und in Übungen geübt?
Habt ihr da zum Beispiel auch etwas gesagt wie:
"Damit man aus zwei Vektoren das Skalarprodukt bilden kann, muss, wenn man streng den Regeln für Matrizenmultiplikation folgen möchte, strenggenommen der linke Vektor ein Zeilenvektor und der rechte Vektor ein Spaltenvektor sein. Der Unterschied zwischen kovariantem und kovariantem Vektor ist wie so ein Unterschied zwischen Zeilen- und Spaltenvektor." ? |
|
 |
Ultima
Anmeldungsdatum: 15.04.2005
Beiträge: 151
|
 Ultima Verfasst am: 21. Nov 2008 12:32 Titel: Ultima Verfasst am: 21. Nov 2008 12:32 Titel: |
 |
|
Hi Markus,
also wir haben in der Vorlesung bereits die Begriffe kontravariante und kovariante Vektoren drangenommen. Bei diesen Begriffen geht es ja um das Transformationsverhalten von Vektoren. Deshalb sind mir die Begriffe noch nicht ganz klar, wenn man z.b. einen Vierervektor hat, dann ändert sich in der räumlichen Komponente das Vorzeichen, um von einem ko- zu einem kontravarianten Vektor zu kommen nicht wahr?
Ich habe leider gerade nicht mein Skript zur Hand und kann genaueres dazu erst morgen schreiben.
Ich versehe dich so:
 : hier kann man sofort das Skalarprodukt berechnen : hier kann man sofort das Skalarprodukt berechnen
 : hier kann man es nicht berechnen sondern macht folgendes: : hier kann man es nicht berechnen sondern macht folgendes:  jetzt ist man in der Lage das Skalarprodukt zu berechnen. Der metrische Tensor sorgt gerade dafür, dass ein Vierervektor der Form jetzt ist man in der Lage das Skalarprodukt zu berechnen. Der metrische Tensor sorgt gerade dafür, dass ein Vierervektor der Form ) : zu : zu ) wird. Da bin ich jetzt dahinter gekommen. Deshalb ist es dann auch klar, woher das minus vor den räumlichen Komponenten im Skalarprodukt kommt. wird. Da bin ich jetzt dahinter gekommen. Deshalb ist es dann auch klar, woher das minus vor den räumlichen Komponenten im Skalarprodukt kommt.
Bleibt nur noch die Frage, nach den neuen Begriffen Kovariant und Kontravariant. |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 21. Nov 2008 12:44 Titel: dermarkus Verfasst am: 21. Nov 2008 12:44 Titel: |
 |
|
Noch nicht ganz. Da hilft dir wahrscheinlich auch ein gründlicher Blick das entsprechende Kapitel in deinem Skript oder dem Rela-Buch weiter. Was findest du da zu Stichworten wie Lorentz-Skalar?
| Ultima hat Folgendes geschrieben: |
 : hier kann man sofort das Skalarprodukt berechnen : hier kann man sofort das Skalarprodukt berechnen
|
Einverstanden 
| Ultima hat Folgendes geschrieben: | sondern macht folgendes:  |
So würde ich das nicht sagen. Eher so:
| Zitat: |

|
ist kein Skalarprodukt.
Aber

ist ein Skalarprodukt. |
|
 |
Ultima
Anmeldungsdatum: 15.04.2005
Beiträge: 151
|
 Ultima Verfasst am: 21. Nov 2008 12:57 Titel: Ultima Verfasst am: 21. Nov 2008 12:57 Titel: |
 |
|
Ok, so habe ich es an und für sich auch gemeint. Das "=" war natürlich Quatsch.
Mein Skript und der Landau unterscheiden sich nicht wirklich  Ich finde die Vorlesung aber top und die Aufgaben machen auch Spaß. Ich finde die Vorlesung aber top und die Aufgaben machen auch Spaß. |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 21. Nov 2008 13:14 Titel: dermarkus Verfasst am: 21. Nov 2008 13:14 Titel: |
 |
|
| Ultima hat Folgendes geschrieben: | Das "=" war natürlich Quatsch.
|
Das Gleichheitszeichen in  war vollkommen richtig. Nur hat diese Gleichung nichts mit dem zu tun, was man macht, wenn man den Lorentzskalar aus zwei kovarianten Vektoren bilden möchte. war vollkommen richtig. Nur hat diese Gleichung nichts mit dem zu tun, was man macht, wenn man den Lorentzskalar aus zwei kovarianten Vektoren bilden möchte.
| Zitat: |
Ich finde die Vorlesung aber top und die Aufgaben machen auch Spaß. |
Schön zu hören 
Welchen Landau meinst du da? Den Landau-Lifschitz-Band zur Relativitätstheorie oder ein anderes Buch von Landau über Relativitätstheorie? |
|
 |
Ultima
Anmeldungsdatum: 15.04.2005
Beiträge: 151
|
 Ultima Verfasst am: 22. Nov 2008 23:10 Titel: Ultima Verfasst am: 22. Nov 2008 23:10 Titel: |
 |
|
Hi,
ich lese den Landau-Liftschitz Band 2 Klassische Feldtheorie. Ließt sich ganz gut und kann ihn empfehlen. Ist denke ich mal anders aufgebaut als gewöhnliche Lehrbücher wie der Nölting oder für Exphysik der Demtröder. Ist jedenfalls nicht so trocken wie ich finde und gut verständlich. Habe aber auch schon gehört, dass er einigen zu schwer zu lesen ist.
Bist / Warst du auch ein Landau-Lifschitz Leser?
Gruß |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 04. Dez 2008 00:54 Titel: dermarkus Verfasst am: 04. Dez 2008 00:54 Titel: |
 |
|
Mit dem Landau-Lifschitz habe ich bisher noch nicht wirklich gearbeitet.
Ich habe nun mal ein bisschen in den 2. Band davon hineingeschaut; die Kapitel über spezielle Relativitätstheorie scheinen mir darin tatsächlich relativ verständlich und gut lesbar geschrieben zu sein. (Nur an einigen Stellen verwendet er ein bisschen mehr Formalismus als nötig (z.B. Langrangefunktion, Prinzip der kleinsten Wirkung)).
Wenn du an manchen Stellen merken solltest, dass du allein mit dem einen Buch noch nicht so richtig konkret und anschaulich verstanden hast, wie man etwas mal konkret rechnet, dann kann es sein, dass es sehr hilfreich ist, auch andere Bücher zur speziellen Relativitätstheorie mit zum Arbeiten zu verwenden. Das müssen gar nicht mal dicke Schmöker sein, oft sind "kleine, aber feine" Bücher wie zum Beispiel das von Ruder zur speziellen Relativitätstheorie
http://www.amazon.de/Vieweg-Studium-Nr-66-Spezielle-Relativit%C3%A4tstheorie/dp/3528072660
sogar noch viel besser fürs unmittelbare Verständnis.  |
|
 |
|

















 Ich finde die Vorlesung aber top und die Aufgaben machen auch Spaß.
Ich finde die Vorlesung aber top und die Aufgaben machen auch Spaß.